基于小波分析的时间序列事件检测方法

卢北辰，常子星，金 涛，王建民

(清华大学 软件学院，北京 100084)

0 引言

随着信息技术的快速发展，人们发现问题、描述问题、解决问题的思路较以往有了很大区别，基于信息化、智能化的方法逐渐取代了传统的基于经验和人工的方法，成为人们对现实系统进行观测、分析和优化的主要手段。在许多情况下，这一任务通过时间序列数据的形式，对现实世界的物理系统进行表征和观测，在此基础上，结合过程挖掘的手段，对系统的状态(state)和运行情况进行建模和优化，进而发现和解决系统中存在的问题。

时间序列(time series)指按时间顺序获得的一系列有序观测值，是对物理世界的待观测系统进行描述和分析的重要手段和表现形式，在物联网、计量经济学、生物医学分析、气象研究及恶劣天气预测等领域均有广泛的应用。随着物联网(Internet of Things, IoT)技术的发展和传感器监控系统的应用，日志规模和数据维度均不断增长，采用事件(event)的概念对时间序列进行挖掘和抽象具有重要意义。事件是过程挖掘中的一个重要概念，记录了一个活动的基本属性及其发生的时间戳。对事件日志进行分析挖掘既可以发现一个业务过程，也可以将事件日志与已知过程模型进行比较来检验其合规性，或者利用实际业务过程中产生的事件日志来扩展或改进现有的过程模型[1]。

目前，事件日志的来源主要依赖于一个完善信息系统对预先规定好的事件的记录，而在实际生产中，某些工业系统只是单纯地记录传感器的时间序列，并不会生成可用的事件日志；另一方面，日志所记录的事件是有限的，一些不在系统设计者意料之中的事件并不能被有效记录下来。因此，对时间序列进行事件检测是过程挖掘的重要任务之一。

1 相关工作

从时间序列中检测事件的方法很多，本文基于现有工作[2]，采用两次抽象的方法完成时间序列数据事件发现的工作。

第1阶段抽象过程称为状态划分，按一定规则将时间序列划分为不同的区间，相同标签区间内的数据具有简单且相似的模式，将这种模式称为数据的一个状态，将只包含数据一种状态的时间区间称为状态区间；第2阶段抽象过程称为事件检测，划分状态区间后，将状态区间按照一定模式组装起来，获得一个更复杂的数据模式，这种模式称为时间模式(temporal pattern)，频繁的时间模式被认为是一个可能的事件。

1.1 状态划分

状态划分可使后续工作在更加抽象的级别上展开，用一个特定的标签表示这一组子序列的特征[3]能够大大降低数据的规模和维数，使后续计算更加简单高效。相比于机器学习聚类的方式[4]，通过状态组装的事件更加直观，具有更强的可解释性。对于为子序列赋予特征标签的问题，目前主要有基于归纳导出和基于演绎导出两种解决方法。

1.1.1 归纳导出方法

通过归纳的方法从原始的时间序列导出一组标签，采用该标签划分状态区间。为了划分数据，常采用基于相似度判定的聚类方法，该方法将时间序列的一个子序列视为一个数据对象，划分后的每个簇视为一个拥有相同标签的子序列集合[5]。

1.1.2 演绎导出方法

归纳方法可以得到细致划分的时间序列，对得到的每个簇的形状都有精准的描述。缺点是在很多情况下计算量过于庞大，限制了其应用范围。因此，本文使用的方法不再试图对曲线的形态进行精准描述，而是用一个枚举标签标记事件序列的每一个小段。例如，对一个区间的形状描述仅限于增或减；也可以稍微深入一点，区分凸函数和凹函数。函数近似方法和平滑方法均可用于划分区间，每个区间被视为一个状态。

1.2 事件检测

前述的状态是时间序列的第1阶段抽象，也是人类能感知到的最小层次，如空气里的温度上升状态、高湿度状态都可以被人的感官感知到。然而，通常人类所理解的是更高级更复杂的事件，一个事件往往对应很多个状态改变的组合，为了描述事件或分析该事件的影响，需要将所有相关状态组合起来，以状态组合的变化表示一个特定的事件[6]。因此，需要采用算法进行事件层次的第2阶段抽象。

1.2.1 基于一致的时态语法

基于一致的时态语法(Unification-based Temporal Grammar, UTG)[7]是一种规则语言，用来描述多元时间序列数据，其用一阶逻辑提供时序概念的层次描述。序列是从相似的相邻状态中衍生出来的，当两个或两个以上的状态同时发生时，认为它们形成一个事件。当原始的时间序列存在缺失导致数据不连续时，UTG方法会检测出两个事件而不是将其合并，这样不利于多元数据的处理。

1.2.2 时间模式识别方法

时间模式指几个状态特定位置关系的组合[2]。时间模式识别方法通过对时间模式进行形式化定义，采用滑动窗口的方式寻找区间序列里出现最频繁的几个时间模式。该方法认为，一个时间模式出现得越频繁，越有研究价值，该时间模式更可能对应一个真实的事件。本文用此法作为第2阶段抽象的方法。

2 算法介绍

2.1 采用演绎导出方法划分状态

算法的主要思想是预先使用平滑技术消除原始数据噪声，然后根据平滑后的数据提取形状特征。对于一个有意义的平滑方法，t时刻的估计值应该与t时刻附近的观测值有关，而且根据观测值所在的时刻与t时刻的距离，其权重也需进行相应调整。核函数k(u)用于描述这一权重分布的函数，常用的核函数有一次核函数、二次核函数、高斯核函数等，其应满足质量分布集中在0附近，当|u|≥1时，k(u)会迅速衰减或完全消失。用带宽参数s控制核函数的平滑程度，有

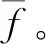
在原始信号为离散的情况下，有

根据上述方法计算一个序列的标签，进而将原始的时间序列数据划分为不同的状态区间，并为其赋予不同的标签，从而完成对时间序列的第一级抽象。下面给出其形式化定义：

定义1状态区间序列。给定一个非空区间序列{[bi,fi]}，每个区间包含一个标签si∈S，三元组(b,f,s)称为状态区间。如果满足∀(bi,fi,si),(bj,fj,sj)，有bj≤fi≤fj⟹si≠sj，则称{(bi,fi,si)}=(b1,f1,s1),(b2,f2,s2),(b3,f3,s3),…是S上的一个状态区间序列。

定义1要求该序列中的区间是尽可能扩张的。然而，值得关注的是，该定义既不要求这些区间之间互不重叠，也不要求对序列的划分是完全的，相邻两个区间之间可以部分重叠，也可以存在间隙。因此，在此定义下，不需要区分单变量分析和多变量分析的情况，或者说算法本身就具备处理多维数据的能力。

2.2 频繁时间模式发现

2.2.1 概念定义

定义了状态区间序列后，进一步考虑区间之间的关系。对区间之间关系的描述来源于从现有工作得到的启发[8]，将两个区间之间的时间关系划分为13种，如表1所示，将这些位置关系组成的集合记为I。

给定任意n个状态区间(bi,fi,si)，其中1≤i≤n，这n个区间的相对位置关系可以由一个n×n的矩阵R描述。矩阵R第i行第j列的值R[i,j]描述第i个区间和第j个区间的位置关系，取值为上述13种之一。

表1 区间A与B的位置关系及其符号表示

令S={(bi,fi,si)}表示状态区间的集合。(bi,fi,si)表示si在区间[bi,fi]中成立，则该三元组描述了一个变量在一段时间内的状态，该状态被视为对应区间的标签。由此，给出时间模式的定义：

定义2时间模式。称二元组P=(L,R)为一个n×n的时间模式，其中L=(l1,l2,…,ln)为一个标签序列，R∈In×n为n个区间之间相对位置关系的描述矩阵。

显然，在一个区间序列中，可能存在很多不同的子序列可以映射到同一个时间模式上。对于一个状态区间序列{(bi,fi,si),1≤i≤n}和时间模式(L,R)，如果∀i,j,1≤i,j≤n，有si=li且ir([bi,fi],[bj,fj])=R[i,j]，则称该状态区间序列是该时间模式的一个实例，其中ir指internal relation，表示两个区间的位置关系。

2.2.2 算法描述

根据上述定义，时间模式可以是任意几个状态区间的位置组合。对于一个大小为n的状态集S，可能存在的时间模式种类为n的指数级，只需考虑那些出现频率更高的时间模式。因此，需要检测给定的时间模式在状态区间序列中出现的频率。

算法1子关系检测。

func subsection_ check(P,Q,π)

if dim(P)>dim(Q) then

return false

end if

π(·)←0;

return perm(1,1,P,Q,π)

func perm(i,j,P,Q,π)

found=false

repeat

if sP(i)=sQ(i) then

π(i)=j;ok=true

for k=1 to i do

ok=ok and RP[i,k]=RQ[j,π[k]]

end for

if ok then

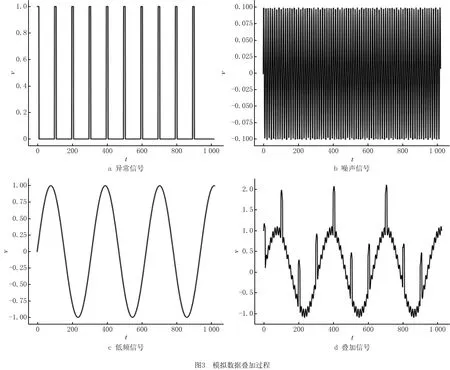
if i

found=perm(i+1,j+1,P,Q,π)

end if

end if

end if

j=j+1

until(j>dim(Q)) or (found)

return found

算法1给出了子关系检测方法。对于两个模式P和Q，该算法可以检测出P是否为Q的子模式。其中，子模式的定义为，若对于模式Q，通过删除Q中的一些状态s及其位置关系可以得到模式P，则P是Q的子模式。

如图1所示，通过该算法可以检测一个待测模式P是否位于时间序列上指定位置的窗口中。沿时间轴滑动该窗口，即可计算出模式P在全区间序列中出现的次数，从而获得最频繁出现的模式。

对于任意k频繁模式，其包含的(k-1)阶子模式也应该是频繁的。因此，从k=0开始计算，每次只保留频繁的模式，向上即可递推出k阶频繁模式。改进后的算法如算法2所示。

算法2频繁模式检测。

func find_freq_patterns(S,(Ii)i,(Fi)i)

k=1

Ck={sinS}

repeat

suppor_ estimation(Ck,(Ii)i)

Fk=P∈Cx|supp(P)> suppmin

Ck+1=candidata_ generation(Fk)

k=k+1

until Ck=∅

3 优化方案

3.1 演绎导出方法优化

基础的演绎导出方法存在一些问题，即平滑不仅能消除噪声，也会在一定程度上消除时间序列的原始特征。另一方面，即使不考虑随噪声被消除的高频信号特征，低频信号的极值点位置也会随平滑过程发生一定偏移。

一个典型的时间序列往往受各种来源信号分量的影响，每段信号都有可能是一些在时域和频域上有不同行为特征的组合。在这种复杂的情况下，一般的平滑方法很难选择一个合适的核函数f(u)和带宽参数s，也无法将组合在一起的不同频率的信号分量拆分开来。本文应用基于小波分析(wavelet analysis)的多尺度分析方法，分别在不同尺度中对信号进行分析，将存在于不同频域中的信号区分开来。

3.1.1 小波分析

小波分析是一种信号分析技术，用于描述信号中的局部现象。

与平滑方法的核函数类似，小波分析中也可以通过参数s和u调整母小波(mother wavelet)的尺度和位置，从而得到一系列函数。具体而言，将母小波函数ψ(t)进行时间位移u后，再用尺度因子s进行放缩，即可得到小波函数

将小波函数与待分析信号f(t)做内积，即得到对信号f在u时间作尺度为s的小波变换：

通过Ws,uf得到原始函数f的方法为

3.1.2 基于小波变换进行多尺度分析

多尺度分析方法采用一列近似函数的极限来逼近原函数，每个近似函数都是原函数的一个平滑逼近，而且越来越接近原函数，这些函数是原函数在不同尺度上的近似，反映了不同尺度上的特征。

对于快速离散小波变换，将参数s和u进行离散化，

s=2m,u=2mk。

3.2 频繁时间模式发现方法优化

频繁时间模式发现方法的复杂度可以通过剪枝策略进一步降低。对于两个k-1维子模式P和Q，其状态按照在模式中出现的先后顺序排列后，前k-2维的状态完全相同，第k-1维状态不同，这两个子模式中的k个状态组成了一个k候选模式。算法3给出了上述过程的伪代码。

算法3搜索剪枝算法。

func candidata_generation(Fk,Ck+1,(EP)P∈Ck+1)

Ck+1=∅;n=0

for i←1 to |Fkl do

thisblock=n+1;j=Fk[i]

while Fk[i]=Fk[j] do

construct X from Fk[i] and Fk[j]

R=r∈I|X satisfies Rx[k,k-1]

for r∈R do

build k-subpatterns Slof X

if card(Ex>suppminin) then

n=n+1;Ck+1[n]=X

Ck+1[n]=thisblock

end if

end for

end while

end for

可以证明，该算法的时间复杂度为

O(k·|Fk|·|S|·(k2+log|Fk|+k·L))。

算法先在所有拥有相同k-1前缀的子模式上迭代，时间代价为O(|Fk|M)，M为最大块的大小。候选模式X的构建时间复杂度为O(k+k2)，X的k-1子串的构建复杂度为O((k-1)(k+k2))=O(k3)。k-1子模式从Fk中搜寻，时间代价为O((k-1)log|Fk|)。

算法复杂度的主要影响因素为|Fk|和L，序列长度值L取决于数据的规模。平均复杂度随k的变化而变化，当k=0和k=kmax时，复杂度取得极小值。

4 实验与分析评价

4.1 事件检测

4.1.1 模拟数据集

为了模拟一个多因素共同影响下的时间序列，用一个低频正弦波模拟低频信号，一个高频正弦波模拟噪声信号，一个脉冲信号模拟异常信号。如图3所示，将这3个信号叠加来模拟一个一般的时序数据。

为了评估算法效果，采用Savitzky-Golay平滑方法作为基线算法进行对照，用基线方法和多尺度分析方法对该模拟数据集进行状态划分，结果如图4所示。可见基线算法下，噪声信号和脉冲信号均被消除；基于小波分析的方法既能通过小尺度分析发现脉冲信号，又能通过大尺度分析消除噪声信号、发现低频信号。

4.1.2 真实数据集1——心电图数据

使用UCR数据集[9]中的“ECG200”数据，该数据为记录的受试者心电图数据，取其训练集中前10个标签为1的心跳数据进行拼接，得到本实验所用数据。

实验结果如图5所示。图5a和图5b使用的原始数据完全相同，竖直虚线表示事件间的分割点(即每两条竖直虚线之间为一个事件)。可见基线方法得到的事件信息比较混乱，不能很好地描述每次心跳过程；而多尺度分析方法能够基本完整地将每次心跳发现为一个事件，效果较基线方法明显提高。

4.1.3 真实数据集2——变电站数据

使用某变电站在2020年6月～2020年12月时间段站内机组各传感器记录的时间序列数据集。表2所示为3个标注数据上采用平滑方法和多尺度方法划分的覆盖率，可见多尺度方法的表现优于平滑方法。其中，1号数据是一个非常典型的工业时间序列数据，包括以天为周期的周期波动分量、传感器噪声、异常值；2号数据是开关柜中的臭氧浓度值，一般比较稳定，当柜内出现电弧时，会产生一个短暂的异常值；3号数据是设备温度数据，其特征明显，噪声和干扰很少。

表2 变电站数据集上的状态划分覆盖率

4.2 剪枝测试

为了测试剪枝算法的效果，创建了一个测试集，对原始算法和原始算法结合剪枝算法的新算法的运行时间进行比较。

首先对算法的优化结果进行对比，表中两列分别为原始方法和剪枝后方法在测试集上寻找k阶频繁模式(k=1,2,3,4)所需要的时间。系统环境为Window 10，CPU为Intel i5 9400 h，代码使用Python编写。测试结果如表3所示。可见k=1，2时，剪枝算法尚未生效；k=3时，剪枝算法的运行效率提升88.04%；k=4时，原算法的运行时间已经不可接受，而剪枝算法仍然可用。

表3 事件检测原算法与结合剪枝后算法的用时比较 s

时间模式长度为1和2时，剪枝方法尚未生效。对3阶频繁模式，剪枝方法能够提升88.04%的算法运行效率。k=4时，原算法运行时间已经不可接受，而剪枝后的算法仍然可用。

5 结束语

时间序列数据的事件识别是过程挖掘的重要环节之一。从时间序列出发，在已有工作基础上，通过数据预处理、状态划分和事件识别等环节，能够从多维时间序列中提取有效的事件信息，为过程挖掘工作提供数据支持。本文在已有事件提取算法基础上，主要从两方面进行了优化和改进：①引入小波分析方法，在不同频域上分解原始信号，在多个尺度上划分状态，在消除噪声信号的同时尽可能多地保留原始信号，得到了优于函数近似和平滑算法的结果；②在频繁模式发现阶段，通过数据结构的优化和剪枝策略，在不损失精度的同时提升了事件识别的效率。最后，通过模拟数据实验和真实数据集实验，验证了算法的有效性和执行效率。未来的研究方向包括对时间序列事件挖掘算法进行进一步优化改进，以及在时间序列事件信息的基础上发展更多下游应用(如业务流程发现和验证)等。