北斗二号/三号融合载波相位时间传递精度分析

于合理，李明磊，马国元，叶子玉

(电子信息系统复杂电磁环境效应国家重点实验室,河南 洛阳 471003)

0 引言

精密时间在国民经济建设等各项领域都起着重要的作用，已经成为国家重要的战略资源[1-3].精密时间具有十分重要的军事意义，2017 年美国空军战略和技术中心提出“授时战”的概念，时间的军事价值已经受到了世界各国军队的肯定和认可，并将在未来战争中发挥重要的作用，而高精度的时间传递技术是实现高精度时间系统的关键，没有高精度的时间传递就不可能使不同地方的时钟保持高精度的时间同步.全球卫星导航系统(GNSS)载波相位时间传递具有高精度、低成本、全球覆盖、全天候的特点，已经成为标准时间信号传递的主要技术手段之一.自1990 年瑞士学者Schildknecht 等提出利用GPS 进行时间传递的设想以来，文献[3-7]对GPS、GLONASS 载波相位时间传递算法进行了大量的研究.但GPS、GLONASS分别受美国国防部和俄罗斯国防部控制，其可在必要的时候伪造甚至局部停发信号，因此研究我国独立自主的北斗卫星导航系统(BDS)时间传递技术具有极其重要的意义.2020 年7 月31，北斗三号卫星导航系统(BDS-3)建成并宣布开通服务，标志着我国北斗“三步走”发展战略圆满完成，北斗迈向全球服务新时代，我国成为世界上第三个独立拥有GNSS 的国家[8-9].BDS-3 提供兼容北斗二号卫星导航系统(BDS-2)信号和新体制信号的多频导航信号，具备向全球提供导航、定位和授时(PNT)等多种服务能力.目前针对BDS 时间传递的研究主要集中在单向、双向时间传递和共视、全视时间传递[2,10-12]，但针对BDS-2/BDS-3融合载波相位时间传递的研究还比较少，因此有必要对BDS-2/BDS-3 融合载波相位时间传递性能进行研究.

1 时间传递基本原理

GNSS 载波相位时间传递一般采用精密单点定位(PPP)算法.PPP 算法通常采用消电离层组合，北斗载波相位时间传递消电离层组合观测方程如下[3,13-14]：

式中：j为卫星号；Φ、B为载波相位和伪距消电离层组合观测量；ρ 为星地距离；δt、δtj分别为接收机钟和卫星钟相对于参考时间的相对钟差；c为光速；λ、N分别为消电离层组合载波长和模糊度；T为对流层延迟；dhd(Φ)、dhd(P)分别为接收机端载波、伪距硬件延迟；分别为卫星端载波、伪距硬件延迟；分别为载波和伪距测量噪声.

卫星轨道和钟差可采用国际GNSS 服务(IGS)组织分析中心发布的事后精密产品，观测方程中未知参数为接收机三维坐标、钟差、消电离层组合模糊度和天顶对流层延迟.将观测方程线性化后可写成向量形式

式中：X为待估参数，包括接收机坐标、钟差、模糊度及对流层天顶延迟；V为观测值残差；A为设计矩阵；L为观测值向量；P为观测值权矩阵.

进行参数估计可得测站相对于参考时间北斗时(BDST)的相对钟差 δt.设参考时间为tREFT，测站r1、r2的真实时间分别为tr1、tr2.则测站r1和r2的相对钟差 δtr1、δtr2满足：

则测站r1和r2的站间时间传递结果 δtr1-r2为

将式(4)～(5)带入式(6)可得两测站的站间时间传递结果

2 试验分析

选取2020 年10 月22 日泰国曼谷帕图万(CUSV)、澳大利亚布尔迪市(MRO1)和新诺尔恰(NNOR)三个测站进行时间传递性能精度分析，采用2 种方案进行解算.方案1 仅采用BDS-2，方案2 采用BDS-2/BDS-3 融合数据处理的策略，试验中采用B1 和B3频点观测数据进行消电离层组合，观测数据采样间隔为30 s，卫星高度截止角设为10°，卫星轨道和钟差采用德国地学研究中心(GFZ)提供的精密轨道和精密钟差产品.实验采用静态模式进行处理，随机模型采用基于高度角的随机模型决定观测噪声水平，地球自转、相对论效应、天线相位缠绕、固体潮等采用相应的模型进行改正，模糊度参数采用浮点解，实验中未对接收机硬件延迟偏差进行改正.由于GFZ 提供的事后精密钟差产品的采样间隔为5 min，本文以5 min 为采样间隔对方案1 和方案2 的时间传递精度进行分析.

2.1 可见卫星数和精度衰减因子分析

以测站CUSV 为例，图1～2 分别给出了卫星高度截止角为10°时2 种方案下可视卫星数量和几何精度衰减因子(PDOP).由图1～2 可知，仅BDS-2 时，可视卫星数为8～13 颗，PDOP 值波动较大，在1.52～2.99 变化；BDS-2/BDS-3 融合解算时，可视卫星数为17～25 颗，PDOP 值在0.92～1.78 变化.BDS-3 的加入能够增加测站的可视卫星数量，改善卫星分布空间构型，可将测站CUSV 的平均可视卫星由11 颗增加到22 颗，平均PDOP 值从1.94 降低至1.15.

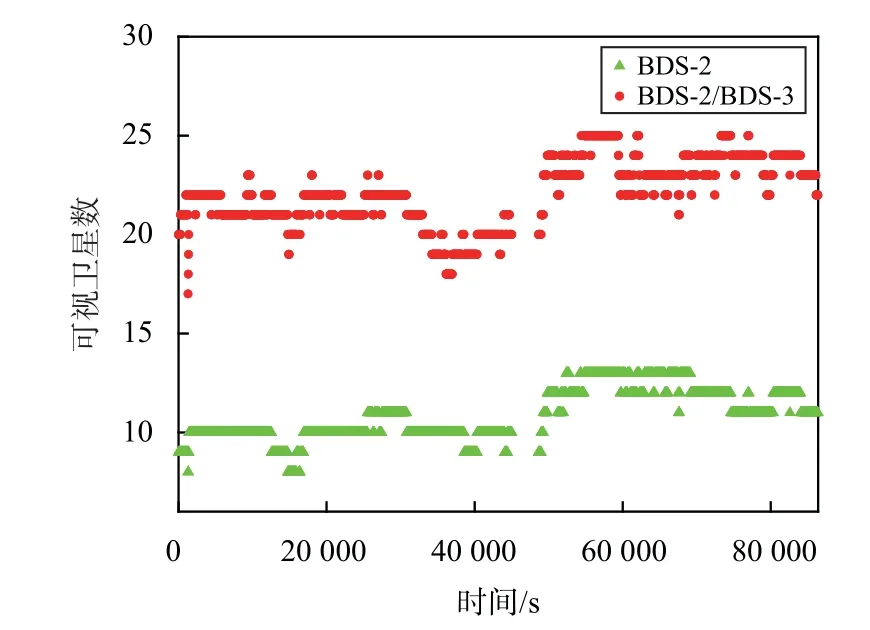
图1 CUSV 站可视卫星数

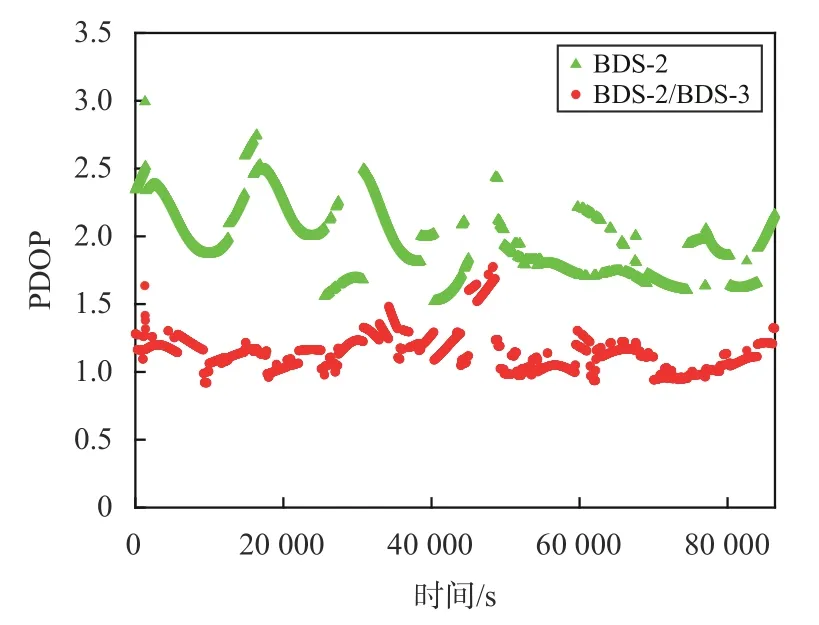
图2 CUSV 站PDOP

2.2 时间传递结果分析

采用卡尔曼滤波(KF)分别解算测站CUSV、MRO1和NNOR 的钟差结果，并将单站钟差结果进行做差可得站间时间传递结果，图3～4 给出了MRO1-CUSV和NNOR-CUSV 的站间时间传递结果.由图3～4 可知，2 种方案解算得到的时间传递结果变化趋势基本一致，但解算结果与GFZ 结果存在系统性偏差，这主要是因为解算时未对接收机的硬件延迟偏差进行改正，同时采用不同数据处理方法也会使结果存在一定的系统性偏差.将2 种方案时间传递结果与GFZ 最终结果作差可计算得到站间时间传递结果的差值序列，为更好地分析时间传递结果，图5～6 给出了消除系统性偏差后MRO1-CUSV 和NNORCUSV 的时间传递结果差值序列.表1 给出了MRO1-CUSV 和NNOR-CUSV 站间时间传递结果的标准差，表2 给出了MRO1-CUSV 和NNOR-CUSV 站间时间传递结果的A 类不确定度.

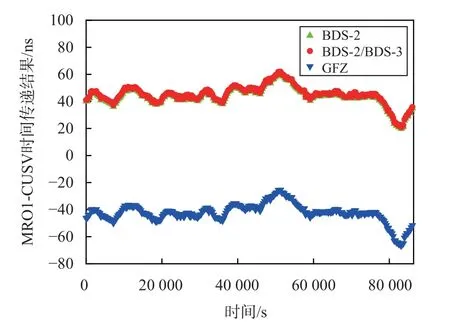
图3 MRO1-CUSV 时间传递结果

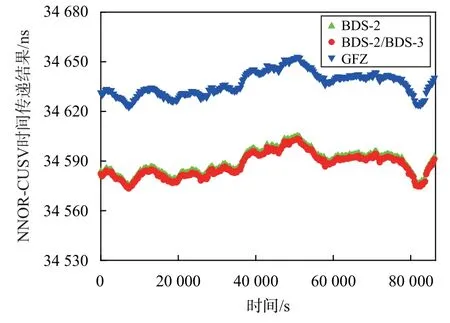
图4 NNOR-CUSV 时间传递结果

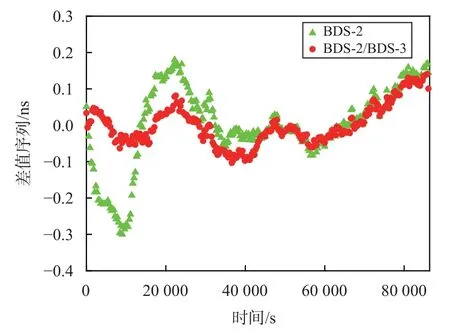
图5 MRO1-CUSV 时间传递结果的差值序列

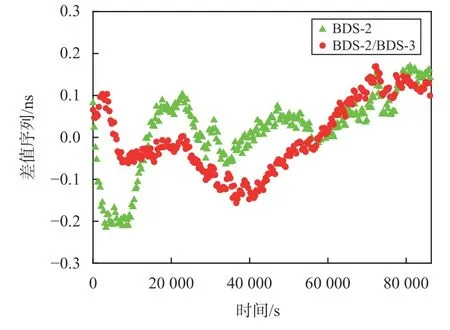
图6 NNOR-CUSV 时间传递结果的差值序列

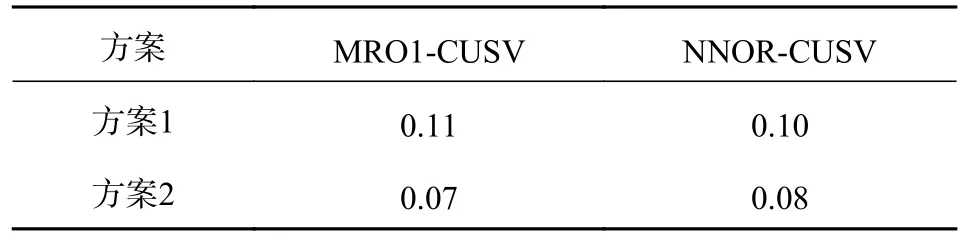
表1 两种方案结果的标准差 ns

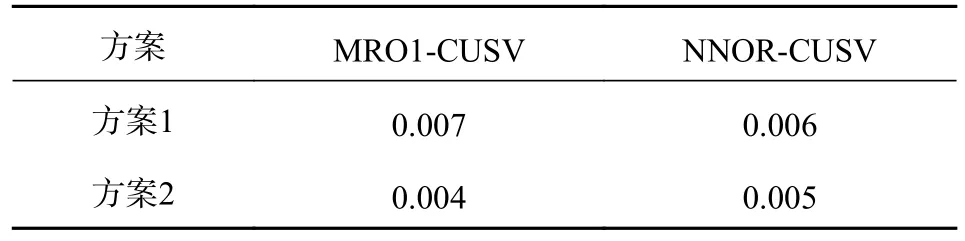
表2 两种方案结果的A 类不确定度 ns

由图5～6、表1～2 可知，2 种方案计算的时间传递结果变化趋势基本一致，BDS-2/BDS-3 融合解算时间传递结果优于单BDS-2 解算的时间传递结果.方案2 相比方案1 能够将MRO1-CUSV 和NNORCUSV 时间传递精度分别从0.11 ns、0.10 ns 提高到0.07 ns、0.08 ns，精度分别提高36%和20%.BDS-2/BDS-3 融合时间传递能够将MRO1-CUSV 和NNORCUSV A 类不确定度分别从0.007 ns、0.006 ns 提高到0.004 ns、0.005 ns，精度分别提高42%和17%.

3 结束语

随着BDS-3 建成并宣布开通服务，有必要对BDS-2/BDS-3 融合载波相位时间传递精度进行分析.文中给出了载波相位时间传递基本模型，并利用GFZ 发布的卫星精密产品和测站CUSV、MRO1、NNOR 的观测数据，通过具体试验分析了BDS-2/BDS-3 融合时间传递性能.结果表明：BDS-3 的加入能够增加测站的可视卫星数量，改善卫星分布空间构型，可将测站CUSV 的平均可视卫星由11 颗增加到22 颗，平均PDOP 值从1.88 降低至1.15.BDS-2/BDS-3融合解算时间传递结果优于仅利用BDS-2 的时间传递结果.可将MRO1-CUSV 和NNOR-CUSV 的时间传递精度分别从0.11 ns、0.10 ns 提高到0.07 ns、0.08 ns，A 类不确定度分别从0.007 ns、0.006 ns 提高到0.004 ns、0.005 ns.