阳江地区黏性土物理力学指标的统计分析

胡亚晴，周小龙*，潘胜平，赵 勇，李元松

1.武汉工程大学土木工程与建筑学院，湖北 武汉 430074；

2.中铁大桥局集团第五工程有限公司，江西 九江 332001

风能属于清洁的可再生能源，风力发电潜力巨大，且没有碳排放等环境成本，随着陆上风电资源可开发量的逐渐减小，海上风电成为各国大规模新能源转型的重要方向。吸力桶基础由于具有可重复利用、施工方便、经济性好等优点，被广泛应用于海上风力发电风机结构基础中［1］。

吸力桶沉贯控制是风机基础设计和施工中的一大难题，而准确确定沉贯阻力是吸力桶基础安全施工的主要前提［2］。对于黏性土，美国工程设计规范API［3］指出吸力桶基础沉贯阻力与土体的不排水抗剪强度和有效重度有关；挪威船级社DNV［4］推荐的计算公式表明吸力桶基础沉贯阻力与土层锥尖阻力有关；国内研究成果也表明，土层抗剪强度对桩侧摩阻力的影响较大［5-7］，同时王庚荪等［8］、丁红岩等［9］提出吸力桶负压沉贯引起的渗流梯度，不仅改变土体渗透性，甚至改变了土体物理力学特性；文献［10-11］表明含水率对桩侧摩阻力影响较为显著，且不同地区桩侧摩阻力随含水率变化发展规律不同。Shi 等［12］研究发现孔隙比、液性指数对桩侧摩阻力的影响较大。综上，不同特性的土层，吸力桶基础沉贯阻力考察土层物理力学指标存在差异，即使对于同一类土，不同区域其工程力学特性也可能不一致［13-15］。可见，吸力桶基础的沉贯特性是研究所关注的焦点，由于地质环境的差异，土体特性的地域离散性非常突出，若无针对特定地质环境的吸力桶基础沉贯特性的研究，就难以保证吸力桶的施工质量与安全。

本文以广东省阳江市沙扒镇某近海海上风电项目为背景，以该工程区域内第四系全新世冲海积物（Q4m+al）黏性土为研究对象，分析阳江地区风电场黏性土土层特性，为特定地质环境土体的吸力桶基础沉贯特性分析提供参考。

1 黏性土物理力学指标统计分析

本文土体取土区域为广东省阳江市阳西县沙扒镇附近海域，海水深度约27 m，取土深度为21 m，以该区域55 个岩土工程勘察钻孔资料为数据基础，统计分析黏性土的物理力学指标。选取的物理指标有含水率w、有效重度γ′、孔隙比e、液限WL、塑限WP、液性指数IL及塑性指数IP；力学指标有压缩模量Es、直剪条件下黏聚力c和内摩擦角φ。在取土深度范围内，有黏性土也有无黏性土，本文选取的数据均为黏性土的数据。该地区黏性土土层分布为：①1层为淤泥，①2层为淤泥质黏土，①3、②2、②4、②6层均为黏土。

经过统计整理，得到该地区黏性土物理力学指标分层统计结果，如表1 所示。

由表1 可知，阳江地区黏性土具有以下特征：

表1 黏性土物理力学指标统计表Tab.1 Statistics of physical and mechanical indexes of cohesive soils

（1）含水率、孔隙比高。含水率的平均值在31.7%～45.3%之间，标准差在3～4 之间，表明黏性土含水率较高且离散程度较大，亲水矿物较多；孔隙比平均值在0.83～1.24 之间，说明土体压缩性偏高，即土体结构强度差；阳江地区黏性土具有较高的含水率和孔隙比，对土体的变形特征和强度特征有影响。WL和WP均值分别介于36%～50.3%和17.5%～25.6%之间，IL和IP变化范围分别为0.42～1.35 和10.5～22.0，其中淤泥土层状态为流塑，淤泥质黏土土层状态为流塑到软塑，黏土土层状态为可塑。

（2）压缩性较高。黏性土压缩模量的变化范围为2.00～5.06 MPa，属于高压缩性土，这也反映了该地区黏性土的孔隙比大。

（3）①1、①2、①3、②2、②4、②6层黏性土黏聚力平均值分别为7.6、17.9、28.4、46.3、48.1、46.4 kPa，内摩擦角平均值分别为18.6°、8°、17.6°、17.7°、14.8°、11°。该地区黏性土与广东省其他地区［16-18］黏性土相比力学特性较好，淤泥及淤泥质黏土的抗剪强度较小，力学特性较差。

（4）物理指标的变异系数小，离散程度小，说明该地区黏性土的物理性质较稳定。力学指标的变异系数大，离散程度大，说明该地区黏性土的力学性质不够稳定。从整体上来看，物理性质指标统计参数的平均值具有一定的代表性，可以作为该地区工程应用的参考依据。

2 黏性土物理力学指标相关性分析

阳江市黏性土的内摩擦角较小，因此抗剪强度指标近似采用黏聚力表征。该地区黏性土有效重度取水下浮重度。本文采用数理统计法研究黏聚力、有效重度与其他物理力学指标间的关系以及它们的分布规律，据此分析吸力桶基础沉贯阻力计算时应考虑的指标，对工程实践具有重要意义。

本文采用一元线性回归法研究物理力学指标间的关系，并确定最合适的关系式，作为检验和预测指标的经验关系式。采用Pearson 相关系数对物理力学指标之间的相关程度进行评判，按照相关系数的大小，可将变量之间的相关程度分为以下几种情况［19］：当|R|≥0.8 时，为高度相关；0.5≤|R|＜0.8 时，为中度相关；0.3≤|R|＜0.5 时，为低度相关；|R|＜0.3 时，可视为不相关。

2.1 物理指标之间的相关性分析

含水率和孔隙比与有效重度的拟合曲线分别如图1（a）和图1（b）所示。由图1（a）可知，有效重度与含水率和孔隙比表现为高度负相关，拟合曲线精度较高。由《工程地质手册》［20］中浮重度的计算公式可知，浮重度与含水率、孔隙比成反比，与拟合结果一致。

图1 有效重度与物理指标的一元线性回归分析曲线：（a）含水率，（b）孔隙比Fig.1 Univariate linear regression analysis curves between effective unit weight and physical indexes：（a）water content，（b）void ratio

采用同样的方法对有效重度与其他物理指标之间的关系进行分析，分析结果列于表2 中。

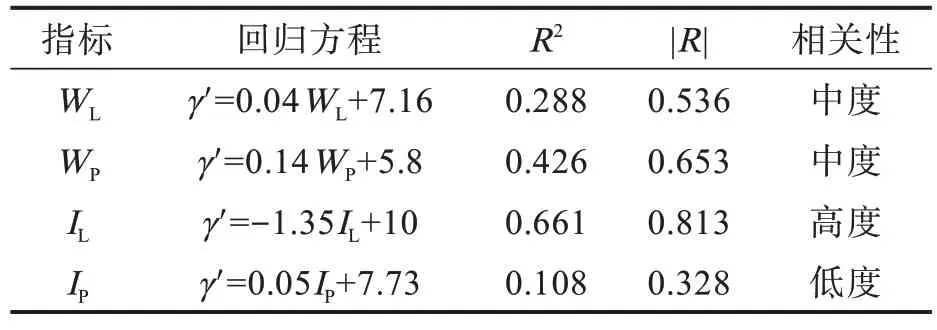
表2 有效重度与物理指标相关性分析结果Tab.2 Results of correlation analysis between effective unit weight and physical indexes

由表2 可知，有效重度与液性指数IL之间表现为高度负相关，与液限WL、塑限WP和塑性指数IP之间表现为正相关，但相关性较低。

2.2 物理指标与力学指标之间的相关性分析

黏聚力与含水率的拟合曲线如图2（a）所示，黏聚力随含水率的增大呈现线性减小的趋势。可见，对于黏性土，增大含水率，使其表面的结合水膜变厚且自由水增多，致使土颗粒间的结合力和摩擦力减小，润滑作用增强，从而削弱了土的黏聚力［21］。

黏聚力与孔隙比的拟合曲线如图2（b）所示，随着孔隙比的增大，黏聚力呈现减小趋势。孔隙比反映了土体的密实程度，孔隙比越大，土体越松散，土颗粒间距增大，土颗粒间的范德华力减小且结合水膜对土体的粘结作用被削弱，使得土的黏聚力减小［22］。

图2 黏聚力与物理指标的一元线性回归分析曲线：（a）含水率，（b）孔隙比Fig.2 Univariate linear regression analysis curves between cohesion and physical indexes：（a）water content，（b）void ratio

采用同样的方法对阳江地区黏性土黏聚力与其他物理指标之间的相关性进行分析，分析结果列于表3 中。

表3 黏聚力与物理力学指标相关性分析结果Tab.3 Results of correlation analysis between cohesion and physical and mechanical indexes

综上可知，黏聚力c与液限WL、塑限WP、塑性指数IP及压缩模量Es之间呈正相关，相关性不高。黏聚力c与含水率w、孔隙比e、液性指数IL之间呈负相关，与文献［23-24］的成果一致。黏聚力随含水率、孔隙比、液性指数的增加而减小，呈高度线性相关，拟合曲线精度高，可用于该地区黏性土物理力学指标的估计和校验。

总体而言，对有效重度和黏聚力影响较大的物理指标为含水量、孔隙比和液性指数。因此，在计算阳江地区吸力桶基础沉贯阻力时，不仅要重点研究有效重度及不排水抗剪强度，还需考虑含水率、孔隙比及液性指数等物理指标的影响。

3 黏性土物理力学指标随土层分布深度的变化

本文采用回归分析法分析物理力学指标与土层分布深度（h）之间的关系，研究该地区黏性土沿土层分布深度方向的工程性质。物理力学指标随土层分布深度的变化曲线如图3 所示。

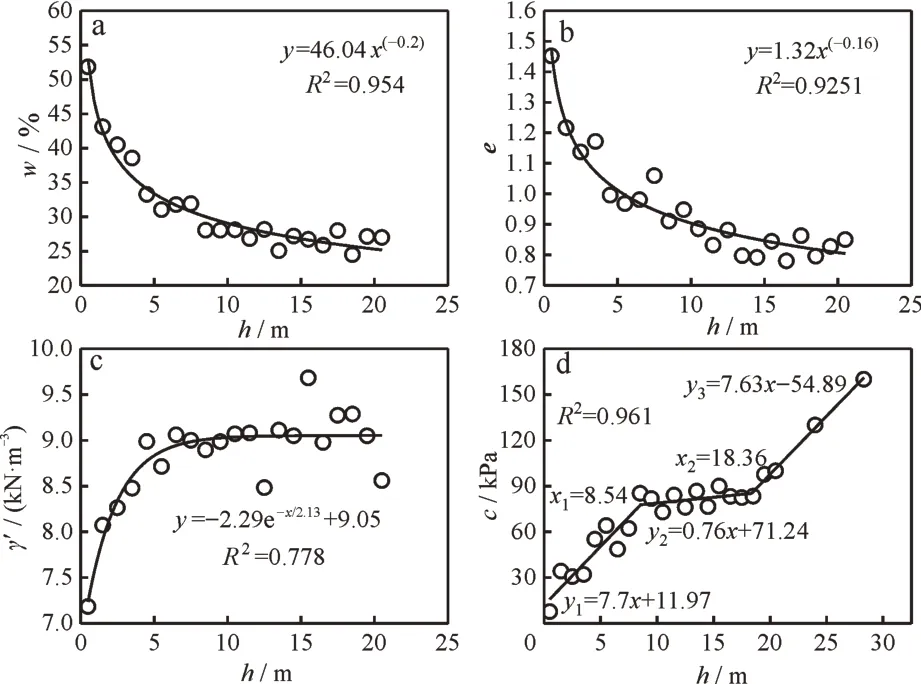
图3 物理力学指标与土层分布深度的回归分析曲线：（a）含水率，（b）孔隙比，（c）有效重度，（d）黏聚力Fig.3 Regression analysis curves of physical and mechanical indexes and depth of soil layer distribution：（a）water content，（b）void ratio，（c）effective unit weight，（d）cohesion

含水率及孔隙比随土层分布深度变化的曲线分别如图3（a）和图3（b）所示，孔隙比及含水率与土层分布深度之间的相关性较好，曲线拟合精度高，均大于0.9，可为工程实践提供参考依据。孔隙比及含水率随土层分布深度的增加逐渐减小，且逐渐趋于稳定。该地区土体的分布特征表现为：在土层分布深度小于8 m 时，绝大部分为黏性土层，随着土层分布深度的继续增加，无黏性土逐渐出现且占比越来越高。在0～8 m 范围内，含水率和孔隙比随土层分布深度的增加逐渐减小，且递减速度逐渐放缓，在8～21 m 范围内，随着土层分布深度的增加，含水率和孔隙逐渐趋于稳定。

有效重度随土层分布深度的变化如图3（c）所示，有效重度随土层分布深度的增加呈现出先增加后趋于稳定的趋势。由图1 可知，有效重度与含水率和孔隙比之间呈现较强的负相关性，其与土层分布深度也表现出相似的性状。在0～8 m 范围内，随着土层分布深度的增加，含水率及孔隙比逐渐减小，因此，有效重度随土层分布深度的增加逐渐增大，在8～21 m 范围内，随着土层分布深度的增大，有效重度趋于稳定。

黏性土黏聚力随土层分布深度的变化曲线如图3（d）所示，二者之间的相关系数R为0.928，为高度相关，拟合曲线精度为0.961，拟合效果好，可为工程提供参考依据。黏聚力随土层分布深度呈台阶型增长，增长速率先减小再增大。在0～8 m范围内，含水率与孔隙比对黏聚力的影响程度大，黏聚力随土层分布深度的增加而增加；在8～17 m范围内，黏聚力随土层分布深度增加趋于稳定；在17～21 m 范围内，黏聚力再次随土层分布深度的增加而增加。

由土体的物理力学指标随土层分布深度的变化曲线可知，阳江地区黏性土的含水率、孔隙比均随土层分布深度的增加而减小，黏聚力则随土层分布深度的增加而增大，说明黏性土在沉积过程中，固结和压密正常，土体工程性质较好。

4 结论

本文统计分析了阳江地区黏性土物理力学指标，采用回归分析和相关性分析的方法对物理力学指标之间及其与土层分布深度之间的关系进行了研究，得到以下结论：

（1）阳江地区黏性土的特征为：含水率、孔隙比、液限、塑限、液性指数、塑性指数的值均较高，压缩性较大。物理指标的离散程度小于力学指标。

（2）有效重度和黏聚力与含水率、孔隙比和液性指数呈负相关且相关性强，与液限、塑限和塑性指数、压缩模量呈负相关且相关性弱。

（3）有效重度随土层分布深度的增加呈现出先增加后趋于稳定的趋势。黏聚力与土层分布深度呈正相关，增长趋势为台阶型，且与土层分布深度呈高度相关性。

（4）在进行吸力基础桶沉贯阻力计算时，除考虑不排水抗剪强度和有效重度外，还应考虑孔隙比、含水率及液性指数对阻力的影响。

由于收集到的数据有限，本文只讨论了物理力学指标之间的关系，物理力学指标与原位试验结果、标准贯入值之间的关系未做讨论，有待今后进一步研究和分析。