基于有限元极限平衡法的三维边坡稳定性

苏振宁，邵龙潭

大连理工大学工业装备结构分析国家重点实验室，大连 116024

边坡稳定分析是岩土工程中的重要课题.通常三维空间中的边坡选取典型断面并假设断面处于平面应变条件，从而进行二维稳定分析[1].二维分析导致结果偏于保守，且不能反映边坡破坏的三维特性.许多学者开展了三维边坡稳定分析方法的研究，有满足三个方向上的力和力矩平衡的严格三维极限平衡法[2-6]，也有用于三维边坡稳定分析的强度折减法[7-10].

葛修润[11]指出极限平衡法和强度折减法都建立在强度折减的概念上，存在许多不合理之处，故在“真实”应力状态的基础上提出了矢量和法并进行了一系列研究[12-13].“真实”应力状态是指采用数值方法根据未折减的土体强度参数计算得到的应力场.也有学者在真实应力状态下提出了安全系数为剪应力比形式的三维稳定分析方法[14-16]，该形式的安全系数，理论基础不牢固，仅在滑动面是球形或椭球形时，安全系数才具有力矩比的物理意义[17].

在二维边坡稳定分析中，邵龙潭和李红军[18]将一点极限平衡条件扩展到沿滑动面的整体极限平衡条件，根据该条件定义了安全系数，明确了其物理意义，建立了有限元极限平衡法，并将其用于各类土工结构的稳定分析[19].该方法理论体系严密，应力场真实，能适用于任意形状的滑动面.

本文将有限元极限平衡法扩展到三维，提出了三维滑动面上一点在滑动方向上的极限平衡条件，证明了沿滑动面的整体极限平衡等价条件.给出了主滑方向的确定方法以及基于主滑方向的滑动方向计算方法.基于极限平衡条件定义了局部和整体安全系数.最后通过算例验证了本文方法的合理性、有效性以及对任意形状滑动面的适应性.

1 极限平衡条件

1.1 一点滑动方向上的极限平衡条件

极限平衡状态是研究对象即将失去而未失去平衡的状态，极限平衡法和强度折减法都通过折减强度参数的方法，使边坡达到极限平衡状态.极限平衡法中的极限平衡状态为滑动面上每个点在滑动切平面上的剪应力都等于抗剪强度，强度折减法的极限平衡状态判断则根据失稳判据主要分成3 种[20]：数值解非收敛、塑性区贯通和位移突变.采用有限元极限平衡法对边坡进行稳定分析，因为应力场真实（非极限平衡状态），所以需要对极限平衡状态进行预估.

在二维平面应变问题中，滑动面切平面决定剪应力方向和抗剪强度方向.剪应力方向沿滑动面切向指向滑动方向.无论是非极限平衡状态还是极限平衡状态，剪应力只有大小变化没有方向变化，如图1(a).

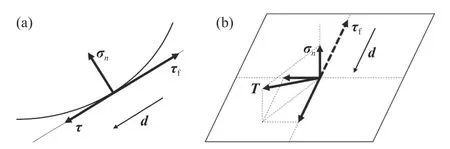
图1 滑动面应力分析.(a)二维；(b)三维Fig.1 Stress on a slip surface: (a) two-dimensional;(b) threedimensional

在三维中，滑动面上一点的法向正应力和剪应力可根据该点处应力张量和滑动面切平面法向量计算：

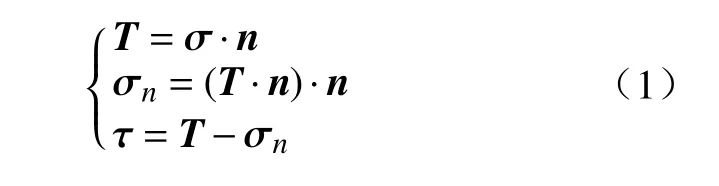
式中，σ为该点处应力张量，n为滑动面切平面的法向单位矢量，T为应力矢量，σn为法向正应力矢量，τ为剪应力矢量.当滑动面确定后，由非极限平衡状态向极限平衡状态的变化过程中，法向正应力矢量方向不变，但剪应力矢量方向在滑动面的切平面上变化.根据Chen 的研究[21]，土体发生塑性应变时剪应变与剪应力可假定为同向.所以假设极限平衡状态时剪应力方向与位移方向一致，即为滑动方向.需注意的是，各点的滑动方向是在滑动面切平面上的方向，每个点切平面的法方向不同，滑动方向也不同.若确定了滑动方向，非极限平衡状态下的滑动面应力如图1(b)所示.其中τf是极限平衡状态的抗剪强度矢量.在极限平衡状态下，考虑在滑动方向上有：

式中，d是一点滑动方向矢量，因为 σn垂直于滑动面，d在滑动面上，所以 σn·d=0，保持左右两侧一致，并考虑到τf与d方向相反，式（2）变为

式（3）为一点在滑动方向上处于极限平衡状态的条件.

1.2 滑动面整体极限平衡条件

任意滑动面上土体整体达到极限平衡状态与滑动面上土体各处在滑动方向上处于极限平衡状态等价.滑动面整体达到极限平衡状态定义为：

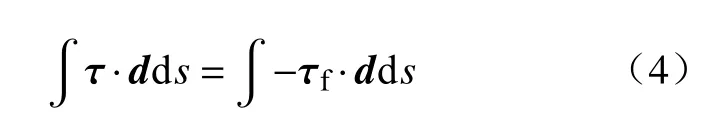
式（3）在滑动面上处处成立与式（4）的等价，证明如下：

如果滑动面上各处都在其自身的滑动方向上处于极限平衡状态，即满足式（3），则对滑动面上微元有

对式（5）两侧进行积分，所以式（4）成立.

反过来，如果式（4）成立，考虑到积分符号内为标量，并且矢量点乘有结合律，则有

因为对于稳定或者处于极限平衡状态的土体，每一点都必有

且 ds＞0，则要使式（6）成立，必须积分域上处处满足：

所以滑动面上每一点都满足式（3）.

需要注意，即使当滑动面上各点的剪应力矢量的大小都等于抗剪强度，整个滑动面也不是处于极限平衡状态.滑动方向意味着一个运动许可方向，只有当各点的剪应力矢量方向指向滑动方向且大小等于抗剪强度时，整体滑动面才处于极限平衡状态.

2 滑动方向与主滑方向

滑动面上不同点有不同的滑动方向d.滑动面上各点滑动方向的计算方法是本文方法的关键点之一.需要根据现有的有限元计算结果，得到合理的滑动方向.

滑动方向的计算需要用到主滑方向的概念.Kalatehjari 等[22]根据极限平衡法的基本假定之一，刚体滑动体假定，阐明了三维边坡滑动存在唯一的主滑方向.主滑方向被定义为极限平衡状态下，滑坡体滑动方向的水平投影方向.主滑方向不同于滑动方向，主滑方向是定义在XOY平面上，每一个滑动面只对应一个主滑方向.现对唯一主滑方向的合理性进行说明：

对滑动体进行垂直条分，根据假定每个条分柱体都是刚体.在极限平衡状态下，假设每个柱体运动方向的水平投影有3 种情况：平行、聚拢和分离.刚体假设阻止了柱体聚拢，而柱体分离则意味着柱体间没有力的相互作用，力和力矩平衡被打破，这与实际情况不符.所以互相平行的柱体运动方向水平投影是唯一的选项.

在三维极限平衡法中，很多方法对条柱底面的极限剪应力方向也有类似假定，比如要求剪应力平行于XOZ平面[23-24]或剪应力在XOY平面内的投影方向保持一致[5-6,22].极限平衡法是通过折减材料强度参数获得满足力和力矩平衡的极限状态从而计算安全系数的方法，底面剪应力方向就是极限状态时的滑动方向.在非极限状态下，本文根据真实应力场计算滑动面上的剪应力没有这种方向一致性，但通过主滑方向计算得到的滑动方向，正是对极限状态时滑动方向的预估，也是对极限状态时剪应力方向的预估.

滑动面上各点的滑动方向可以根据唯一的主滑方向计算.根据滑动方向处于滑动面上；滑动方向在XOY平面的投影是主滑方向；滑动方向是单位矢量，可以联立方程计算滑动方向单位矢量：

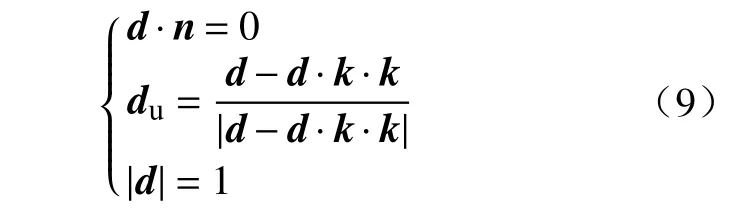
式中，du是主滑方向矢量，k是Z方向的单位矢量.3 个方程可以求解滑动方向矢量d的3 个元素.

通过非极限平衡状态的滑动面应力场对极限平衡状态推测得到主滑方向，可以将滑动面剪应力矢量的和矢量的水平投影方向作为主滑方向，用公式表示为：

主滑方向的选取具有一定的主观性，比如设计人员认为边坡在未来会受到某一方向的荷载，从而产生沿某一特定方向的破坏，那么要考虑这一特定方向的安全系数，就可以将这一特定方向设为主滑方向进行计算.

3 局部和整体安全系数定义

安全系数是对研究对象距离极限平衡状态的描述，安全系数等于1 则认为研究对象处于极限平衡状态.根据对一点在滑动方向上处于极限平衡状态的定义，一点处的局部安全系数被定义为：

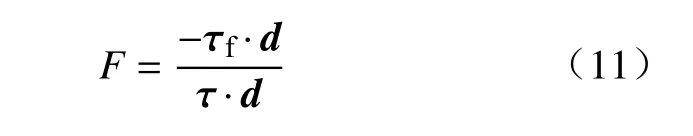
式（11）表示一点安全系数是抗剪强度与剪应力在滑动方向上的投影的比，其物理意义是一点在滑动方向与极限平衡状态的距离，也是一点在滑动方向上强度的储备.

F(s)是 在滑动面s上的局部安全系数函数，在各点符合式（11）的定义，可使滑动面上土体微元均达到极限平衡状态，那么土体在滑动面s上整体达到极限平衡就变为

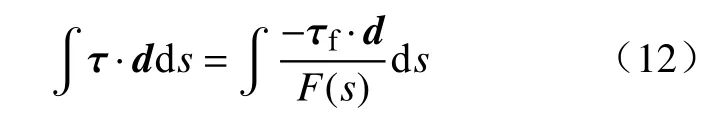
应用积分中值定理，式（12）右侧变为：

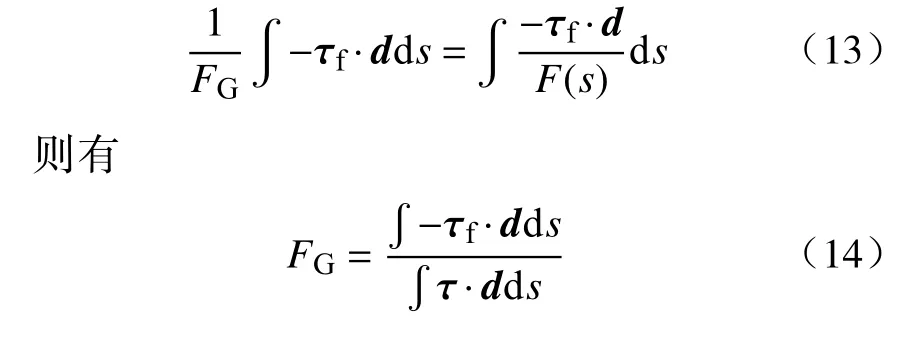
FG是整体安全系数，表征滑动面上各点局部安全系数的中值.在推导整体安全系数的定义中，对滑动面形状和对称性未做要求，所以方法可以用于任意形状滑动面的安全系数计算.

二维情况下，因为 τ和d方向相同，τf和d方向相反，式（9）退化为

这是在基于应力的二维边坡稳定分析方法中被广泛使用的全局安全系数定义式，也是有限元极限平衡法的安全系数定义[18].

三维情况下，剪应力比形式的安全系数定义为：

对比安全系数定义式（16）和式（14），如果假定 τ和d方 向相同，τf和d方向相反，式（14）可以退化为式（16）.这种假定隐含剪应力矢量方向在非极限平衡状态和极限平衡状态相同的设定，对倾向滑动方向的滑动面，剪应力矢量方向变化不大，但对倾向方向偏离滑动方向的滑动面，剪应力矢量方向在非极限平衡状态和极限平衡状态差距很大，这会导致误差，这也是采用式（16）定义安全系数的限制.

4 计算方法

本文方法需要计算边坡区域的应力场，并基于应力计算边坡的安全系数.有限元法可以根据本构关系计算应力场.在本文中，有限元本构使用线性弹性理想塑性模型，计算软件为商业有限元软件Abaqus 6.14.理想的塑性屈服准则与Mohr-Coulomb 破坏准则一致.抗剪强度采用Mohr-Coulomb 计算：

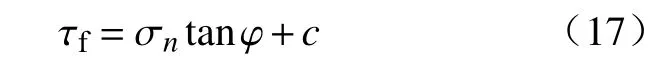
式中，σn为 法向正应力，φ为摩擦角，c为黏聚力.

在计算过程中需要对滑动面上的变量进行积分.数值积分需要对滑动面进行离散，对滑动面进行网格划分.在这里选择将滑动面划分为三角形网格，原因是三角形网格比四边形网格更容易计算滑动面的法线方向并更准确地描述滑动面，在边界处也更容易分割.通过3 个步骤构造滑动面，如图2 所示.

图2 滑动面构造步骤.(a)三角形网格；(b)网格节点调整；(c)滑动面与坡面相交Fig.2 Construction steps of the slip surface: (a) triangle mesh;(b) mesh node adjustment;(c) slip surface intersects the slope surface

第一步：在XOY平面中创建三角形网格；

第二步：通过插值将三角形网格节点的z坐标从XOY平面调整到构造表面的位置；

第三步：获得坡面与三角形网格的交点，三角形网格被分割，模型内部的部分被保留，作为滑动表面.

另一种方法是，如果滑动面在有限元模型中已经被划分（比如滑动面是岩体结构面或确定的软弱层），则可以直接将滑动面位置的四面体单元表面的三角形网格提取出来，作为滑动面网格使用；如果有限元采用的是六面体单元，则可以将四边形表面从中剖分，得到两个三角形网格单元.

滑动面三角形网格中心点应力张量由有限元网格节点处应力张量插值计算，插值方法选用三维线性插值.本文方法安全系数计算流程如图3所示.

图3 安全系数计算流程Fig.3 Flowchart of the safety factor calculation

5 算例

算例中将采用式（16）剪应力比形式定义的安全系数记作F1，将采用式（14）定义的安全系数记作F2.

5.1 算例1

算例1 来自Fredlund 和Krahn[25]对二维边坡的研究，有学者将这一算例拓展到三维情况并进行了研究.该算例包含2 种工况，一种是均质边坡，滑动面为椭球形；一种是带软弱薄层的边坡，滑动面为椭球型和位于软弱薄层的平面组合.椭圆的长轴为133.8 m，有限元模型y轴方向的长度为110 m，其他相关参数如图4 所示，图中γ为重度，E为弹性模量，v为泊松比，H为坡高，β为坡角，R为短轴半径.横向边界条件为约束Y轴方向位移（平面应变）.图5 展示滑动面网格和有限元网格尺寸对安全系数的影响.随着滑动面网格尺寸从4 减小到0.75 m，安全系数逐渐减小并稳定，有限元网格尺寸从4 减小到1 m，安全系数略有减小.图6 和图7 分别展示工况1 的滑动方向和剪应力矢量方向，通过对比可见两者方向基本一致，只在侧面靠近坡面处略有差别.因此表1 中F1与F2在工况1 下基本一致.

表1 算例1 的安全系数比较Table 1 Comparison of the safety factors computed for example 1

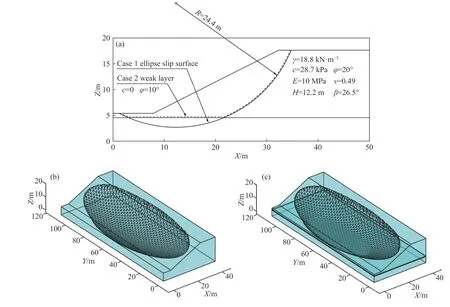
图4 算例1.(a)材料参数和断面；(b)工况1；(c)工况2Fig.4 Example 1: (a) material parameters and cross-section;(b) case 1;(c) case 2

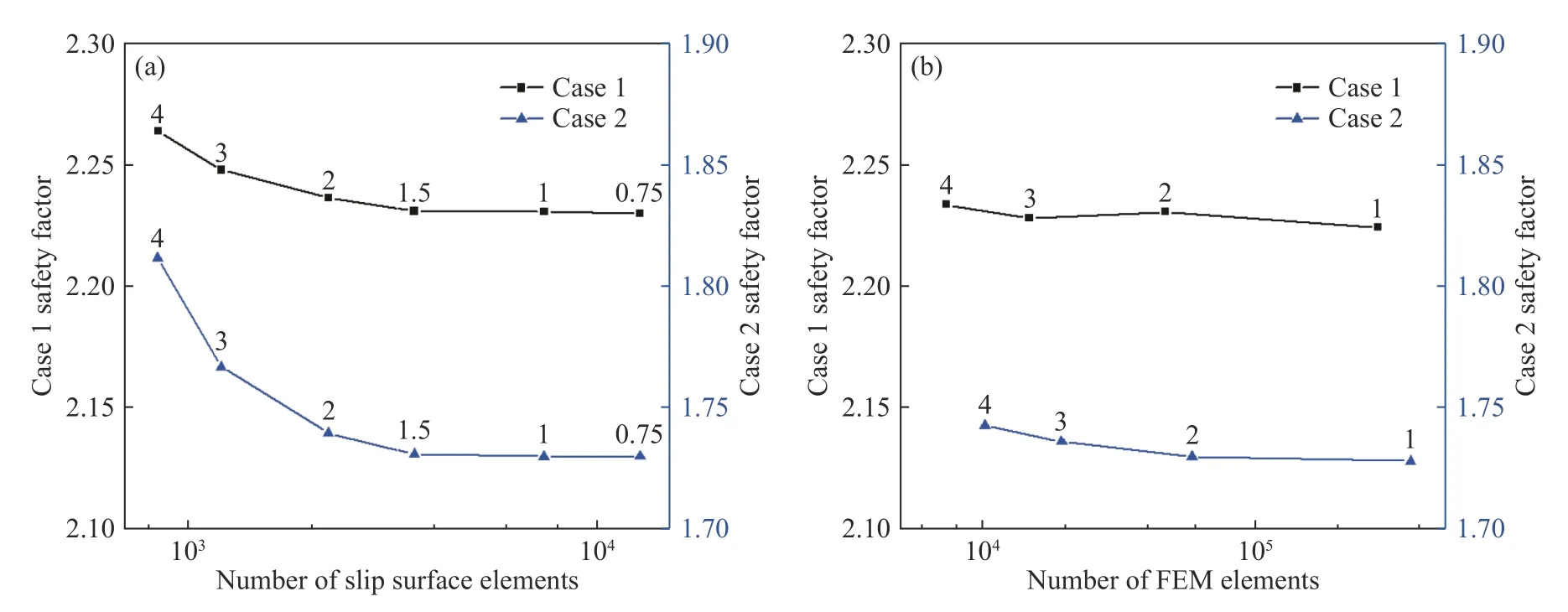
图5 单元数对安全系数的影响.(a)滑动面；(b)有限元Fig.5 Influence of the number of units on the safety factor: (a) slip surface;(b) FEM

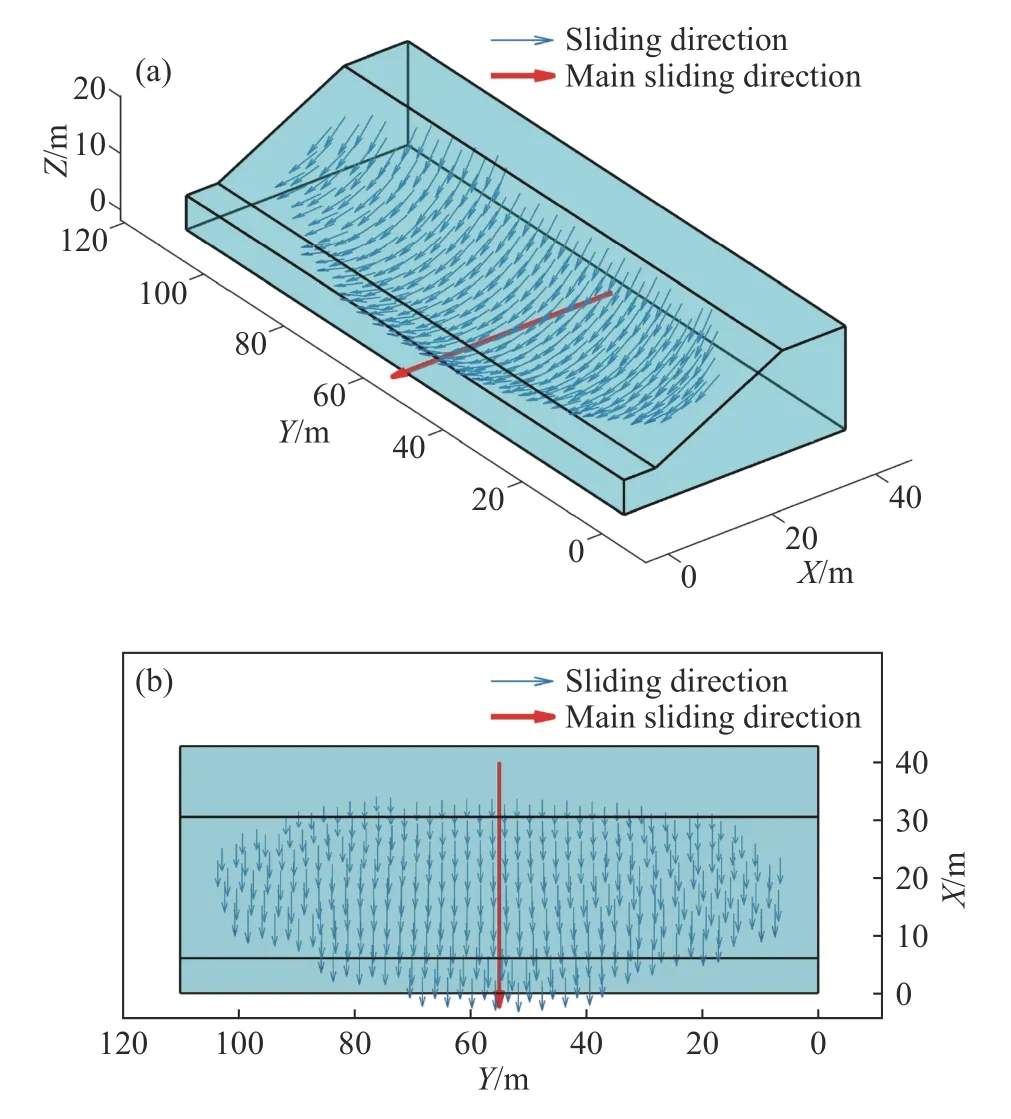
图6 工况1 的滑动方向与主滑方向.(a)等轴测图；(b)俯视图Fig.6 Sliding direction and the main sliding direction of case 1: (a)isometric view;(b) top view

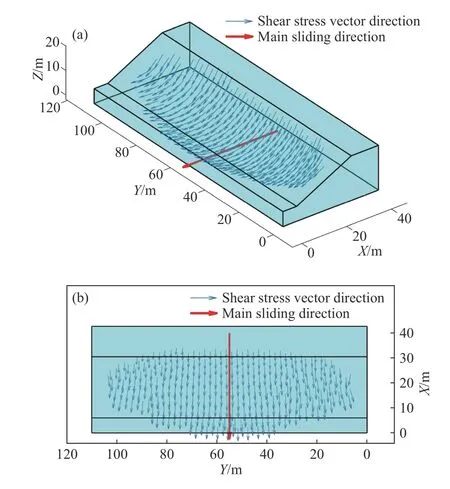
图7 工况1 的剪应力矢量方向与主滑方向.(a)等轴测图；(b)俯视图Fig.7 Shear stress vector direction and the main sliding direction of case 1: (a) isometric view;(b) top view

5.2 算例2

楔形体破坏是三维岩石边坡破坏的常见情况.如图8 所示，这里使用两个典型的楔形破坏算例[26]来验证本文方法的合理性.算例包括具有对称结构表面的楔形体和具有非对称结构表面的楔形体.算例的材料参数和几何信息列于表2 和表3中.通过图9 和图10 的对比可以明显看出，在非极限平衡状态下，剪应力矢量方向与滑动方向不一致，所以导致表4 中F1结果小于其他方法安全系数.Hoek-Bray 解是一个静力平衡解，一般被认为是该算例的理论解，本文方法和严格极限平衡法都与理论解一致，但F1小于理论解，有较大误差.

表4 算例2 的安全系数比较Table 4 Comparison of the safety factors for example 2

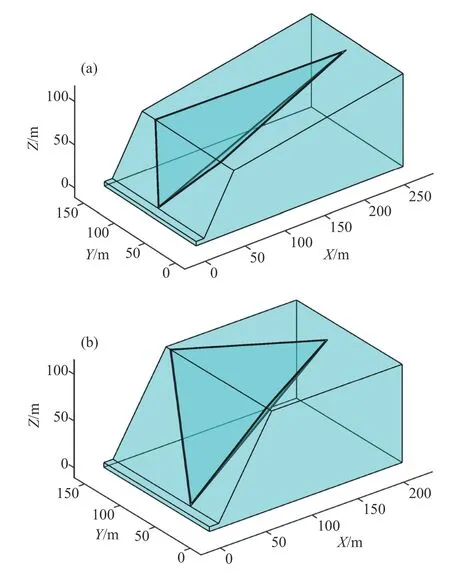
图8 算例2 楔形体破坏.(a)对称楔形体；(b)非对称楔形体Fig.8 Example 2: wedge failure: (a) symmetric wedge;(b) asymmetric wedge

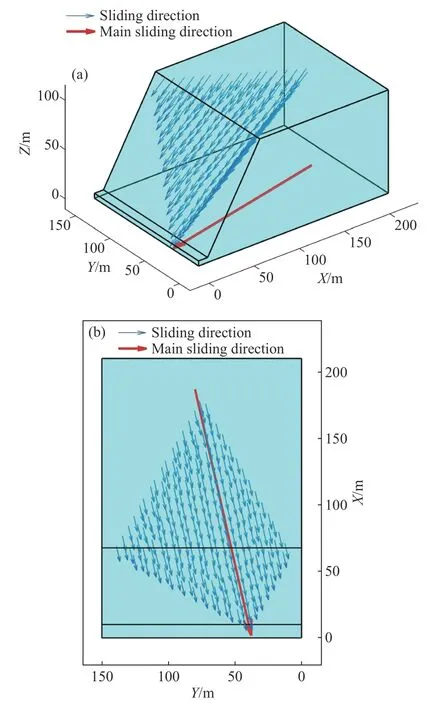
图9 非对称楔形体的滑动方向与主滑方向.(a)等轴测图；(b)俯视图Fig.9 Sliding direction and the main sliding direction of an asymmetrical wedge: (a) isometric view;(b) top view

图10 非对称楔形体的剪应力矢量方向与主滑方向.(a)等轴测图；(b)俯视图Fig.10 Shear stress vector direction and the main sliding direction of an asymmetrical wedge: (a) isometric view;(b) top view

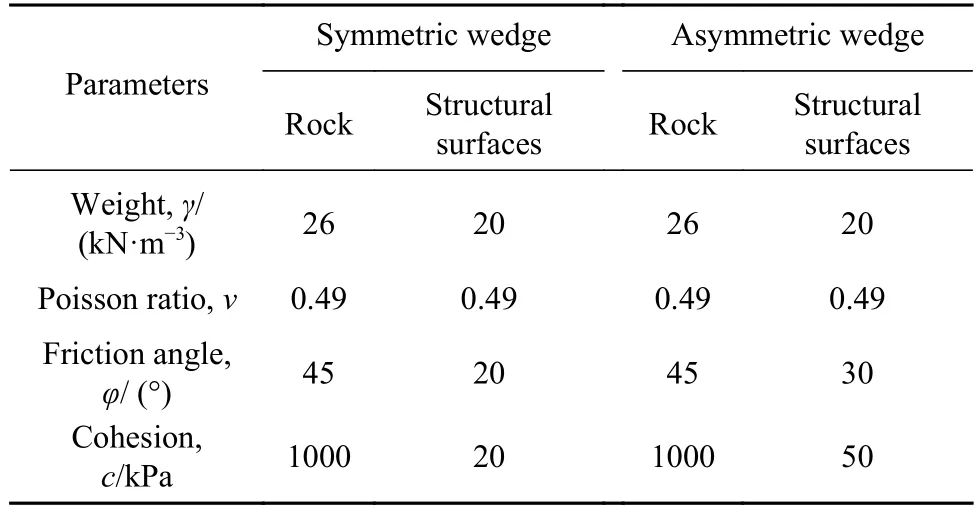
表2 算例2 的材料参数Table 2 Mechanical parameters used in example 2

表3 算例2 的几何信息Table 3 Geometric information used in example 2 (°)

5.3 讨论

从算例1 和算例2 的安全系数结果可见，对非球形滑动面采用剪应力比形式的安全系数F1较严格极限平衡法偏差较大.因为F1计算方法中默认滑动方向与非极限平衡状态下的剪应力矢量方向一致，这与严格极限平衡法的假定不同.

在本文中，虽然安全系数F2与严格极限平衡法的计算过程不同，但结果仍具有一致性.原因是：（1）本文方法计算中通过刚体假定和主滑方向的假设，预估了极限平衡状态下的滑动方向.因为采用相同的假设，所以滑动方向与极限平衡法计算得到的剪应力矢量方向一致.（2）本文方法中一点安全系数代表在滑动方向上强度的储备，整体安全系数是滑动面上各点的安全系数的中值.而极限平衡法通过对强度进行折减达到极限平衡状态得到的安全系数也代表着强度储备.

6 结语

基于滑动面唯一主滑方向计算滑动方向，通过对三维滑动面极限平衡状态的分析，将滑动面上局部安全系数定义为抗剪强度与剪应力在滑动方向上投影的比，并通过证明滑动面整体极限平衡条件，定义滑动面整体安全系数.通过与经典算例对比，验证了本文方法的可行性，并获得如下结论：

（1）本文方法安全系数定义合理，物理意义明确，计算过程简单，可以适用于任意形状滑动面，能应用于三维边坡稳定性分析中.

（2）采用剪应力比形式的三维安全系数定义没有考虑滑动方向，会错误的估计极限平衡状态的剪应力矢量方向，导致安全系数误差.本文方法考虑了滑动方向上的极限平衡状态，且滑动方向假设合理，计算结果与严格极限平衡法一致.