一类随机最优控制问题的拟蒙特卡洛方法

周洪敏 罗贤兵 叶昌伦

(贵州大学数学与统计学院,贵阳550025)

1 引言

本文考虑如下随机最优控制问题:

其中,容许控制集Λ 是L2[0,T]的一个闭凸子集；f,h,φ,g分别是关于(y,u),y,y和(y,u)的连续可微函数,且它们的导数一致有界. 在上述条件下,随机最优控制问题(1.1)-(1.2)有唯一解[1,2].

文献[3-8]给出了许多求解确定性最优控制问题的数值方法. 近年来,随机最优控制问题的数值方法得到了广泛关注.较为常用的是基于动态规划原理的方法[9,10],该方法通常需要求解对应的Hamilton-Jacobi-Bellman 方程[1,11]. 除此之外,基于随机最大值原理(SMP)的数值方法[12,13,14]也是求解随机最优控制问题的一种经典方法. 本文结合文献[15]中的基于SMP 的梯度投影优化方法进行研究.

蒙特卡洛(MC) 方法[16]是处理随机问题的一种非常重要的方法, 但收敛速度慢. 其改进的方法有很多, 如多水平蒙特卡洛方法[17,18]和拟蒙特卡洛(QMC)方法[19,20,21]. 相对于MC 方法,QMC 方法有更快的收敛速度. 为能有效地利用QMC 方法, 将(1.2) 中的Brown 运动W(t) 按Karhunen-Lo`eve(K-L)方法展开为

其中ξj～N(0,1),λj和φj(t)分别是Brown 运动对应的协方差算子的特征值和特征函数. 为使随机抽样维数和时间离散点独立,将无限维转化为有限维,对(1.3)式截断到第s项,即

本文针对随机最优控制问题(1.1)-(1.2),首先对Brown 运动按K-L 方法展开并进行截断[26],然后使用QMC 方法中的Sobol 点序列抽样,最后结合梯度投影优化算法数值求解最优控制问题,分析数值近似误差,并通过数值实验验证方法的有效性.

2 最优化系统离散近似

本节首先根据SMP 给出最优控制问题(1.1)-(1.2)的最优化系统,其次对该系统按K-L 方法展开并进行截断,然后对截断后的系统作Euler 离散,最后用QMC 方法近似梯度泛函J′(u)中的期望.

2.1 最优化系统

最优控制问题(1.1)-(1.2)的Hamilton 函数为:

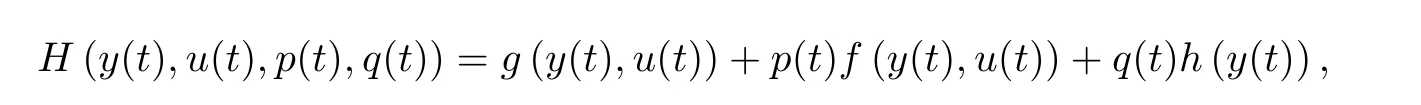
其中,耦合过程(p,q)是伴随过程对,且满足随机微分方程:

在合适的假设下,方程(2.1)有很好的适定性[15],且伴随状态p(t)满足:

2.2 Euler 离散

设{W(t)}0≤t≤T是 定 义 在 概 率 空 间(Ω,F,{Ft}t∈[0,T],P) 上 的 一 维Brown 运 动, 其 中{Ft}t∈[0,T]是由{W(t)}0≤t≤T生成的信息流.

利用(1.4),将系统(2.2)截断近似为:

2.3 QMC 近似

3 误差估计

对于系统(2.4),结合梯度投影优化方法[15],本文给出如下不动点迭代算法:

所以误差∊N主要包括K-L 截断误差,Euler 离散误差和QMC 积分误差.

为了给出后续的误差估计的证明,我们需要如下几个假设.

3.1 K-L 截断误差和Euler 离散误差

引理1 若假设1 和假设2 成立,且ˆp(t)有界,则有

3.2 QMC 误差分析

对于任意的QMC 点集P={ζ1,ζ2,··· ,ζn}和平移Δ∈[0,1]s,令P+Δ={{ζi+Δ}:i=1,2,··· ,n}是平移的QMC 点集. 定义一个权重未锚定的Sobolev 空间ϖγ,s: 对于ˆF ∈ϖγ,s,其范数定义为[21]

ˆym(·,ξ)也满足(3.10)式,其中a≲b表示a ≤Cb,C为正常数.

证明 当ν=0 时,(3.10)显然成立. 现考虑ν/=0 的情况.

首先对方程(1.2)两边同时用Leibniz 求积公式,得到

4 数值实验

本节将对一个随机最优控制问题进行数值模拟,通过数值实验验证其K-L 截断误差和QMC近似误差与理论结果的一致性.

考虑如下随机最优控制问题[15]:

4.1 K-L 截断误差

将问题(4.1)转化为如下最优化系统:

取n=210个Sobol 点,固定单个的随机平移Δ,用QMC 积分近似期望. 状态y和对偶状态p的K-L 截断误差分别如图1,图2 所示.

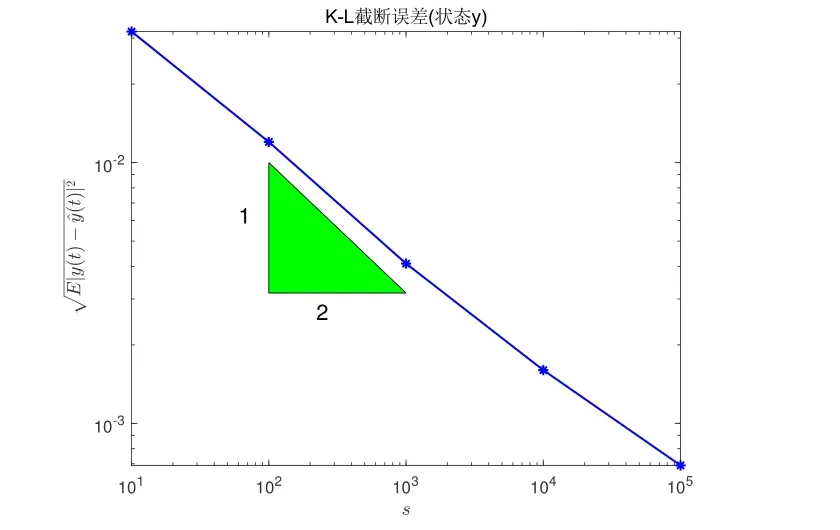
图1 状态y 的K-L 截断误差

图2 状态p 的K-L 截断误差

4.2 QMC 误差

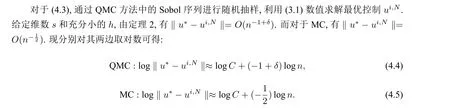
图3 MC 误差

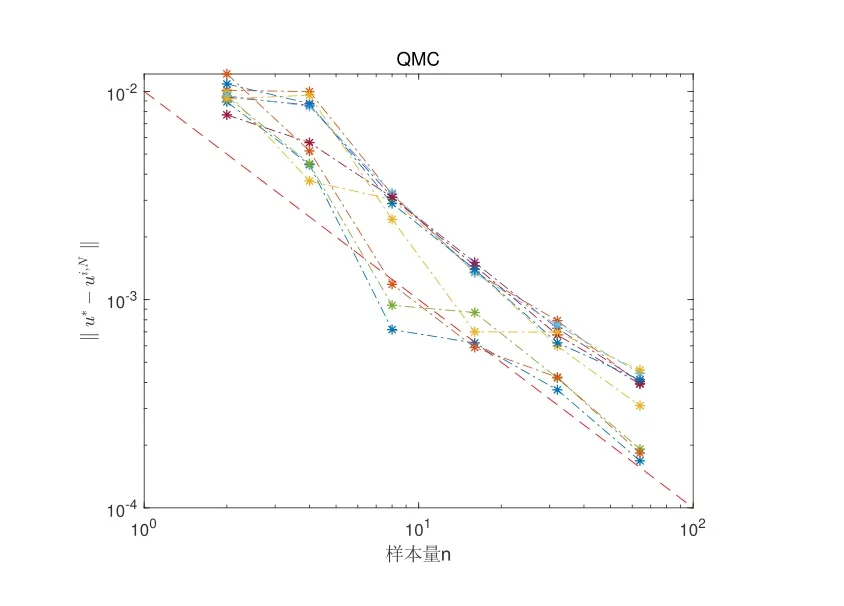
图4 QMC 误差

4.3 最优控制

从图5 可见数值解和精确解基本吻合,表明基于梯度投影优化算法的QMC 方法有效.

图5 最优控制的精确解和数值解