Blow up Solutions of the Elastic String Equation with Nonlinear Damping and Source Terms
Zhang Zaiyun Ouyang Qiancheng Zou Pengcheng Wang Qiong Ling Wenjing
(School of Mathematics,Hunan Institute of Science and Technology,Yueyang 414006,Hunan,China)
Abstract In this paper,we consider the elastic string equation with nonlinear damping and source terms. Following the ideas of Zhang and Miao [43] the blow up of the solutions with positive initial energy is investigated by the perturbed energy method.
Key words Elastic string equation Blow up Positive initial energy Perturbed energy method
1 Introduction
We consider the blow up problem for the following elastic string equation

Eq. (1.2)arises in classical mechanics,fluid dynamics and quantum field theory(see[26],[27]),and has been extensively studied. It is well known that in the casef(u) = 0,it causes finite time blow up of solution with negative initial energy(see[1]). Haraux and Zuazua obtained the global existence of Eq.(1.2)with damping termg(ut)and arbitrary initial conditions(see[2]). In[3,4],Levine studied the blow up result for solutions of Eq. (1.2)with damping termg(ut)and source termf(u)in the linear damping case (r= 0). He first introduced the concavity method and showed that solutions with negative initial energy blow up in finite time. Later, this method was improved by Kalantarov and Ladyzhenskaya [5]to more general cases. Moreover, Georgier and Todorova [6] extended Levine’s result to the nonlinear damping case(r> 0). In their work, they determined suitable relations between the nonlinearity in the damping termg(ut)and the source termf(u).More precisely,they showed that the solutions with negative energy exist globally in time ifr ≥pand blow up in finite time ifr In[33],Kirchhoff firstly proposed the so called Kirchhoff string model in the nonlinear vibration of an elastic string whereu=u(x,t) is the lateral displacement at the space coordinatexand the timet, Eis the Young modules,his the cross-section area,ρis the mass density,Lis the length,p0is the initial axial tension,δis the resistance modules andfis the external force. In fact, Eq. (1.1) is a model for the physical problem of vertical displacements of stretched elastic strings. and by using the concavity method,showed that its solutions with negative energy blow up in finite time forp>max{2q,r}.But,these solutions exist globally in time ifp ≤r.In[41],Mamadou Sango studied the blow up result for the solutions of a system of quasi-linear hyperbolic equations involving thep-Laplacian and obtained a differential inequality for a function involving some norms of the solutions which yields the finite time blow up. In the present work,we consider the elastic string equation with damping effectg(ut)and source termf(u)and establish the blow up result for this equation with positive initial energy in finite time. In this section,we use the standard Sobolev spaceLp(Ω)with the usual scalar product and norm. Lemma 3.1 Letube a solution of(1.1). Assume thatE(0) Remark 3.1 In this paper,CandCiwill denote various positive constants which may be different at different places. In this section, we prove Theorem 2.1 by the perturbed energy function method benefited from the ideas of Zhang and Miao[43]. which completes the proof of our result. The parametersρandσwere chosen in a convenient way and sufficiently large. Consequently,the authors considered a datau0with sufficiently large‖∇u0‖(large data‖u0‖∞provided thatψ ∈L∞(Rn))and obtained the blow up result. Remark 4.2 Setx=‖∇u0‖2,y=λ.It is plausible to conjecture the existence of curve(see Fig.1 as follows)Lin the plane(x,y)such that i)for any point(x,y)on the right of curveL,there are datau0,v0,such that‖∇u0‖2=xandE(u0,v0)=λ,and the corresponding solutions of(1.1)blow up in finite time(region I); ii)for any point(x,y)on the left of curveL,such a choice of data cannot be made(see region II).That is to say that in region II,solutions of(1.1)exist globally. Figure 1 The relationship between the parameters x=‖∇u0‖2 and y =E(u0,v0) Let-△be the operator defined by the triple{V,H,a(u,v)},where
2 The main result

3 Preliminary results



4 Proof of Theorem 2.1



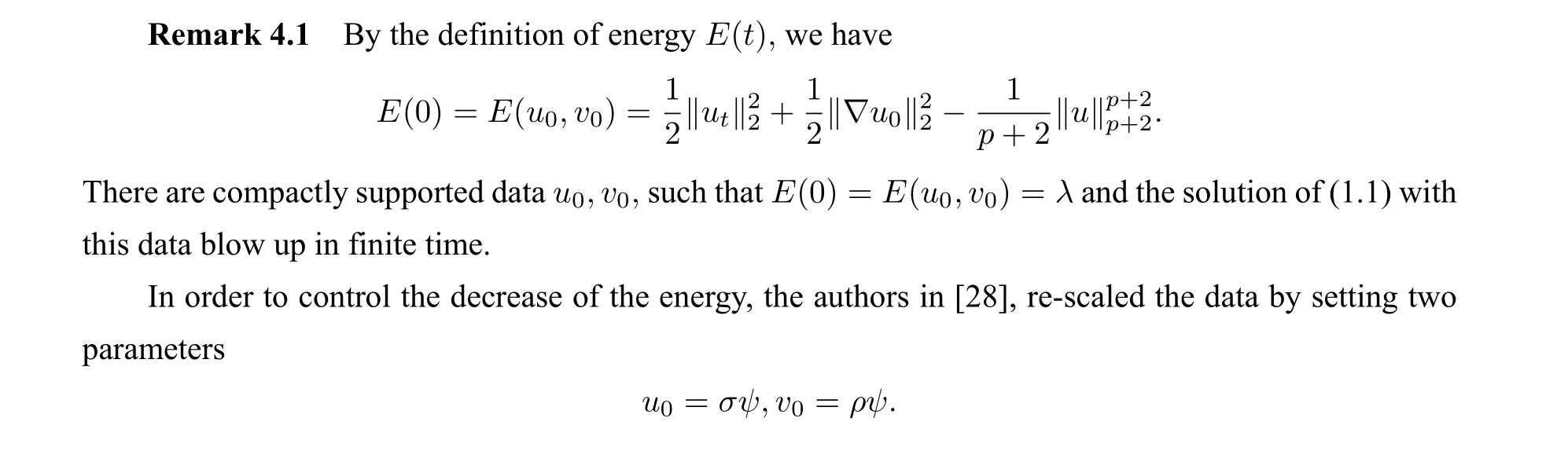

5 Further Remarks
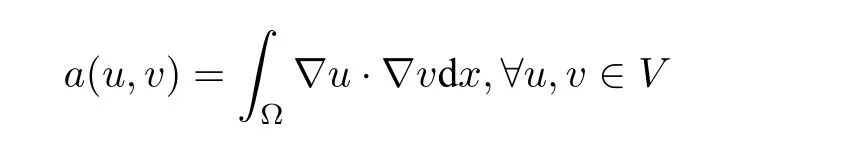

- 数学理论与应用的其它文章
- 基于AE-LSTM 改进模型的高龄人口死亡率预测
- 连续时间圆形城市模型中的进入时机与产品差异化决策
- 一类随机最优控制问题的拟蒙特卡洛方法
- On the Filtered Krylov-Like Sequence Method for Solving Non-Symmetric Eigenvalue Problems
- Almost Periodic Solutions of a Discrete Model via Quasi-uniform Asymptotic Stability
- Resource Dispatching Conditions in NFV Networks from Binding Number Perspective

