一种针对小多普勒扩展水声信道的OFDM接收算法

诸哲楠，万 磊，*，徐 锋

（1．水声通信与海洋信息技术教育部重点实验室（厦门大学），福建 厦门 361005；2．厦门大学 信息学院 信息与通信工程系，福建 厦门 361005；3.武汉第二船舶设计研究所，湖北 武汉 430064）

0 引言

随着科技的发展，人类对海洋资源的探索和开发力度逐渐加大。在此过程中，水声通信发挥着重要的作用。然而水声通信可用的带宽较小，声波仅在数千赫兹到数万赫兹范围内具有较低的传播损耗。并且水声信道物理传播特性带来了多径时延扩展与多普勒频偏扩展2个问题，造成了极具挑战性的双选择性衰落信道[1]。

正交频分复用（Orthogonal Frequency Division Multiplexing，OFDM）技术具有高频带利用率、低复杂度多径信道均衡等优点[2]。从 21世纪开始OFDM 技术逐渐成为高速水声通信最流行的选择之一[3]。然而，水声通信信道中的多普勒效应会破坏各个子载波之间严格的正交性，给 OFDM系统带来子载波间干扰（ICI）[4]。因此有效的ICI估计与均衡手段对水声OFDM 系统来说必不可少[5-8]。

针对OFDM系统所受多普勒影响大小的不同，不同的经典算法被提出来对抗子载波间干扰，恢复子载波间的正交性。当水声信道中的多普勒主要由收发端的相对运动产生时，可以近似认为信道内存在统一多普勒频偏。此时，经典的两步多普勒补偿算法可以有效地消除由多普勒频偏造成的子载波间干扰[9]。而当水声信道中存在多普勒扩展时，经过上述算法重采样后仍会残留多普勒的影响，子载波间干扰无法被完全消除。

针对双扩展水声信道，在文献[10]中，作者提出了一种渐进迭代信道估计与均衡技术，将经过信道译码后得到的数据子载波概率软信息重构为新的导频，从而等效地增加导频数目再进行信道估计，增强了OFDM 系统对多普勒扩展信道的估计能力。但该算法对于初始信道估计的准确性有一定的要求，信道译码反馈的概率软信息足够准确才能形成有效的迭代。文献[11]中，作者提出一种双向软判决反馈均衡技术，将单载波系统中的双向均衡结构引入 OFDM 系统中，缓解了串行最小均方误差（Serial MMSE）均衡器差错传播问题。相比传统单向均衡结构，该算法在复杂度增加有限的情况下获得了较好的性能增益。但该算法的前提是对信道有准确的二维估计，这本身就是一个难点问题。

事实上，除去潜艇、高速 AUV等高机动平台之外，一般水下平台的移动速度往往有限，因此造成的多普勒扩展也是有限的。本文着眼于多普勒扩展有限的信道条件，在经过针对主径多普勒的补偿之后，OFDM 系统子载波间干扰范围通常集中在邻近的几个子载波上，并且子载波间干扰项（多普勒矩阵中的元素）随着子载波索引变化缓慢。此外，由于实际水声信道中多径通常成簇出现，每簇的特征径与水体折射、水面水底的反射有关[1，12-13]，因此本文采用簇稀疏水声信道模型。

基于以上2点，本文提出了一种基于多项式拟合的水声 OFDM接收算法。本算法充分利用多普勒扩展有限、以及簇稀疏的水声信道的特点，近似认为每簇内的多普勒频偏相等[13]，将其对应的子载波间干扰项（多普勒矩阵元素）近似为多项式函数，通过连续导频对多项式系数进行初始化，并将均衡得到的数据子载波作为新的导频，迭代进行多项式拟合和数据符号频域均衡。本算法分簇处理的思路有效地减少了所需估计的多项式系数的个数，从而降低了计算复杂度，仅需信道的分簇先验信息和信道的一维（时延）估计，无需二维估计即可取得较好的性能。

1 系统模型

本文采用带循环前缀（Cyclic Prefix，CP）的OFDM（CP-OFDM）系统。CP-OFDM符号时长为T，子载波数目为N，带宽为B，系统中心频率为fc。经过针对主径多普勒频偏的补偿后，具有L条多径的时变水声稀疏信道可等效表示为

式中：第l条多径对应的幅度为lA；时延为lτ；多普勒因子为al。

经过以上信道，在接收端去除循环前缀 CP、进行FFT解调后的CP-OFDM接收信号可表示为

式中：z为接收符号向量；s为发送符号向量；w为噪声向量；lξ为每径的复增益；k、m为子载波索引。

在有限多普勒扩展信道中，多普勒因子al较小，从而子载波间干扰范围较为有限。因此，多普勒矩阵Γl可以近似认为是带限矩阵，等效信道矩阵H也是带限的。假设该带限矩阵的单边宽度（多普勒深度）为D，由式（2）可得

因此，可以认为每个子载波的ICI主要来自于2D个相邻的子载波，信道矩阵H仅在主对角线和主对角线附近的2D个次对角线处有非零值。多普勒深度D的取值可以权衡信道均衡的性能和计算复杂度。

2 基于多项式拟合的接收算法

2.1 多项式拟合

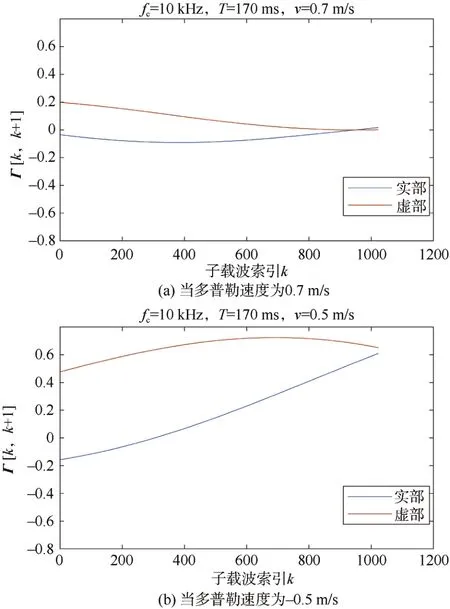
图1 子载波间干扰项Γ[k, k+1]变化情况Fig.1 Variations of disturbance item between subcarriers Γ[k, k+1]

2.2 多项式系数求解

本文所提算法采用如图2所示的OFDM 导频设计，将连续导频与均匀导频相结合，设起始连续导频的长度为Nt，均匀导频间隔为Nd。

图2 导频设计Fig.2 Pilot design

2.3 频域均衡和多项式系数更新

本文所提算法迭代进行频域均衡和多项式系数更新，算法流程图如图3，具体流程如下。

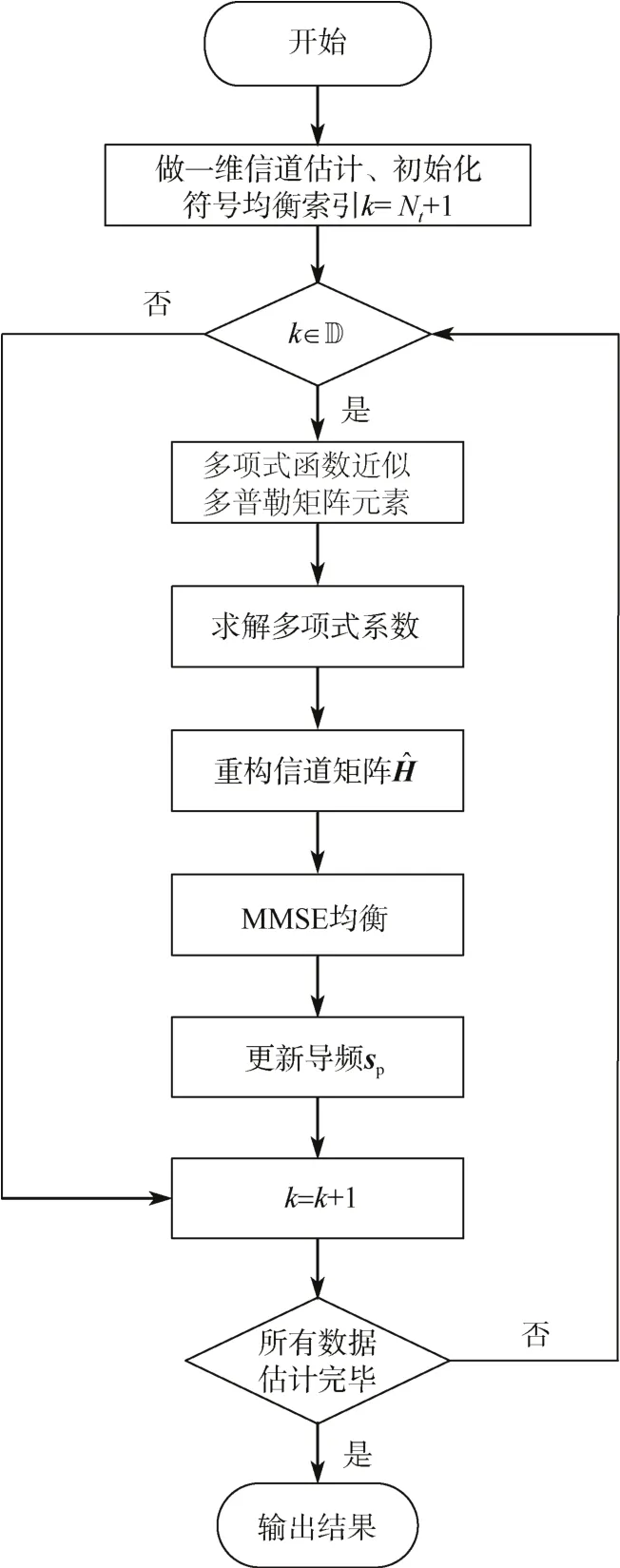
图3 算法流程图Fig.3 Algorithm flow chart

2.4 信道分簇先验信息

通常在水声 OFDM信号传输之前会发送一段线性调频信号来探测信道，通过接收线性调频信号与本地信号的相关粗略地估计信道多径时延。借助线性调频信号，使用K-means[15-16]等算法即可得到信道时延分布区域等先验信息。

3 仿真分析

为了说明本算法的可行性，本文在水声多径信道环境下进行了仿真分析。仿真采用的CP-OFDM系统总子载波数N= 1 024，符号时长T= 1 70.7ms，循环前缀长度Tcp=43 ms，带宽B=6 kHz，中心频率fc=10 kHz，连续导频长度Nt= 1 28，均匀导频间隔Nd= 4 ，数据子载波总数Kd= 6 72。

仿真采用如图4所示的多径信道。信道中特征径由Bellhop[17]在浅海环境设定下产生，收发端均处于40 m深度，相距1 km，海水深度100 m。信道中簇内的其余多径时延服从高斯分布。假设收发端水平匀速相对运动，相对速度3 m/s，在针对主径的多普勒补偿后，簇内多普勒因子取aC1= 0 ，aC2= 8 .82e - 5，aC3= 1 .18e- 4 。

图4 仿真多簇信道Fig.4 Simulated clustered channel

图5为本文所提算法与一维、二维估计均衡方法的误比特率仿真对比结果。其中，信道编码使用码率为1/2的LDPC码，数据符号采用16正交幅度调制（16-QAM），符号平均能量Es=1。一维信道估计使用正交匹配追踪（OMP）算法实现。本文所提算法多项式阶数选择n=2，多普勒深度取D= 3 。基于本文算法相同的导频分布，二维估计均衡使用二维OMP估计得信道矩阵后，使用同样的D=3的串行最小均方误差方法进行均衡。

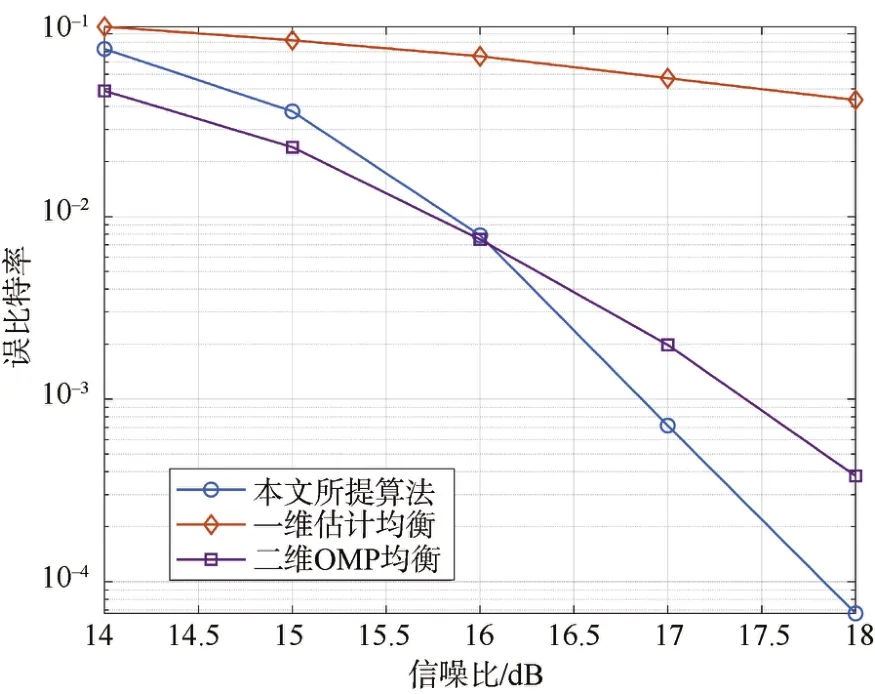
图5 仿真误比特率Fig.5 Simulated BER

由图5仿真结果可知，本文基于多项式拟合的接收算法相比基于相同导频数量的传统一维信道估计均衡方法取得了明显更优的性能。相比二维估计均衡方法，在信噪比小于16 dB时，本文算法由于一维信道估计、多项式拟合误差导致的差错传播等问题，性能弱于传统的二维估计均衡方法。当信噪比高于16 dB时，本算法能很好地追踪多普勒矩阵元素的变化，迭代进行频域均衡和多项式系数更新，性能比传统二维估计均衡方法更优。

4 结束语

在水声双扩展信道条件下，为了对抗子载波间干扰，传统方法需要对信道进行复杂的二维估计。针对有限多普勒扩展的信道条件，本文提出的基于多项式拟合的接收算法充分利用信道先验信息，用多项式函数近似多普勒矩阵元素变化，仅需一维估计即可实现较好的性能。仿真结果显示，本算法能有效对抗子载波间干扰，相比相同导频数量的一维估计均衡方法性能增益明显。相比二维的方法，本算法在高信噪比条件下性能更加优异。未来将考虑在海洋环境进行现场实验以进一步验证该算法的性能。