航行体近水面航行附加质量与阻尼的数值研究

邱绪明，柯贵喜，路 伟，江兴隆

（1.中国船舶集团有限公司第七一〇研究所，湖北 宜昌 443003；2.清江创新中心，湖北 武汉 430076）

0 引言

近水面无人有动力自航式航行体是一种先进的海洋工程装备，研究其运动特性具有很高的工程实用价值。航行体在工作中会频繁地产生横摇、纵摇运动，其摇荡的周期与幅值会影响其工作的稳定性，一旦其摇荡幅值超过标准范围，航行体很容易出现难以控制的偏航与失稳现象[1-3]。其运动的状态主要取决于工作环境条件和自身运动特性，而在描述其在水中运动特性的运动方程中，附加质量及阻尼是2个关键参数[4-7]。

本文针对横摇、纵摇运动受粘性作用较大的特点对这2种运动状态进行研究，运用STAR-CCM+软件，建立了带兴波自由面的数值水池。在粘性流环境下模拟航行体在阻尼作用下的自由横摇和纵摇的衰减过程，得到航行体在水中横摇与纵摇的固有周期，根据公式计算出航行体在空气中的自由横摇和纵摇周期。航行体在空气与水中运动的周期之差是由水的附加质量引起的，可以根据周期之差计算出横摇和纵摇的附加质量，航行体在水中运动横摇和纵摇的幅值衰减是由水阻尼产生的能量耗散。本文采用峰值处理法计算出航行体横摇和纵摇的对数衰减率以及阻尼系数[8-9]。

1 仿真基础条件

1.1 模型参数

选取航行体简化模型作为仿真对象，与原模比例为1∶1，航行体主尺度参数如表1所示。

表1 航行体主尺度参数Table 1 Main parameters of underwater vehicle

航行体的网格模型及其坐标轴对应方位如图1所示。

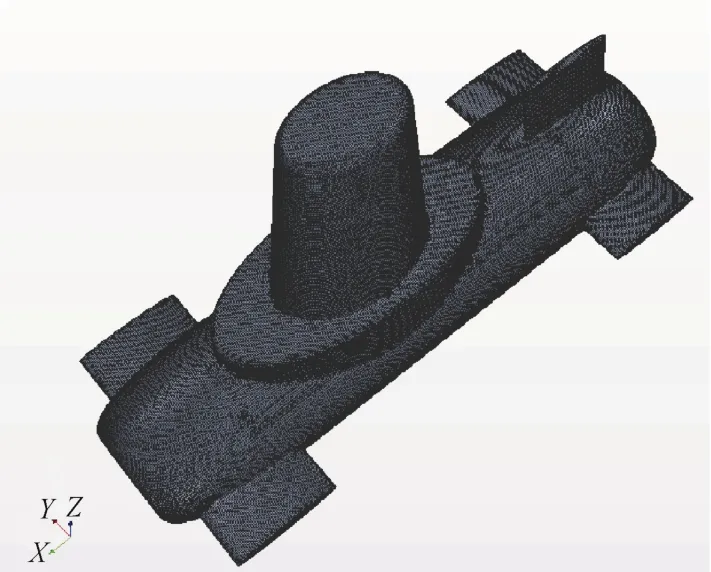
图1 航行体网格模型Fig.1 Mesh model of underwater vehicle

1.2 计算域处理

将整个数值水池分为内域和外域，内域刚好包含整个航行体，外域范围大致为-3Lx＜x＜3Lx，-9Ly＜y＜9Ly，-2Lz＜z＜2Lz，其中Lx、Ly、Lz分别为航行体自身的长、宽、高尺度。如图2所示，中间的内域为动网格区域，外部则为静态网格区域，当物体运动时，动网格区域随其同步运动。

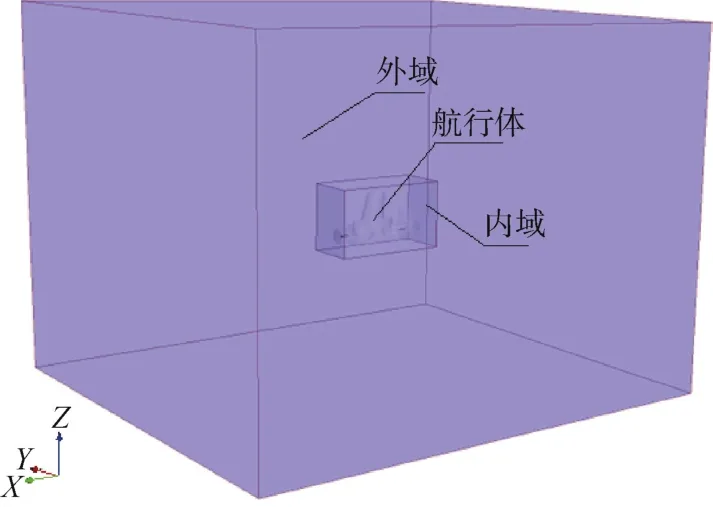
图2 三维数值水池空间划分Fig.2 Spatial division of three-dimensional numerical wave tank

动网格区域需要采用重叠网格方法。重叠网格由背景网格和部件网格相互重叠组成。各网格区域在空间上重叠，但不存在连通关系，各区域分别独立采用离散控制方程进行隐式不定常求解，并通过边界点的插值和数据传递来实现区域连通，最终得到整个计算域的流场信息[10-11]。

本文采用流体体积方法（Volume of Fluid，VOF）建立了兴波自由面，使用六自由度运动求解器DFBI和重叠网格技术求解航行体运动，并对波面大致区域和重叠区域内的网格进行了加密处理，处理后的网格截面如图3所示。

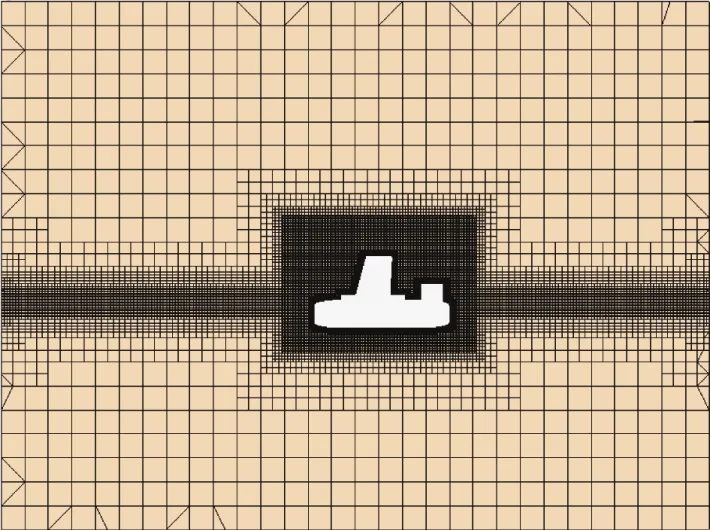
图3 数值水池网格截面Fig.3 Grid section of numerical wave tank

2 计算原理

STAR-CCM+针对不可压缩粘性流体，在整个计算域内运动规律采用连续性方程和 N-S方程作为控制方程：

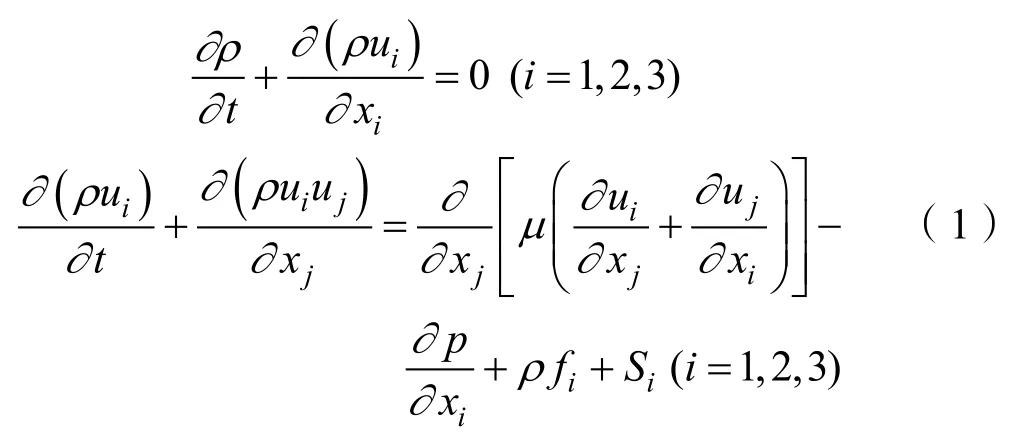
式中：ρ为流体密度；μ为流体黏度；p为静压；fi为单位质量力；ui、uj为时均化后的速度分量。

本文采用隐式非定常计算，在每个时间步长对计算域内流场进行控制方程的求解，然后对航行体表面进行积分以获取当前时刻的航行体受到的横摇或纵摇力矩[9]。以横摇为例，取三维右手直角坐标系，航行体前进方向为x轴，水平运动方向为y轴，垂直水平面方向为z轴，其表达式为

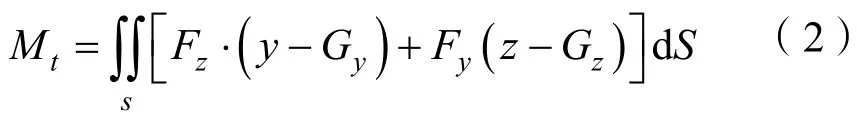
式中：Fz、Fy分别为对应网格位置处流场作用于航行体表面的水动力作用力在z轴与y轴方向的分量；Gy、Gz分别为航行体重心在y、z轴的坐标，显然，当坐标原点取为航行体重心时，Gy、Gz均等于0。

由航行体所受的横摇力矩Mt及其横摇惯性矩与横摇附加惯性矩Jxx、ΔJxx求解出航行体的横摇角加速度，并进一步迭代求解出横摇角速度θ˙t以及横摇角度θt等运动信息，计算表达式如下：

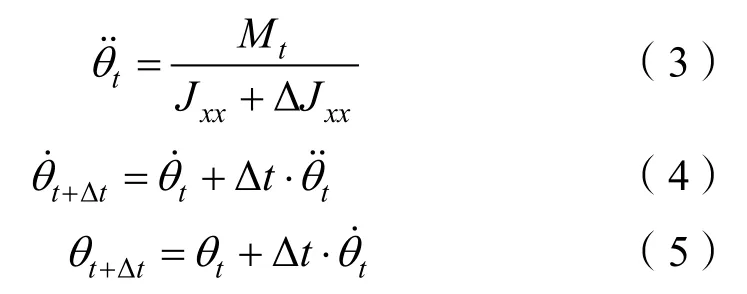
根据迭代求解出的下一步运动参数信息，返回给求解器结合重叠网格技术对航行体的运动状态进行更新，选取合适的时间步长，在每个时间步长内重新以上迭代计算过程，即可准确地模拟航行体的横摇自由衰减运动，纵摇自由衰减运动求解过程与之同理。

3 仿真与数据处理

本文分别给定15°、10°、5°的初始横摇、纵摇角度，释放航行体自由运动，计算至适当时长，计算结果如图4-9所示。

图4 初始横摇角15°自由衰减曲线Fig.4 Free attenuation curve with initial roll angle of 15°

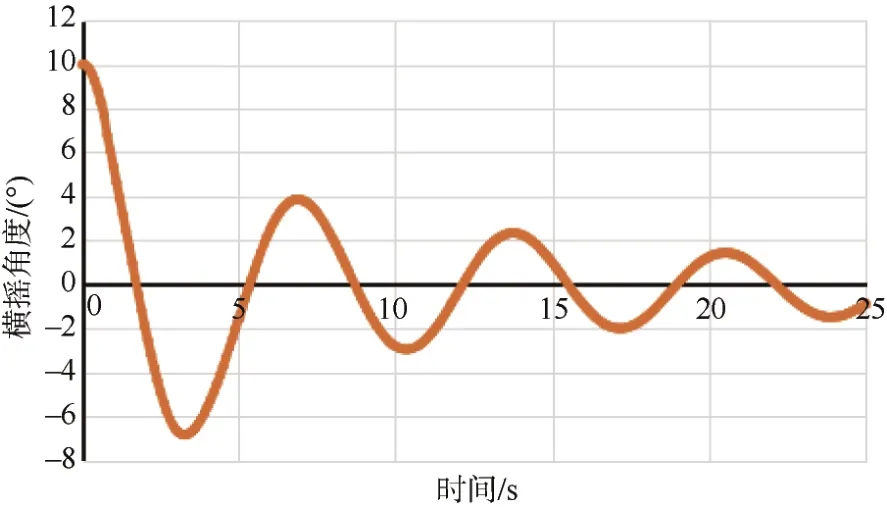
图5 初始横摇角10°自由衰减曲线Fig.5 Free attenuation curve with initial roll angle of 10 °

图6 初始横摇角5°自由衰减曲线Fig.6 Free attenuation curve with initial roll angle of 5 °

图7 初始纵摇角15°自由衰减曲线Fig.7 Free attenuation curve with initial pitch angle of 15 °

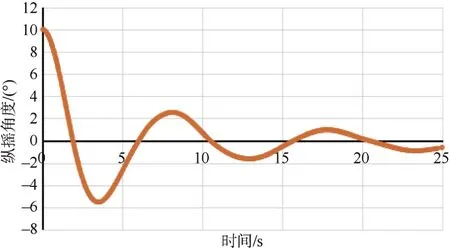
图8 初始纵摇角10°自由衰减曲线Fig.8 Free attenuation curve with initial pitch angle of 10 °

图9 初始纵摇角5°自由衰减曲线Fig.9 Free attenuation curve with initial pitch angle of 5 °

本次CFD仿真目的是得到航行体的横摇与纵摇的附加质量与阻尼系数，但仿真直接得到的结果只有横摇与纵摇的自由衰减曲线，因此本文对附加质量与阻尼系数的计算过程进行说明。

3.1 附加质量计算

附加质量与能量辐射无关，它是由物体运动引起的周围流场中流体的惯性运动所致，当航行体作简谐摇荡时，在半个加速周期中因物体运动而积聚在流体中的能量（指与辐射能量无关的那一部分能量）在接下来半个减速周期中又全部还给了物体。

以横摇为例，航行体自由横摇运动时，作用于航行体上有惯性力矩和恢复力矩[12]，其表达式如下：

式中：Mxx、Cxx分别为航行体受到的惯性力矩与恢复力矩；Jxx、ΔJxx分别为航行体的横摇惯性矩与横摇附加惯性矩；D为航行体自身重量；h为航行体的稳心高，即航行体的重心与浮心的垂向距离。

根据动平衡原理，航行体在自由横摇运动状态下任意瞬时惯性力矩与恢复力矩大小相等，方向相反，则

由该运动方程求解得出

本文中，航行体自身重量D、横摇惯性矩Jxx、横摇惯性矩ΔJxx、稳心高h为已知量，固有周期可以通过仿真得到的自由横摇衰减曲线得出，因而可依据式9得到航行体的横摇附加惯性矩。

观察横摇仿真结果图4-6，可以发现横摇周期基本保持不变，随着横摇初始角度的减小，横摇周期仅有不明显的缩短。

参考横摇周期受阻尼影响的公式

式中：Tθ1为阻尼影响下的横摇周期；v为液体的运动粘度。由式10可以看出，横摇阻尼使横摇周期稍有增大，但是作用甚小，以至于可以忽略不计。理论上当横摇初始角度减小时，横摇阻尼大幅减小，因而横摇周期会有不明显的缩短。仿真结果的该项特征符合理论预期。

航行体纵摇附加惯性矩的计算过程与横摇同理，而观察纵摇仿真结果图7-9，却发现当纵摇角度较大时，纵摇周期大幅缩短，且在初始纵摇角度为10°和15°时均出现该现象。

本文结合模型特征分析，纵摇角度超过一定程度时，航行体有较大部分体积位于水面以上，形成“出水”现象，与其正常工作形态有较大差异。在“出水”形态下，航行体纵摇运动所能带动的流域内随其作惯性运动的流体质量大幅减少，即纵摇附加惯性矩ΔJyy大幅减小。根据式9，纵摇的固有周期Tθ会随ΔJyy大幅减小而大幅缩短。因此，本文统计纵摇周期时不考虑“出水”状态下的数据，仅统计纵摇幅值大幅衰减后的纵摇周期。

统计图4-9的横摇与纵摇运动周期并取均值，得到航行体的横摇固有周期为 6.8 s，纵摇固有周期为11.4 s。代入其他参数，由式9可以得到航行体的横摇、纵摇附加惯性矩分别为15 873 kg·m2和36 120 kg·m2。

3.2 阻尼系数计算

由于实际上水是有粘性的，航行体会受到水的非线性阻尼作用，因此以横摇为例，航行体在静水中的非线性横摇运动方程为[13]

式中，B1、B2分别为航行体非线性横摇运动中的线性、非线性阻尼系数。该方程适用于较大角度的横摇运动，而本文中考虑较小的航行体的横摇角度，因此可以简化为线性横摇运动，其运动方程为

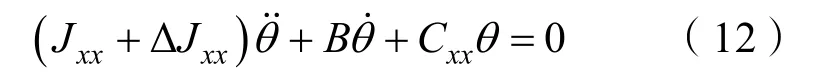
式中，B为航行体线性横摇运动中的线性阻尼系数，理论上小角度横摇运动时线性阻尼系数B保持不变。

对横摇衰减曲线图4-6采用峰值处理法，将自由横摇衰减曲线上的横摇角相对于平衡位置的幅值按照正负分为2组横摇峰值角度θ1、θ2、…、θn，根据2个相邻的横摇峰值角度θi、θi+1可以算出横摇对数衰减率

将一组横摇峰值角度所有相邻数值分别代入求出横摇对数衰减率，再取平均值，即

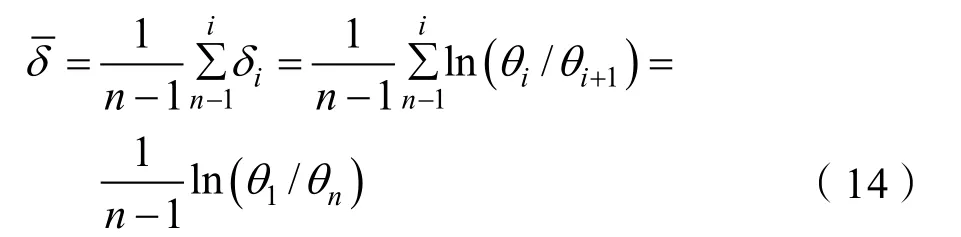
由式（14）可以得到航行体横摇对数衰减率。

航行体横摇无因次衰减系数为

航行体横摇线性阻尼系数为

依据式（16）代入已知量便可得到航行体的横摇线性阻尼系数。

分别统计并处理图 4-6的横摇运动仿真数据，得到初始横摇角分别为15°、10°、5°时，航行体的横摇线性阻尼系数分别为 221.909（N·m）/（（°）/s），201.766（N·m）/（（°）/s），191.374（N·m）/（（°）/s）。可以看出，随着航行体初始横摇角的增大，横摇线性阻尼系数有一定程度的增大，这与小角度横摇状态下的线性阻尼系数保持不变的理论预期不相符。

本文结合航行体水下运动的特点进行分析，产生这种现象的原因在于航行体横摇运动的阻尼主要成分是漩涡阻尼，漩涡阻尼的阻尼系数大小与横摇幅值一般近似呈平方关系，所以航行体在小角度横摇时也不会保持恒定的线性阻尼系数。

同理可对图 7-9纵摇运动仿真数据采用峰值处理法，得到初始纵摇角分别为15°、10°、5°时，航行体的纵摇线性阻尼系数分别为 385.666 （N·m）/（（°）/s），372.151 （N·m）/（（°）/s），257.381 （N·m）/（（°）/s）。可以看出，当初始纵摇角超过一定程度时，纵摇线性阻尼系数存在突变，纵摇衰减速度大幅增加。

这种现象可以结合航行体模型结构特征进行分析。当初始纵摇角超过一定程度时，航行体如前述有“出水”现象，此时其纵摇运动会造成水线面的剧烈变化，而这个水线面的变化过程由于要克服水的表面张力，会产生大量的能量耗散，因此会出现纵摇线性阻尼系数的突变。当纵摇幅值没有超过这个程度，例如图 9初始纵摇角为 5°时，纵摇幅值衰减特征与横摇相类似，说明此时纵摇运动阻尼的主要成分也是漩涡阻尼，阻尼系数大小与纵摇阻尼近似呈平方关系。

4 结束语

本文运用STAR-CCM+软件，在粘性环境下对航行体受粘性影响较大的横摇与纵摇 2种运动进行了仿真，并采用重叠网格与VOF波方法保证了仿真结果的严谨性。根据粘流仿真结果计算得到相应自由度运动时的附加质量与线性阻尼系数，对比初始角度分别为15°、10°、5°时自由衰减运动的特征，得出了阻尼系数随初始角度的变化特性，并分析了纵摇“出水”运动状态对附加质量与阻尼系数的影响。