基于RBF-MPC的水下机器人避碰控制

李 晨，代 笠

（1.海军装备部驻宜昌地区军事代表局，湖北 宜昌 443003；2.海军装备部驻广州地区军事代表局，广东 广州 510000）

0 引言

水下机器人作为重要的海洋装备，被广泛应用于资源勘测、海洋工程、水下救助以及侦察打击等军民领域多种场景。为了在复杂多变的海洋环境中顺利完成使命任务，水下机器人需要能够结合自身运动特性，以及周围暗礁、锚链等危险障碍物信息，基于路径跟踪实现有效的避碰控制。

国内外围绕水下机器人路径跟踪控制问题开展了广泛研究，早期研究采用比例-积分-微分控制实现水下机器人运动控制和路径跟踪[1]。由于水下机器人运动具有强非线性，并且会受到复杂的外部环境干扰，该类方法往往效果有限。文献[2]-[4]将滑模控制等方法引入路径跟踪控制，以改善传统算法的稳定性和收敛性，但在避碰控制场景下缺乏对外部环境与执行机构等约束进行处理的有效手段。

模型预测控制（Model Predictive Control，MPC）具有能够显式处理系统约束的优势。文献[5]构建了MPC控制函数，降低无人潜航器轨迹跟踪控制的能耗，同时减小跟踪误差保证跟踪精确性。文献[6]开发了基于Lyapunov的 MPC框架，提高了无人潜航器的轨迹跟踪精度。这些研究基本直接采用传统动力学模型作为预测模型，在模型误差修正方面考虑有所欠缺。

有研究者进一步将神经网络引入控制器，文献[7]通过神经网络估计水动力阻尼过程的逼近误差，从而提升了控制器对模型不确定项的控制能力。文献[8]利用递归神经网络的动态特性辨识系统，简化了仅辨识未知非线性函数带来的控制器设计复杂性。文献[9]改进Elman网络作为预测模型，提出并推导了用于求解预测控制律的灵敏度导数公式，用于水下机器人神经广义预测控制。

因此，本文提出了一种水下机器人避碰控制方法，以引入约束条件的MPC算法为基础，采用径向基函数（Radial Basis Function，RBF）神经网络修正传统动力学预测模型，对水平面避碰规划路径进行跟踪控制。通过仿真试验证明了该方法能够在避碰场景下实现有效的路径跟踪控制，并且相比传统MPC方法控制精度有所提升。

1 基于RBF神经网络修正的预测模型

本文以水下机器人水平面运动作为分析对象，仅考虑纵向运动、横向运动与偏航运动 3个自由度。取惯性坐标系与载体坐标系下状态向量分别为[x,y,ψ]T与 [u,v,r]T，则运动学方程为

式中：x为前向位移；y为侧向位移；ψ为航向角；u为前向速度；v为侧向速度；r为航向角速度。

动力学方程为

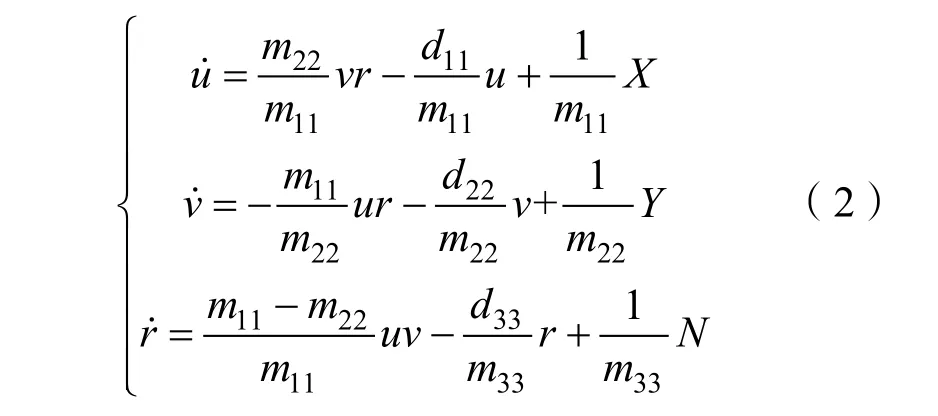
式中：m11、m22与m33为惯性矩阵元素；d11、d22与d33为水动力阻尼矩阵元素；X、Y与N分别为前向作用力、横向作用力与偏航力矩。

根据式（1）与式（2）建立基础动力学预测模型，考虑到该预测模型建模误差，采用 RBF神经网络建立误差补偿函数。RBF神经网络作为一种单隐层前馈网络，由输入层、隐藏层、输出层3层网络结构组成，具有较好的非线性函数的逼近功能，并且有利于降低水下机器人控制器的实时运算负担[10-11]。本文采用9输入3输出RBF神经网络结构建立误差补偿函数。

输入层向量xi由状态测量值、执行机构作用力与状态预测值3部分组成，具体定义为

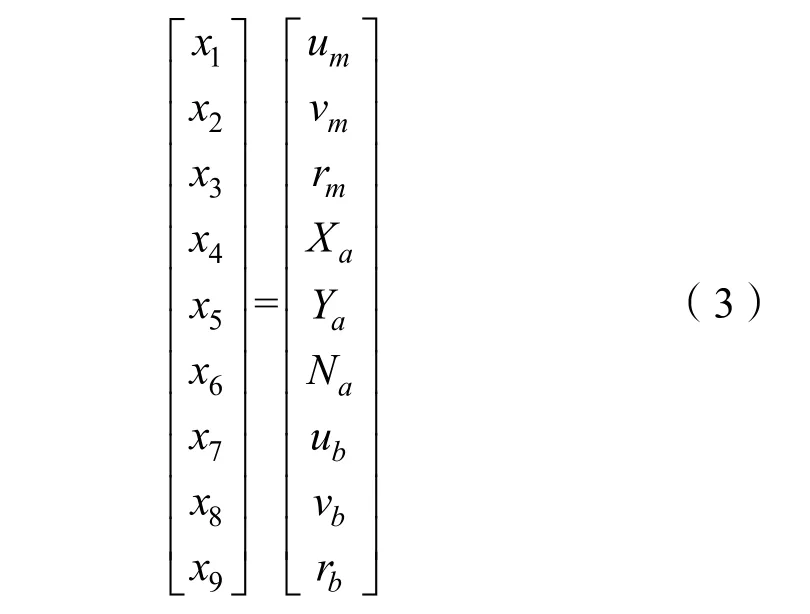
式中：um、vm与rm分别为前向速度、侧向速度与航向角速度的状态测量值；Xa、Ya与Na分别为执行机构产生的前向力、横向力与偏航力矩；ub、vb与rb分别为基础动力学模型输出的前向速度、侧向速度与航向角速度状态预测值。

通过将神经网络补偿的动力学模型作为 MPC预测模型，使预测模型更加逼近真实载体的动力学响应特征，从而提升基于 MPC的路径跟踪控制效果。

2 基于MPC的水下机器人避碰控制

3 仿真实验

为验证基于RBF-MPC的水下机器人避碰控制算法，在MATLAB下开展运动控制仿真试验，基于某型自研产品数值仿真设置动力学模型参数，具体如下表所示。

表1 动力学模型参数表Table 1 Dynamic model parameters

采用传统MPC与RBF-MFC 2种算法对预设的全局避碰规划路径进行跟踪控制，其中传统MPC直接以动力学模型作为预测模型，RBF-MFC采用离线训练神经网络修正后动力学模型作为预测模型。设定初始艏向角为0，初始坐标为原点，水下机器人水平面避碰运动过程如图1-6所示。

图1 航行轨迹图Fig.1 Trajectory graph

图2 路径跟踪误差曲线图Fig.2 Curve graph of path tracking error

图3 前向速度曲线图Fig.3 Curve graph of forward velocity

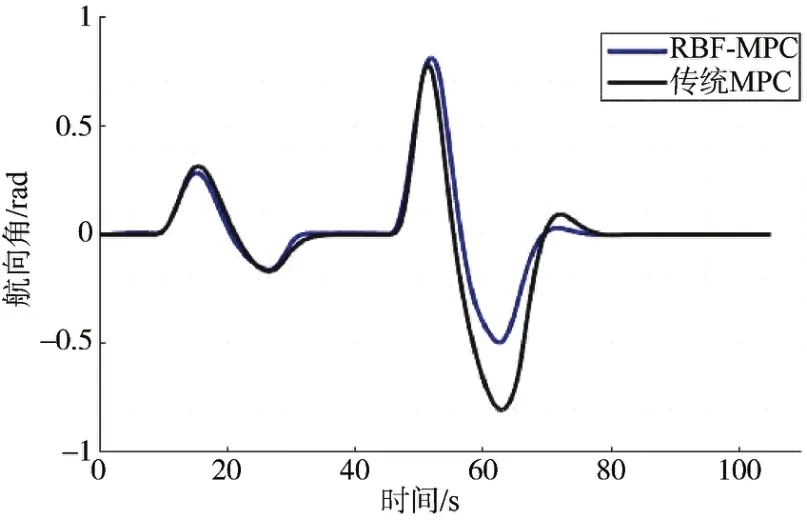
图4 航向角曲线图Fig.4 Curve graph of heading angle

图5 前向推力曲线图Fig.5 Curve graph of forward thrust

图6 转艏力矩曲线图Fig.6 Curve graph of turn stem torque

根据避碰航行轨迹可初步看出，2种方法均可控制水下机器人跟踪避碰规划路径，先后左偏约5 m与12.5 m，依次避开2个障碍物。

进一步分析避碰路径跟踪误差，传统MPC控制算法的均值为0.033 m，标准差为0.51 m，2次避碰最大值分别达到0.75 m与2.7 m；RBF-MPC控制算法的均值为0.006 m，标准差为0.17 m，2次避碰最大值分别为0.09 m与0.6 m，在平滑度与精确性方面的控制效果均有所提升。

4 结束语

本文针对水下机器人避碰场景下的路径跟踪控制问题，设计了一种RBF-MPC控制方法。通过RBF神经网络补偿传统动力学模型的建模误差，提高了预测控制模型精度。在滚动优化环节显式考虑外部环境、执行机构等约束条件，求解避障路径的跟踪控制量。仿真结果证明该方法能够有效控制水下机器人跟踪避碰路径规避障碍物，并且相比于传统MPC控制方法路径跟踪误差更小。