基于残余自干扰获取的带内全双工水声通信系统结构方案与仿真

赵云江，张小华

（1.中国船舶集团有限公司第七一〇研究所，湖北 宜昌 443003；2.清江创新中心，湖北 武汉 430076）

0 引言

带内全双工（In-Band Full-Duplex，IBFD）[1-5]水声（Underwater Acoustic，UWA）通信技术可同时发射和接收相同频带内的通信信号，可显著提升频率利用效率，在水声信道可用频谱资源严重受限的背景下具有着重要的研究意义与应用价值。而实现 IBFD-UWA通信技术过程中需要对本地近端发射端发射的强自干扰（Self-Interference，SI）进行抵消，进而使近端接收端可顺利接收并解调远端弱期望信号，因此，如何实现本地强 SI信号的抑制与抵消，是需要解决的关键性问题。

目前，针对IBFD通信实现过程中的自干扰抵消（Self-Interference Cancellation，SIC）的过程可主要总结为以下几个步骤：1）空间域SI抑制[6-8]；2）SI复杂传播信道建模[9-13]；3）模拟域SIC[14-16]；4）数字域SIC[17-19]。其中，空间域SI抑制可显著降低后续模拟域及数字域SIC压力，但同时部分研究结果[20]表明，空间域上的主动及被动SI抑制会影响 SI传播信道，进一步加剧了频率选择性衰落效应。

为了实现SIC，需对SI信号进行较为精准的传播信道估计，以得到信道抽头及时延从而结合本地参考信号进行SI信号的重构，进而通过减法器实现抵消。从已公开论文统计及研究经验来看[9-13，19]，为了能够达到良好抵消效果（大于60 dB的自干扰抵消），需要对相对主径幅度达到10-3～10-4的信道抽头进行精准的估计与抵消。文献[21]对IBFD- UWA通信系统在实际应用环境下的 SI传播信道进行了简化建模与仿真，给出了对不同 SI传播信道抽头个数抵消后的残余干扰仿真结果，在对信道的 10个抽头进行抵消后，残余干扰仍然高于接收机的噪声下限。文献[13]考虑到在实际应用中，水声通信机壳体对自干扰传播信道的影响，建立了基于工程样机实物的有限元简化模型，并通过仿真和实验证实了实际工程应用状态下 SI主要由环路自干扰（Self-Loop Interference，SLI）及多径自干扰（Self-Multipath Interference，SMI）构成，SI成分的多样性造成了 SI传播信道极其复杂，使得传统半双工UWA通信过程中的稀疏信道估计方法[22-23]在IBFD-UWA通信系统中的应用受到了限制。

SI信号构成可主要分为3类，即线性分量、非线性分量[24]及发射机噪声[25]。其中线性分量是 SI信号中能量占比最大的部分，而非线性分量主要由带内全双工通信系统中的功率放大器（Power Amplifier，PA）引入，若不对此分量进行抵消，将会影响系统整体SIC效果。针对PA引入的非线性失真分量的抵消已有部分研究结果，主要由非线性重构[16，18]、辅助链路[19]、预失真补偿[26]等方式实现，但独立模拟域或数字域的SIC方案性能有限[1]，且若模拟干扰抵消效果过好，会导致数字干扰抵消性能的下降。这种结果主要由2个方面原因造成：其一，残余信号的能量已经过低，导致残余 SI信道估计结果不准确；其二，残余信号与参考信号已存在较大差异，以参考信号进行残余干扰信号信道建模无法得到精准的信道估计结果。

基于上述内容，本文基于前期研究工作基础，提出了一种基于残余自干扰获取（Residual Self-Interference Acquisition，RSIA）的IBFD M元扩频UWA通信方案以解决上述问题，具体包括：

1）对文献[16]及文献[19]中的核心思想进行融合以完成初步模拟域SIC；

2）通过RSIA系统结构（如图1所示）获取精准的残余干扰信号进而解决残余信号与参考信号存在较大差异的问题，通过联合模拟域与数字域共同实现IBFD M元扩频UWA通信过程。

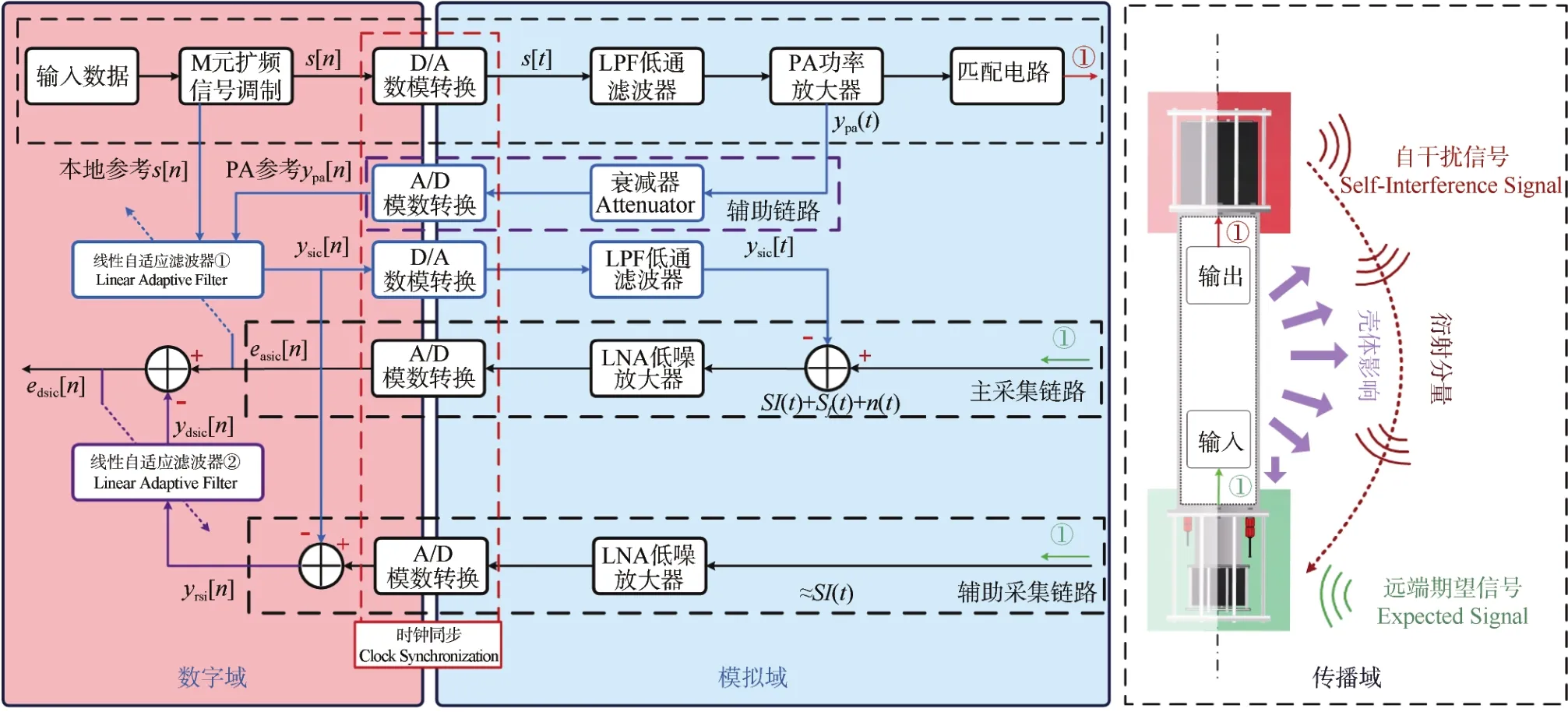
图1 基于RSIA的IBFD-UWA通信系统结构设计方案Fig.1 Structural design scheme of IBFD-UWA communication system based on RSIA

综上，本文的各节内容安排如下：第1节中通过计算得到了实现IBFD-UWA通信所需的SIC需求；本文提出的基于RSIA的IBFD-UWA通信系统结构模型在第2节中进行详细介绍；第3节中对所提出的RSIA系统结构模型进行仿真分析；最后在第3节中总结全文并指出后续研究工作方向。

1 IBFD-UWA通信系统自干扰抵消需求分析

基于前期研究结果，可将到达近端接收端的SLI能量作为需要抵消的SI能量上限，以环境噪声级作为抵消效果的上限，并通过被动声呐方程的变形来描述强 SI信号、远端期望信号、传播损失能量关系，具体如式（1）所示。

式中：SL为发射声源级；TL为传播损失；NL为环境噪声级；DI为接收阵的接收指向性指数；Rs为接收端的远端期望信号的信干噪比（Signal to Interference Noise Ratio，SINR）。其中，传播损失由文献[27]所述方法求得，假设IBFD-UWA通信系统应用场景为浅海，则传播损失计算公式中扩展系数可定义为 1.5。若不考虑接收端的指向性，则发射声源级将由通信距离、通信体制及海洋环境噪声决定。

本方案中采用M元扩频通信作为IBFD-UWA通信系统体制，在考虑误码率的情况下，拟定最低解调需求下的SINR为0，频带范围为8～16 kHz。海洋环境背景噪声成分复杂，一般可视为各类噪声如风浪噪声、航运噪声、湍流噪声、热噪声的综合叠加的结果，可由文献[28]中所述计算方法得到。基于

上述描述，可计算出不同距离下保证通信质量的声源级。但由于短程传播损失难以用球面波扩展来计算（考虑IBFD-UWA通信系统近端发射端到近端接收端的距离为米的量级），结合前期实验验证结果[13]，可认为近端接收端处的声压级在壳体的影响下与发射端声压级基本一致（该假设目的为保留部分自干扰抵消能力冗余）。在保证接收端期望信号 SINR的条件下，若环境噪声级提高，则需提高发射声源级，此时，若不考虑节点内部设备等因素带来的影响，发射端与远端接收端的能量差仅与传播损失有关，因此可认为海洋环境噪声级对IBFD-UWA通信系统自干扰抵消需求没有影响。

基于上述假设，绘制公里级别下，以扩频通信系统为核心的 IBFD-UWA通信系统的通信距离与SIC需求关系变化如图2所示。由图可知，若实现4 km的IBFD M元扩频UWA通信，则至少要实现75 dB的SIC，且当总的SIC能力超过70 dB时，SIC性能每提高10 dB，则该IBFD-UWA通信系统可通信距离将会增大约1倍。

2 基于RSIA的IBFD-UWA通信系统结构

为提高系统整体SIC性能，本节将基于文献[16]所述的数字辅助模拟干扰抵消（Digitally Assisted Analog Self-Interference Cancellation，DAA-SIC）技术，文献[19]所述的基于辅助链路的功放输出获取技术并结合基于 RSIA的新型系统结构设计，实现模拟域、数字域联合下的 SIC，主要分成2种方案在发射链路存在噪声干扰的情况下进行性能对比。

RSIA结构核心理念为通过2个采集链路（主采集链路、辅助采集链路）分别获取干扰信号与期望信号的混合信号以及“纯净干扰”，后者的获取方法为在通过芯片选型等方法下控制ADC有效量化位数可使期望信号无法进入指定ADC的动态量化范围之内，而主采集链路选用的ADC芯片需具备较高的有效量化位数，在此基础上再对2种方案进行分析。

方案一中，通过辅助链路实现对自干扰信号非线性失真分量的获取，并以此作为线性自适应滤波器的输入参考信号，实现DAA-SIC，并通过RSIA结构中的辅助采集链路在数字域与重构干扰信号合并（抵消）以获取残余 SI信号，以此作为数字域SIC过程中的线性自适应滤波器输入参考信号，实现进一步的残余SI的抵消。

方案二中，以本地发射信号作为线性自适应滤波器的输入参考信号，实现DAA-SIC并通过RSIA结构中的辅助采集链路在数字域与重构干扰信号合并（抵消）以获取非线性失真分量，再以此作为数字域SIC过程中的线性自适应滤波器输入，实现残余SI的抵消。2种方案差异主要在于非线性失真分量抵消过程分别在模拟域、数字域进行，同时模拟域SIC的输入参考信号不同，系统的整体方案如图2所示。

在本通信系统中，采用 M元扩频通信体制，发射信号s(t)可表示为

式中：A为发射信号幅度；ci(t)为码长为N的序列，码片持续时间为Tc的扩频码；φ为初始相位。经过功放后的输出信号ypa(t)可通过基于 Volterra级数模型[29]表示如式（3）所示：

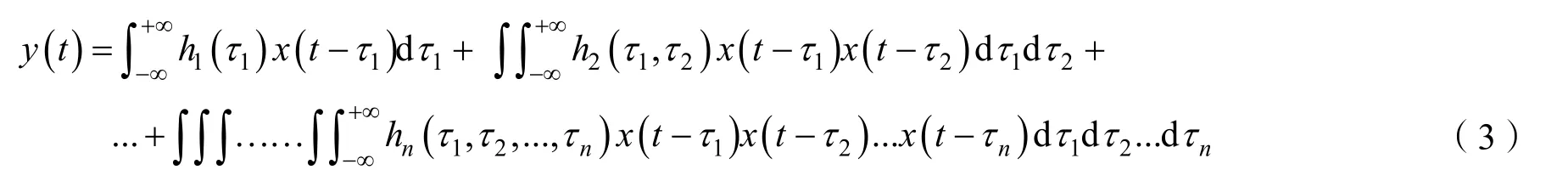
式中：s(t)为输入信号；hn(τ1,τ2, ...,τn) 为第n阶Volterra核函数表示为第n阶非线性 Volterra冲激响应，τn表示为第n阶相应的时延。通过辅助链路，经过衰减器采集到数字域时，ypa[n]可通过记忆多项式（Memory Polynomial，MP）模型[30]可进一步简化为

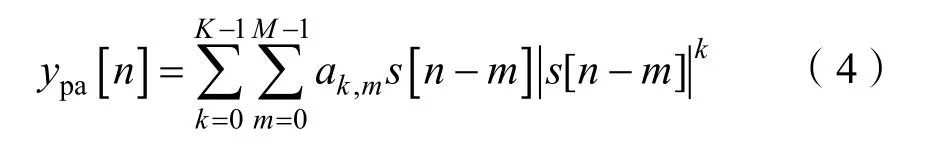
式中：K及M分别为模型的非线性阶数与记忆深度。发射信号通过换能器发出后，传播过程中经历自干扰传播信道hSI(τ,t)与期望信号混合被接收端接收，因此，图2中主采集链路接收信号r(t)可表示为

式中：⊗为卷积符号；xf（t）为远端期望信号；n（t）为噪声。根据图 1可知，若通信距离为 5 km，则此时干扰信号与期望信号的干信比（Interferenceto-Signal Ratio，ISR）约为80 dB，期望信号能量影响极其有限，因此在初步的模拟SIC过程中可不考虑期望信号对线性滤波器进行 SI信道估计精度的影响，即可认为r(t) ≈ypa(t) ⊗hSI(τ,t)。

若线性滤波器权值系数长度为Lc，则此时重构的干扰信号ysic[n]与抵消后信号easic[n]的关系为

方案核心内容在于在进行DAA-SIC的同时，通过辅助采集链路采集未经模拟域SIC的SI信号，并在其进入到数字域后，与ysic[n]进行相减得到yrsi[n]，以完成 RSIA，并以此作为线性滤波器的输入参考信号，完成数字域残余SIC。

3 理论仿真及结果分析

3.1 仿真假设

为了评估上述两通信系统方案的性能，在本节进行数值与电路仿真，为了得到真实工程应用中的实际性能，在理论仿真中分别加入了辅助链路电路噪声、功率放大器非线性失真效应、发射机噪声、复杂SI传播信道、理论ISR等方面的影响，假设及其依据如下。

1）辅助链路电路噪声以链路中的 ADC有效量化位数（Effective Numbers of Bits，ENOB）影响的形式体现，分别在辅助链路设置 52.14 dB、41.06 dB、29.98 dB信噪比（此处指参考信号与链路噪声能量之比，在本仿真中噪声形式为全频带加性高斯白噪声，分别对应文献[31]中的10，8，6位有效量化位数）；

2）通过MP模型模拟功放对发射信号的影响，模型中非线性阶数与记忆深度分别设定为5和4；

3）仿真中发射机噪声来源于功放噪声，且假设为全频带加性高斯白噪声，能量强度参考无线电发射机噪声能量强度——较输出信号能量小60 dB[30]；

4）自干扰传播信道采用文献[13]中所述实测结果，远端期望信号传播信道采用2019年12月实测千岛湖声速剖面进行仿真；

5）ISR为80 dB，对应约为5 km通信情况，由第2节计算得到。

6）线性自适应滤波器①、②设定为递归最小二乘（Recursive Least Squares，RLS）滤波器，滤波器长度分别为400、10，遗忘因子λ设定为0.999。

两方案中所述数模、模数转换器时钟绝对同步，通信系统采用M元扩频通信体制，信号调制码长为31，中心频率12 kHz，带宽8 kHz，仿真中SIC性能通过式（8）进行评价，与文献[19]思想一致。

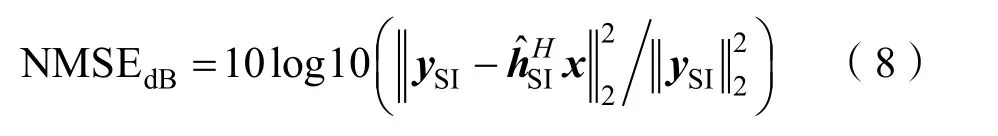
3.2 数值仿真结果分析

为便于展示各方案及参数对干扰抵消结果的影响，突出变化趋势，对干扰抵消结果进行带内滤波，并通过滑动平均进行归一化均方误差（Normalized Mean Square Error，NMSE）曲线平滑并进行降采样显示，各参数配置下SIC后的NMSE性能对比结果如图3所示，模拟域SIC后频带内能量对比如图4所示，模拟域结合数字域SIC后频带内能量对比图如图5所示。

图3 各参数配置下NMSE性能对比Fig.3 Comparison of NMSE performances under various parameter configurations

图4 模拟域SIC后频带内能量对比Fig.4 Comparison of power in frequency band after SIC in analog domain

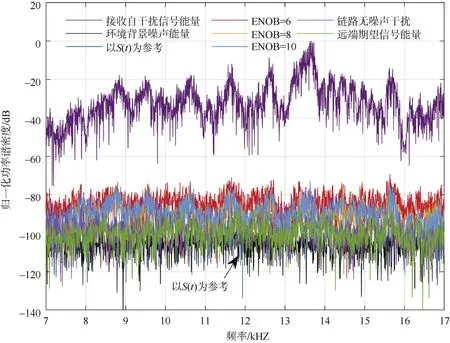
图5 数字域SIC后频带内能量对比Fig.5 Comparison of power in frequency band after SIC in digital domain

由图 3可知，辅助链路噪声干扰将影响DAA-SIC性能，当ENOB分别为6、8、10位时，模拟域SIC稳态性能分别约为38.2 dB、49.2 dB、59.8 dB，在数字域结合RSIA结构实现数字域SIC后，稳态性能可分别提升至约62.6 dB、72.4 dB、70.4 dB，性能提升量随ENOB的增加而降低，在一定程度上证明了文献[32]所述推测，即当模拟域SIC性能过强时，数字域 SIC所带来的增益效果将会下降。当辅助链路无噪声干扰时，通过DAA-SIC结构可以将SI做到较为完美的抵消（辅助链路可获取非线性失真分量），但这种理想情况因硬件条件固有噪声而无法实现，在图3中将其列出用于对比噪声干扰对SIC性能影响。当模拟域SIC过程以本地发射信号作为线性滤波器输入参考时，SIC稳态性能仅能达到约37.1 dB，这是由于该过程未将非线性失真分量考虑在内，而结合 RSIA结构实现数字域SIC后，稳态性能可提升至约78.3 dB的水平。

由图4可知，在链路噪声干扰的影响下，由于残余SI能量较大，无法通过独立的模拟域SIC实现IBFD-UWA通信，当无噪声干扰时，模拟域SIC后剩余能量与远端期望信号能量接近。图4中以本地发射信号为参考信号下，SIC后信号能量基本在通频带内均匀分布，这代表由复杂 SI传播信道造成的线性分量 SI的绝大部分已经被抵消，此时残余SI的主要成分为非线性失真分量。

由图5可知，当完成数字域SIC后，方案一中辅助链路存在噪声干扰时，各参数设置下的SIC稳态性能都得到了增强，但ISR仍在通信系统无法顺利解调的水平（＞10 dB）。但当模拟域SIC过程中，若以残余干扰作为线性滤波器①的输入参考信号，并通过RSIA结构从残余干扰中获取到非线性失真分量并作为线性滤波器②的输入参考信号，在数字域SIC阶段进行抵消，则可使系统整体的SIC性能接近辅助链路无噪声干扰下的SIC稳态水平，可进一步降低ISR，进而支撑IBFD M元扩频UWA通信系统的顺利解调。

3.3 电路仿真结果分析

为进一步证明模拟域 SIC过程选用不同参考信号下 SIC效果性能差异，通过 MATLAB的Simulink模块对各方案及参数设定进行实测硬件参数下的电路仿真与性能分析。

具体参数获取过程如下：用T类功率放大器进行SI信号发射，通过级联两低噪衰减器（Behringer DI-100）直接采集获得功放输出信号，并通过计算求得发射机噪声能量水平（计算结果约为61 dB），其次通过对功放输出衰减回路信号对功放进行建模以获得MP模型参数。

发射信号参数设置与仿真过程保持一致。各采集链路噪声以加性高斯白噪声形式出现，其余参数设定与仿真过程保持一致。各方案及不同参数下SIC后频带能量对比如图6所示，理论及与电路仿真SIC稳态性能对比如图7所示。

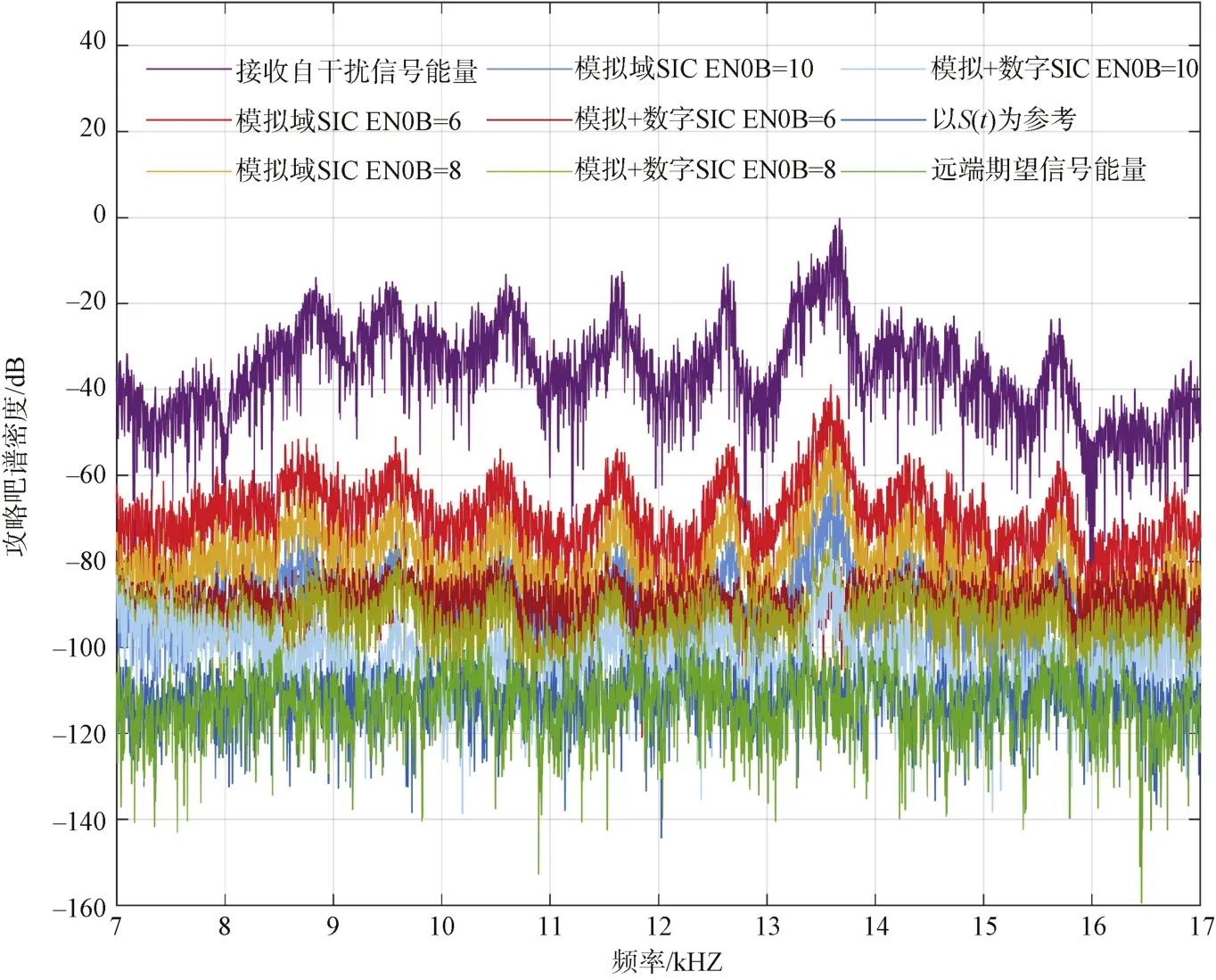
图6 模拟及模拟、数字域联合SIC后频带内能量对比Fig.6 Comparison of power in frequency band after analog and analog & digital domain combined SIC

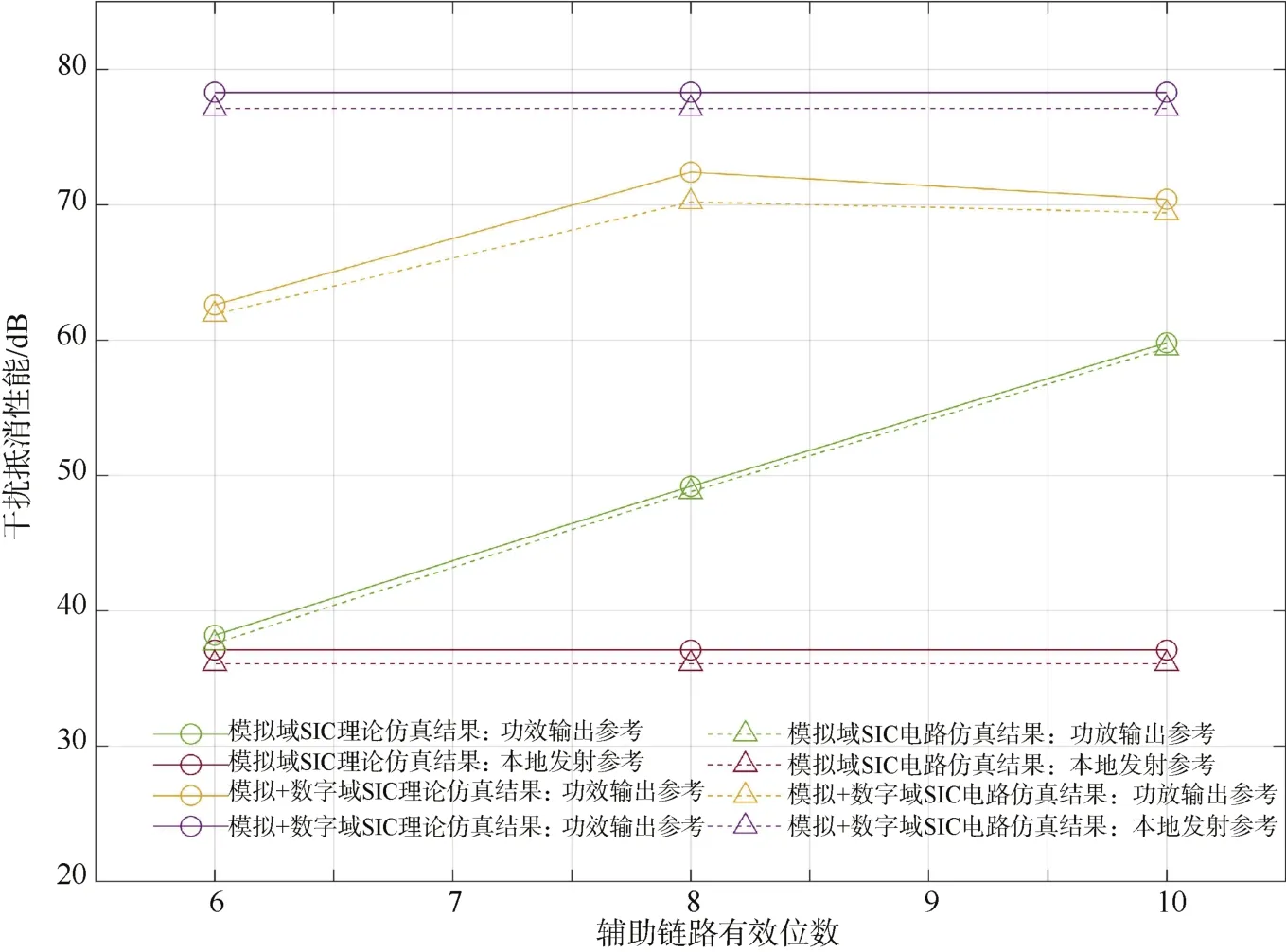
图7 模拟及模拟、数字域联合方案的理论与电路仿真SIC稳态性能对比Fig.7 Comparison of SIC steady-state performances between analog，analog & digital domain joint scheme in theory and circuit simulation

由图6可知，电路仿真结果中模拟及模拟、数字域联合SIC后频带内能量对比结果与图4及图5基本保持一致，具体细节差异可见图7。

由图7可知，实测硬件参数下的性能仿真结果中的 SIC稳态性能变化规律与理论仿真结果基本一致，但性能均有所下降，推测其原因为理论仿真与电路仿真中功放模型系数不一致导致。模拟、数字域联合SIC后IBFD M元扩频UWA通信系统误码率情况如表1所示（Monte-Carlo仿真50次）。

表1 模拟、数字域联合SIC后IBFD M元扩频UWA通信系统误码率Table 1 BER of IBFD M-ary spread spectrum UWA communication system after analog and digital domain combined SIC

为体现残余干扰对通信系统影响，解调过程无均衡及解码过程。由表1可知，当通过辅助链路将功放输出信号引入数字域作为线性滤波器输入参考信号，再在数字域进行残余SIC时，由于存在模拟域及数字域SIC性能的平衡问题，无法使干扰强度降低至系统可顺利解调的程度。而本文所述基于RSIA的IBFD-UWA通信系统结构并利用本地发射信号完成初步的模拟域SIC，可使通信系统实现误码率小于10-3的通信效果。

4 结束语

本文提出了一种基于残余干扰获取的带内全双工扩频水声通信方案，理论与电路仿真结果表明，该方案可在有效克服功率放大器非线性影响的同时，通过辅助采集链路获取“纯净”干扰信号，并引入至数字域内获得残余 SI的近似样本，并通过进一步的数字域 SIC完成残余 SI的抵消，使SINR提高至M元扩频通信系统可解调水平。但需指出，该结构会造成远端期望信号存在一定损失，因此目前该结构仅能采用抗干扰能力较强的通信体制进行实现，同时除本文中讨论的参数影响外，方案还将受限于衰减器、减法器（合并器）、低噪放大器的实际性能，未来将对此类器件影响及新型“模拟-数字联合结构”进行更深入地研究。