基于能量分析的唐代殿堂型木构架抗震机理研究

王 娟，许刃文，杨庆山，张熙铭，杨 娜

(1. 北京交通大学土木建筑工程学院，北京 100044；2. 结构风工程与城市风环境北京市重点实验室，北京 100044；3. 重庆大学土木工程学院，重庆 400044)

古建筑木结构是华夏文明的文化载体，具有极其重要的历史文化与科学研究价值。以木构架为基础的多层减隔震体系是其抵抗地震作用的关键[1]，包括木柱与石基之间的摩擦滑移[2-3]、半刚性榫卯节点的摩擦挤压[4-6]、铺作层的耗能减震[7-8]。汶川地震震害调查[9]显示，仅有少数年久失修的木结构古建筑发生整体垮塌破坏，表明古建筑木构架拥有良好的抗震性能。

我国现存最早的古建木构类型—唐代殿堂型木结构，具有斗拱与梁架一体化的铺作层和横向联系较弱的柱架层，是其区别于后世古建筑木结构的主要特征。五台山佛光寺东大殿即为此类型，在千年之久的历史中，经历数次地震作用仍屹立不倒。然而因建造年代久远，唐代殿堂型木结构不可避免地存在残损[10]，面临结构安全风险。因此，为揭示其抗震机理，对其进行科学保护与修缮，针对唐代殿堂型木构架开展了摇摆抗侧机理研究[11-13]。结果表明：木构架在水平低周反复荷载作用下滞回曲线捏缩效应明显(图1)，滞回耗能能力较弱，但变形能力强，在水平荷载下会发生摇摆抬升(图2)。由于古建木构“大屋盖”的特点，竖向抬升过程中将产生较大重力势能变化，进而影响木构架中的能量分配。

从能量角度探究结构抗震机理，即将地震作用视为能量的输入和耗散过程，弥补了单一承载力或位移指标在进行抗震设计时无法考虑累积损伤效应的影响[14]。基于能量角度的抗震设计思想自HOUSNER[15]提出以来，并经学者们不断完善[16-19]，近年来已广泛应用于不同类型结构的抗震设计中[19-21]。在古建筑木结构领域，尽管已有学者探究了宋代木构架中的能量问题[22-23]，但都是基于拟静力试验与模拟展开的分析与讨论，尚存局限。因此，有必要基于动力时程分析，从能量分析角度进一步揭示唐代殿堂型木结构的抗震机理。

木构架中存在成百上千个榫卯节点，构件间产生的累积耗能不可忽视。为精细化模拟实际结构，以可表征铺作层协同工作特性的唐代殿堂型单间四柱木构架为研究对象，建立了全实体精细化有限元模型并进行了动力时程分析，通过木构架中的能量组成及变化规律分析揭示其抗震机理，同时研究了地震作用参数及斗拱-梁架一体化铺作层构造、柱头馒头榫弱连接节点形式、竖向荷载大小等结构参数对木构架中能量的影响。

1 摇摆木构架的能量平衡关系

当地震作用于古建筑木结构时，是以能量的形式传递给木构架，在构架摇摆抬升过程中，能量一部分储存于木构架之中，另一部分通过耗能机制耗散掉。由结构动力学可知，考虑阻尼条件下，水平地震作用时木构架在任意t时刻的运动方程如下：

式中：EK(t) 为 结构t时刻对应的动能；ED(t)为结构t时刻对应的粘滞阻尼耗能；ER(t)为结构t时刻对应的非线性恢复力做功；EI(t)为结构t时刻对应的总输入能量，即结构在地震作用下吸收的总能量。非线性恢复力做功包括弹性应变能、塑性耗散能、摩擦耗能及重力势能。

在木构架往复摇摆过程中，动能与重力势能及弹性应变能不断转化，木构架不断通过阻尼、摩擦及塑性应变耗能，其示意图如图3 所示。这与现代钢结构及混凝土结构有较大不同：一方面木构架构件中存在较多的榫卯节点，在大震作用下榫卯间的接触面会产生较大的摩擦耗能；另一方面，以混凝土结构为例，其在地震作用下动能主要转化为弹性应变能，原因是其在地震作用下其抬升位移较小，重力势能变化不明显。

2 唐代殿堂型木构架动力时程分析

2.1 木构架精细化有限元模型

以某一唐代殿堂型木构架为研究对象，在现场调研及参考相关文献的基础上，建立了可表征铺作层空间协同工作特性的单间四柱木构架模型(图4)。该模型由草乳栿、素枋、明乳栿、横向华栱、纵向柱头枋、散斗、暗销、栌斗、木柱等238 个构件组成。木构架主视图及左视图如图5、图6 所示。模型外露部分尺寸及构造参考文献[10]中现场勘查数据，隐藏尺寸及构造参考文献[24 - 25]，具体尺寸列于表1。

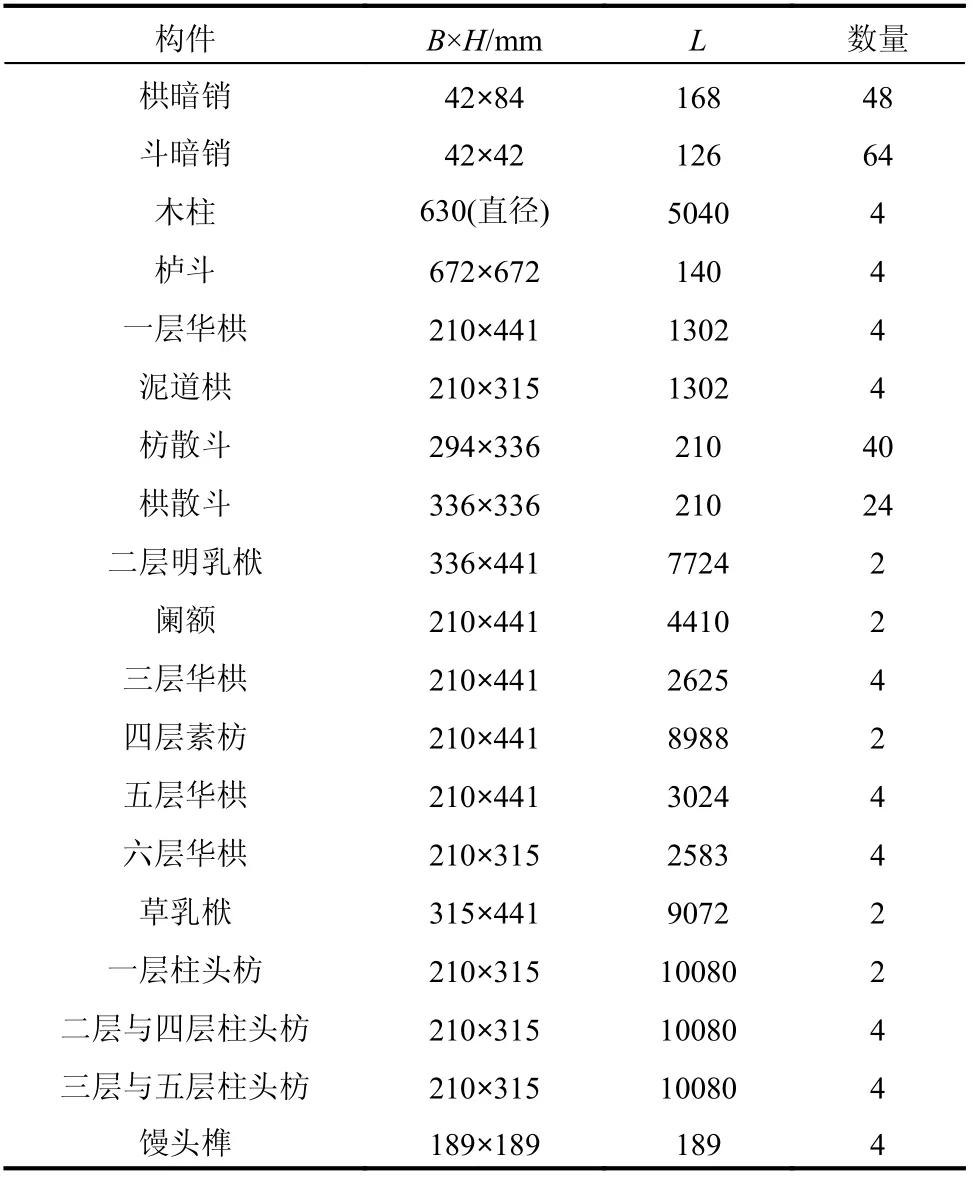
表1 木构架组成构件尺寸Table 1 Dimensions of components of the timber frame model

木构架材料为樟子松[26]，采用Hill 屈服准则来描述其进入塑性阶段的力学行为[27]。木材材料参数列于表2。樟子松密度取 4 .34×10-10t/mm3，础石弹性模量取 3×104MPa ， 密度取 2.50×10-9t/mm3，泊松比取0.2。

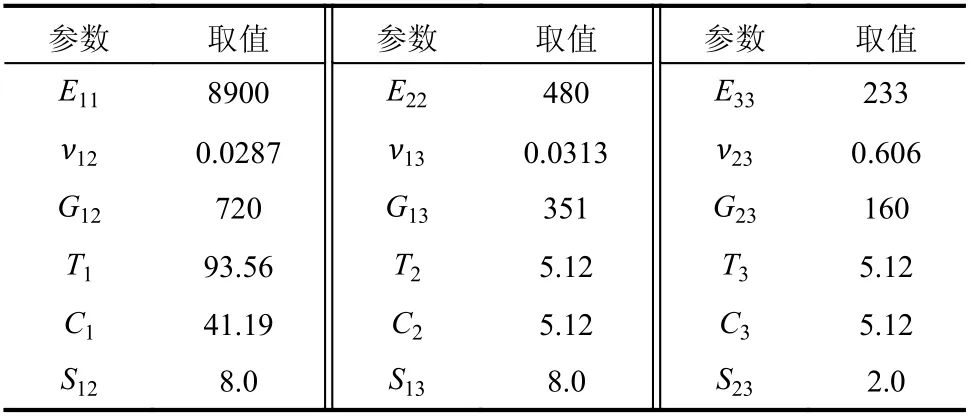
表2 木材材料参数Table 2 Property parameters of timber

基于ABAQUS 有限元软件建立木构架精细化有限元模型，如图7 所示。模型采用C3D8R 实体单元，总数约10 万。

础石底面固定，木柱底端平摆浮搁于础石上。构件通过榫卯及暗榫相互连接，考虑构件间的接触挤压及摩擦滑移作用，接触类型采用法向硬接触和切向库仑-摩擦接触。木材接触面之间摩擦系数设置为0.45，木材与础石、质量块之间摩擦系数取0.6[26]。

参考文献[28]中关于木构架试验与有限元对比可知，阻尼比取3%时获得的动力响应较为合理，因而阻尼比取3%。结构阻尼采用瑞利(Rayleigh)阻尼，其计算公式为：

式中：ωi为第i阶阵型的自振频率； ζi为第i阶阵型的阻尼比。带入频谱数据得： α=0 ， β=0.028。

2.2 建模方法有效性验证

首先使用2.1 节中的建模方法建立单跨两柱木构架有限元模型，并将其与文献[13]中拟静力试验进行验证(图8)，结果表明：数值模拟的骨架曲线及整体变形与拟静力试验结果吻合较好，由此表明木构架的建模方法具有一定有效性。在此基础上采用同样的建模方法建立了本文的单间四柱木构架模型。

2.3 地震记录选取

原型木结构所在的场地类型，其抗震设计分组为第二组，场地类别为Ⅱ类场地，特征周期Tg取为0.4 s。采用文献[29]中建议的最佳选波原则，从美国太平洋地震研究中心中选择了4 条地震记录作为弹塑性时程分析的地震动输入。各条输入地震动反应谱、平均谱以及规范谱如图9 所示。

针对唐代殿堂型木构架进行弹塑性非线性有限元动力分析时，考虑到地震动持续时间T应包括地震记录最强的部分，且T≥T1，其中T1为基准模型结构的基本周期0.963 s，因此动力时程分析中地震持时取为25 s。

2.4 能量影响参数分析工况

唐代殿堂型木构架中复杂铺作层是其区别于其它类型木构架的典型构造特征；柱头馒头榫为木构架铺作层与柱架层的连接构造，抗侧刚度在此处发生突变；此外木构架“大屋盖”的特点使其基于竖向抬升产生的重力势能影响不可忽视。上述均为唐代殿堂型木结构的典型结构特征，有必要探究这些参数对木构架中能量的影响。此外，加速度幅值及不同卓越周期地震波也可能对木构架中的能量分布规律产生影响。因此，共设置了16 种动力时程分析的工况(表3)，考虑地震作用参数及斗拱-梁架一体化铺作层构造、柱头馒头榫弱连接节点形式、竖向荷载大小等结构参数对唐代殿堂型木构架能量的影响。不同工况分析模型示意图见图10。

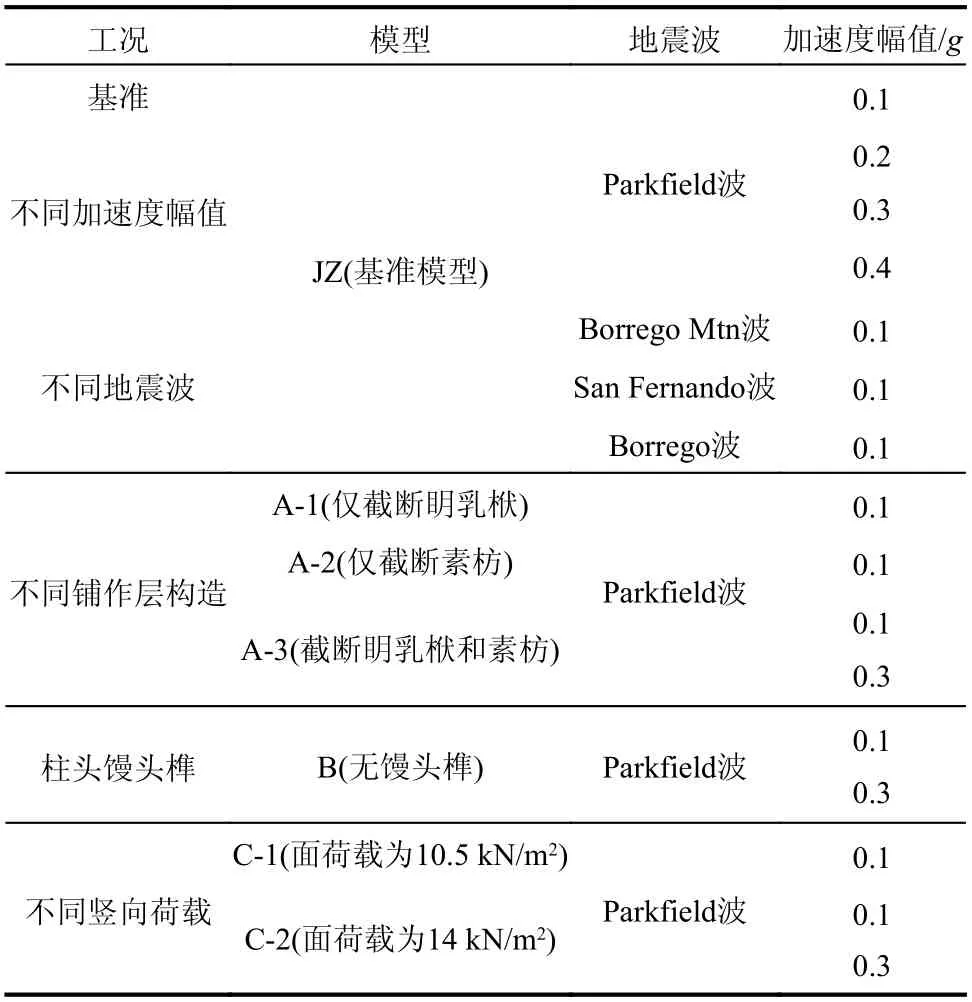
表3 分析工况Table 3 Analysis conditions

3 唐代殿堂型木构架能量分析

3.1 基准工况分析结果

针对唐代殿堂型木构架基准模型进行弹塑性时程分析。由文献[30]可知，ABAQUS 有限元软件基于有限元原理计算得到能量指标可满足结构地震能量分析需求，则从ABAQUS 有限元软件后处理中获取动能、阻尼耗能及非线性恢复力做功中的弹性应变能、塑性耗散能、摩擦耗能，重力势能可通过提取木构架的竖向位移，然后，由公式Eh=mgh计算获得。

当加速度幅值为0.1g时，基准模型中动能、阻尼耗能和恢复力做功及总输入能的能量分布见图11(a)。在水平地震作用下，木构架产生摇摆抬升运动，阻尼耗能随地震输入而不断增加，阻尼耗能在总输入能中占比约为60%，为总输入能的主要部分，结构动能伴随结构速度的变化上下波动。恢复力做功随地震输入起伏波动，且随动能增加而减少。图11(b)为恢复力做功中各项能量的分布图，在恢复力做功中弹性应变能占主要部分。木构架竖向抬升位移最大值仅为1.14 mm，即使屋盖质量较大，其重力势能仍然较小。不过在部分时刻模型的重力势能占恢复力做功的比例仍可达到30%，由此可见即使在摇摆抬升量较小的情况下重力势能对木构架的影响也不可忽视。在该加速度幅值的地震作用下，模型通过阻尼与摩擦力耗能，其中阻尼耗能约占90%以上，是木构架中主要耗能方式，由于木构架中构件还未进入塑性，因此，未产生塑性耗能。如图11(c)所示，重力势能与弹性应变能变化趋势相同，均随动能减小而增大，输入结构的动能部分转化为重力势能与弹性应变能，但转化量较小，此时木构架储存的重力势能较小。

3.2 加速度幅值的影响

当加速度幅值为0.3g时，模型JZ 中动能、阻尼耗能和恢复力做功及总输入能的能量分布见图12(a)。当地震作用较大时，阻尼耗能在总输入能中占比显著下降，而恢复力做功占比显著增加。图12(b)为恢复力做功中各项能量的分布图。其中重力势能在恢复力做功中占比显著提高，成为恢复力做功的主要部分。可见当加速度幅值增大时，木构架产生的竖向位移也逐渐增大，重力势能不断增加。木构架摇摆抬升时，竖向位移增加，速度减小，即木构架重力势能增加，动能减小；当木构架抬升至最高点后，开始反向复位，竖向位移减小，速度增加，即木构架重力势能减小，动能增大。木构架在这样往复摇摆抬升复位过程中，重力势能、弹性应变能与动能之间不停转化。图12(c)为动能与重力势能及弹性应变能之间的相互转化关系。当加速度较大时，由于木构架摇摆抬升位移较大，木构架可存储较大重力势能，于是输入木构架的动能大部分都转化为木构架的重力势能，从而使木构架中产生的塑性应变能较小，极大地减小了动能可能对结构构件造成的损坏。木构架通过不断反复摇摆抬升为其消耗地震能量争取了时间。由此可见，摇摆抬升在木构架抵抗地震过程中发挥了十分重要的作用。

图13(a)～图13(d)分别为不同加速度幅值下的总输入能、阻尼耗能、恢复力做功及动能的能量分布图，在水平地震作用下，不同加速度幅值下木构架的总输入能及阻尼耗能均不断增大，且输入的加速度幅值越大，木构架的总输入能及阻尼耗能越大。恢复力做功及动能随地震动的输入变化而起伏波动，加速度幅值越大波动幅值越大。

图14(a)～图14(d)分别为不同地震加速度幅值作用下恢复力做功中的弹性应变能、摩擦耗能、塑性耗散能及重力势能的能量分布图，塑性耗散能及摩擦耗能随地震动的输入不断增加，且加速度幅值越大塑性耗散能及摩擦耗能越大。弹性应变能与重力势能均随地震动的输入变化而不断起伏波动，加速度幅值越大波动幅值越大。

3.3 不同地震波的影响

图15(a)～图15(d)分别为不同地震波作用下的总输入能、阻尼耗能、恢复力做功及动能的能量分布图。向木构架施加相同加速度不同卓越周期的地震波时，木构架得到的总输入、阻尼耗能、恢复力做功及动能有较大差异。在Borrego Mtn 波与Borrego 波作用下木构架的总输入能及阻尼耗能值明显大于Parkfield 波及San Fernando 波，在Borrego Mtn 波作用下木构架的恢复力做功及动能值明显大于其它三条地震波。四条地震波的卓越周 期 大 小 为：Borrego Mtn 波＞San Fernando 波＞Borrego 波＞Parkfield 波，可见虽然不同卓越周期地震波的能量关系明显不同，但能量变化与地震波卓越周期的关系并不明显。

4 结构构造影响参数分析

4.1 不同铺作层构造的影响

当加速度幅值为0.1g时，不同铺作层构造下木构架的总输入能、阻尼耗能、恢复力做功及动能的能量分布对比分别如图16(a)～图16(d)所示，不同铺作层构造模型的总输入能曲线变化趋势基本一致。四种不同铺作层构造模型的阻尼耗能均随地震输入逐渐增加，具体大小关系是JZ＞A-2＞A-1＞A-3，JZ 的阻尼耗能相比A-2、A-1、A-3 分别最大高出5%、10%及15%，产生的原因是截断铺作层内的眀乳栿、素枋，使眀乳栿、素枋这些构件内部颗粒摩擦产生了变化，于是木构架的阻尼耗能也产生了变化。不同铺作层构造模型的恢复力做功及动能交替起伏波动，四种不同铺作层构造模型的动能变化及恢复力做功曲线相似，但在具体数值上，模型JZ、A-1、A-2 相差不大，均与A-3 出现峰值的时间存在一定差异。图17(a)～图17(c)分别为不同铺作层构造下水平向的柱顶、铺作层、屋盖的速度对比图，这里取木构架的四根木柱柱顶的水平平均速度作为木构架的柱顶速度，木构架与铺作层质心位置相近的素枋中心的平均速度作为铺作层速度，质量块的平均速度作为木构架屋顶的速度。模型JZ、A-1、A-2 的水平速度相差不大，均与A-3 在部分时间段存在一定差异，该规律与动能变化规律一致。

当加速度幅值为0.1g时，四种不同铺作层构造模型下的恢复力做功中各项能量分布如图18(a)～图18(c)所示，四种不同铺作层构造模型中的构件均未进入塑性，都没有产生塑性耗能。四种模型中弹性应变能的变化趋势与恢复力做功变化趋势相似，弹性应变能均是恢复力做功中的主要部分，摩擦力随地震输入不断增大，由于此时输入地震波幅值较小，木构架模型摇摆幅度较小，木构架中构件的相互挤压摩擦作用也较小，因而此时其在恢复力的占比较小。与恢复力做功相似，模型A-3 与模型JZ、A-1、A-2 相比，重力势能曲线变化存在略微滞后，这主要是因为地震作用力由柱底向上传递至铺作层时， A-3 模型中铺作层联系相比模型JZ、A-1、A-2 较弱，铺作层左右两侧受到下部传递而来的地震作用力后运动的一致性受到影响，导致其铺作层及模拟屋盖作用的质量块相比其它模型摇摆抬升过程略微滞后，而铺作层及模拟屋盖作用的质量块是木构架质量的主要组成部分，因而其重力势能曲线变化也略微滞后。

当加速度幅值为0.3g时，模型JZ 与模型A-3的总输入能、阻尼耗能、恢复力做功及动能的能量分布如图19(a)～图19(d)所示，总输入能、阻尼耗能、恢复力做功及动能的变化趋势与加速度幅值为0.1g时的变化趋势相似，均随地震作用的输入，总输入能与阻尼耗能不断增加，动能及恢复力做功交替起伏波动。与加速度幅值为0.1g时不同的是，模型A-3 的总输入能及阻尼耗能在部分时刻相比模型JZ 高出23%以内及12%以内。可见不同铺作层构造对总输入能、阻尼耗能、恢复力做功及动能的变化趋势影响较小，但由于铺作层构造的改变使木构架铺作层的整体性发生了变化，尤其是同时截断乳栿和素枋时(模型A-3)，木构架在地震荷载作用下速度发生了变化进而导致动能变化，同时铺作层构造的改变也改变了结构构件的整体性进而导致阻尼耗能的变化，最终导致总输入能的变化，但总体上变化较小。

4.2 柱头馒头榫的影响

当加速度幅值为0.1g时，模型B 中动能、阻尼耗能和恢复力做功及总输入能的能量分布如图20(a)所示，动能、阻尼耗能和恢复力做功及总输入能的变化趋势和基准模型JZ 相似，其中总输入能及阻尼耗能与模型JZ 在数值上也相差较小。图20(b)为模型B 中恢复力做功中各项能量的分布图，恢复力做功中各项能量的变化趋势和基准模型JZ 也基本相似。当加速度幅值为0.3g时，模型JZ 与模型B 的总输入能、阻尼耗能、恢复力做功及动能的能量分布对比如图21(a)～图21(d)所示，模型B 在动能、阻尼耗能和恢复力做功及总输入能的变化趋势与基准模型JZ 相似，表明馒头榫对木构架中能量分配的影响较小。

4.3 竖向荷载的影响

当加速度幅值为0.1g时，不同竖向荷载作用下木构架的总输入能、阻尼耗能、恢复力做功及动能的能量分布如图22(a)～图22(d)所示，在水平地震作用下，不同竖向荷载的木构架的的总输入能及阻尼耗能均在不断增大，且竖向荷载越大，木构架的总输入能及阻尼耗能越大，模型C-1(面荷载为10.5 kN/m2)和模型C-2(面荷载为14 kN/m2)的总输入能平均约为模型JZ(面荷载为7 kN/m2)的1.73 倍和2.31 倍，模型C-1 和模型C-2 的阻尼耗能平均约为模型JZ 的1.5 倍和2 倍，与竖向荷载之间的差距一致。在恢复力做功中，模型C-1 和模型C-2 的恢复力做功均显著大于模型JZ，同时模型C-1 和模型C-2 的动能也均显著大于模型JZ，尽管模型C-2 的竖向荷载是模型C-1 的1.33 倍，但模型C-2 的动能在部分时段内小于模型C-1。

当加速度幅值为0.1g时不同竖向荷载作用下木构架恢复力做功中的弹性应变能、摩擦耗能、塑性耗散能及重力势能的能量分布对比分别如图23(a)～图23(d)所示，模型C-1 和模型C-2 的弹性应变能显著大于模型JZ，当竖向荷载越大时，木构架中构件相互挤压作用越大，构件的弹性形变量也越大，导致弹性应变能越大。三种不同竖向荷载作用下木构架的摩擦耗能均随地震波的输入而不断增加，且竖向荷载越大阻尼耗能越大，主要原因是竖向荷载越大，木构架中构件相互间摩擦挤压作用越大，产生的摩擦耗能也越大。竖向荷载越大，木构架塑性耗散能也越大，原因是竖向荷载越大，构件间挤压变形越大，产生的塑性变形也越大，因而塑性耗散能也越大。竖向荷载越大，木构架重力势能波动越大，且当竖向荷载越大时，铺作层向柱顶顶面转动的幅度越小甚至出现下降，于是模型C-1 和模型C-2 的重力势能出现负值。

当加速度幅值为0.3g时，不同竖向荷载作用下木构架的总输入能、阻尼耗能、恢复力做功及动能的分布对比如图24(a)～图24(d)所示，不同竖向荷载下四种能量的变化趋势与0.1g时相似，但模型C-2 的总输入能及阻尼耗能约为模型JZ 的1.47 倍和1.34 倍，竖向荷载对总输入能、阻尼耗能的增加幅值相对0.1g时有所减弱。

5 结论

从能量角度揭示了唐代殿堂型木构架抗震机理，并探究了地震作用参数及斗拱-梁架一体化铺作层构造、柱头馒头榫弱连接节点形式、竖向荷载大小等结构参数对唐代殿堂型木构架中能量分配、分布的影响，得到以下结论：

(1) 木构架在地震作用下产生往复摇摆，在此过程中动能与重力势能及弹性应变能不断转化，期间不断产生阻尼耗能、摩擦耗能及塑性应变能。由于木构架中组成构件众多，且构件之间直接接触连接，大震作用时木构架会产生较大摩擦耗能。

(2) 在小震作用下，木构架摇摆幅度较小，重力势能变化较小，此时重力势能对木构架抵抗地震作用的影响并不明显。大震作用时，木构架摇摆抬升位移较大，输入的动能大部分转化为重力势能存储于构架之中，使得塑性应变能不至于过大，进而减小了结构构件可能的损伤。木构架的反复摇摆抬升也为消耗地震能量争取了时间。

(3) 不同卓越周期地震波及加速度幅值均对木构架的能量分配影响较大。加速度幅值越大，构架的总输入能及阻尼耗能也越大；不同卓越周期地震波对木构架中能量分配的影响无明显规律。

(4) 不同结构参数对木构架的能量分配的影响不同，馒头榫对木构架中能量分配影响较小；铺作层构造在不同地震加速度幅值下对木构架中能量分配的影响不同，当加速度较小时，铺作层联系越强，总输入能及阻尼耗能越大，当加速度较大时，铺作层联系越弱，总输入能及阻尼耗能越大；竖向荷载越大，木构架中总输入能及阻尼耗能越大。