基于超声波测距的农机行间自行走控制系统

蒿晟昆，霍静琦，张宇，李志伟

（山西农业大学农业工程学院，山西晋中 030801）

农机田间自主行走作为精准农业的关键性技术，其自动化技术可极大减轻作业人员的劳动强度，适应现代化精细农业生产的发展趋势[1]。

国内外关于农机平台路径规划均有研究，并在农机旋耕播种、农机田间施肥、植保喷药、作物收获等方面应用广泛[2]。日本的yoshisda 等人采取GPS 与FOG 相融合技术，以PH-69 插秧机为样机研究出PID算法控制农机自动驾驶[3]。周俊等对农业机器人通过机器视觉进行路径跟踪研究，设计出基于轮式农业机器人的机器视觉导航控制系统[4]。

农机导航定位的研究，基于多种方法，诸如GPS导航、双激光雷达定位、机器视觉寻迹、多传感器融合位置检测等。但是目前可应用的农机尺寸往往偏大，此类大型农机通常搭载GPS 全球定位系统，仅适合大型农场中的作业。但是田间作业往往还只能依靠人力徒步。现阶段对于狭小空间自主行走的研究主要集中在智能巡检机器人及电动智能车，对于在复杂多变的行间行驶的农机研究较少。现将农机与实际农艺相结合，针对农机目前在农业生产中所存在的缺陷，设计小型农机行间自行走控制系统具有很强的实际应用价值。

1 履带式农机运动学模型

行间自行走的控制策略和农机位置调整需要基于履带式农机的运动学模型[5]。如图1 所示为履带式农机运动学模型，分别建立全局地面坐标系XOY和农机车体坐标系xoy，农机车体坐标系位于农机车体中心处。y轴方向为农机前进方向。农机行进中转向时，农机以平面内一点作为其转动瞬心，记为点Q。农机中心点o处到点Q的连线距离即为转向半径R，农机绕点Q转动的速度即为转向角速度ω。

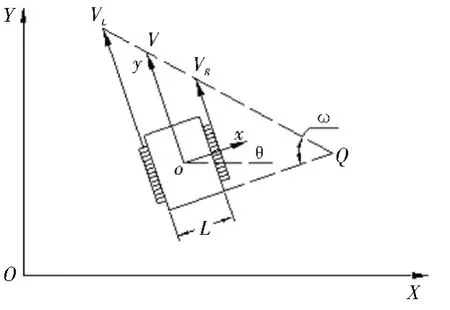
图1 履带式农机运动学模型

对履带式农机的运动学模型作如下假设：①农机时刻处在平面上运动且阻力系数固定；②两侧履带在均匀低速转向时无滑移现象出现；③两侧履带完全相同且均不影响行驶轨迹；④农机的中心点o视为实际农机质心；⑤履带式农机转向时忽略离心力和转向角速度ω的变化影响[6]。当农机以Q为转动瞬心，R为转向半径时，其左右两侧驱动轮速度、两侧履带速度和农机运行速度、转向角速度、转向半径的关系表示为式（1）-（5）。

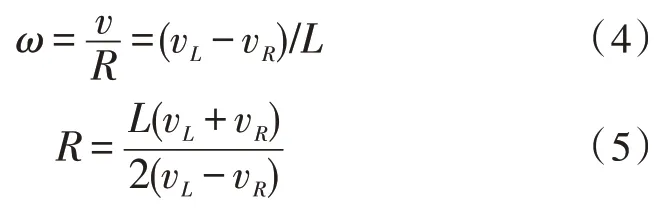
其中，ωR、ωL分别为左右两侧驱动轮的角速度，r为驱动轮半径，vR、vL分别为左右两侧履带的行驶速度，ω为农机绕点Q的转向角速度，v为履带式农机车体中心o点的线速度，L为农机车体宽度，R为农机转向半径。分析农机的不同行驶状态，当vR与vL相等，即农机直线行驶时，转向半径视为无穷大；当vR与vL大小相等方向相反时，即农机处于原地差速转向状态，转向半径为零，农机转动瞬心点Q与农机中心点o重合；当vR与vL不相等时，农机绕转动瞬心点Q以任意R作为转向半径进行转向[7]。

农机转向角速度为ω，则在Δt时间内农机运动的弧长记为E，通过弧长角度公式将农机运动的弧长转化为农机在Δt时间内转过的角度n，其与左右两侧履带行驶速度的关系可表示为式（6）-（7）：

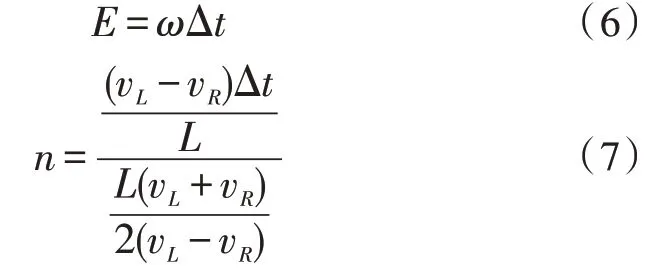
目前履带类车辆常有三种差速转向方式[8]，该文选择独立式转向方式，该转向方式对功率的需求小于中心差速式转向和外侧提速式转向。其原理是农机转向过程中，靠近转动瞬心点Q侧履带速度降低，远离转动瞬心点Q侧履带速度保持不变。

2 车身位置检测策略

目前广泛采用非接触式距离传感器有激光测距、红外测距、超声波测距；其中红外测距传感器容易受到光强影响，且范围较小，在复杂的田间环境易受干扰；激光测距精度高但是结构复杂，成本较高，适合于高精准度运行的智能巡检机器人；超声波测距方向性好，穿透力强，超声波传感器防水防污性能强，在复杂的作业环境下仍能保持较优水准[9-11]。

农机在田间作业时，传感器传输的信号常受安装位置、农机自身噪音或者环境因素变化的影响，超声波传感器输出距离信号存在较大误差，需要对超声波测得的距离信号进行预补偿处理，以保证超声波传感器输出的距离信号更加贴近实际距离。基于相对误差最小二乘法对超声波距离信号进行处理。

根据最小二乘拟合的数学定理[12]，将超声波测量值与实际值作差，选择相对误差进行拟合计算，对距离测量值与实际值的线性关系表示如下：

测量的相对误差通过最小二乘法公式表达如下，其中n为测量距离值的采样次数，在测量值中任取两组对应数据建立方程组求取M、N值：

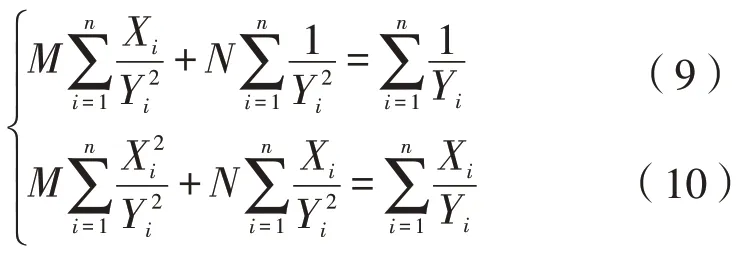
由于超声波传感器的回声测距原理，即超声波存在测量死区，通过实验测得超声波传感器测量死区为0至26 cm，所以超声波测距实验选定在27 cm 至50 cm 之间采样。实验测距结果如表1 所示。

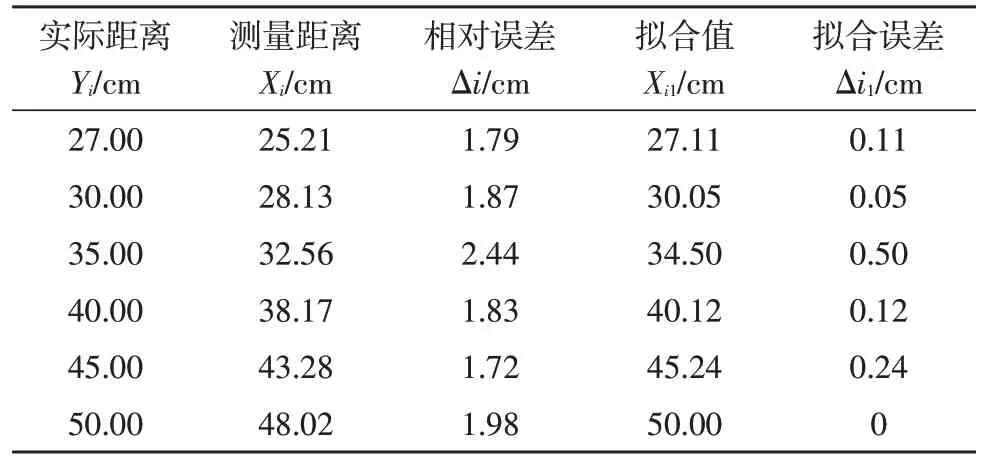
表1 超声波测距采样值

将表中距离测量值与实际值代入拟合公式（9）、（10）中，解得M=1.077 0、N=-4.070 8，则实际距离值和超声波测量距离值的关系按式（11）拟合：

通过表1 对比最小二乘拟合前的相对误差值与最小二乘拟合后的相对误差值，处理后的超声波测量值准确度和稳定度有较为明显的改善。

利用传感器分别对车右前侧、左前侧、右后侧、左后侧的距离进行检测，且超声波的安装位置到车体最外侧的距离需大于超声波自身测量死区，以保证超声波工作在正常测距范围内。图2 所示为通过超声波测量距离值对农机行驶航向角偏差进行分析计算示意图。

图2 中，a为车身左前侧测量的距离值，b为左后侧测量的距离值，c为农机长度，θ为农机车体坐标系y轴与全局地面坐标系Y轴之间的夹角，即农机相对于行间直线行驶时的航向角偏差值。根据梯形几何关系得到两者关系公式，如式（12）所示：

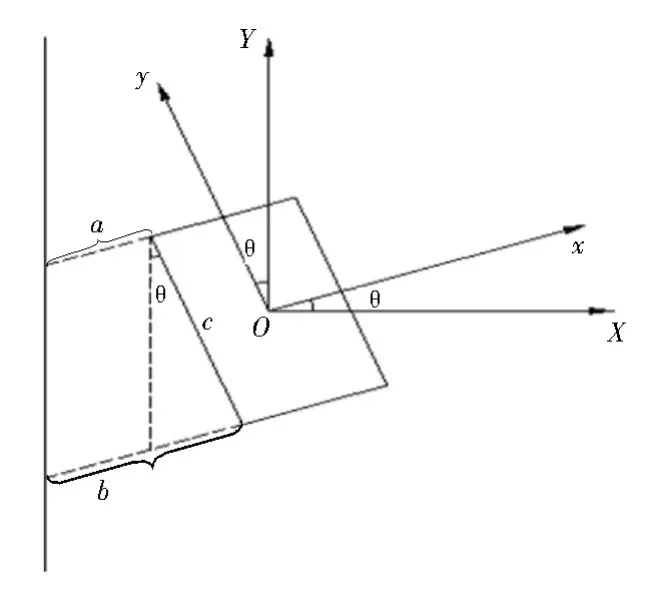
图2 航向角偏差计算示意图

如图3 所示，车体中心位置垂直于两侧农作物种植行的直线距离作为农机距两侧农作物的距离d1，当农机在行间中心线正常行驶时，存在几何关系：a=b=d1，当农机存在航向角偏差和位置偏差时，根据几何关系有：

图3 位置偏差计算示意图

式（16）利用车身前后四个超声波传感器的测量值计算农机作业时，将车身航向角偏差θ和车身相较于行间中心线的位置偏差d作为下文模糊控制算法的输入量。

3 自行走模糊控制策略

模糊控制法利用模糊数学的基本思想和理论，在分析复杂多变环境下的系统时，变量往往难以用传统控制理论描述，因此引入模糊控制理论来简化系统的动态分析与控制，其能够效仿该领域专家的经验和策略，智能决策能力远超传统控制理论。一个模糊控制器通常包含模糊化、模糊决策、解模糊化[13-14]。

航向角偏差θ、位置偏差d与行间行驶中心线的位置关系大致有图4 所示的几种情况。规定当车体位置偏差在行间中心线左侧时，位置偏差d为负值；当车体位置偏差在行间中心线右侧时，位置偏差d为正值。车头行驶方向指向左前方时，航向角偏差θ为负值；车头行驶方向指向右前方时，航向角偏差θ为正值。图4（a）表示位置偏差为负，航向角偏差为0；图4（e）表示位置偏差为0，航向角偏差为负；图4（i）表示位置偏差为正，航向角偏差为正。

图4 航向角偏差、位置偏差示意图

模糊控制规则的建立基于人工驾驶农机的操纵经验，其建立规则应该符合实际操纵方式：当车体位置偏差d、航向角偏差θ与行间中心线偏差较大时，应尽快调整方向，防止农机驶入两侧作物中；当车体位置偏差d、航向角偏差θ与行间中心线偏差较小时，对于消除偏差和农机行驶稳定性要兼顾处理。该模糊控制器输出参数为农机转向角n，式（17）为三者的模糊关系：

式中，δ为模糊控制器的修正因子，消除位置偏差和航向角偏差的侧重不同，对于行间行驶农机，应更加关注位置偏差的修正，因此δ的取值应适当加大。

该模糊控制系统是一个双输入单输出的模糊控制器；根据控制过程相关专家经验对输入输出进行量化并总结出7×7 条模糊语言规则，其模糊控制规则见表2：

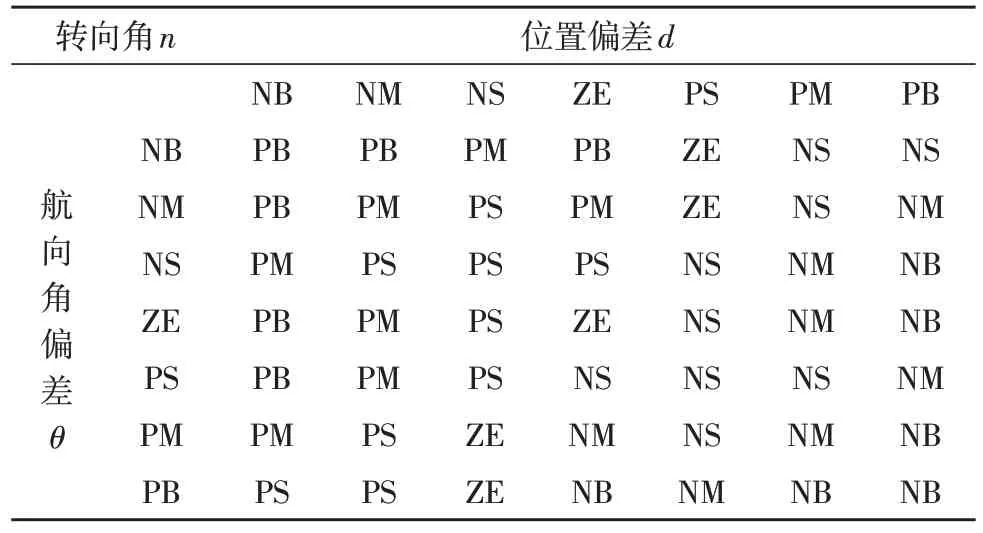
表2 模糊控制规则表

1）航向角偏差θ

基本论域：[-30°,30°]；

量化等级：{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}；

量化系数：Kθ=6/30=0.2；

2）位置偏差d

基本论域：[-30 cm,30 cm]；

量化等级：{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}；

量化系数：Kd=6/30=0.2；

3）转向角n

基本论域：[-30°,30°]；

量化等级：{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6}；

量化系数：Kn=6/30=0.2。

根据所建立的模糊控制规则表，此系统内三个变量位置偏差、航向角偏差和转向角的模糊集合为{负大，负中，负小，零，正小，正中，正大}={NB,NM,NS,ZE,PS,PM,PB}。转向角n的Gauss 隶属度函数如图5 所示。

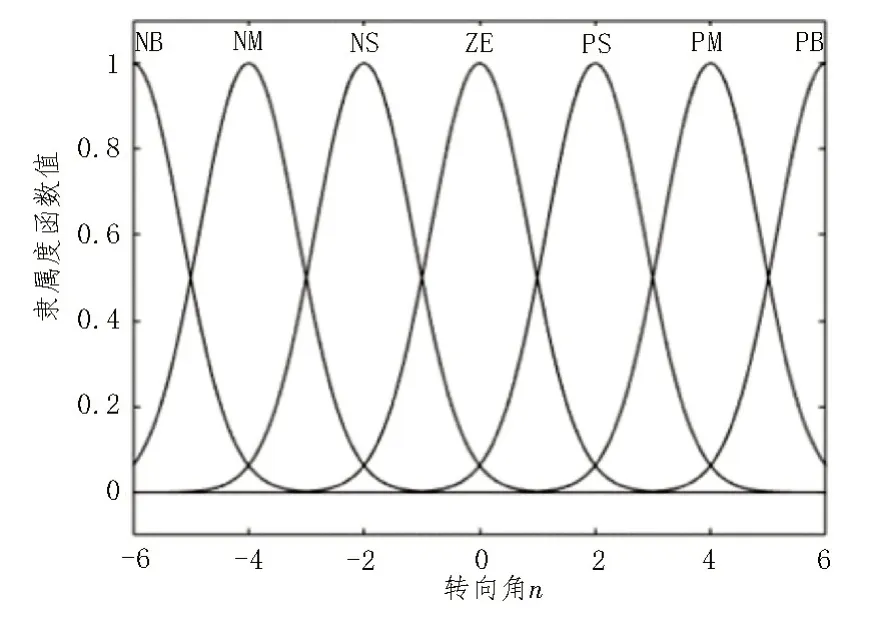
图5 转向角n隶属度函数

采用面积重心法进行解模糊，面积重心法是取隶属度函数曲线与横坐标围成面积的重心，作为模糊推理的最终输出值，相较于其他解模糊化方法，面积重心法具有更平滑的输出推理控制。即使对应于输入信号的微小变化，输出也会发生变化。其数学表达式如式（18）所示：

当农机位置偏差d=-6 且航向角偏差θ=-6°时，转向角n=5.09°。在对基本论域进行量化等级后，在[-6,6]的范围内调节航向角偏差和位置偏差，即可通过解模糊推理获取。

4 自行走控制系统的运动仿真

利用Matlab 对农机行间自行走模糊控制算法进行仿真验证，仿真时设定将y=x的第一象限角平分线作为行间自行走的中心线即预定行驶路径，仿真的初始位置设为（0,0）处，y＞x部分作为行间中心线左侧，y＜x部分作为行间中心线右侧。

图6 的（a）-（c）为农机车身位置偏差d和航向角偏差θ几种典型取值下的运动仿真模拟。

图6 农机行间自行走运动仿真

结合式（17）的模糊函数表达式可知，农机行间自行走策略以消除农机车身位置偏差为主，δ的取值适当选择较大。当位置偏差和航向角偏差均处于正大NB 或负大PB 时，农机需要快速进行行间车身位置调整，此时电动农机需要较大的转向角n，根据文中建立的模型和公式，此时农机左右两侧的履带速度差增大以向农机提供更大的转向角度。当位置偏差处于正小NS 或负小PS 但航向角偏差处于正大NB或负大PB 时，此时农机不需要过多的车身位置调整，只需要及时对航向角偏差进行修正。当农机航向角偏差为零ZE 但存在位置偏差时，也应该及时对农机车身位置进行调整。

5 自行走控制系统的硬件设计

设计的自行走控制系统安装在小型电动履带式农机以便更好地将农机与农艺相结合，目前国内的作物种植大多数采用宽窄行种植技术[15]，大多数通过宽窄行种植的农作物其窄行宽度一般处于35～50 cm范围内，窄行不适宜行走，而宽行的宽度一般根据农作物种植农艺的不同大体在90～130 cm 之间。所采用农机长160 cm，宽66 cm，高45 cm，选用橡胶履带更适宜在复杂的田间环境行驶。

该农机动力由48 V/800 W 无刷直流电机提供，电机驱动相较于传统的燃油发动机驱动，无刷直流电机的结构相对封闭，适宜在农田等恶劣环境下使用。其额定电流为20 A，额定扭矩为5 N·m，额定转速为25 r/s。根据式（19）力矩公式计算单个电机产生的力：

直流电机轴直径约为0.008 m，则力臂为电机轴的半径为0.008/2=0.004 m，根据式（19）得到单电机产生的力约为1 250 N，代入重力系数算得：1 250 N/(9.8 N/kg)≈128 kg，其农机整体承受负载的质量约为250 kg。

电动农机采用58.2 Ah 的铅酸蓄电池作为动力源。电机输出功率计算如式（20）所示：

式（21）为电池放电，其中FAH 为电池放电时间，ZL 为电池放电电流值，NAH 为电池容量，0.85 为蓄电池放电效率，结合式（21）算得农机田间作业最大行驶距离约为7.5 km：

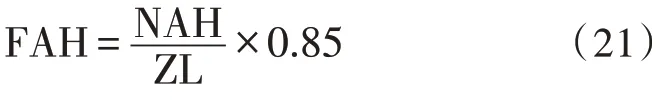
图7 所示为超声波车身检测系统电路图。超声波传感器选择DJLK-003 收发一体超声波模块，平面小角度测距，工作的温度范围为-15～+60 ℃，探头具备一定的防尘防水等级，适用于潮湿、恶劣的测量环境。通过RS485 协议发送车身位置距离值，RS485总线抗共模干扰能力强，最大数据传输速率可达10 Mbps，设置不同从机地址可同时采集四组距离值。

图7 超声波车身检测系统电路图

农机的行间自行走控制系统通过STM32 芯片对农机车身距离值进行解算后向电机驱动器发送调速电压。由上文可知，农机差速转向方式选用独立式差速转向，因此通过减法电路与前进电压信号相减。行间作业时，由调速旋钮电路持续向两侧电机驱动器输出恒值为0～5.0 V 的调速电压。当农机行驶位置偏离行间中心线时，主控芯片接收四组超声波传感器测量值后将位置偏差和航向角偏差作为输入量，经模糊解算后输出农机转向角度，再根据转向模型将-30°～30°农机转向角转换为左右履带的速度差值；通过STM32 的D/A 输出0～2.4 V 的电压值，与调速旋钮电路输出电压值相减输出至近转动瞬心侧的电机驱动器，单侧履带速度降低。其电路原理图如图8 所示。

图8 行间自行走控制系统电路图

如图9 所示对农机行间自行走控制系统进行Multisim14.0 电路仿真，调速旋钮电路采用10 kΩ的分压变阻器向电机驱动器输出0～5 V可调电压信号控制农机行间自行走时的前进速度；STM32的DAC为电压输出模式，可直接作为信号源，利用两个10 kΩ的分压变阻器模拟双路DAC 输出0～2.4 V 差速转向电压信号。当控制芯片通过解算判断农机需要转向修正前进方向时，PA4或PA5输出一个转向角度所对应的电压信号，经过前级电压跟随电路后与调速旋钮电路输出的直行电压信号通过LM358N 电压减法电路相减，再将该电压信号经二级电压跟随电路输出至电机驱动器，左右两侧电机驱动器根据双路D/A 输出的不同而形成电压差值；一侧电机驱动器驱动电压降低，另一侧电机驱动器驱动电压不变，即近转动瞬心侧的速度降低，远转动瞬心侧速度不变，农机修正车身偏差。仿真时PA5控制左转向，PA4控制右转向，调速旋钮持续输出3.0 V电压信号模拟农机前进速度，当PA5处DAC产生1.2 V模拟电压信号时，向两侧电机驱动器分别输出1.8 V 和2.97 V 电压信号，左侧电机转速降低，右侧电机转速不变，农机行驶路线向左侧修正[16]。

图9 Multisim14.0电路仿真图

6 试验及分析

上文分别对行间自行走模糊控制策略和自行走控制系统电路进行仿真测试后，对农机进行田间实机测试。选择在山西省大同市云州区黄花菜种植实验基地实验田进行试验，其宽行宽度约为1.3 m。黄花菜作为一种经济型作物，其采摘过程较为繁琐，需要劳动者行走在行间进行采摘。

通过对人工黄花菜采摘作业的研究获得最佳农机行驶速度约为0.83 m/s，在此速度下农机进行单趟距离为500 m 的采摘作业，耗时约为10 min，则20 min即可完成双人4行黄花菜采摘，其效率约为5 min/行；对比人工步行采摘，双人可同时采摘4 行黄花菜，但此时人工采摘步行速度约为0.3 m/s，则在人工步行采摘模式下，单趟距离为500 m 的采摘作业耗时为30 min，其效率约为7.5 min/行。通过试验得：采用农机行间自行走对黄花菜进行采摘时效率提高约30%，小型电动农机的使用不仅不会对作物和土地造成较大破坏，还大幅度减轻农民的劳动压力，优化农民的工作条件等[17]。

如图10 和11 所示为单次黄花菜采摘作业时四个传感器的距离采样值，其中Echo1、Echo2、Echo3、Echo4 分别为左前侧、左后侧、右前侧、右后侧的超声波传感器距离采样值；图12 为传输至电机驱动器的左侧调速电压Vleft和右侧调速电压Vright的曲线。传感器测量值受复杂外界环境干扰，对于农机行驶姿态和路径的判断困难，位置偏差和航向角偏差都较大时，农机会对路径进行修正，且此时调速电压变化幅度也较大，以便快速修正，在距离采样值波动幅度不大的情况下默认为行间复杂的作业环境因素干扰。试验结果表明：在500 m 的无干预农机自行走作业测试中，农机位置基本位于行中心线上。

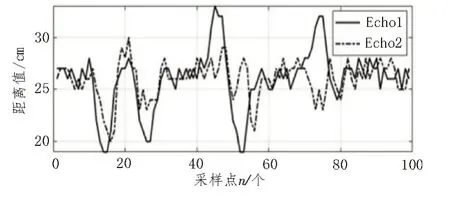
图10 左侧前后传感器距离采样值

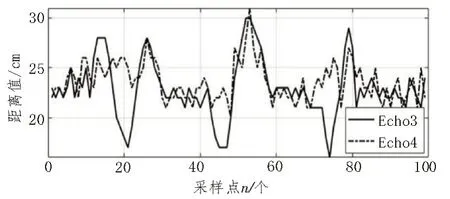
图11 右侧前后传感器距离采样值

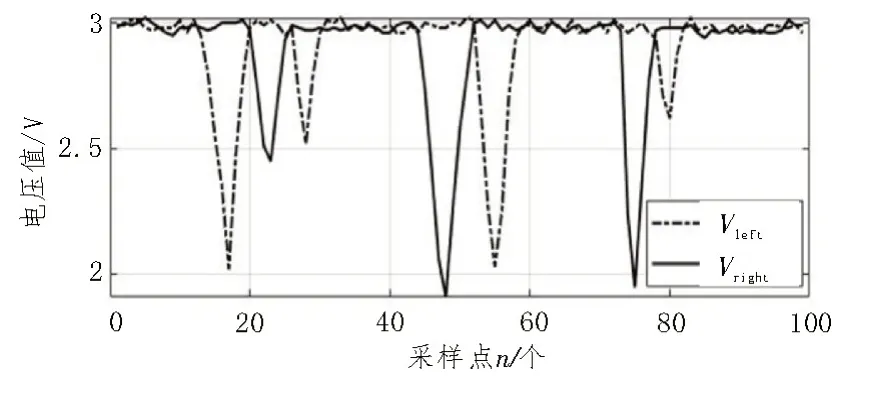
图12 左右电机驱动器调速电压值

7 结论

该文所设计的基于超声波测距的电动农机行间自行走策略旨在优化诸如黄花菜采摘等人工农业生产采摘方式，农机的智能化极大程度减轻农业生产者的劳动强度。通过距离传感器和微控制器实时对农机行间行驶姿态进行判断和修正，即使在复杂多变的田间环境下实机试验，在不需要人为驾驶干预的情况下保证农机沿着行间道路行驶，解决了在大型农机无法进入田间作业时仅能依靠人力进行农业生产的现状，未来可对该款农机进行多种改装后，使其可承担农作物采摘、行间载人及农产品运输、行间植保喷药等任务。