基于层次聚类的共享单车维修点规划模型

毛昊迪，汤鲲

（1.武汉邮电科学研究院，湖北武汉 430000；2.南京烽火天地通信科技有限公司，江苏南京 210000）

在绿色交通大力发展的现在，以“最后一公里”为设计目标的共享单车系统越来越盛行。早期由政府牵头设立的共享单车系统有着固定的停车点位，因此维修点设置之后在很长一段时间内都不会发生变化。随着互联网的发展，在2014 年出现了通过手机扫码使用的共享单车，这类共享单车会根据时间和城市地形形成短期的聚集点。因此如何设置维修点是一个很重要的问题。

国内外对于共享单车的研究主要集中在共享单车的投放[1]、调度[2]，回收[3]和骑行数据的分析[4]上，对于维护确少有涉及。层次聚类算法是一种常用的无监督学习算法，具有简单、结构明了的优点。通过层次聚类算法可以有效地将相近的共享单车聚集点聚集成一个簇，每个簇的聚类中心即为维修点的坐标。单纯的层次聚类算法容易受到局部最优解的影响，已有的解决方法通过剪枝[5]和引入随机矩阵来避免局部最优[6]。蚁群算法是一种启发式全局优化算法[7]，这种算法通过引入随机值来解决局部最优问题。根据蚁群算法，该文提出了一种使用蚁群算法机制的层次凝聚聚类方法，该聚类方法通过使用蚁群算法的信息素机制和随机选择机制来选择聚类方向，通过迭代运算的方式避免出现局部最优解。实验结果表明，相对于层次聚类和k 均值聚类，该算法的聚类效果提升了10%～20%。

1 模型构建

大数量的共享单车会围绕地铁站、公交站、公园入口等地点自发聚集，由于城市地形问题，这种聚集点的分布通常是无规律的。对于无规律元素，可以使用无监督学习方法进行处理，因此聚类算法就是一个非常好的选择。该文基于层次凝聚聚类(AHC)和蚁群算法(ACO)构建规划模型，该模型以凝聚层次聚类为主，通过引入蚁群算法的随机性和迭代机制来减少局部最优解的影响，从而在分布无规律的共享单车聚集点中找到设置维修点的最佳位置。

1.1 层次聚类

层次聚类是一种非常直观的聚类方法。通过一层一层的合并，从下而上或者从上而下一步一步将距离相近的簇进行合并，最终形成一个树状结构[8]。

凝聚层次聚类通过各个元素的邻近度矩阵来计算簇间的距离，从而将距离最近的两个簇进行合并。

邻近度矩阵通常有三种计算方式：

1）单链：两个簇中最近点的邻近度。

2）全链：两个簇中最远点的邻近度。

3）组平均：以两个簇中所有点间的平均邻近度作为两个簇间的邻近度。

前两种方法能够在一定程度上减少噪声点对于合并过程的影响，提高聚类的准确度，对于该文而言，每一个共享单车的聚集点都要考虑在内，因此对于两个簇使用所有点间距离的组平均作为邻近度的计算方式。计算公式如下：

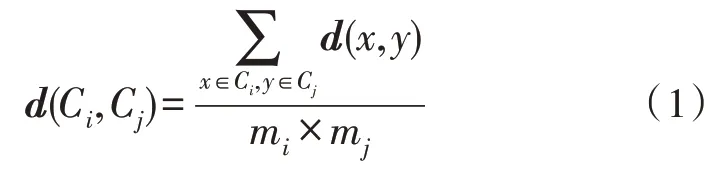
其中，d为邻近度矩阵，C为簇，m为簇中元素的数量。

1.2 蚁群算法

蚁群算法是在1991 年由意大利学者提出的模拟蚂蚁觅食行为的一种优化算法，蚁群算法在很多地方都有应用，如路径优化[9]和电流过载保护[10]，对于聚类算法，蚁群算法同样可以起到优化的作用[11]。

蚁群算法的核心机制是信息素浓度机制和概率状态转移机制，转移概率由与距离成反比的启发式信息和与环境相关的信息素浓度来决定。转移概率计算公式如下：

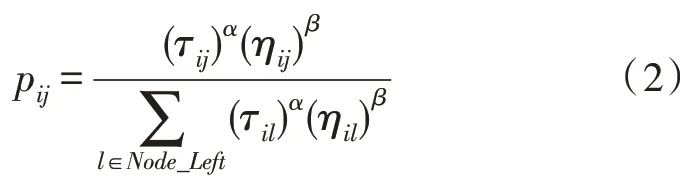
其中，τ为信息素浓度；η为启发式信息，与距离成反比；α为信息素浓度因子，α越大，搜索路径的随机性就越小，α越小，蚁群搜索的范围就越小，越容易陷入局部最优；β为启发式信息因子，β越大，蚁群就越容易选择局部最短路径，β越小，蚁群选择路径的随机性就越大。

在每一只蚂蚁走完一步后，就会对路线上的信息素作更改，信息素变化公式如下：

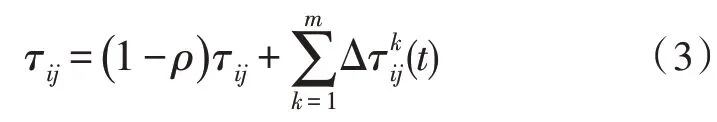
其中，ρ为信息素挥发因子，ρ越小，算法的收敛速率就越慢，ρ过大时，有效路径就有可能被排除掉，影响最佳路径的选择。为第k只蚂蚁从i到j时释放的信息素，通常与i到j的距离成反比。m为蚂蚁的个数，蚂蚁数量越多，得到的最短路径就越准确，但是同时算法时间复杂度就越高[12]。

1.3 基于蚁群算法的层次凝聚聚类

新的算法基于蚁群算法中的信息素机制和概率状态转移机制进行设计，通过引入随机变量来避免局部最优的出现。通过将两个簇的合并看作蚂蚁从一个点移动到另一个点的过程来引入随机变量，最后通过模仿蚁群算法的迭代及目标函数选择出最佳聚类方案。

对于该文需求而言，每个元素的位置信息都应该被考虑在内，因此聚类结果的好坏应该对每个点的位置都进行判断，为了突出位置信息的影响，且保证每个维修点到所管理的聚集点的距离应该尽可能短，目标函数如下：

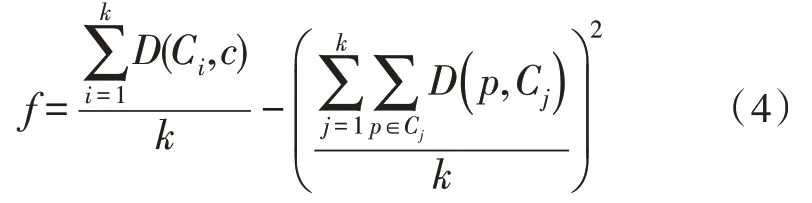
其中，Ci为第i个簇的质心；c为所有元素的质心；Cj为第j个簇；D为欧式距离；k为聚类完成后簇的个数。聚类完成后，当各个簇的质心到所有元素集合的质心的距离越远，且每个簇中的元素到该簇的质心的距离越近，则聚类效果越好。聚类问题被转化为求得最大目标函数的问题。

在进行聚类时，不仅只考虑位置信息，同时还要引入信息素浓度和概率随机机制。参考式（1）与式（2），提出了新的转移概率如下：

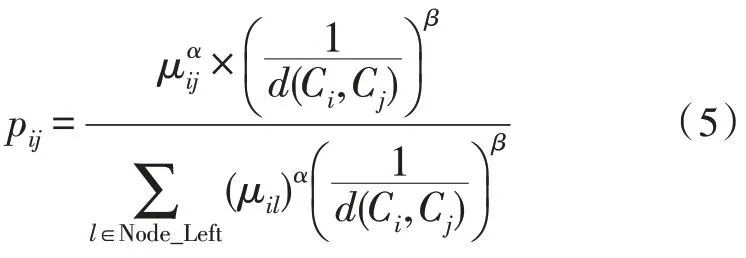
其中，μij为簇i和簇j间的平均信息素浓度，计算公式如下：

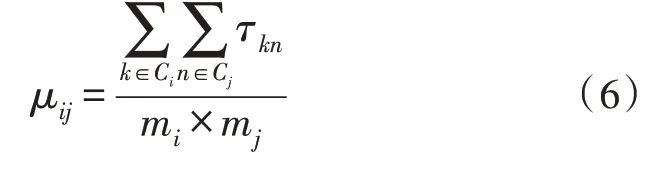
其中，τkn为点k与点n间的信息素浓度。

算法中需要的参数有蚂蚁数量m、信息素浓度因子α、启发式信息因子β、初始信息素浓度τ0、迭代次数r、信息素挥发因子ρ，算法步骤如下：

1）对于k个点，将每个点视为一个簇，根据式（1）计算邻近度矩阵，设置初始信息素浓度矩阵。

2）将m只蚂蚁随机投入到k个点中。

3）随机选一只没有移动过的蚂蚁，根据邻近度矩阵和信息素浓度矩阵使用式（5）来计算合并概率。

4）使用轮盘赌的方式选择合并的簇，如果所有的蚂蚁都移动过一次，则根据式（3）更新信息素矩阵并返回，执行第2）步，如果合并后剩余簇的数量大于期望值，则返回，重新执行第3）步。

5）根据式（4）计算目标函数。

6）根据式（3）更新信息素矩阵。

7）与当前保存的局部最佳目标函数值对比，输出局部最佳目标函数值和最优合并方案。

8）若迭代次数少于r次，则返回，执行第2）步。

9）输出全局最佳目标函数值和最优合并方案。

在聚类的过程中，为了避免蚂蚁出现回环现象，要求每只蚂蚁都只能向没有爬到过的点移动，因此对每只蚂蚁都建立一个禁忌表[13]，表中储存的是还没有爬到的点，当所有的点位都被爬到后，重置禁忌表。

算法中的参数选择需要根据实际应用进行调整，参数的选择会直接影响聚类结果的好坏[14]。对于元素数量较少的数据，一般蚂蚁数量/元素数量为1.5[15]。

2 数据集与实验设置

由于共享单车的聚集点受到地形、公共交通点位置等的影响，而UCI Iirs 数据集中有一类与其他两类线性无关，故实验使用了西雅图2015 年自行车租车行公开的租车点位置信息数据集D1和UCI Iirs 数据集两类作为测试数据集。

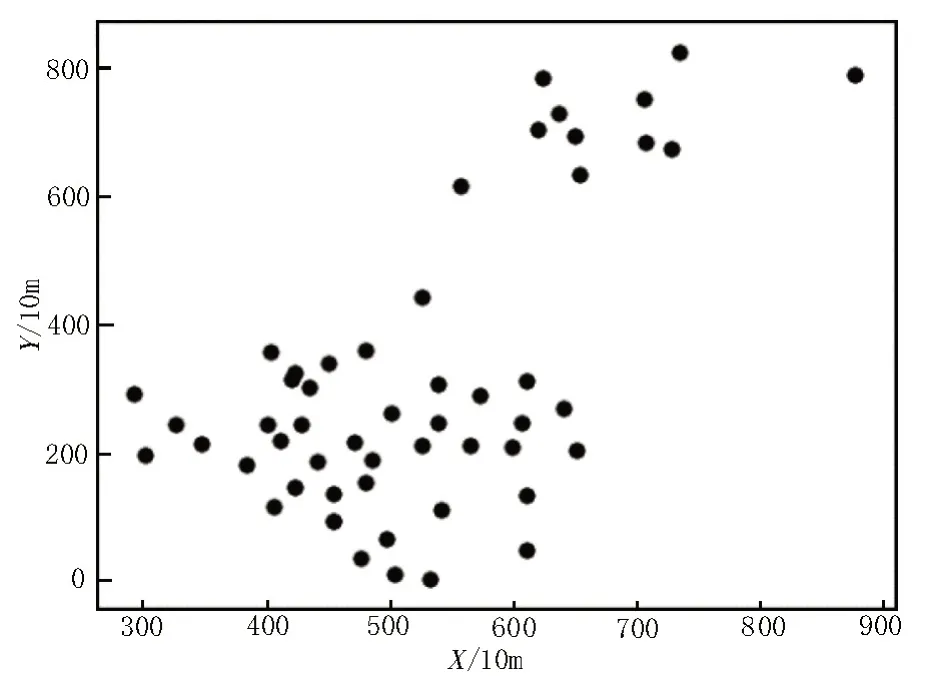
图2 西雅图车站数据集D1

UCI Iris 数据集的数据维度为四维，需要对数据集做一定的处理[16]，UCI 数据集采集的主要是鸢尾花的花瓣和花萼的长宽,共三种鸢尾花，观察发现可以根据花瓣和花萼的面积大小将其分为两类，因此，对UCI 数据做特殊处理：使用花瓣、花萼的面积作为新数据集的特征，将类数由三类合并成两类。以降维后的UCI 鸢尾花数据集来模拟特殊地形导致共享单车聚集点出现隔断式分布的情况。

以经纬度为（47.598 488，-122.390 785）为坐标0 点，以500 m 作为比例尺，代入西雅图的53 个车站点位，最终得到了一个二维数据集D1。

处理后的两种数据集如图1-2 所示。

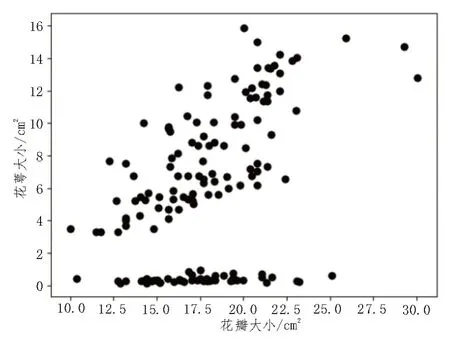
图1 UCI Iris数据集

处理后的两种数据集特征如表1 所示。

表1 数据集特征表

经过多次实验，最终选定实验参数如表2 所示。

表2 参数设置表

3 实验结果与分析

为了体现算法的提升效果，最终选定常见的采用组平均规则的层次凝聚聚类和k-means 聚类作为参考进行对比。在设置聚类簇数为2 时，运行20 次后求平均值。对比结果如表3 所示。

表3 聚类准确率

由表3 可知，当聚成两类时，在西雅图车站数据集上，三种聚类方法的效果区别不大，该文算法的准确性略高于k-means 算法，与普通层次凝聚聚类相近。但是在降维后的Iris 数据集上，由于右上角三个噪声点的存在，基于组平均的普通层次凝聚聚类完全无法区分出两种大小的鸢尾花，聚类效果较差；由于引入了随机和迭代机制，该文算法的准确率提高了10%，与k-means 的准确性相近。

该文中，实际只聚集成两个簇意味着只设置两个维修点，两个维修点并不一定能满足实际需求，因此追加对数据集D1聚类成三类以及四类的实验，此时使用簇中元素到聚类中心的平均距离代替聚类准确率来判断聚类结果的好坏，公式如下：

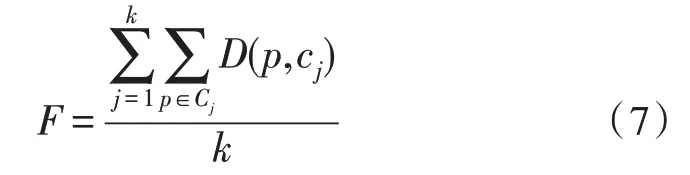
运行20 次后求平均值，实验结果如表4 所示。

从表4 中可以知，对于处理过的Iris 数据集而言，聚集成四个簇时，k-means 算法略优于该文算法，聚集成三个簇时则相反，这是因为该文算法无法对Iris 数据集的右上角的三个噪声点进行处理所造成的；但在西雅图车站数据集上，该文算法相比AHC和k-means，各个元素到聚类中心的距离减少了10%。

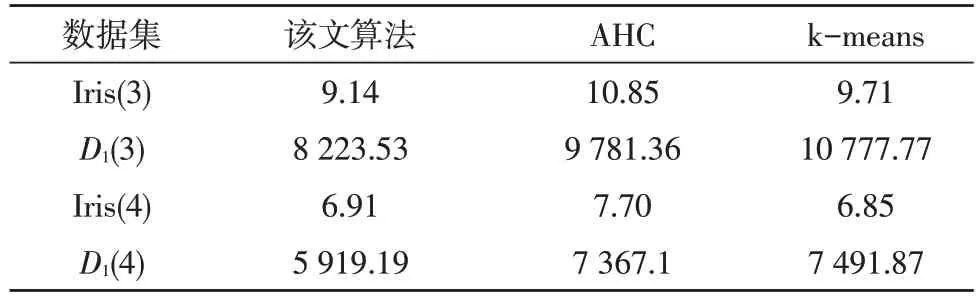
表4 聚类效果

4 结论

该文提出了一个基于蚁群优化和层次凝聚聚类的共享单车维修点规划模型，通过使用信息素机制和概率状态转移机制对聚集点进行聚类操作，聚类中心即为维修点的位置。

根据实验结果显示，该文方法在所有情况下优于AHC 算法，在绝大多数情况下优于k-means 算法，使用该方法规划的维修点位置到各个点位的平均距离减少了10%。