近朱者赤，近墨者更黑——教育中的非对称同伴效应研究

王春超 肖艾平 于瀚辰

(1.暨南大学 经济学院，广州 510632；2.广东金融学院 保险学院，广州 510521；3. 哈佛大学 地理分析中心，美国马萨诸塞州)

一、引 言

2017年底，世界银行发布的《2018年世界发展报告:学习以实现教育的承诺》指出：“目前全球教育系统正面临‘学习危机’，中低收入国家的基础教育效果与中高收入国家的差距正在逐步拉大。在中低收入国家平均认知能力排名前25%的学生，还不及中高收入国家排名末尾25%的学生。”[1]这种在基础教育阶段因“学习危机”所产生的弱势地位，将会继续扩展到儿童成年后的劳动力市场中，进而转化为“技能危机”。对农村基础教育阶段儿童而言，学校教育是其人力资本积累的主要途径，儿童早期的人力资本投资要比晚期的干预重要得多。[2]然而，我国部分农村地区基础教育发展相对滞后，教育产出效率与城市相比，还有着较大差距。[3]因此，提高我国农村基础教育质量，提升儿童人力资本积累的效率，是破解“学习危机”和“技能危机”的基础工程，对实现城乡教育公平有重要意义。

现有文献从学校规模、师资建设、家庭背景等多方面对教育质量进行了研究[4-5]，科尔曼(Coleman)等人[6]发现相比学校投入，影响学生成绩最主要的因素是家庭背景，其次是同伴效应。然而许多农村儿童的父母外出务工，只能将学龄孩子留在家乡由隔代老人或其他亲人代为照管，父母在儿童学习成长中长期缺位。[7]此外，农村基础教育阶段的学生年龄偏小，正是各种观点形成期，同班同学由于绝大部分时间在一起学习生活，因此同伴在儿童成长过程中至关重要。[8-12]

然而，由于班级同伴效应的混合效果较难评估，现有文献多基于同伴之间知识溢出理论[13-14]，探讨如何以最佳知识溢出方式，通过同伴分配和重组来提升整体学业成绩。具体概括为两类文献，一类是“近朱者赤”，即将成绩差的学生从成绩较差的同伴群体转移到成绩较好的同伴群体中，他们的成绩可能会提高；[15-16]另一类是“近墨者黑”，成绩较差的同伴也可能因其不良行为表现对成绩好的学生产生负外部性[17-19]。那么，在同一个同伴群体内，高分群体的正溢出效应与低分群体的负溢出效应是否对称？如果不对称，两者综合博弈后的结果是变大、变小，还是相互抵消？以往研究缺乏对班级同伴进行分配和重组后的总体效应估计。随着空间计量理论和应用的发展，大量文献认为空间距离的邻近会增加学生网络之间的互动，进而产生同伴效应[20-21]，但网络互动固有的内生性使同伴效应识别存在困难，空间自回归模型能较好识别网络中的情境效应、内生效应和相关效应[22-23]，只有当学生相互接近并产生社会互动时，空间邻近上的同伴效应才会产生[14]。因此，研究学生在班级中的同伴效应，不容忽视的是空间上的邻近性，而以往文献较少考虑班级同伴空间距离与同伴效应的关系。

本文的主要贡献：第一，克服了以往文献的单向分析视角，重点考虑同伴在班级网络互动中的双向特点，为全面理解同伴效应的特征做出了贡献。第二，用空间计量方法较好解决了同伴效应估计中因自选择而产生的内生性问题，有助于更精准识别同一群体中的非对称同伴效应。第三，运用了一个学年的跟踪数据，考察班级中非对称同伴效应的动态变化，并对比不同学业水平的同伴在空间模拟排座后的平均成绩，扩展了社会网络中空间距离与学生成绩关系的研究。

二、文献评述

近几年研究同伴对学生教育结果影响的文献非常丰富，范围涉及社区、学校、年级、宿舍、班级、小组等，研究主题也十分广泛，从教育中同伴效应的非对称角度看，可总结为以下三类文献。

(1)“近朱者赤，近墨者黑”的同伴效应。 “近朱者赤”认为学生处在优秀的同伴中，能获得更好的资源、地位和成就，优秀同伴对学生的教育结果有积极影响[12]，影响机制是优秀同伴通过课堂互动给其他学生带来积极的示范[15]。“近墨者黑”考察了同伴不良行为对青少年的负面影响。这种负面影响是差生的破坏性行为和花费教师更多时间维护课堂秩序造成的。[24]卡雷尔(Carrell)的研究表明学生周边每多一个破坏性同伴，学生的学业成绩会降低1/14个标准差，违规行为发生的概率增加17%；儿童与破坏性同伴每多接触一年，学生未来收入的当前折现价值会减少8万美元。[18]

(2)能力同伴效应的非对称性。 能力同伴效应可概括为同质与异质影响两类文献。“同质影响”，即学生倾向与具有相同人口学(种族、年龄、性别等)、文化和行为特征的同龄人建立联系。[13]无论对于高能力还是低能力的学生，均受益于与其有类似能力的学生在一起，同质性更强的教室使教师能够针对特定的学生群体定制教材和学习进度。[25]“异质影响”从学生成绩、学科专业、性别等角度得到了非常不同的结论。如很多学者发现班级内的同伴效应较大，也有部分研究认为教育中的同伴效应很小。[26]因此，在同伴效应对学生的学业成绩影响方面，还需要更多细致而深入的研究。

(3)同伴空间距离与学生成绩。 空间距离的邻近会增加学生之间的互动，而互动会促进同伴效应的产生，但空间上的接近只在社会关系较近的学生之间产生同伴效应。[27-28]座位离得越近的学生交互会更多，认知也越积极，空间距离与学生受欢迎程度存在正相关。[8][29]学生的座位位置和学业成绩、课堂表现、注意力、师生交互等都有很强的相关性[21][30-31]，因此班级座位编排可以作为改善学生关系的工具，但具体怎样的座位安排与学生间的社会关系有联系并不明确。

综上，目前的文献空缺主要在三个方面：第一，同一群体中同伴效应的影响是相互的，对同群体学生之间网络互动的总体效应还缺乏研究；第二，不同特征同伴群体的影响是不同的，而异质性的非对称同伴效应还有待探究；第三，基于班级学生之间的非对称同伴效应，如何科学合理地编排座位还不够清晰。因此，有必要从同伴效应的双向视角，估计同一群体整体非对称效应。本文通过构造班级学生随机排座的空间权重矩阵，采用空间计量模型分别估计了高、低学业学生的双向同伴效应；并分性别、年级、同桌等情况对非对称同伴效应进行异质性分析。此外，本文模拟了三种不同座位编排方式，对不同学业学生进行座位的最优组合，从而达到班级整体学业成绩的帕累托改进。

三、实验设计

本文使用的数据来自课题组与湖北省Q县教育局开展的联合实地调查实验。我们从全县农村小学中随机抽取了三所小学，选择3～5年级的学生为研究对象(1)由于本实验要求学生填写问卷，对学生的识字和理解能力有一定要求，考虑到实验的有效性，故没有包含1～2年级学生；6年级学生一般面临升学问题，不容易跟踪，故也没有包含这部分学生。，样本共抽取了21个班级共计1 005名学生参与实验，其中男生564人，占比56.12%，女生441人，占比43.88%(2)男生比例过高可能有两个原因。首先，我们选择实验的县，进城务工人员的比例非常高。出于安全考虑，他们更可能带上女儿。其次，受传统观念影响，农村地区男孩出生性别比要高于女孩。。实验时间从2015年秋季学期开始，到2016年春季学期结束，持续了近40周。实验之初，我们要求参与实验的各班班主任提供学生上学期期末成绩、学生花名册及学生身高信息等。第一学期开学前两周，我们对学生进行随机排座并开展第一轮问卷调查。随机排座的方法是：首先，将班级学生按身高从低到高排序(3)按身高分配可避免视线遮挡问题。为消除身高可能与成绩有关的疑虑，本文除了在回归时控制身高外，还用固定效应模型验证了身高与成绩的关系，发现身高对成绩没有显著影响。，再分成若干组，每组占两排座位；如果班级出现奇数排，则第一排同学为第一组，后面每两排为一组。其次，每组学生依次在组内自由抽签确定座位，学生座位保持不变直到期中考试。考虑到学生视力均衡需要，期中考试后每隔两周以两列座位为单位“捆绑式”水平轮换直到期末考试(4)各组之间座位“捆绑式”水平轮换方式具体为：每两周换一次，每两列为一大组，以一个典型教室有四大组为例，第一大组整体换到第二大组，第二大组整体换到第三大组，第三大组整体换到第四大组，第四大组整体换到第一大组，两周后依次类推换座。。整个实验过程中学生在组内的相对座位固定，没有更换座位的报告。图1是典型班级的座位安排。

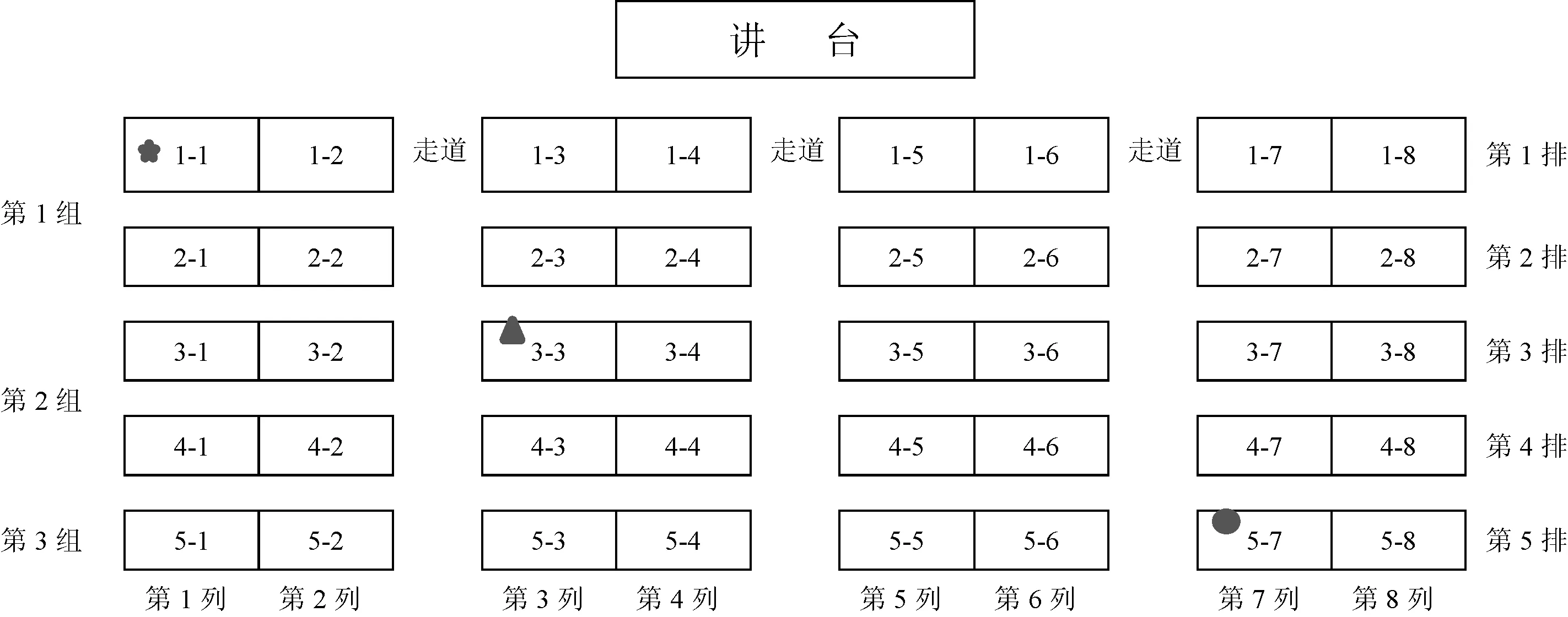
图1 典型班级的座位安排

第二学期开学前两周内，对学生进行第二次随机排座并开展第二轮问卷调查(5)为减弱惯性思维对问卷结果的影响，第二轮问卷在结构上与第一轮相同，但部分内容和问题顺序有差别。。问卷利用学生课堂时间集中填写，由班主任回收后录入到网上问卷系统，信息不完整的问卷需交由学生补充完整后再次录入。整个过程都有研究人员的全程指导与监督，确保数据收集的准确性与有效性。实验流程如图2所示。

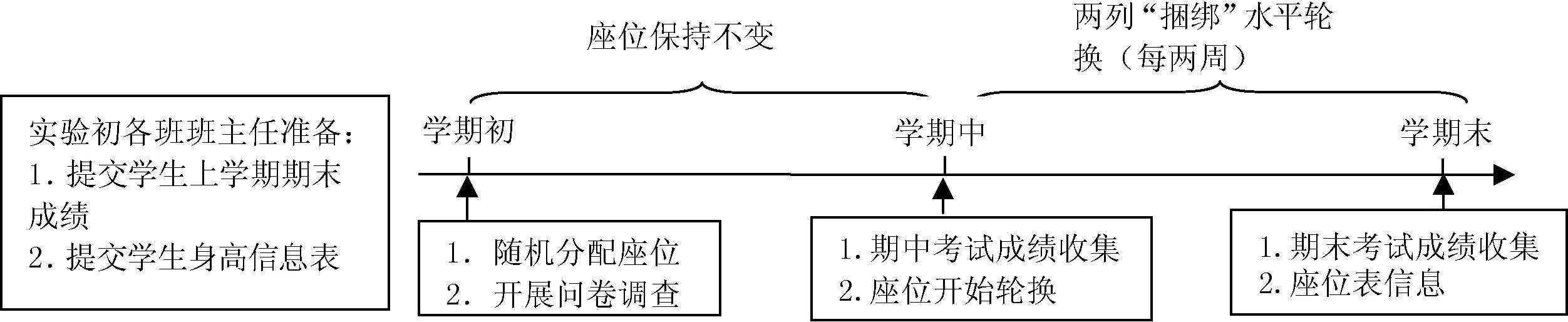
图2 实验流程图

四、数据与计量模型

(一)数据及描述性统计

本文使用的数据主要来自湖北省Q县共计1 005名学生的样本，主要包括三所学校3～5年级(共21个班级)的两轮调查问卷、5次考试成绩和两次随机座位表信息。由于研究对象没有变化，所以两轮调查问卷的问题具有很高的一致性，覆盖了本文研究的变量数据，具体数据及变量的描述性统计如表1所示。

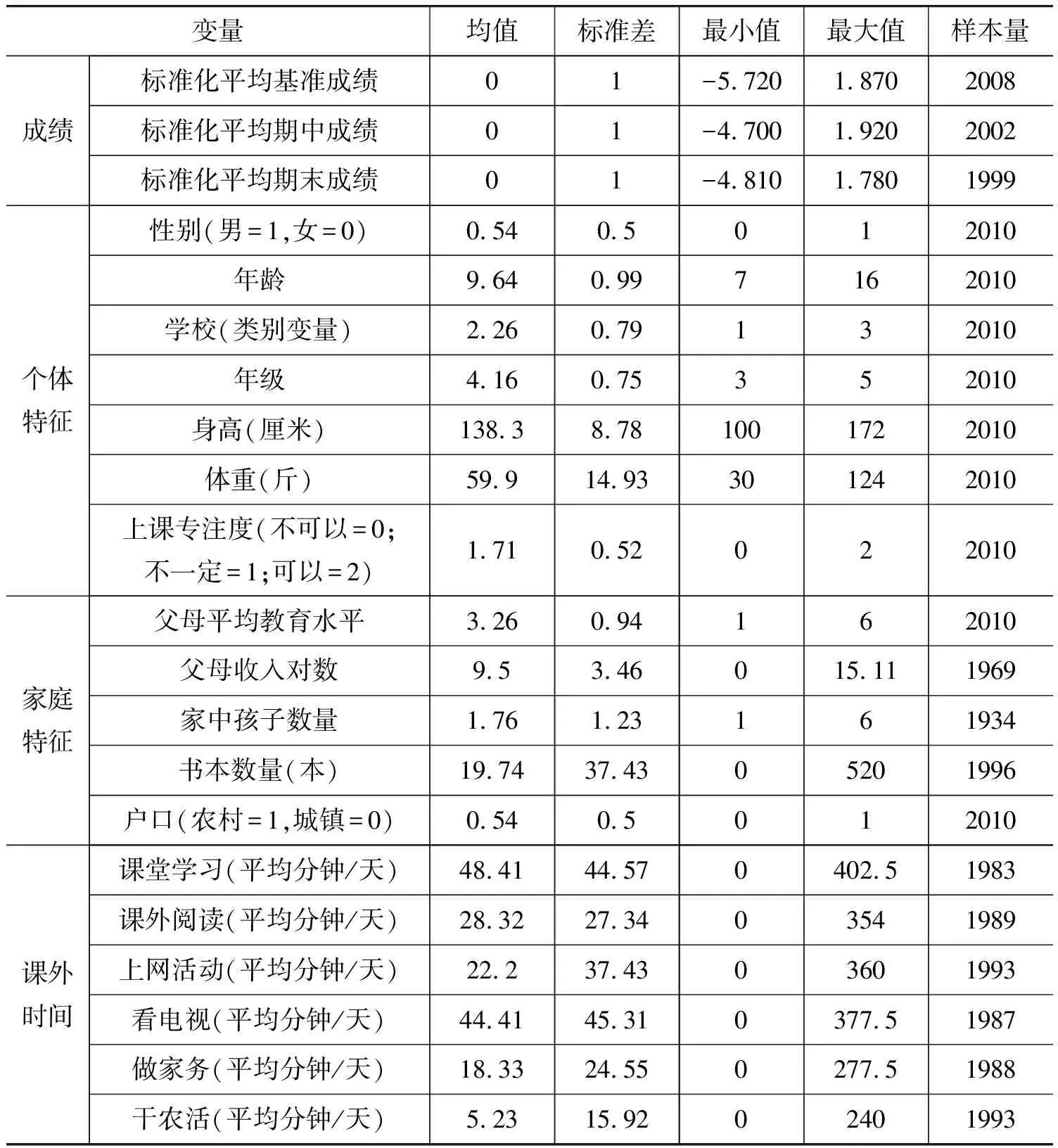
表1 主要变量描述性统计

(二)空间计量模型

1.座位周边同伴的界定

由于班级学生在互动时，更多存在于座位周围，尤其是座位邻近的同学[12]，因此考虑学生座位周边的同伴效应意义更大。本文把学生i的座位周边定义为前后+左右+斜前斜后的同学，因此，学生i座位周边的同学最大值为5人，最小值为3人(6)若学生i坐在最后或者最前排且没有同桌，即一个人单桌，则座位周边同伴为2人。，座位周边学生数如图1所示。若某一学生i的座位坐标是1-1，图1标注五角星形的位置，则他(她)的座位周边同学共有3人，分别为1-2、2-1、2-2；若某一学生i的座位坐标是3-3，图1标注三角形的位置，则座位周边同学共有5人，座位坐标分别为2-3、2-4、3-4、4-3、4-4；同理，若某一学生i的座位坐标是5-7，图1圆形的位置，则座位周边分别是5-7、4-8、5-8这三人了，隔着走道的不计算为周边(7)由于考虑到学生视力均衡的需要，本实验在学生期中考试后以两列为一组，每两周一次的频率，各组之间进行座位“捆绑式”水平轮换直到期末考试，所以期中考试后每大组的位置是不断变换的，学生在隔着走道之间进行固定交流的机会较少，而大组内的成员则相对稳定。。

2.空间自相关分析

本文使用空间计量方法估计同伴对学生学习结果的作用。采用空间模型分析同伴效应前，需检验模型最小二乘回归残差中(学生平均成绩)是否存在空间自相关性。若存在，说明OLS回归不是最优线性无偏估计量，可通过建立空间计量模型消除空间自相关，同时对同伴溢出效应进行估计。空间相关性的检验，采用空间自相关指数Moran’s I[32]，定义为：

(1)

(2)

残差Moran’s I统计量是渐进正态分布的。[33]若Moran’s I 显著，则表示模型中存在显著的空间自相关性，需要使用空间计量方法进行消除。表2是两轮随机排座后的Moran指数检验值，Moran’I的检验均通过1%显著水平的检验，表明两轮随机排座后，模型中存在显著的正向空间相关性，需要使用空间计量模型。

表2 两轮随机排座后Moran指数检验值

3.空间回归模型

空间计量技术在估计社会互动中的应用被认为提供了改进的识别，特别是空间自回归模型提供了足够的信息来识别内生和外生效应[32][34]，因此避免了反向选择的问题。同伴效应在空间上的表现一般为因变量(成绩)的空间溢出效应，为了分别量化高、低学业同伴的非对称同伴效应，本文选择因变量空间滞后模型进行分析，模型设定如下：

Y=ρ1*W1*Y+ρ2*W2*Y+X*b+e

(3)

式(3)Y代表所有学生随机排座后的平均标准成绩；X为控制变量，包括平均基准成绩和学生个体和家庭特征；e为误差项，ρ1、ρ2、b为回归系数。W1、W2为空间权重矩阵，W1中的每个元素设定为：wij=1，表示第i个同学与第j个同学相邻, 并且i同学成绩低于相邻同学平均成绩；wij=0，代表其它情况。W2中的每个元素设定为：wij=1，表示第i个同学与第j个同学相邻, 并且i同学成绩高于相邻同学平均成绩；wij=0，代表其它情况。如果将W1与W2求和即为经典的邻接权重矩阵。本文将经典的邻接权重矩阵分解为W1、W2两部分,W1用于识别高学业同伴溢出效应,W2用于识别低学业同伴溢出效应，W1、W2同时放入一个模型中，即可识别出高、低学业同伴之间的非对称效应。模型采用空间两阶段最小二乘估计(Spatial Two Stage Least Squares,S2SLS)。

五、计量结果与讨论

(一)学生座位周边的非对称同伴效应

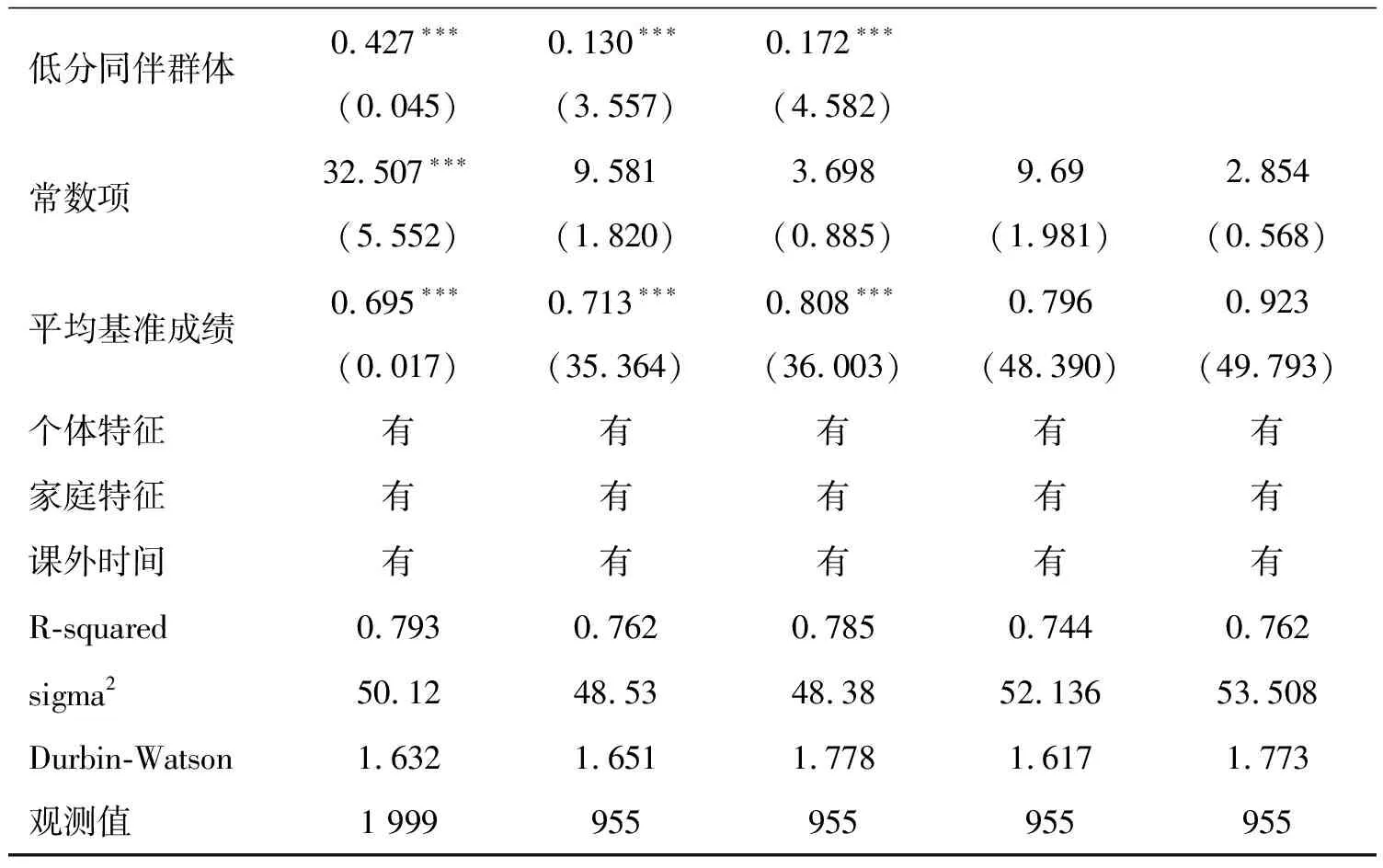
本文把学生座位周边所有同学成绩高于本人界定为高分群体，反之座位周边同学成绩低于本人的界定为低分群体。表3是两轮随机排座后，分别处于高(低)分同伴群体中学生成绩双向同伴效应结果。其中，第1-3列是空间计量模型估计的结果，第4-5列是普通OLS回归的结果。空间计量结果表明，学生成绩会受到周边同伴的显著影响，处于不同同伴群体中的空间效应不同。具体来看，学生处于高分群体中会使本人的成绩显著提高0.155个标准分；若周边都是低学业成绩的同伴，会使本人的成绩显著降低0.427个标准分，即学生座位周边低学业同伴的负向溢出效应大于高学业同伴的正向溢出效应。从两轮随机排座的结果来看，学生座位周边的高学业同伴的正向溢出效应分别为0.076、0.139，而低学业同伴的负向溢出效应分别为0.130、0.172，结果均显著。

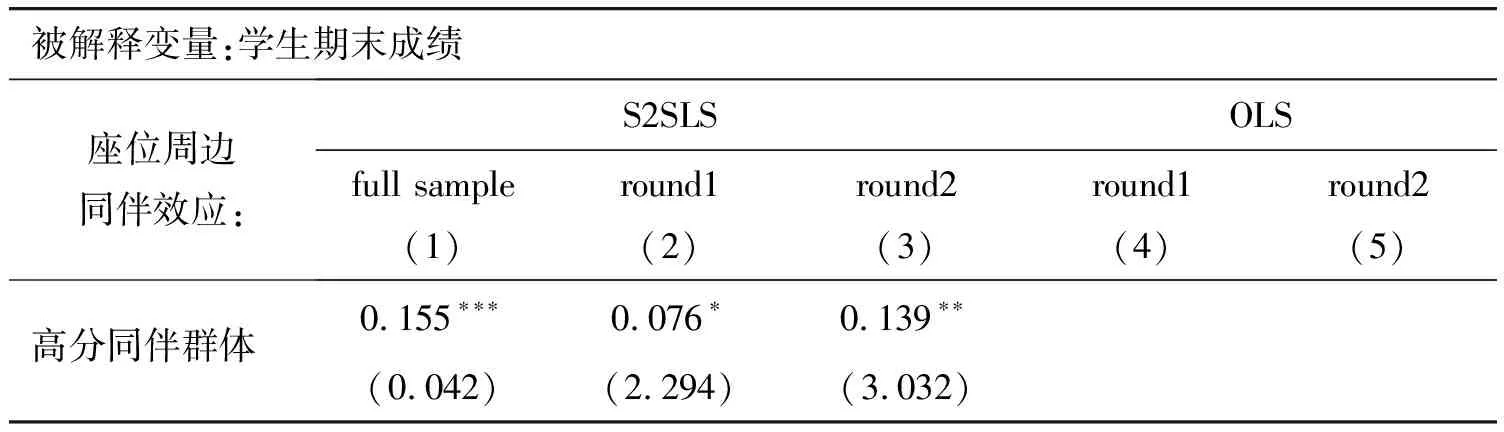
表3 座位周边的同伴效应

续表

这说明学生成绩会受到周围同学平均成绩的影响，但处于高学业群体和低学业群体的影响存在差异。无论处于高学业还是低学业群体中，当周边同伴成绩越高时，会显著正向影响本人的成绩，而周边同伴成绩越低时，会显著负向影响本人的成绩，且存在负向溢出大于正向溢出的非对称同伴效应。

(二)非对称同伴效应的异质性分析

1.不同性别学生的非对称同伴效应

本文控制了学生个体特征、家庭特征和学校特征后，对学生性别的同伴效应进行了空间计量估计。表4的(1)、(2)列是两轮随机排座后男女学生成绩的非对称结果。与表1结果类似，无论是男生还是女生，周边同学的成绩对本人都有显著影响，且低分同伴的负向影响大于高分同伴的正向影响，但不同性别具有异质性。周边同伴的成绩对男生有显著的影响(P1=0.139；P2=0.156)；周边同伴成绩高能显著提高男生成绩，周边同伴成绩低对男生有显著负向影响，且负影响大于正影响。对女生而言，女生显著受到座位周边低分同伴的负向影响(P1=0.119；P2=0.194)；而如果座位周边是高分同伴，女生成绩会有所提高，但提高程度不同。在第二轮排座中，女生的成绩因座位周边高分同伴而显著提高。这也说明，与男生相比，女生更容易受到周边高分同伴的影响。其中可能的解释是女生融入与成功参与学校环境的程度更高，对环境的主观评价度更高。[35]

2.高(低)分同桌的非对称同伴效应

在随机排座后，同桌需保持不变，由于同桌之间的互动更为频繁，因此，相比座位周边其他同伴，同桌对学生成绩的影响会更大。鉴于此，我们考察了高分同桌与低分同桌的非对称效应。表4的(3)、(4)列分别代表两轮随机排座后同桌的同伴效应。结果表明，当同桌成绩高于本人时，对其没有正向的溢出效应(P1=-0.01；P1=-0.014)，当同桌成绩低于本人时对其有负向溢出效应(P2=0.023；P2=0.019)。同桌的这种空间效应小于座位周边的所有同学的平均效应。原因可能是一个学生的成绩不仅受到同桌的影响，也会受到座位周围其他同学的影响，因此可能导致同桌的影响识别存在一定的偏误。

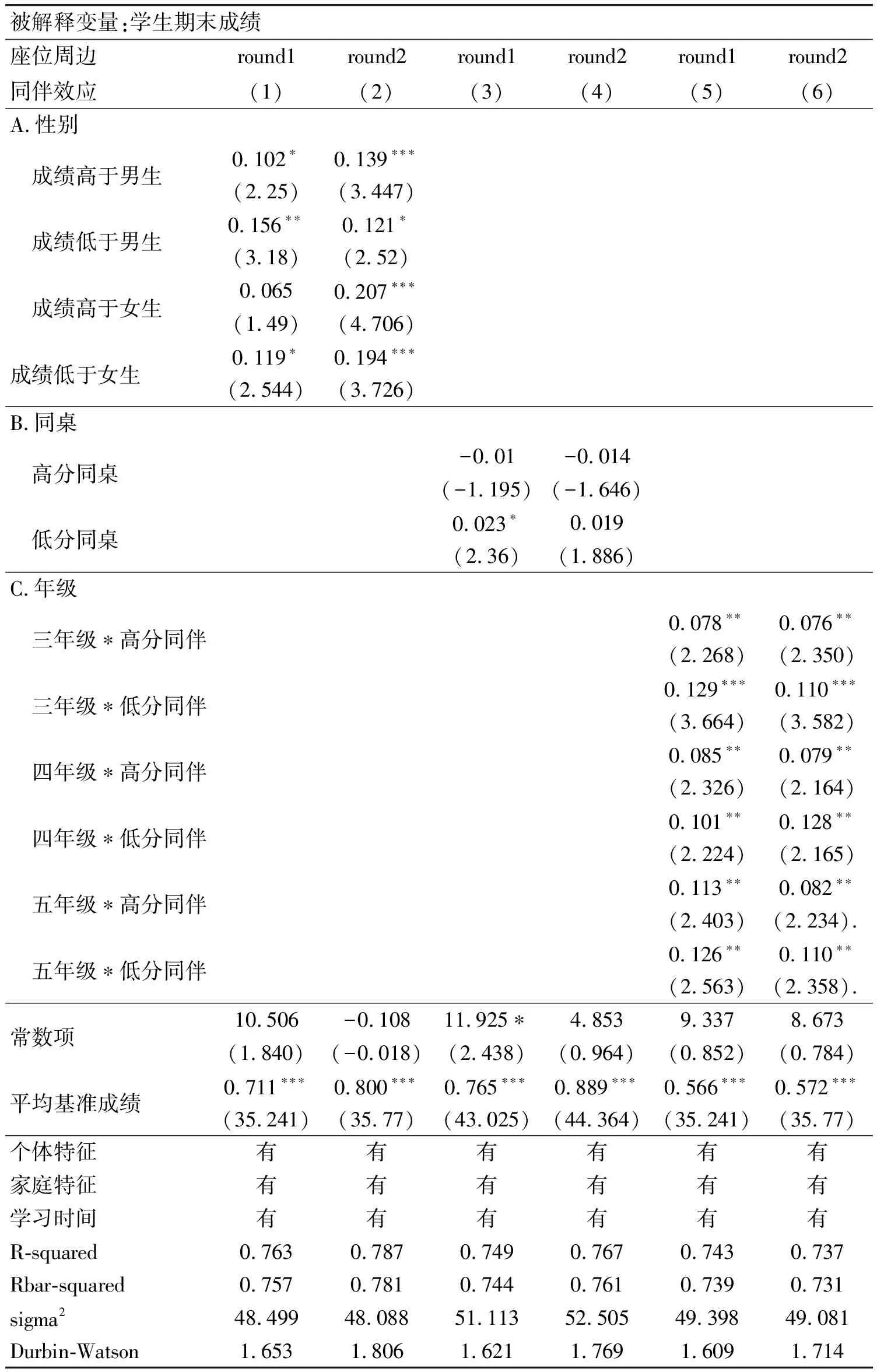
表4 不同类型的同伴效应

3.不同年级的非对称同伴效应

在控制学生个体、家庭和学校的基本特征后，加入了年级和高低分群体的交互项，具体的回归结果如表4的(5)、(6)列所示。整体上看，三、四、五这3个年级的学生均会受到座位周边同伴成绩的显著影响，两轮随机排座共12个回归系数的显著水平最低都是5%，且周边低分同伴群体的负向溢出效应大于高分同伴的正向溢出效应。这与表3中的整体样本回归结果一致。从3个年级内部来看，三年级学生的负向效应更大，即对低年级的学生而言，座位周边是低分同伴的负向影响会显著大于高分同伴所带来的正向影响。一般而言，低年级的学生正处在学习习惯形成的关键期，而低分同伴大多有些不良的学习习惯，因此负向的同伴溢出效应会更大。

六、稳健性检验与排座策略

(一)安慰剂检验

为进一步证实学生i的成绩与邻座周边学生之间存在显著的正向空间相关性，验证学生受到座位周边不同能力学生的非对称影响，本文借鉴安慰剂检验(placebo test)思想[36]，假定学生i与邻座周边以外的学生(任意不相邻的学生)均存在空间依赖性，并随机生成空间权重矩阵后，把随机的空间权重矩阵纳入原模型中求解。

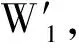
表5 随机空间权重矩阵的估计结果

续表

(二)空间模拟排座

在上文的分析中，我们发现学生会受到周边同伴的影响，处于高分同伴群体与处于低分同伴群体的效应不对称，周边同伴成绩的提高会带动学生本人成绩的提高；同时，周边同伴成绩的下降也会降低学生的成绩，低分同伴的负向效应大于处于高分同伴的正向效应，即 “近墨者黑”的负外部性大于“近朱者赤”的正外部性。由于空间效应存在非对称性，不同的座位分配将会带来差异性的影响。那么，在学生特征既定的情况下，如何对班级座位进行最优分配，才能最大限度地提高班级整体学业成绩呢？

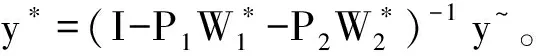
1.高分与低分学生相间排座

如何在学生特征一定的条件下，优化班级整体学业成绩呢？现实中常见的做法是让低分学生与高分学生搭配在一起成为同桌，充分发挥高分学生的正外部性，使其通过良好的学习习惯对低分学生起到榜样和激励作用，进而提高低分学生的学业成绩，达到班级整体成绩的最优化。

本文在这种高低配对的思路下，把班级学生的成绩按从高到低的顺序进行排座，从左边第1列开始排座，第一排的座位座标1-1排第1名，1-3排第2名，1-5排第3名，1-7排第4名；然后第二排的座位座标2-2排第5名，2-4排第6名，2-6排第7名，2-8排第8名，后面均按前述规律进行相间排座。高分学生排好座位后，然后配对同桌，座标1-2排倒数第1名，1-4排倒数第2名，1-6排倒数第3名，1-8排倒数第4名，第二排与前面一样进行相间排座。具体排座见图3。

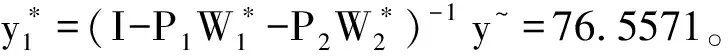
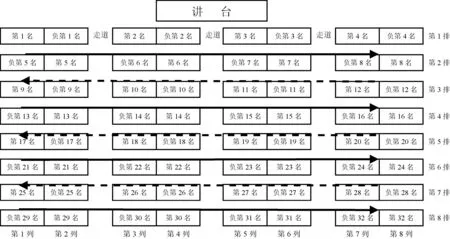
图3 相间排座座位图

2.按高—低分从班级中心到边缘位置的环形排座

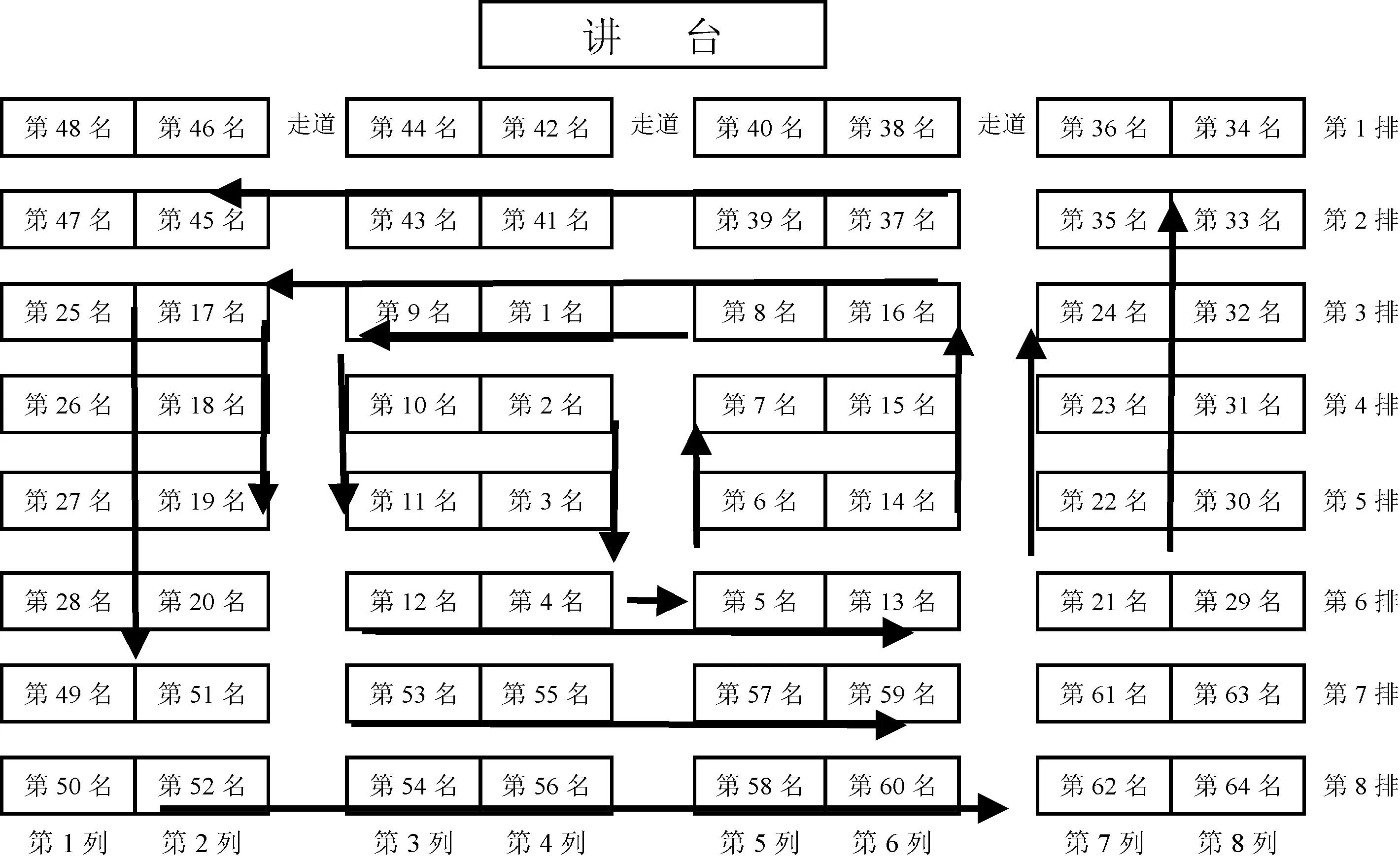
图4 环形排座座位图

3.按低—高分从班级中心到边缘位置的环形排座

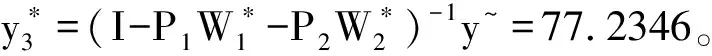
综上分析，本文模拟了三种座位后班级整体平均成绩。表6列出了模拟排座与原始排座后学生平均成绩对比。我们发现，模拟排座后，高低分环形排座的效果比原始随机排座的要好，而高低分相间排座的学生平均成绩低于原始随机排座后的成绩。按成绩低-高升序环形排座后，学生平均成绩是最高的。但在现实排座中，班主任一般会倾向把表现不好的低分学生排在边缘靠后的位置，以避免他们影响到其他学生的学习。而本文通过模拟发现，把低分学生排在班级中心位置，学生的总体平均成绩会更高。可能是一方面低分学生坐到教室中心位置后，周围都是成绩相对比自己好的同学，因此会受到周边高学业同伴的正向溢出效应。另一方面从座位在班级内空间位置的角度看，中心位置将受到来自更多目光的注视，无形中坐在中心位置的学生可能受到的监督更多，因而倾向表现出更好的学习效果。当然，在现实中班主任不可能完全按学生成绩排座，本文结果也只是对不同排座方式的模拟，因此，实际结果还需要现实的检验。

表6 模拟排座与原始排座学生平均成绩对比

七、结论与讨论

本文采用空间自回归模型，定量估计了因座位空间距离的随机变化，学生周边分别是高学业与低学业群体的非对称同伴效应。具体而言，学生周边的高学业同伴成绩每提高1个标准分，本人成绩会提高0.076～0.155个标准分；而低学业同伴的成绩每降低1个标准分，本人成绩会降低0.130～0.427个标准分。在异质性方面，学生的性别、同桌成绩、年级也受到同伴的非对称影响。座位周边高学业同伴使男生成绩提高0.102～0.139个标准分，使女生成绩提高0.065～0.207个标准分；而周边是低学业同伴，使男生成绩降低0.121～0.156个标准分，使女生成绩降低0.119～0.194个标准分。无论男生还是女生，周边是低学业同伴的负向影响均大于正向影响，相比男生，女生受到周边高学业同伴的平均正向影响更大。此外，我们发现高学业同桌没有正向溢出效应，而低学业同桌有负向溢出效应。从不同年级看，三个年级均表现出了一致的非对称同伴效应，其中，三年级低学业同伴的影响更大。

总体来看，本文发现学生会受到座位周边同伴的非对称影响，低学业同伴的负向溢出效应比高学业同伴的正向溢出效应更大，即“近朱者赤，近墨者更黑”。这是因为学生与邻座周边同伴存在空间依赖性，班级座位的邻近会增加同伴之间交流的机会与频率。因此，建议通过优化学生班级座位分配，有效发挥高学业学生的正向知识溢出效应。同时，需多关注低学业学生，适当把他们安排在教室中心位置，使其感受到集体的关注，提高内在学习动力，提升班级整体学业表现，进一步提高农村学生人力资本的投入产出效率。

由于实验条件所限，本文实验得到的结论是随机排座后非对称的同伴效应。为了与原始方案对比，本文分别模拟了按成绩排名进行高低分相间排座、高低分降序环形排座和高低分升序环形排座三种方案。虽然模拟的结果中，高低分升序环形排座，学生的整体平均成绩最优，但还需进行实践的检验。在既定的班级社会网络中，如何对学生进行座位的分配与重组，使同伴之间充分发挥正向的溢出效应，进而使整体学业成绩达到最优，这既是同伴效应研究中的一个难点，也是学校管理者及班主任的现实困惑。本文对比了几种排座方案的结果，在这方面进行了先行探索。研究排座的现实效果，并将研究场景扩展至高等教育乃至成年劳动力的工作场所，将是进一步研究的方向。