低秩稀疏和改进SAM的高光谱图像误标签检测

刘 煊，渠慎明,2*

(1.河南大学 软件学院，开封 475001；2.河南大学 智能网络系统研究所，开封 475001)

引 言

高光谱图像是由成像光谱仪接收的数十上百个波段所反射回来的地物的光谱特性组成。高光谱图像由两个空间维和一个光谱维构成，光谱维中的光谱向量代表了高光谱图像中相应像素独特的光谱特征。由于光谱特征在特征识别方面的优势,目前高光谱图像处理技术已经被广泛应用到各种场景中[1-2]，例如精准农业[3]、海洋监测[4]以及城乡规划[5]等。在这些应用场景中，高光谱图像分类起到了重要作用。近年来，一些空谱联合分类算法被用来提升分类精度[6-8]。这些方法用于学习训练样本标签是可行的，然而在实际应用中并非如此。

有监督的高光谱图像分类算法要求样本是标记完成的，但是手动标记过程非常困难，仅凭视觉解释的训练样本并不可靠。具体来说，引入误标签的原因有如下几点：(1)全球定位系统会对目标对象的空间位置产生不准确的估计，导致很难确定高光谱像素的精确位置;(2)对于一些场景，比如海洋和湿地，这样的场景人类无法到达，在这种情况下，基于人类视觉解读的训练样本标签不可避免会产生噪声;(3)当标记一个包含许多不规则形状土地覆盖物的场景时，人工贴标签的过程中会产生错误。

为了解决训练样本的误标签问题，对计算机视觉领域进行了深入的研究。LU等人[9]提出一种基于曼哈顿距离优化的学习模型来检测弱噪声标签。FOODY等人[10]发现,噪声标签会影响基于支持向量机的机载制图分类。虽然许多研究已经解决了计算机视觉领域的噪声标签问题，但由于高光谱图像的高维和非线性结构，这些方法不能直接扩展到高光谱图像误标签分类中。最近几年，关于带有噪声标签的高光谱图像分类算法得到了关注。KANG等人[11]首次提出了基于光谱检测和边缘保持滤波的噪声标签检测和校正方法。TU等人[12]通过融合光谱角度和局部离群值因子来检测高光谱图像中的噪声标签，实验结果表明，该算法能有效地检测出有噪声的标签。密度峰值(density peak,DP)聚类算法作为一种鲁棒的聚类算法首次在科学杂志上被提出[13]。TU等人[14]首次利用DP聚类算法来检测高光谱图像训练样本中的误标签，基于DP聚类的高光谱图像误标签检测算法在检测过程中没有考虑相邻光谱像素之间的空间相关性。为了解决这一问题，TU等人[15]提出一种新的基于空间DP聚类(k-spatial density peak,K-SDP)的噪声标签检测算法，该算法通过加入中心样本的邻域样本来进一步检测中心样本的异常程度。然而，参考文献[14]和参考文献[15]中没有考虑原始高光谱图像中存在稀疏噪声的问题。参考文献[16]中提出一种基于核熵分量分析(kernel entropy component analysis,KECA)的噪声标签检测方法，但是，该算法在检测过程中没有考虑到训练样本的上下文信息。多种基于约束能量最小化(constrained energy minimum,CEM)算法已被广泛应用于高光谱图像处理中。ZOU等人[17]提出一种用于高光谱图像目标检测的二次约束能量最小化检测器。此外，ZHANG等人[18]提出一种混合稀疏性和CEM的检测器，以提高目标检测的性能。CEM也有效地应用到了高光谱图像误标签检测上。TU等人[19]提出了一种层次约束能量最小值(hierarchical constrained energy minimum,HCEM)方法来检测经过监督任务训练的原始训练集的错误标记样本，该方法可以准确地去除原始训练集的噪声标签，有效地提高监督分类任务的性能。但是，该算法的一个缺点是使用原始的光谱角制图算法(spectral angle mapping,SAM)来衡量光谱向量的相似度。原始的SAM是一种全局性的描述指标，当部分波段属性值有变化、或全部波段属性值具有不同的变化值时,往往导致光谱角余弦的失真。

为了解决参考文献[14]～参考文献[16]和参考文献[19]中所出现的问题，本文作者提出基于低秩稀疏和改进光谱角制图的密度峰值聚类算法(low rank sparse-normalized spectral angular mapping density peak clustering,LRS-NSAMDP)。相比于DP聚类算法[14]和K-SDP[15]算法，本算法的改进是去除原始高光谱图像中的稀疏噪声，提取高光谱图像中的低秩成分，降低每一类样本中的加权平均局部密度，从而减少了光谱向量中的误标签数目，提高了分类精度。相比于基于层次约束能量最小值的高光谱图像误标签分类算法[19]，本算法对原始的SAM算法进行改进，将光谱向量在波段上的属性值除以该光谱向量的模进行归一化，相比于SAM算法降低了同类像元之间的光谱角，使同类像元更加接近，从而更容易检测出训练样本中的像元之间差异较大的误标签。通过以上两个改进，相比于其它先进的遥感图像误标签分类算法，提升了总体精度(overall accuracy,OA)、平均精度(average accuracy,AA)和kappa系数。

1 相关技术

1.1 信号子空间估计

一幅原始高光谱图像Y≡[y1,y2,…,yQ]，Q代表每一波段的像素数。由于高光谱图像相邻波段之间的高相关性，根据线性回归理论和最小二乘法理论[20]，假设zi为传感器在第i波段读取的相关系数向量，所以有:

zi=Z∂iβi+ξi

(1)

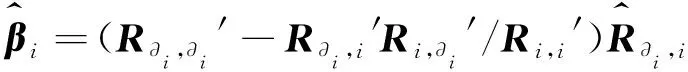
(2)

(3)

40年来，特别是党的十八以来，云南铁路抓住国家西部大开发和云南面向南亚东南亚辐射中心建设的机遇，积极争取国家政策支持，铁路投资、规划项目落地和开通运营里程保持高位增长。

1.2 光谱角制图

SAM是KRUSE等人在1993年提出的[22]，把图像中的每一个像元的光谱视为一个高维向量，通过计算两向量之间的夹角来度量光谱间的相似性，夹角越小，两光谱越相似，属于同类地物的可能性越大，因而可根据光谱角的大小来辨别未知数据的类别。分类时，通过计算未知数据与已知数据间的光谱角，并把未知数据的类别归为最小光谱角对应的类别中,如下式所示：

(4)

式中,L为波段数，A和B分别表示两个光谱向量在L个波段上的属性值，α为光谱角。夹角越小,余弦值较大；相反夹角大,相应的余弦值就较小。

2 基本低秩稀疏和改进SAM的新方法

图1是所提出的LRS-NSAMDP的流程图。主要分为5个步骤：(1)基于低秩稀疏表示的高光谱图像低秩特征提取；(2)计算各个类中训练样本间的距离；(3)训练样本局部密度的计算；(4)检测误标签训练样本；(5)支持向量机分类。

Fig.1 Flow chart of LRS-NSAMDP algorithm

2.1 基于低秩稀疏表示的高光谱图像低秩特征提取

(5)

式中,⊗表示克罗内克乘积，‖·‖表示矩阵的范数，I表示单位矩阵，Z表示相关系数矩阵，z为向量化Z，M为掩模，φ(z)表示正则化函数，δ是正则化系数，y为向量化图像Y。设掩模Mp作用在未观测到的像素p所对应的高光谱图像yp，所以有：

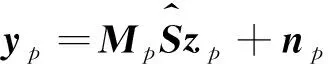
(6)

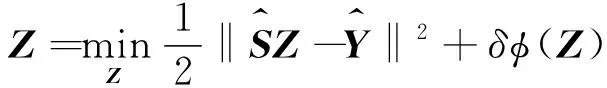
(7)

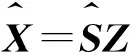
2.2 计算各类中训练样本间的距离

(8)

(9)

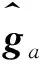
dl=[dl,l1,dl,l2,…,dl,lj]T

(10)

2.3 计算训练样本的局部密度

为了计算训练样本间的局部密度，定义截止距离dc，计算方式如下：

(11)

式中,S(t)为将Dj的上三角矩阵中的非零元素从最小到最大排序得到的矩阵，Nj为第j重样本总数,θ为随机参数，〈·〉为四舍五入运算。根据得到的dc矩阵计算每一类的局部密度ρ=∑exp[-(Dj/dc)2]。

2.4 检测误标签训练样本

根据每一类中每一个训练样本的局部密度，误样本可以通过线性阈值决策函数计算得到：

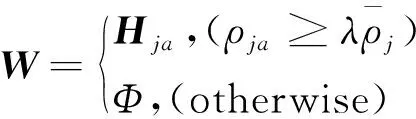
(12)

3 结果与分析

3.1 实验数据集

Kennedy Space Center(KSC)数据集是由AVIRIS高光谱仪于1996年在佛罗里达州肯尼迪太空中心采集的512像素×614像素大小的高光谱图像，包含224个波段，经过噪声去除后还剩下176个波段，空间分辨率是18m，有13个地物类别，总样本大小为5211。

University of Pavia(PaviaU)数据集是由ROSIS高光谱仪在帕维亚大学上空采集的610像素×340像素大小的高光谱图像，共包含9类地物115个波段，去掉含噪声波段后，其余103个波段作为实验数据集，总体样本大小为42776。本算法的实验以及对比算法实验的运行环境为12G内存，英特尔酷睿i5 2.2GHz的CPU，开发环境为MATLAB R2018a。图2和图3分别给出了两种数据集的假彩色图像、地物真值图和每一类物种。

Fig.2 KSC dataseta—false color image b—ground object truth map c—name of each species

Fig.3 PaviaU dataseta—false color image b—ground object truth map c—name of each species

3.2 实验参数分析

本算法提出的两个参数分别为：计算局部密度的随机参数θ和检测误标签训练样本的随机参数λ，图4和图5中分别展示了在KSC和PaviaU两个数据集上的不同参数下对OA的影响。为了证明算法的有效性，后续实验使用广泛应用在高光谱图像分类算法中的支持向量机(support vector machine,SVM)作为分类器，具体使用LIBSVM工具箱中的分类器，SVM的参数采用交叉验证的方式来确定。对于KSC数据集，对每一类随机选取25个真实样本和5个不确定标记样本，对于PaviaU数据集，对每一类随机选取50个真实样本和10个不确定标记样本。

Fig.4 On KSC dataset, the parameter θ and λ coefficient of different local densities λ impact on OA

Fig.5 On PaviaU dataset, the parameter θ and λ coefficient of different local densities λ impact on OA

根据图4和图5可以看出，随机参数θ在两个数据集上的波动范围相较于系数λ较小，比如在PaviaU数据集上，最大的局部密度只比最小的局部密度高2%左右，而在KSC数据集上最大的局部密度比最小的局部密度要高15%以上，因此决定本算法的精度值主要是随机参数θ。从图4和图5还可以看出,在KSC数据集上，当取θ=11、λ=0.2时,可以取得局部最优的OA值;PaviaU数据集上,当取θ=20、λ=0.2时，可以取得局部最优的OA值。因此对于一个新的数据集，建议取θ=20、λ=0.2作为提出算法的参数设置。

3.3 算法创新性实验验证

Table 1 Umber of false labels in each class detected by different detection algorithms under different uncertain samples

为了验证改进光谱角制图算法的优越性，在此将多种距离度量算法应用在本算法当中，比如，欧几里得距离(Euclidean distance,ED)[23]、光谱信息散度(spectral information divergence,SID)[24]、相关系数(correlation coefficient,CC)[25]以及SAM[22]。根据表2可以明显看出，本文中提出的归一化光谱角相似度算法取得了较优的分类精度，因此后续的对比实验采用本文中提出的归一化光谱角相似度算法来度量距离。

Table 2 Classification performance of KSC dataset under the false labeles detected by different distance measurement algorithms

3.4 不同的误标签检测算法性能比较

将本算法和先进的误标签检测算法进行对比，具体包括SVM算法[26]、DP聚类算法[14]、K-SDP算法[15]、KECA算法[16]和HCEM算法[19]。本算法的实验参数采用第3.2节中给出的参数，为了保持对比算法在最优的条件下进行对比，所有参数采用文献中给出的默认参数。在KSC数据集上，实验采用每一类25个正确样本加5个不确定样本、25个正确样本加15个不确定样本。在PaviaU数据集上，实验采用每一类50个正确样本加10个不确定样本、50个正确样本加20个不确定样本。限于篇幅，图6和图7中分别展示了在KSC数据集上25个正确样本加5个不确定样本和PaviaU数据集上50个正确样本加10个不确定样本下的不同误标签检测算法随机一次地物分类图。表3和表4中分别展示了不同误标签检测算法在KSC和PaviaU数据集上随机运行10次后求平均值的分类精度表格。

Fig.6 Feature classification map (25T+5U) obtained by different algorithms in KSC dataset

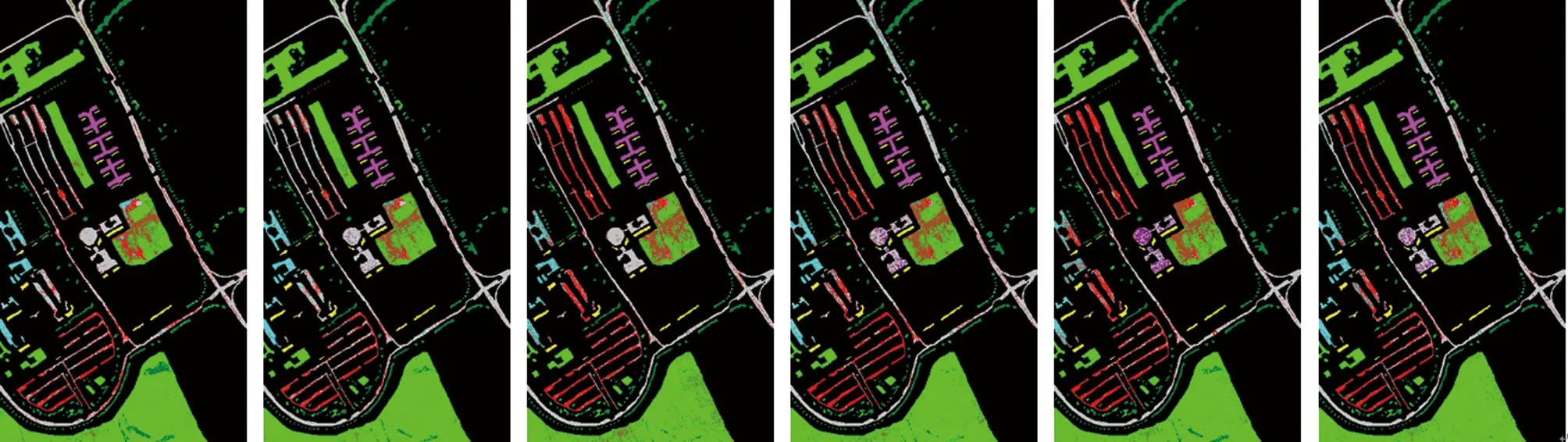
Fig.7 Feature classification map (50T+10U) obtained by different algorithms in PaviaU dataset

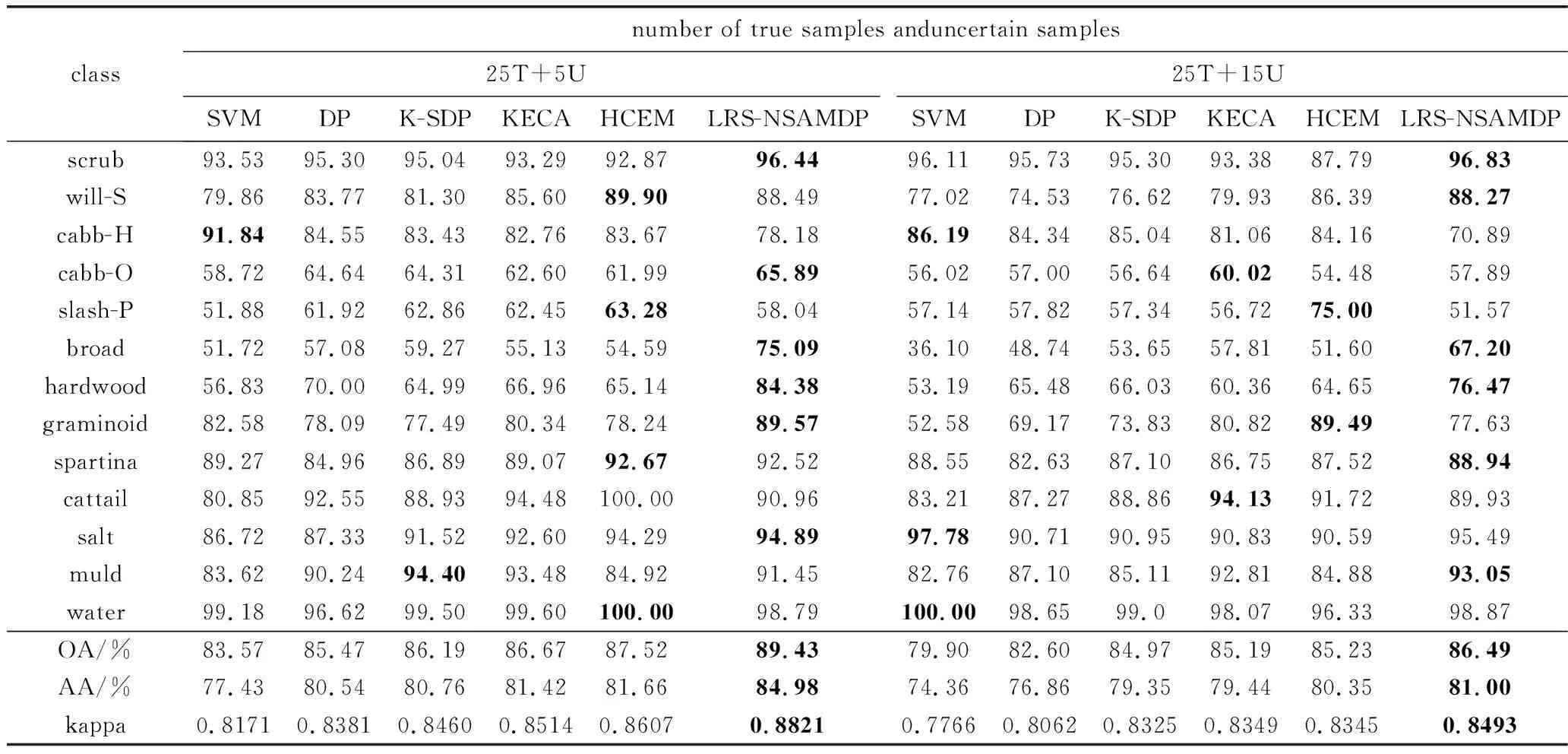
Table 3 Classification accuracy under different false label algorithms on KSC dataset

Table 4 Classification accuracy of PaviaU dataset with different false label algorithms

根据图6可知，本文中提出的LRS-NSAMDP算法和真实地物分类图更相似，证明了相比于SVM、DP、K-SDP、KECA和HCEM算法，本文中提出的算法可以有效地去除带有误标签的训练样本。由表3可以看出，当每一类训练样本中包含5个不确定样本时，本文中提出的算法的OA值要比SVM的OA值高5.86%，此外，和两个高光谱图像误标签检测算法DP聚类和K-SDP聚类相比，本算法对原始高光谱图像提取了低秩成分，提高了原始高光谱的质量。根据第3.3节可知，本算法相比于DP聚类和K-SDP聚类可以有效减少训练样本中的误标签，在KSC数据集上的不同误标签样本下，都提升了分类精度。相比于KECA算法，本算法使用改进的光谱角制图算法充分获取每一类训练样本间的上下文信息，在每一类包含5个不确定的训练样本上OA提升2.76%。相比于使用未改进光谱角制图的HCEM算法，本算法克服了原始光谱角余弦的失真问题，能够抑制误差，在每一类包含15个不确定的训练样本上OA提升1.26%。同时根据图7和表4可以得出同样的结论，例如，当每一类训练样本中包含10个不确定样本时，本算法相比于SVM、DP、K-SDP、KECA和HCEM算法，OA分别提高了6.76%,4.58%,3.94%,2.38%,1.24%，在两种数据集上充分证明了本算法的有效性。

图8中给出了不同训练集下使用不同误标签检测算法的总体精度柱状图。其中包括本算法和5种不同对比算法进行10次重复实验后获得的OA平均值。

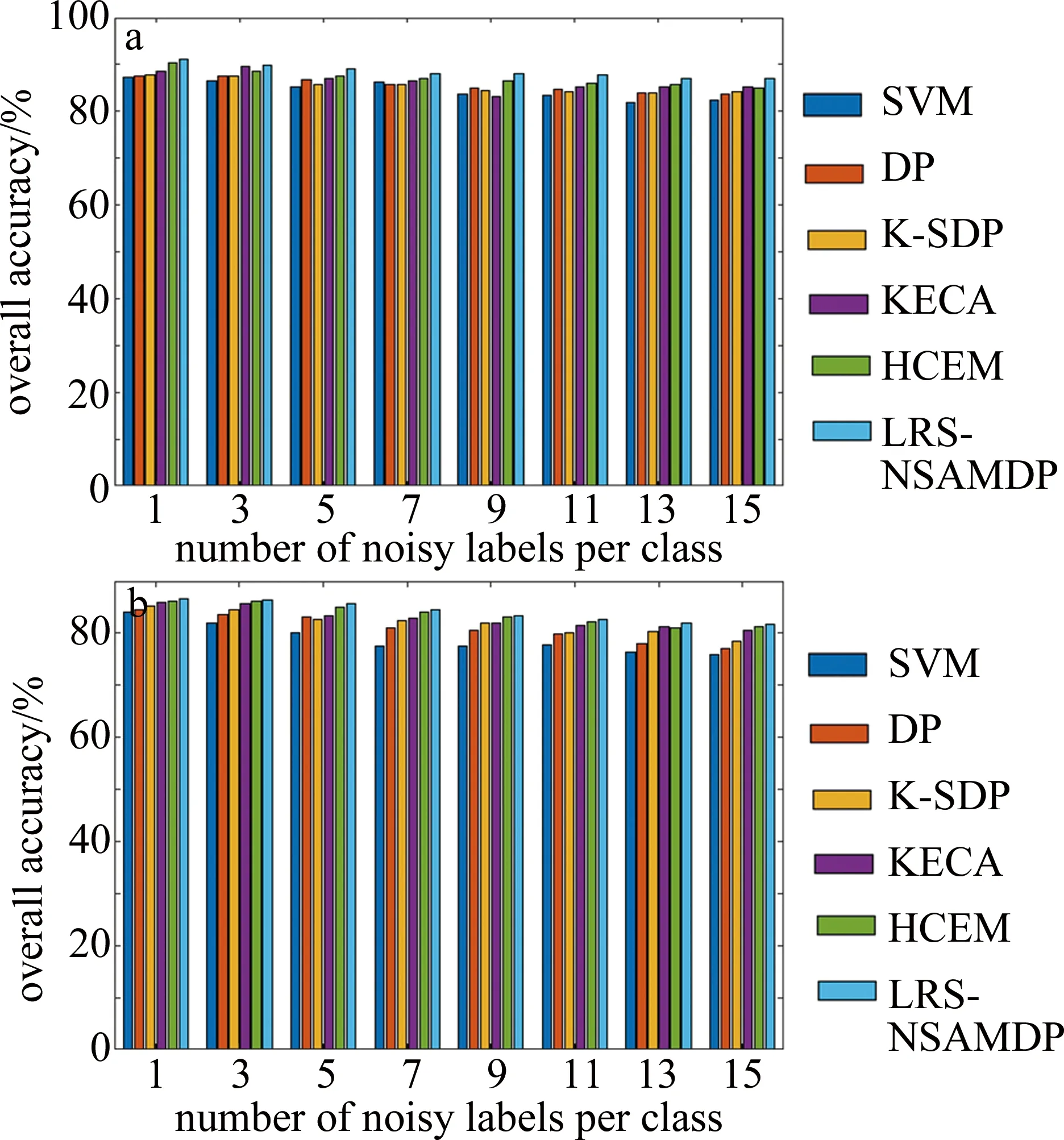
Fig.8 OA obtained by using different false label detection algorithms in different training sets

可以看出,本算法相比于SVM、DP、K-SDP、KECA和HCEM算法，两个数据集上都提高了OA值，证明了在误标签的检测过程中，提出的算法相比于对比算法更具有鲁棒性。

3.5 提出的误标签检测算法的误差分析

表5中给出本方法在两个数据集上所有检测失败的不确定样本数，检测失败的不确定样本造成检测算法的误差。其中,6×13表示在训练样本中所有的不确定样本数目，6表示每一类中的不确定样本数目，13表示类的数目(实验数据重复5次求得平均值),其它类推。首先明显看出，本算法所有检测失败的不确定样本相比于DP算法和K-SDP算法检测失败的不确定样本数目少，证明本算法检测性能优越。仍然会出现检测误差的原因主要还是算法本身造成的。(12)式采用简单的线性阈值决策函数，该函数可能会导致无法准确度量、检测、去除临界值附近的待检测样本，造成系统误差。此外，本算法采用改进SAM算法来衡量光谱相似度和利用光谱信息，在检测过程中并没有利用到遥感图像的空间信息,这也会造成系统误差,可以采取自适应调节的软阈值决策函数、联合样本之间的空间上下文信息等来减少系统误差。另一方面，测量仪器、设备装置和环境会导致随机误差,可以通过增加求平均值的次数以及使用最小二乘法求得最优值来减少随机误差。但是随机误差仍是不可以避免的。

Table 5 Detection performance of false labels for the proposed method on two datasets

4 结 论