基于光纤传感的形状传感发展研究
刘紫娟,李永倩*,张立欣,范海军
(1.华北电力大学 电子与通信工程系,保定 071003;2.华北电力大学 河北省电力物联网技术重点实验室,保定 071003;3.华北电力大学 保定市光纤传感与光通信技术重点实验室,保定 071003)
引 言
光纤形状传感是最近热门的一种新兴传感技术,其通过多路光纤在同一形变下的不同应变响应,来测量和确定光纤本身或者与之紧密接触的物体位置和形状[1]。近年来,光纤形状传感技术在众多领域中得到了广泛的研究和关注,如医疗领域中的探针、软体操作器、内窥镜等;航空航天领域中关键结构体的变形监测,如飞机蒙皮、机翼等的形变监测;桥梁在线变形测量;柔性机器人触手形状感测等。
形状传感技术由传统的弯曲测量发展进化而来,传统的形状传感器以电信号测量为主,包括电阻率和应变传感器、光电传感器、微电子机械传感器等[2],这些传感器虽成本低廉,但其布线复杂性高,受电磁干扰影响严重,且高度依赖供电设备,具有诸多的局限性。光纤传感技术因其抗干扰能力强、测量距离长、传输可靠性和精度高、布线简单等优点[3-5],为形状传感技术提供了一个十分有前途的方向。
本文中综述了光纤传感技术在国内外多个领域的研究进展,阐述并分析光纤形状传感技术的基本原理和关键技术的发展情况,总结目前光纤传感技术所面临的主要问题,最后提出对解决相关问题和未来发展方向的看法。
1 光纤形状传感基本原理
目前对光纤形状传感器的设计和测量方法的研究可以分为两大类:一类是基于光纤布喇格光栅(fiber Bragg grating,FBG)的形状传感器;一类是基于分布式光纤传感(distributed fiber optic sensing,DFOS)的形状传感器。
1.1 基于FBG的形状传感
以光纤为传输介质的FBG传感技术,是通过观察光纤传输过程中FBG中心波长的漂移量,来感知外界温度或应变等待测参数的变化[6]。由模式耦合理论得到FBG中心波长λB,可用下式表示[7]:
λB=2neffΛ
(1)
式中,neff为有效折射率,Λ为FBG的光栅周期。因为neff和Λ都是温度和应变的函数,当FBG工作的环境温度和所受应变发生改变时,neff(T,ε)和Λ(T,ε)就会发生变化,相应地,FBG的中心波长就会发生漂移,其中心波长漂移量可用下式表示[8-9]:
ΔλB=2ΔneffΛ+2neffΔΛ=
λB[(1-Pe)ε+(α+ξ)ΔT]
(2)
式中,Pe为FBG的有效弹光系数,ε为FBG所受到的应变,α为光纤的热膨胀系数,ξ为光纤的热光系数,ΔT为温度变化量。假设外界温度恒定,即ΔT=0,则可以忽略温度对λB的影响,(2)式就可以简化为:
ΔλB=λB(1-Pe)ε
(3)
已有的研究表明,光纤所受应变和其曲率之间是成线性关系的[10-12],从(3)式可以看出,通过测量FBG形状传感器中心波长的漂移量,就可以计算得到传感器所受的应变量,从而得到FBG传感器所在光纤段的曲率信息。
光纤在感受到弯曲形变后,光纤上刻写的FBG会因为应力产生相应地中心波长漂移,基于FBG的形状传感将光纤中FBG产生的波长漂移量相应的转换为该位置的曲率,再将光纤按空间分辨率量级分成若干段,计算出每个光纤段的曲率,通过一定的还原算法就可以在电脑端还原整条光纤的形状。
1.2 基于DFOS的形状传感
由于光纤介质的不均匀性,光在光纤中传输会产生散射信号[13-14],分布式形状传感器通过将光纤中产生的散射信号和本地参考信号做对比处理,从而得到光在光纤中传输产生的参数变化量,来确定光纤所受到的应变,并通过数据处理,对应变进行定位。以采用多芯光纤(multi-core fiber,MCF)[15-16]为传输介质的形状传感器为例,则分布式形状传感器的简化理论模型如图1所示[17]。图中,R为光纤的弯曲半径,L是传感器的初始长度,d为纤芯和传感器中性轴的距离,ΔL为纤芯被拉伸/压缩的长度。

图1 分布式形状传感器简化理论模型
设L1和L2侧所受应力为ε1和ε2,则两侧应力变化量应有如下关系式:

(4)
以基于布里渊散射信号的系统为例,其布里渊频移(Brillouin frequency shift,BFS)受温度和应变两种变量的影响,其中温度系数为CT,应变系数为Cε,则其变化量可以表示为[18]:
ΔνB=CTΔT+CεΔε
(5)
假设多芯光纤在同一位置上所受温度相同,则选用多芯光纤中任意两个芯的布里渊频移量相减,就可以消除温度对BFS的影响,得到下式:
ΔνB,2-ΔνB,1=
CTΔT2+CεΔε2-(CTΔT1+CεΔε1)=
CT(ΔT2-ΔT1)+Cε(Δε2-Δε1)=

(6)
式中,Cκ=Cεd,为光纤的曲率系数,κ=1/R,为光纤的曲率。
1.3 空间重构算法
空间曲线其实可以看作是同个空间下的任意一个粒子或无数个粒子的运动轨迹进行组合的结果,弗莱纳(Frenet-Serret)公式是对3维空间中连续可微曲线上粒子运动的描述,即对空间曲线的切向、法向、副法向方向之间关系的表示[19]:
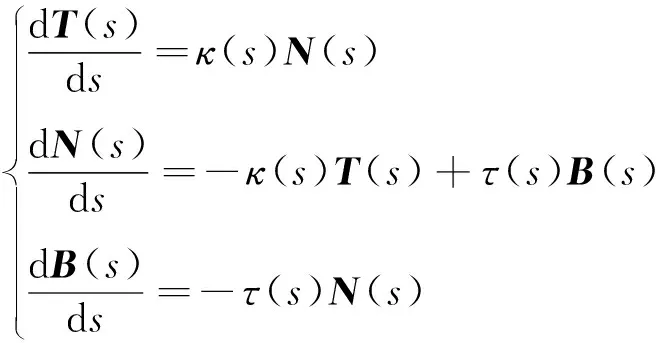
(7)
式中,s代表空间中曲线的长度,T(s)为单位切向量且指向粒子运动的方向,N(s)为单位法向量,B(s)为单位副法向量,κ(s)为曲线曲率,τ(s)为曲线挠率。
光纤形状传感的还原重构就是将整条光纤看作若干个光纤段,这些光纤段在空间中就是若干个空间曲线,将这些空间曲线结合各种空间坐标算法拼接在一起,就可形成一条完整的有形态的光纤。在基于弗莱纲框架的基础上,出现了很多空间坐标算法,如多项式拟合[20]、三次样条插值算法[21]、曲率差值算法[22]等。
2 关键技术研究现状
1996年末~2000年初,分布式弯曲测量的方法开始出现并流行,与此同时,各类复用技术的出现与成熟进一步推动了光纤形状传感技术的研究[23]。1996年,光纤光栅的波分复用(wavelength division multiplexing,WDM)技术首次应用于结构弯曲传感和振动模式分析中,通过对检测到的光纤光栅中各个波长的漂移量进行解调,得到光纤所受的应变,以此实现对桥梁弯曲形变的监测[24]。1999年,BALAKRISHNAN等人完成了一种新型2维弯曲感应带的开发,商业上称为ShapeTape,通过检测压力感应带的不同区域获得相应数据,并通过算法处理在计算机上显示ShapeTape的弯曲轮廓,如图2所示[25]。

图2 ShapeTape的重建弯曲轮廓[25]
2000年后,以形状感应为主题的专利和文章开始大量涌现,虽然ShapeTape在应用中基本消失,但在多芯光纤中使用FBG的波长变化进行高精度和高灵敏度的曲率传感一度成为了当时热门的研究方向[26-27]。2004年,MILLER等人利用准分布式测量进行了形状传感的研究,基于密切圆理论,将光纤分段近似为一段段圆弧,进行了2维形状重构,完成了空间分辨率40cm、总长度15m的FBG测量[28]。同年,上海大学的QIAN等人在FBG曲率传感的基础上,搭建了基于FBG的渐进式内窥镜形状感知系统,通过模拟仿真和实验,实现了内窥镜的形状还原[29]。
受光纤光栅数量和空间分辨率的限制,分布式光纤形状传感逐渐出现在人们的视野中。2006年,美国LUNA公司的DUNCAN等人采用光频域反射(optical frequency domain reflectometry,OFDR),以长度为1.1m、刻写了FBG的多芯光纤为传输介质,实现了2维及3维形状传感,且其空间分辨率达到了1cm[30]。2007年,该公司结合瑞利后向散射的相关理论,提出基于瑞利散射的光纤形状传感技术[31]。2010年,该公司的FROGGATT等人又申请了以螺旋多芯光纤为传输介质的形状传感器,并利用OFDR系统进行导管空间位置定位的专利,通过测量纤芯中的瑞利散射来确定应变量,实现了长度1.2m、误差2.24mm的多芯光纤的形状传感[32]。后来LUNA公司将该专利转让给美国直觉外科公司(Intuitive Surgical),将其运用到微创介入导航系统Ion中[33],实现了医学领域的应用。图3为集成了光纤形状传感器后的Ion系统进入肺部神经末梢的过程。
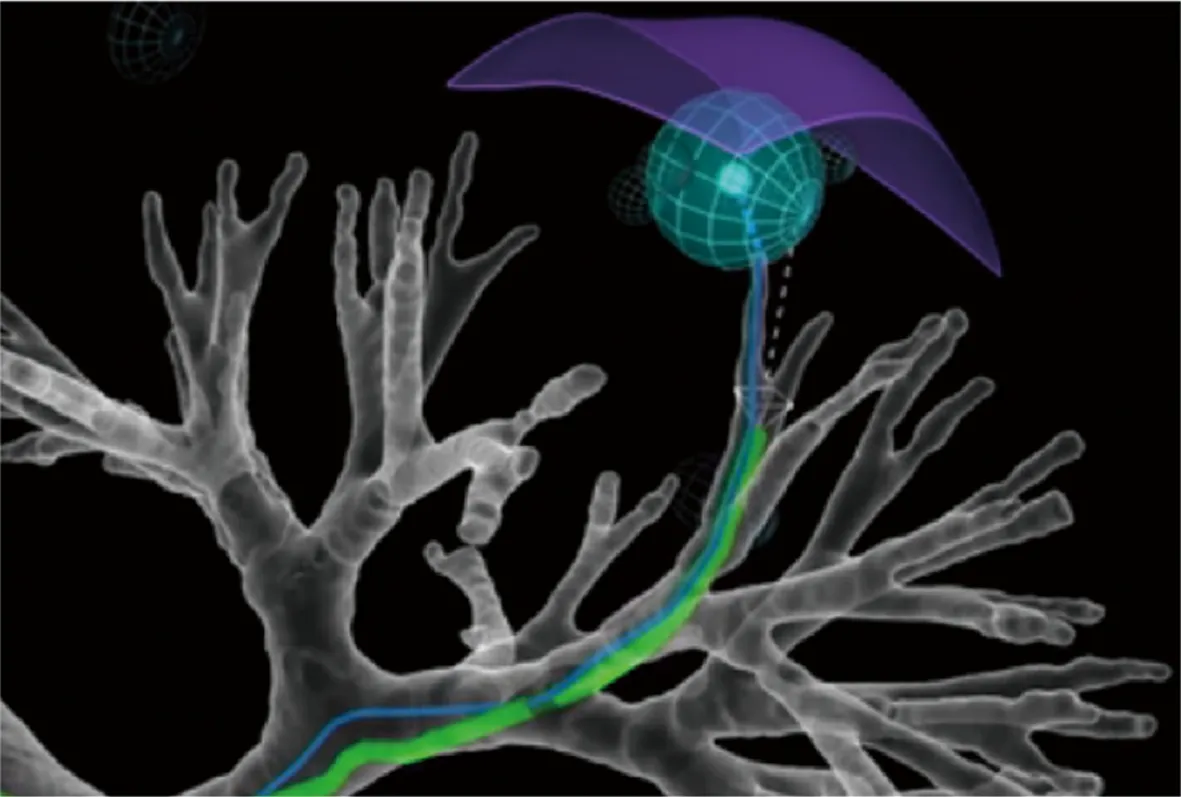
图3 集成了光纤形状传感器后的Ion系统进入肺部神经末梢的过程[33]
2011年,上海大学的ZHU等人提出一种基于空间正交曲率信息的3维曲线重建方法,实验中结合了FBG传感器,运用到太空机械臂、柔性杆结构等结构的变形监测中[34]。2012年,美国国家航空航天局MOORE等人通过数值求解Frenet-Serret 公式,利用OFDR系统获得的离散应变值,进行了三芯光纤的3维形状还原,最大误差值为7.2%[35]。同年,LUNA公司将长为30m的MCF形状传感器以两种不用的方式敷设在长为10m的柔性结构的表面,布设方式分别为U型和回旋型,并通过数据处理得到了柔性材料的表面形状[36]。图4为柔性结构空间形变测量装置和结果。图4a为真实实验中光纤的敷设,图4b为在电脑软件上还原的光纤形状。可以看出,该实验及算法较完美地实现了短距离的形状传感。

图4 柔性结构空间形变测量装置和结果[36]
2014年,上海大学的SHEN等人利用FBG作为传感元件,利用不同的固定曲率对形状传感器进行了标定,得到FBG波长漂移量与曲率的关系,对细长柔性基杆形变曲率进行实时监测,并使用离散曲率拟合方法重构了曲线形状。图5为柔性基材曲线重构结果[37]。
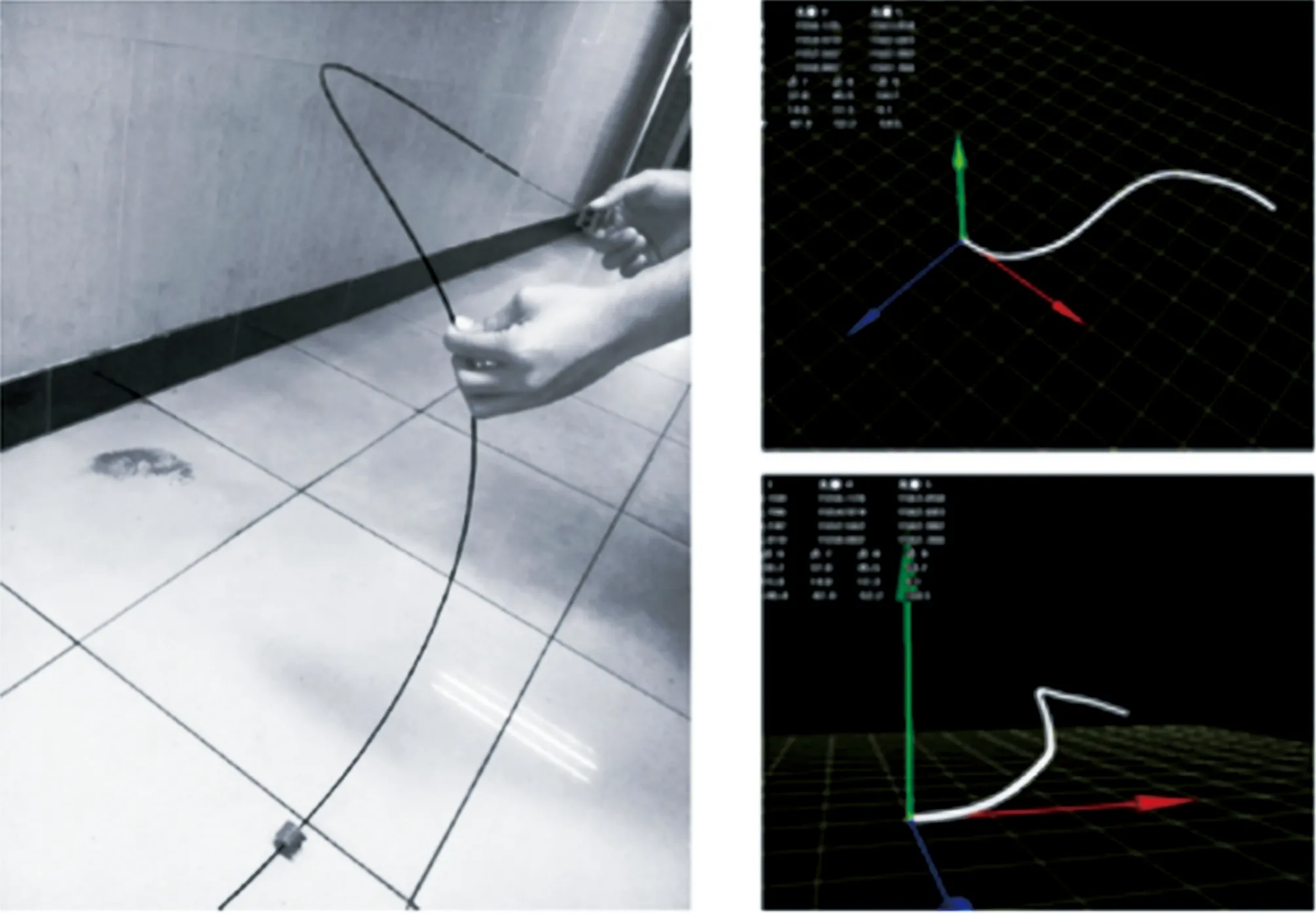
图5 柔性基材曲线重构结果[37]
2015年,上海交通大学的WANG提出了一种基于FBG的软体机械臂3维形状传感网络及方法,该方法将检测到的FBG传感网络中的应变量转换成节点的空间位置,通过仿真证明了其对复杂3维形状有较高检测精度[38]。2016年,华中科技大学ZHAO课题组在国内首次验证了MCF中外芯的布里渊频移和光纤曲率之间存在线性关系,并搭建了基于七芯MCF的分布式布里渊光时域分析(Brillouin optical time domain analysis,BOTDA)系统,所用光纤长度为1km,实现了20cm空间分辨率的曲率测量,其系统原理框图如图6所示[39]。

图6 基于七芯MCF的分布式BOTDA系统原理框图[39]
此次实验利用较为成熟的双端BOTDA系统,增加了七芯光纤的扇入扇出装置,实现了简单的MCF形状测量。通过单独测量每个纤芯的布里渊增益谱,可以获得MCF不同方向的应变量,整合就可以得到MCF精准的形状。美中不足的是,此次实验仅仅测量了两个外芯的布里渊增益谱,未实现多芯的同时测量,也未展开形状重构工作,但使用光纤分布式测量系统极大地增加了传感距离,也为解决多芯形状传感器测量距离短板问题提供了一个极具前景的方向。在这之后,哈尔滨工业大学的DONG课题组设计了基于差分脉冲对(differential pulse pair,DPP)BOTDA系统的高性能温度不敏感形状传感器,实现了10cm的空间分辨率[40]。2019年,瑞士学者SZOSTKIEWICZ等人提出了一种基于七芯光纤和相敏光时域反射计(phase sensitive optical time domain reflectometry,φ-OTDR)的高灵敏度分布式形状传感器,经实验验证其可以实现长24m的MCF上低至0.3με的高应变灵敏度,空间分辨率可达10cm[41]。
值得一提的是,分布式形状传感是在分布式光纤传感技术基础上的进一步探索和应用,在这一领域中,华北电力大学LI课题组对布里渊分布式传感技术开展了持续深入的研究,在利用BOTDR、φ-OTDR、单端BOTDA等传感系统对应变、温度等参数进行高空间分辨率、高精度、实时测量研究中,积累了较多的经验,有助于后续进行更深入的形状传感研究。
使用多芯光纤制作形状传感器的一个重要问题就是在测量和缠绕的过程中会不可避免地发生扭曲,如何消除扭曲所带来的测量误差,进而提高形状测量和重构精度,成为近年来众多学者研究的热点。2020年,英国南安普顿大学的ZAFEIROPOULOU等人提出了一种基于布里渊光时域反射(Brillouin optical time domain reflectance,BOTDR)的分布式曲率传感器[42]。该传感器首次使用了特殊设计的七芯D形光纤,其目的是在实际应用中将D形光纤的平面作为参考面,在缠绕和敷设时始终使光纤平面保持在同一方向,最大程度地避免MCF产生扭曲。实验中通过比较中心芯和3个外芯间的相对布里渊频移,测量了59mm~227mm直径线轴的曲率,误差在9%~15%之间,其七芯D形光纤结构如图7所示。
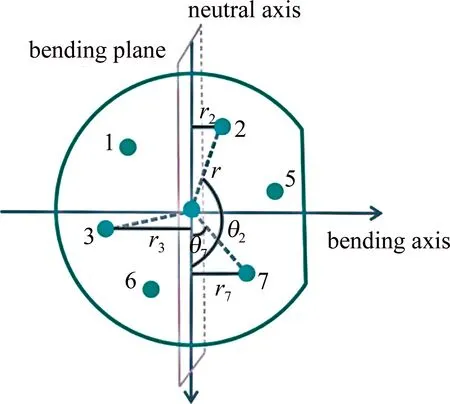
图7 七芯D形光纤剖面结构[42]
2020年,北京信息科技大学的ZHU等人针对微创手术中软体操作器工作时的形状测量,提出了一种螺旋型布设光纤光栅的形状传感方法[43]。采用无粘结剂的形式将光纤光栅植入柔性硅胶片中固定,实验灵敏度为65.822pm/m-1,空间分辨率为3cm,测量误差在2.9%左右[8]。2021年,KHAN等人提出并比较了两种带有FBG的多芯形状传感器结构,测量了MCF的曲率和扭转,两种结构一种带有直芯,另一种带有螺旋芯,结构如图8所示。光纤放置在已知配置中比较它们的测量精度,对比发现,扭曲测量实验中直芯和螺旋两种光纤的平均误差分别是146.50°/m和26.57°/m,并且螺旋芯光纤的扭转测量误差非常低[44]。同年,LU等人提出一种基于MCF的FBG形状传感算法,该算法使用MCF中刻栅的结构进行迭代曲率和扭转估计,降低了信号噪声及环境扰动对形状测量和位置估计的影响,该算法使形状测量和尖端定位的准确度有了显著的提升。除此之外,为了消除空间域的纵向感应曲率和扭转中的短峰,引入一种优化的局部移动平均算法,进一步地提高了测量精度和传感布设长度[45]。

图8 a—带有FBG的直芯传感器结构[44] b—螺旋芯传感器结构[44]
3 结束语
光纤形状传感器通过检测FBG中心波长的漂移量或者分布式光纤传感系统的频移量,来获得光纤在传输过程中因弯曲形变产生的应变量,将整条光纤看作若干条空间光纤曲线,通过公式计算就可以获得不同光纤段的曲率信息,结合以Frenet-Serret公式为架构的各种空间坐标算法,就可以还原出光纤的形状。光纤形状传感技术相较于传统的电学形状传感技术,具有布线简单、灵敏度高、不受电磁干扰等特点,并且可以适用于多个领域的多种场景中。光纤形状传感器中,基于FBG的形状传感器在探索前期就得到了广泛的关注,其精度较高,数据处理较为简单,但受光纤光栅数量的限制,只适合较短距离的测量。基于MCF的分布式光纤形状传感器已被证明可以达到远距离形状测量的目标,从而展示了分布式光纤传感系统在形状传感上的远大应用前景。
目前形状传感技术得到了许多学者的探索和研究,但是仍有许多关键问题没有得到解决。
(1)使用MCF作为长距离传输介质,其系统成本高昂且实现的难度和后期数据处理的复杂度都将大幅增加,如何降低成本及实现难度,并开发出性能更加优越的处理方法,是需要思考和前进的方向。
(2)对复杂度高和需要精准姿态的目标进行测量时,对形状传感系统空间分辨率的要求就极大地提高了,在保证测量精度的同时还需要实现非常高的空间分辨率,避免光在传输中的干扰耦合,这是需要克服的困难。
(3)在实际应用中MCF的扭转会对测量结果造成较大的影响,目前有学者提出螺旋多芯光纤的解决方案,但是螺旋多芯光纤的制作成本高且制作技术不成熟,暂时无法大规模应用,探索新的传输介质和解决办法也是急需解决的问题。除此之外,数据处理算法、测量技术等软技术方向也有待突破,是非常值得广大学者进行深入研究的方向。

