基于MIMO的无人机斜程激光通信性能分析

唐翰玲，李勇军，李 怡，赵尚弘

（空军工程大学 信息与导航学院，陕西 西安 710077）

引言

随着无人机性能的提高，新一代的军用或民用无人机在军事侦察、反恐维稳、海洋利益维护等方面都得到了广泛的应用。无人机光通信作为一种低成本、宽带宽、高速率的新型通信技术已经成为一种最有潜力和发展前景的通信方式[1-4]。尤其是在难以架设基站的战场环境下，其抗干扰、组网方便快捷的特点更是体现出巨大的技术优势。

无人机工作于大气环境中，受大气湍流的影响，信号光到达接收端时产生光强起伏、到达角起伏等现象，同时光链路信道还受大气衰减以及平台本身振动带来的联合影响[5]，使光链路信道恶化，严重影响通信质量。研究表明多输入多输出（multiple input multiple output,MIMO）技术可以有效用来对抗信道的衰落，改善和提高系统的性能[6]。文献[7-8]研究了发射分集和接收分集等增益组合的无线光通信系统在Gamma-Gamma 分布大气湍流信道中的误码率(bit error rate,BER)性能，研究了水平链路下光MIMO 技术克服大气湍流带来的系统性能改善，但忽视了无人机振动带来的指向误差的影响，尤其是对于光MIMO 技术改善无人机平台大气湍流和指向误差影响下的空地斜程信道[9-10]误码率性能的研究鲜有报道。本文以典型无人机“彩虹-6”无人机参数为基础，根据无人机光通信平台载荷和空间受限，振动大的突出特点，综合分析了大气湍流和指向误差联合影响下单输入多输出(SIMO)下行斜程链路和多输入单输出(MISO)上行斜程链路误码率性能。

1 理论分析模型

1.1 系统信道模型

基于光MIMO 技术的激光通信系统如图1所示[11]。

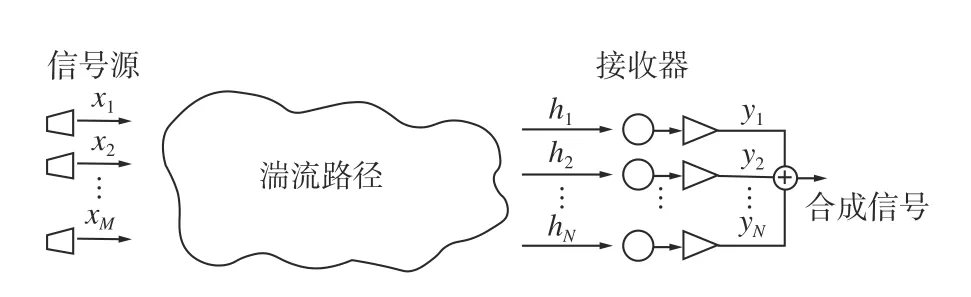
图1 光MIMO 系统示意图Fig.1 Schematic diagram of optical MIMO system

假设采用强度调制/直接检测（intensity modulation/direct detection,IM/DD）的二进制的开关键控（on-off keying ,OOK）调制方式，第n个接收窗口输出的信号可以写为[12]

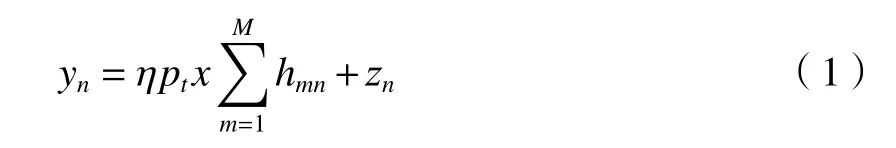
式中：x∈{0，1}是无人机等概发射的比特信号；η是光电转换系数；pt是接收的平均功率；hmn=hlhpha为信道的随机衰减因子；hl为大气信道确定性的路径损耗，为了便于分析，假设其值为1；hp和ha分别为相互独立的指向误差和大气湍流引起的衰减；zn是均值为零，方差的加性高斯白噪声。

为了避免发射和接收窗口相互之间的干扰，确保信道之间的独立性，发射端或接收端窗口之间至少间隔一个相关长度的距离。受无人机载荷和空间的影响，难以在无人机平台上布设多个接收和发射窗口，但地面受此限制小。因此，为了克服大气湍流带来的不利影响并根据无人机振动大、载荷和空间都受限的突出特点，本文下行链路采用SIMO光链路系统和大气湍流、指向误差相结合的信道衰减模型，上行链路采用MISO 光链路系统和大气湍流信道衰减模型对系统误码率进行分析。

下行链路采用合并信号复杂但接收信号利用率高的最大比合并(maximum ratio combining,MRC)[11]；对于上行链路为MISO 系统，只有一个接收器，不涉及信号的合并。对接收总功率进行归一化处理后可以得出上行和下行总信号分别为[12]

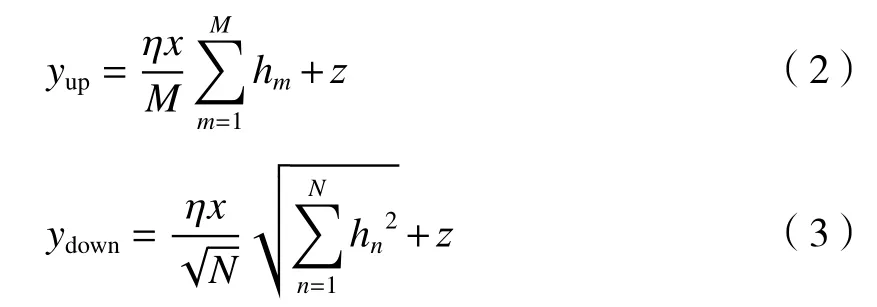
式中：参数M、N是为了使发射总功率和接收窗口的面积与单输入单输出(SISO)情况下相等，由此我们可以得出上、下行链路的信噪比公式分别为

1.2 大气湍流

经实验验证，Gamma-Gamma 分布能较全面准确地描述各种强度湍流，因此本文的光通信链路采用Gamma-Gamma 分布来进行分析。Gamma-Gamma 模型下衰减系数ha的PDF（probability distribution function）为[13]

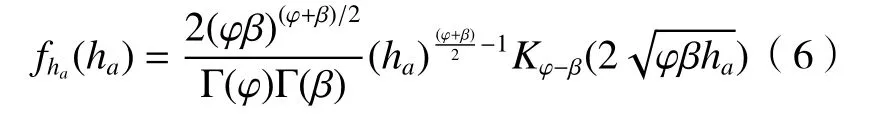
式中：Γ(*)为 Gamma 函数；Kφ-β(*)为第二类贝赛尔函数；φ、β分别表示小尺度和大尺度湍流引起的光强起伏参数；φ、β和大气条件有关，在平面波情况下分别表示为[14]

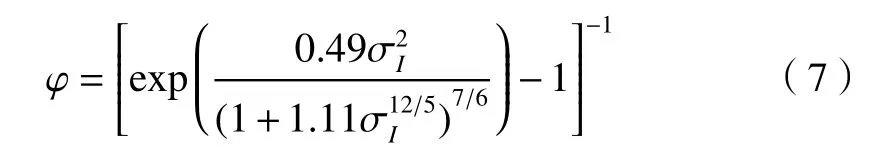
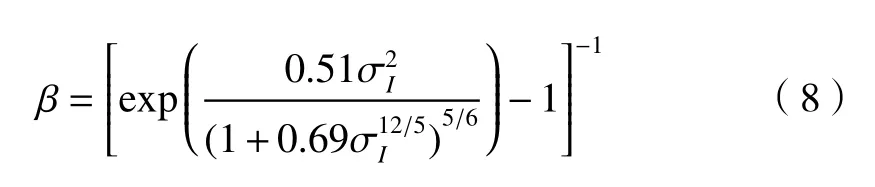
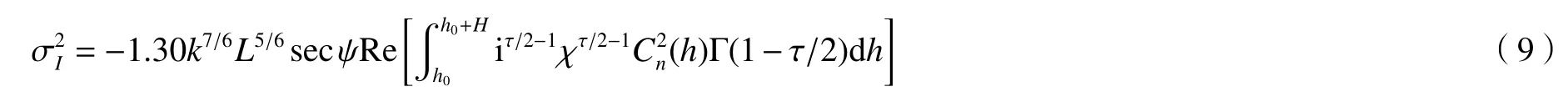
式中：L是激光传输距离；ψ是天顶角；H是机载平台的飞行高度；h0是地面接收器的海拔高度，本文中假设其值为0；k=2π/λ是波数；χ=1-(h-h0)/(H-h0)是归一化距离变量；为大气折射率结构常数，可由Hufnagel-Valley 模型来描述，可以表示成[16]：

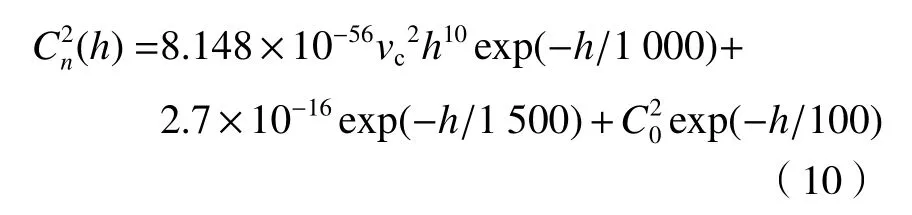
式中：vc为 垂直路径风速；为近地面大气折射率结构常数。（9）式中的τ 是关于随海拔高度h的幂率谱指数函数，通常可以表示为[10]

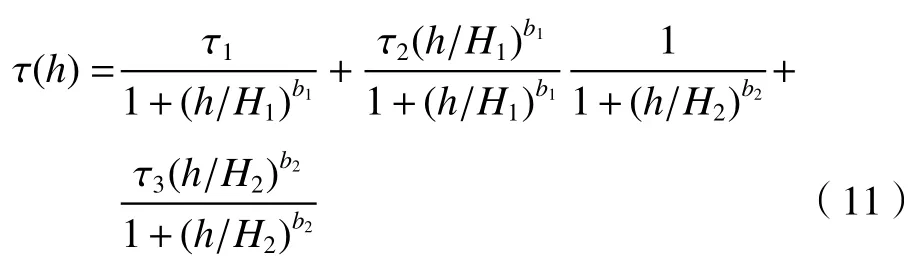
式中：τ1=11/3、τ2=10/3及 τ3=5分别表示三层高度谱模型中对应的边界层、对流层和平流层的幂率谱指数；H1=2 000 m、H2=8 000 m为垂直方向分层界限；b1=8、b2=10为数值系数。

1.3 指向误差

指向误差也是影响激光链路性能的重要因素之一，无人机相对于卫星和地面平台振动明显，是无人机指向误差的主要影响因子，因此本文忽略视轴误差，假设每个接收器是面积为S的圆形探测孔径，那么对于高斯光束，可以得出距离L处指向误差引起的衰减hp的分布函数为[17-18]

1.4 误码率

系统采用OOK 强度调制直接检测时，误码率可表示为[19]

1.4.1 下行链路

由系统模型知h=hpha，那么由（6）式和（12）式知指向误差和大气湍流联合下的链路衰减系数的概率分布函数为

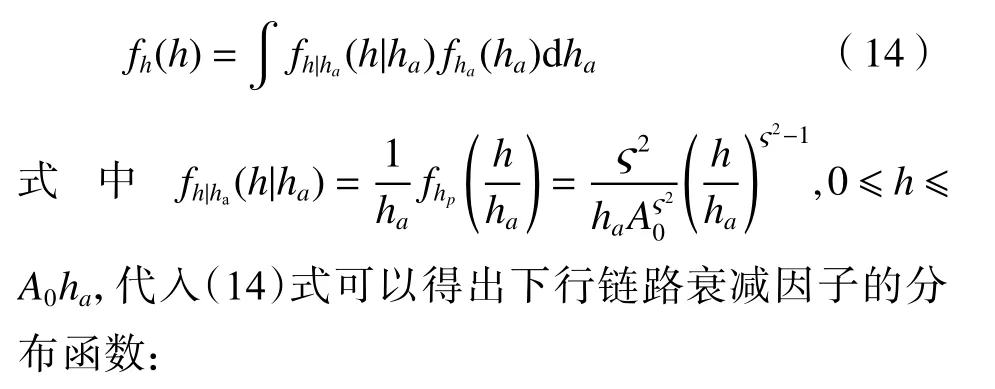
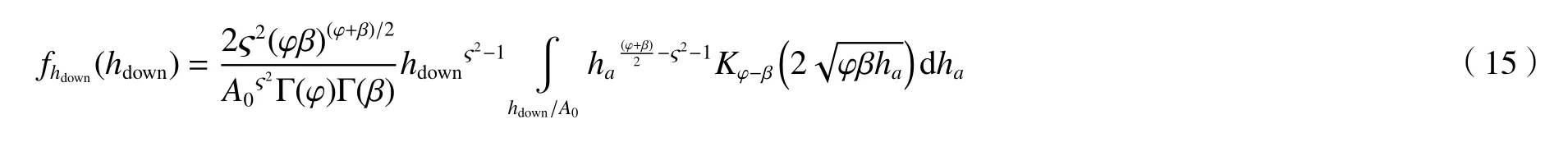
由Meijer 函数性质及（13）式可以将下行链路误码率表示为

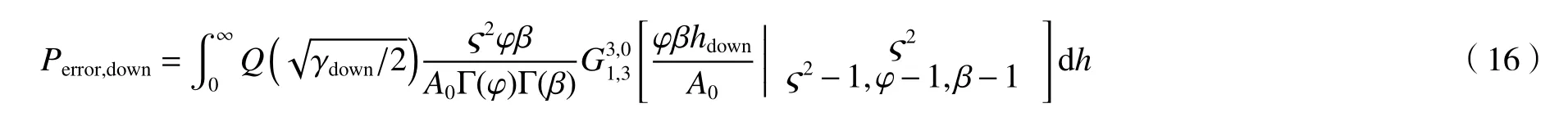
由文献[20]知：

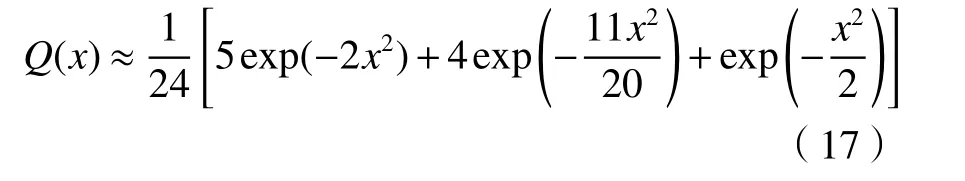
1.4.2 上行链路

由前文知，上行链路为MISO 系统，因此不涉及信号的合并问题，不考虑指向误差的情况下，其衰减因子的分布函数为

2 仿真及数值分析

典型高空无人机的巡航高度约为10 km，利用（18）式和（22）式分别对下行/上行链路误码率进行仿真计算，基本参数如表1所示：

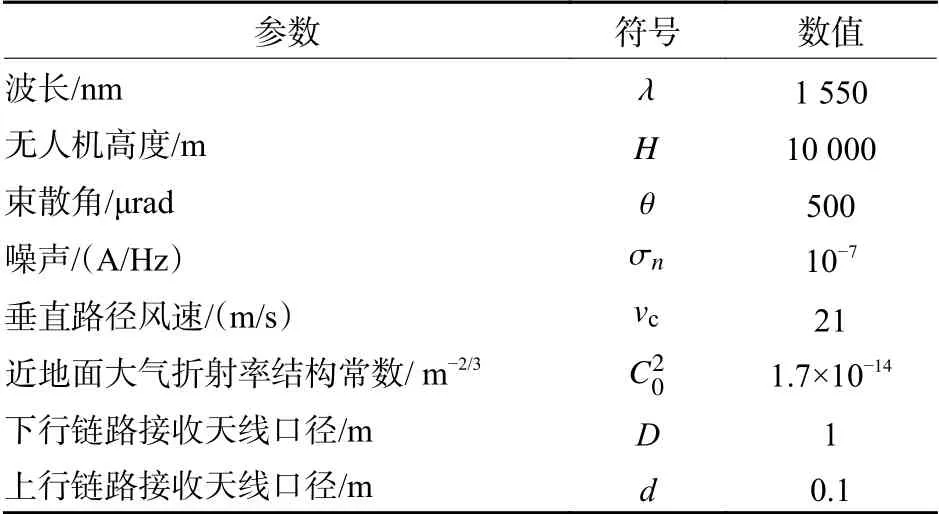
表1 仿真参数Table 1 Simulation parameters

2.1 下行链路

在下行链路光SIMO 系统中，随着接收窗口数N的增加，系统误码率随平均信噪比的变化如图2所示。

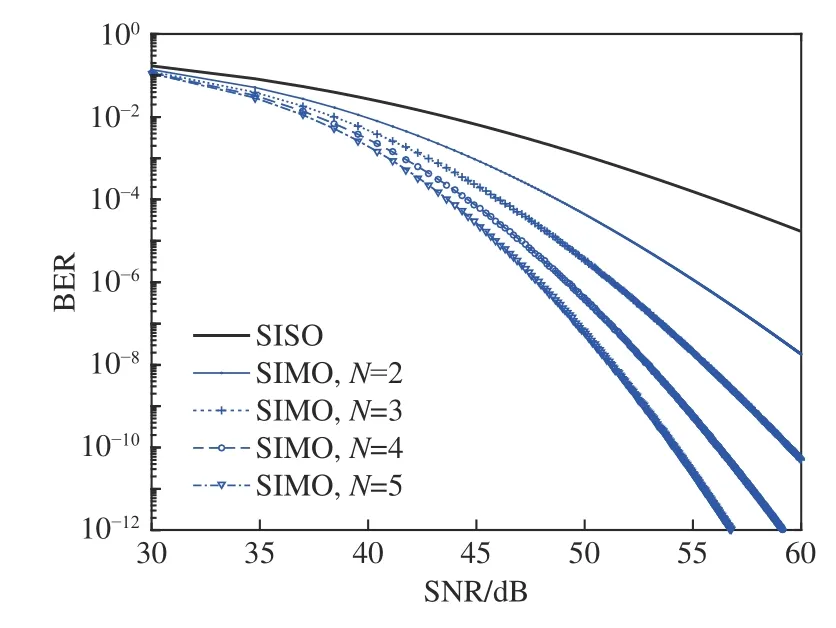
图2 下行链路SIMO 系统误码率随平均信噪比变化曲线Fig.2 Variation curves of bit error rate of downlink SIMO system with average signal-to-noise ratio

从图2 中可以看出，随着信噪比的增加，系统误码率减小；随着接收器个数N增加，达到相同误码率所需要的信噪比减小，系统误码率性能得到改善。并且随着系统误码率要求的提高，SIMO 技术相对于SISO（单输入单输出）技术对系统信噪比的增益越加明显，这一特点可以使无人机降低发射功率，节省更多的能量增加留空作业时间。随着N的增加，系统性能改善的效果减弱。设系统误码率要求为10-6，当接收器个数N从1 增加到2 时，达到系统误码率要求的所需信噪比减小了大约10 dB。当接收器个数N从4 增加到5 时，达到系统误码率要求的所需信噪比只减小了大约1.3 dB。工程实践中综合考虑性能及成本因素，接收器个数可以设计成3 个以达到优化系统性能的目的。

图3 展示了下行链路系统误码率随天顶角变化的规律曲线。从图3 中可以看出，一方面近地面大气折射率结构常数增加时，系统的误码率增大；另一方面，随着天顶角的增大，系统误码率增加。并且SIMO 技术相对于SISO 技术对误码率性能的改善效果迅速减小。以为例，天顶角等于10°时，误码率性能从10-5提高到10-8；天顶角等于30°时，系统的误码率误码率性能从10-4提高到10-6左右。这是因为天顶角增大，一方面使激光通信链路长度增加；另一方面使大气湍流对通信链路的影响加剧。

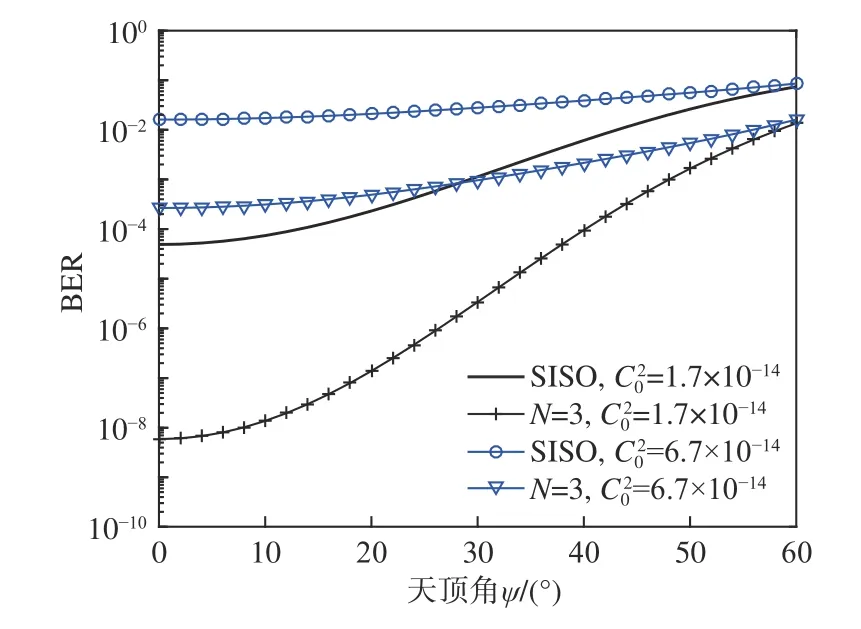
图3 下行链路系统误码率随天顶角变化曲线（SNR=50 dB）Fig.3 Variation curves of bit error rate of downlink system with zenith angles （SNR=50 dB）

图4 为光强闪烁指数随天顶角变化曲线。当天顶角较小时，光强闪烁指数变化较为缓慢。超过30°以后，光强闪烁指数随天顶角变化急剧增大，导致大气湍流的影响增强，信道恶化。从图3 和图4 可以看出，大气湍流对“空-地”激光通信系统性能非常明显。因此为了保证通信质量，“空-地”斜程通信的天顶角控制在30°的小范围内较好，且天顶角越小，大气湍流对信道的影响越小，通信质量越好。

图4 光强闪烁指数随天顶角变化曲线Fig.4 Variation curve of light intensity scintillation index with zenith angles

图5 显示了不同指向误差与接收器口径比值条件下下行链路误码率随束散角的变化情况。同一束散角条件下，的值越小，误码率性能越好；当比值小于1 时，随着束散角的增大，误码率性能逐渐变差，最后趋于稳定；当比值大于1 时，误码率先减小后增大，最后趋于稳定。由于无人机平台振动明显，当巡航高度为10 km 时，比值通常大于1。因此工程实际中可以根据使用环境，选取一个束散角的最优值使误码率性能最佳。

图5 下行链路系统误码率随束散角变化曲线Fig.5 Variation curves of bit error rate of downlink system with beam divergence angles

2.2 上行链路

上行链路由于地面站的稳定性好，因此高度10 km 的光通信指向误差的影响比较小。本文仅对上行链路MISO 系统误码率性能进行分析，如图6所示。

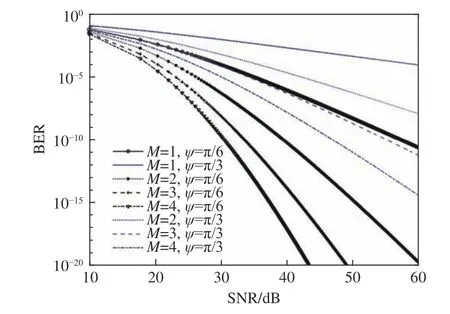
图6 上行链路MISO 系统误码率随平均信噪比变化曲线Fig.6 Variation curves of bit error rate of uplink MISO system with average signal-to-noise ratio

在上行链路光MISO 系统中，天顶角增大时，系统误码率明显增加。以M等于3 为例，达到系统误码率10-6指标要求的信噪比从25 dB 增加到约38 dB。原因同下行链路一致，天顶角的增大，使斜程光链路距离增大，大气湍流效应加剧，使信道环境变差，通信质量降低。随着发射器的增加，信噪比增益增大，达到系统指定要求所需信噪比大大减小。以天顶角为30 度为例，M从1 增加到2 时，所需信噪比从39.5 dB 减小到29 dB，减小了约10.5 dB。同时，随着发射器M的增加，增益效果降低。当M从3 增加到4 时，所需信噪比只减小了约1.5 dB。因此在工程实践中，发射器个数为3 时就可以得到一个理想的信噪比增益，使效益最大化。

3 结论

基于典型无人机的性能参数，针对无人机振动大、载荷受限的特点，理论分析了“空-地”斜程环境下适用于无人机平台的光SIMO/MISO 技术对系统误码率性能的影响。仿真分析表明：1）相对于SISO 的光链路传输，采用SIMO/MISO 技术的单天线无人机平台，既可以降低功率、减小体积，同时也能有效改善大气湍流带来的不利影响，提高通信质量。通过仿真分析，当下行链路接收天线为3 和上行链路发射天线为3 时就可以得到一个理想的信噪比增益，使效益最大化；2）天顶角对斜程链路的光强闪烁指数影响较大，为了保证通信质量，天顶角应控制在30°小范围内；3）由于机载平台振动明显，指向误差对误码率影响明显，尤其是当指向误差与接收天线口径比值大于1 时，存在一个最优束散角使误码率性能最佳。本研究为无人机机载光通信的优化使用提供了参考。下一步将进一步引入高效编码来优化无人机光链路的性能，并搭建实验平台对实验结论做进一步的验证。