基于赋权连接图的增量式运动恢复结构算法

江 滔，马 泳，黄 珺，王贺松，樊 凡

（武汉大学电子信息学院，湖北武汉430072）

引言

近年来，运动恢复结构算法(structure from motion，SfM)在文物数字化[1]、虚拟现实技术[2]、3D 游戏[3]、地理测量[4]等方面发挥了重要作用。根据图像迭代计算方式，SfM 可以分为增量式和全局式两种[5]。全局式SfM 以全局的方式同时获取所有相机的相对运动，能够避免场景漂移问题，但精度较差且难以修正出现的错误[6]。增量式SfM则是通过图像逐个配准的方式来完成整体的重建，对错误匹配有很强的容错能力，总体精度较高，引起了广泛和深入的研究，其基本流程见图1。

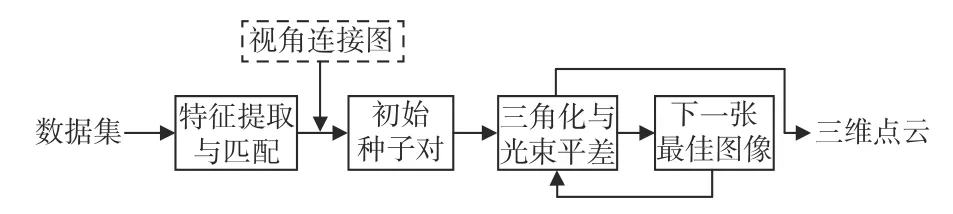
图1 增量式SfM 基本流程示意图Fig.1 Pipeline of incremental SfM

如图1所示，增量式SfM 首先通过图像特征提取与匹配[7-10]建立一个以图像为顶点、图像对的匹配关系为边的无向图，称为视角连接图或连接图[5]，继而在连接图中确定一组匹配关系鲁棒的初始种子对，这样就能通过三角化与光束平差[11-12]构建一个初始的三维点云结构。然后再不断地搜索下一张最佳图像进行三角化与光束平差，从而进一步丰富和完整场景目标的三维结构。不难看出，初始种子对和下一张最佳图像的选择对增量式SfM 至关重要，它们分别决定了三维结构的初始化以及增量式SfM 的重建顺序，也是本文研究的主要内容。

首先，在确定初始种子对时，由于增量式重建对初始化过程的误差或者错误非常敏感[13-14]，要求初始种子对的选择必须高精度且高效。在提高精确度方面，Haner 等人[15]提出一种基于协方差传播的种子对选择算法，通过最小化相机协方差传播率和重投影误差来选择种子对；Cui[16]等人选择了拥有待校准相机数目最多且最符合相机旋转先验的图像对作为种子对。这些算法通过为每个图像计算额外信息的方式寻找最优的初始种子对，精度高，但复杂度也高。在提高效率方面，Colmap[17]和VSFM[18]选择了排除纯旋转关系且具有足够多特征匹配对数量的图像对作为初始种子对，效率上有了较大提升，但是忽略了在视角连接图中种子对与相邻顶点之间的关系，鲁棒性差。

其次，在搜索下一张最佳图像时，不佳的选择不仅会污染已恢复的三维结构，还可能导致连续性的图像配准错误，从而导致重建效果下降甚至重建失败。为此，研究者提出了大量的下一张最佳图像的搜索方法。Degol 等人[19]通过预先在目标场景中添加自定义的标志物，选择与已重建结构相比标志物最多的图像作为下一张最佳图像，该方法要求将标志物置于场景目标表面，通用性大大受限；Cao 等人[20]在视角连接图中找到与已重建结构存在最多匹配关系的图像，作为下一张最佳图像；Colmap[17]在Cao[20]等人的算法基础上，进一步考虑了图像与已重建结构的特征点分布的均匀程度，图像特征点分布越均匀越有利于相机内外参的求解。但是针对连接图中顶点度数的不同情况，上述算法没有采取下一张最佳图像选择的区别化优先级策略，且需要在视角连接图上全局搜索下一张最佳图像，算法复杂度较大。

针对上述问题，本文提出一种基于赋权连接图的增量式运动恢复结构算法，首先定义了基于图像间立体匹配质量的连接图权重因子，具有定量评价双视图立体匹配质量和指导初始种子对选择的优势。在此基础上提出了基于度数感知的初始种子对选择算法，从而达到赋予高度数的顶点更高选择优先级的目的。最后提出了基于候选集的下一张图像评分算法来搜索下一张最佳图像，通过对搜索范围的约束，提升了算法的效率。

1 基于赋权连接图的增量式重建算法

本文提出的基于赋权连接图的运动恢复算法的核心部分包括：1）定义图像立体匹配质量，创建赋权视角连接图；2）在赋权连接图中边的权重的基础上，搜索度数感知的最佳初始种子对；3）根据赋权视角连接图中已重建顶点的连通性，创建下一张最佳图像候选集，并提出基于顶点度数与特征点分布的图像评价函数，对候选集中所有图像评分，选择评分最高的作为下一张最佳图像。每次新得到下一张最佳图像后，通过三角化和光束平差增量式地丰富三维结构，图2 是本文的算法框图。本节将重点介绍上述3 个核心部分。

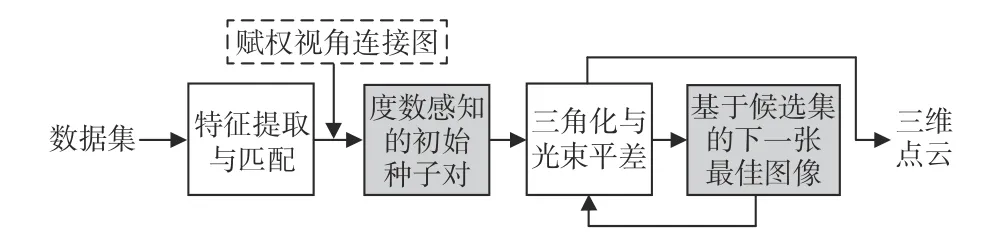
图2 基于赋权连接图的增量式重建算法流程图Fig.2 Pipeline of weighted scene graph based incremental SfM

1.1 赋权连接图的创建

增量式SfM 算法第1 步是通过图像两两之间的特征点提取与匹配，将所有满足图像匹配关系[21]的图像对加入匹配集M，进而根据匹配集M中的图像匹配关系对来构建视角连接图[22]，图3(a)是视角连接图的示意图。

图3 视角连接图与赋权视角连接图示意图Fig.3 Schematic of scene graph and weighted scene graph

传统视角连接图通过边来单纯地反映图像之间存在的匹配关系，但是却没有反映该图像对作为初始种子以恢复初始三维结构的优劣。从一对图像间恢复出三维信息的任务又称双目立体视觉，双目立体匹配关系由两方面因素决定[23-24]：1）匹配特征点数量，匹配的特征点数量越多，越有利于计算鲁棒的图像变换关系，从而进行三维重建；2）相机主光轴之间的相对旋转角度，相对旋转角度过小，目标场景立体现象不明显，不利于三维结构的恢复；相对旋转角度过大，图像对重叠面积较小，从而导致存在特征点误匹配的数量增多，立体匹配的误差增大[24]。因此，为了衡量顶点间立体匹配关系的质量，本文定义了一种基于匹配特征点数量与相对旋转角度的权重因子w，并以此构建赋权连接图。图3(b)给出了赋权连接图的示意图，记赋权连接图G=(V,E,W)，其中顶点集代表输入图像集，边集代表图像匹配对，表示边集E中边元素的权重，基于匹配的特征点数量和相对旋转角度的赋权连接图权重因子wij定义为

式中：wNij表示顶点vi和vj间特 征点数量权重因子；wθi j表示顶点vi和vj对应图像间相对旋转角度权重因子；Ni j表示顶点vi和vj间 匹配的特征点数量；θij表示相对旋转角度；α 和 β分别是特征点数量权重因子和相对旋转角度因子的归一化系数，由于图像对存在足够的匹配特征点数量是完成图像匹配的基础，图像相对旋转角度是在该基础上成立的，因此本文设置归一化系数α和β的取值范围为0 ≤β ≤0.5 ≤α ≤1。当数据集拍摄的图像密度大或者图像质量较高时，由于提取的特征点数量大，可以适当减小 α并 增大 β；若数据集图像密度低或者图像质量低不利于特征提取与匹配时，则应适当增大 α并减小 β。

特征点数量权重因子wNij由特征点数量决定，定义其归一化的计算公式为

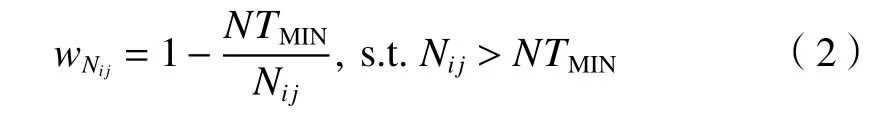
式中：NTMIN为图像对 (vi,vj)之间存在匹配关系的最低特征点对数目，当数据集的图像空间密度大或者图像质量高时，由于可以从图像中提取到大量的特征点，因此应提高NTMIN过滤掉匹配特征点数量少的图像对；反之，当图像空间密度低或者图像质量低时，应适当减小NTMIN使得匹配特征点数量较少的图像对也能参与到增量式重建。给定NTMIN的条件时，特征点匹配对Nij的数量越大，wNij越大，且。

相对旋转角度权重因子wθij由相对旋转角度θij与 最佳旋转角度 θBEST决定，定义其归一化的计算公式为

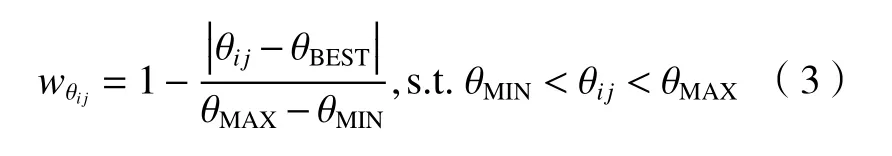
式中 θMIN和 θMAX分别为相对旋转角度的最小值和最大值，θMIN<θBEST<θMAX，因此wθij∈(0,1)。在实际中 θBEST一 般用中间值 (θMIN+θMAX)/2来近似。

本文创建的赋权连接图中的权重因子表征了图像对之间的立体匹配质量，权重因子越高，越有利于鲁棒地恢复相机位姿和特征点三维空间位置，也越有利于构建一个初始的三维结构。

1.2 度数感知的初始种子对选择

在完成权重因子计算并创建视角连接图后，下一步是在连接图中寻找初始种子对。一方面，从赋权连接图中边的角度，通过边的权重因子可以找出立体匹配质量好的图像对；另一方面，从赋权连接图整体的角度，由于度数大的顶点与其存在鲁棒的立体匹配关系的顶点更多，在对应位置上能进行更多次的三角化与光束平差计算，从而获得更完整和准确的三维结构，因此在其他条件如权重因子相似的情况下，应当给予度数大的顶点对更高的选择优先级。图4 给出了度数不同的初始种子对的重建结果，图4(a)和图4(b)分别是在同一赋权视角连接图中，权重因子相等但是度数不一样的初始种子对选择方式，在图中使用虚线框出；图4(c)和图4(d)分别是上述低度数和高度数初始种子对对应的重建结果，重建的目标场景细节使用红色椭圆框出。从重建结果可知，相对于低度数的初始种子对，度数高的初始种子对能获得结构更稳定、空洞更少、细节更丰富的三维结构。

图4 不同度数的初始种子对的重建结果Fig.4 Reconstruction results of initial seed pairs with different degree

因此，本文在赋权连接图权重因子的基础上，设计了一种度数感知的初始种子对优先级评价方法，记赋权连接图中图像对作为初始种子对的优先级Pi j为

式中Dij是图像对的归一化度数因子，定义为

其中di和dj分别为顶点vi和vj的度数，满足di,dj≥1，因此顶点对的度数和di+dj越大，Dij越接近1，否则越接近0。度数因子Dij与 权重因子wij之和越大，其作为初始种子对的优先级Pij越大，根据(4)式找到优先级最高的顶点对作为初始种子对。

1.3 基于候选集的下一张最佳图像搜索

初始种子对在经过三角化创建初始三维结构之后，剩余的图像就按照最有利于三维结构恢复的顺序，依次通过与该三维结构中已有特征点的匹配关系，来恢复该图像的位姿，并不断将计算得到的新的特征点三维坐标加入到现有三维结构中去。在这一过程中，下一张最佳图像的搜索是最重要的任务。该任务存在着效率和精度两个方面的要求，分别对应了下一张最佳图像的搜索范围和评价方法。

在下一张最佳图像的搜索范围方面，针对现有算法下一张最佳图像是在所有未配准图像的全局环境下进行，存在着搜索范围大、搜索复杂度高的问题，本文选择在已重建的顶点集附近搜索下一张最佳图像，通过限定搜索范围的方式提升重建效率。如图5所示，本文根据与已重建顶点的相邻关系，构建了下一张图像的候选顶点集：

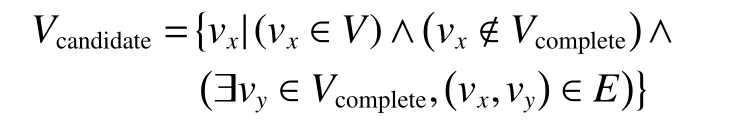
式中：Vcandidate代 表候选顶点集；Vcomplete代表已重建顶点集；V和E分别是赋权连接图G的顶点集与边集，所有与Vcomplete中的顶点相邻的顶点的组成了下一张最佳图像的候选顶点集Vcandidate，在图5 中橙色顶点代表下一张最佳图像的候选顶点，绿色顶点代表已重建顶点。

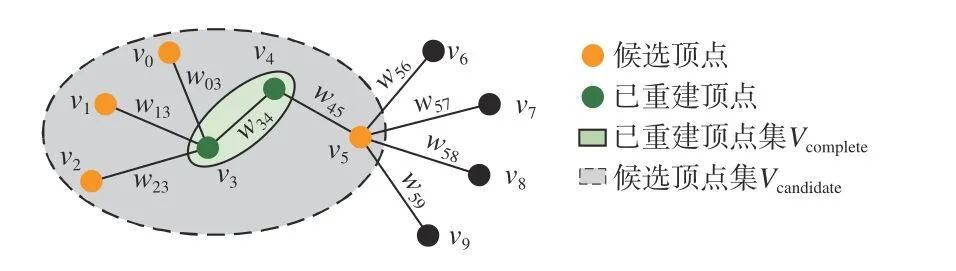
图5 下一张最佳图像候选顶点集示意图Fig.5 Schematic diagram of the next best image candidate set

在下一张最佳图像的评价方法方面，在对候选顶点作为下一张最佳图像的进行评价时，本文在考虑已恢复三维结构在候选图像上匹配特征点分布情况的同时，还考虑了候选顶点的度数对于下一轮迭代计算的影响。顶点度数高时不仅表明该顶点附近的视角信息丰富，而且在增量式迭代过程中，能有更多的顶点加入下一轮候选顶点集，为下一张最佳图像提供了更大的评价与选择空间。以图5 为例，若度数大的v5作为下一张最佳图像，那么下一轮迭代中，v6、v7、v8和v9都将加入候选顶点集，达到丰富候选顶点的目的。因此，对于候选顶点集Vcandidate中 的顶点vx，本文设计了一种基于顶点度数和特征点分布均匀程度的下一张配准图像评分函数Svx：

(6)式中f(vx)是的顶点vx的度数评价项，用于考察顶点vx对 于候选顶点平均度数相对大小，f(vx)定义如(7)式：

（7）式中dvx表示顶点vx在赋权连接图G中的度数，记候选集中顶点的数量为N，则候选集顶点的平均度数可以表示为

(6)式中g(vx)是图像特征点分布均匀程度评价项，为了评价已恢复结构在图像上匹配特征点的分布均匀程度，本文首先将图像按照不同的尺度划分成均匀的网格，然后统计每个尺度下存在特征点的网格的数量，最后再对不同尺度下的统计结果乘以不同的尺度系数，以此来衡量特征点在图像中分布的均匀程度。g(vx)定义如（9）式：

式中：L表示对图像进行划分的尺度数量，在尺度为l时，将图像均匀划分为 2l×2l的 网格；Kl表示图像在尺度l下的尺度系数，用于反映该尺度对于图像特征点分布均匀程序评价项的贡献，本文的尺度系数定义为Kl=2l；Ml表示图像在尺度为l时特征点的存在矩阵，其维度与网格被划分的维度一致，因此它是一个 2l阶 的方阵，若l尺度下图像的某一个网格内存在已恢复结构与当前图像匹配对中的特征点，那么方阵对应位置值为1，否则为0。因此尺度为l时存在特征点的网格数量可以通过Ml的L1范数‖Ml‖1表示：

表1 给出了图5所示的赋权连接图下，下一张最佳图像的评分过程。图5 中 (v3,v4)是初始种子对，此时候选顶点集Vcandidate={v0,v1,v2,v5}，如表1所示，给定尺度数量L=3时各个顶点的度数，给定视图3D-2D 匹配对中图像特征点的分布情况，根据(6)式计算出了不同的顶点作为下一张最佳图像的评分。

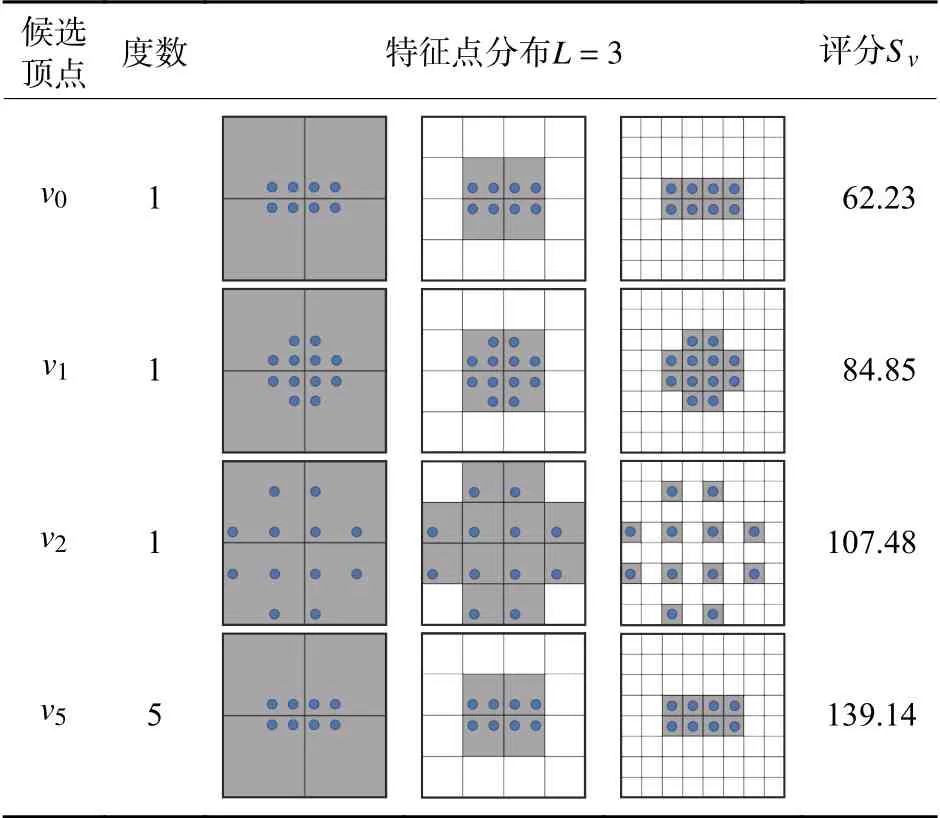
表1 候选集中顶点作为下一张最佳图像的评分Table 1 Score of candidate image as next best image

由表1 可知，在v0和v1度数相等的情况下，特征点数量多的顶点v1的 评分更高；在v1和v2顶点度数和特征点数量相等的情况下，在图形中特征点分布得更均匀的顶点v2的评分更高；在v0和v5特征点数量及分布相等的情况下，度数大的顶点v5评分更高。综上所述，在给定匹配特征点分布时，图5所示的连接图中评分最高的顶点v5将成为下一张最佳图像。

2 实验结果与分析

为了验证本文算法的在重建效果和算法复杂度上的先进性，选取了目前先进的3 个增量式重建算法VSFM[18]、Colmap[17]、openMVG[25]与本文算法进行对比实验。实验数据集来自Farenzena[26]和Olsson[27]，实 验 环 境 为AMD Ryzen 9 5900X 12 核CPU、INVIDIAGTX1060 6 GB 的GPU以及16 GB 内存的台式电脑。本算法关键参数的取值如表2所示。

表2 本文算法的关键参数设置Table 2 Key parameter settings of proposed algorithm

针对不同的增量式重建算法，三维重建算法的性能通过主观和客观两个方面进行评价，主观上通过观察重建效果来评价，包括重建的目标场景的完整程度、离群点的分布情况以及是否发生了场景漂移，即由于相机位姿恢复出现错误或者误差积累而导致重建目标偏移实际情况的现象[10]；客观上则可以通过相机校准率、重建耗时、点云数量以及点云生成速率等几个方面来进行评价，其中相机校准率指三维重建算法恢复出相机位姿的数目与数据中图像数量的比值，该值越高表明算法对不同视角的立体信息利用率更高，抵御噪声的能力越强，重建的结构更完整；重建耗时指增量式SfM 完成对所有图像的匹配并生成最终三维结构的时长，该值越小说明完成重建得更快；点云数量指最终的三维结构中的点云个数，该值越大表明结构三维信息越丰富；点云生成速率即点云数量与重建耗时的比值，反映了单位时间内算法恢复出的三维空间坐标数量，用于反映各个算法的效率；

表3 给出了不同算法在公开数据集上重建效果的表现。当数据集规模较小且目标特征点丰富时，如在Lund Cathedral 数据集上，4 种算法从整体来看都能对目标的重建取得较好的效果，由于本文算法更加强调下一张最佳图像在赋权视角连接图中的相邻性，仅存在于相邻图像之间的匹配特征点能够得到优先计算与重建，因此相较于其他算法，本文算法能够还原出更多的细节，如建筑物的顶部的轮廓更加鲜明、表中所示的建筑物表面镂空处重建得更加完整。在Gustav II Adolf 数据集上，由于目标表面光滑以及图像中背景天空部分较大等原因，图像的特征点数量较少，此时不同算法的重建质量出现了较大的差别，VSFM 和open-MVG 重建结果中都出现了较多的离群点，其中VSFM的重建结果中雕塑的头部已无法辨认，Colmap 和本文算法由于考虑了匹配特征点在图像上分布的均匀性，能够较好地选择出增量式重建过程中的下一张最佳图像，从而维持三维结构的鲁棒性；在Navona Square 和Piazza Erbe 数据集上，随着图像数量逐渐增多，VSFM 和Colmap 在重建过程中由于误差的不断积累造成了场景漂移，失去了对目标进行完整三维重建的能力，而openMVG 和本文提出的基于赋权连接图的增量式重建算法，都保持了较好的重建效果。如表3所示，在对Navona Square 和Piazza Erbe 数据集重建时，在一些目标有较大的角度变化的关键结构处，本文算法能够得到更多点云从而获得更加丰富的细节，这是由于本文对度数更高的顶点在下一张最佳图像候选集中赋予了更高的优先级，对于一个大度数的顶点而言，三维结构在该顶点周围进一步拓展和优化的次数增多，从而能够在该顶点周围更大程度地计算出丰富和完整的三维点云，获得更好的三维重建效果。综上，本文算法在不同规模的数据集上都取得了相对更好的重建效果。

表3 各个算法在不同数据集上的重建效果Table 3 Reconstruction performance of algorithms on different datasets

图6 给出了4 种不同算法在数据集上多次实验后客观指标的平均表现。由图6(a)可知，在图像数量少时，各个算法的相机校准率相差不大，当数据集图像数量过百时，Colmap 和VSFM算法表现急剧下降，并且随着数据集图像数量的增多，相机校准率随之降低到不足10%，而openMVG 和本文算法能够保持接近100%的相机校准率，这说明openMVG 和本文算法能适应不同的数据集规模，在进行图像增量式重建时对于下一张最佳图像有较强的搜索能力，验证了本文基于候选集的下一张最佳图像评分方法的有效性。图6(b)给出了算法在不同数据集的点云生成数量。随着数据集图像数量增多，Colmap 和VSFM 算法生成的点云数量反而呈现总体下降的趋势，说明了这两种算法从多个视图中提取出三维信息的能力有欠缺，构建的点云结构数量不足，难以完成场景目标的重建任务。openMVG 和本文算法随着数据集图像数量的增多，始终保持了点云数量水平上升的趋势，本文算法在不同数据集上都生成了最多的点云数量，体现了本文算法较强的鲁棒性。由图6(c)可知，不同的算法随着数据集图像数量的增多，重建耗时的增量不同。其中Colmap 重建耗时平均增量最高，本文算法重建耗时的平均增量最低，在各个数据集上，本文算法比重建速度最慢的Colmap 平均重建耗时减少了58%，比openMVG 平均重建耗时减少了35%，比VSFM 平均重建耗时减少了19%。图6(d)给出了算法在不同数据集上点云生成速率的表现，其中Colmap 和VSFM 随着数据集规模增大，其点云生成速率急剧下降，本文算法则始终保持了较高水平的点云生成速率，综合各个数据集来看，本文比Colmap 的点云生成速率快了105%，比openMVG 快了25%，比VSFM 快21%，整体具有更高的重建效率。

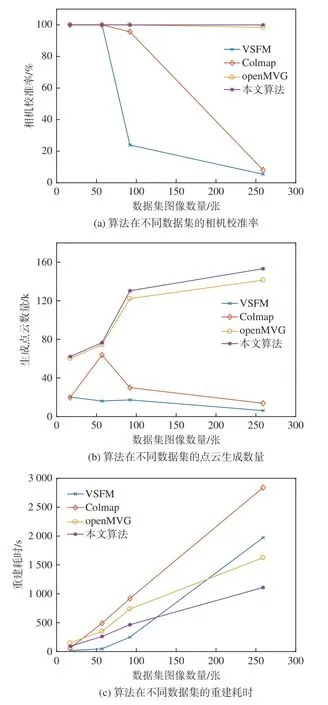
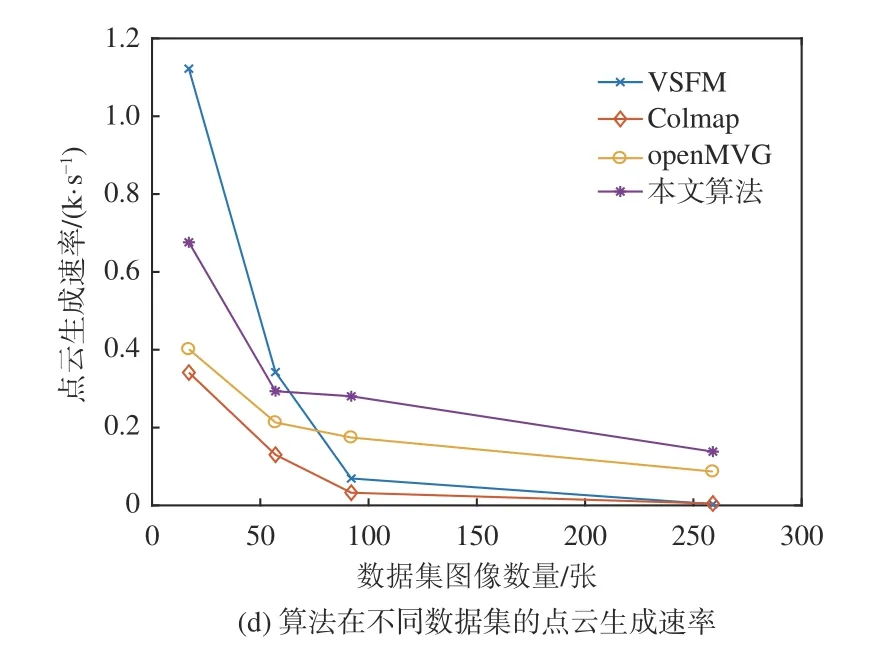
图6 算法在不同数据集上的客观指标表现Fig.6 Objective indicators performance of mentioned algorithm on different data sets

3 结论

本文提出了一种基于赋权连接图的增量式运动恢复结构算法。首先为赋权连接图设计了一种基于立体匹配质量的权重因子；其次在初始种子对的选择上，结合权重因子设计了一种度数感知的初始种子对优先级选择方法，能在全局搜索最佳的初始种子对；最后针对下一张图像的选择，提出了一种基于候选集的下一张最佳图像评分算法，算法先根据顶点的相邻关系获取下一张最佳图像的候选集，然后对候选集中的顶点根据其度数与匹配特征点分布均匀程度给予评分，并选择评分最高的作为下一张最佳图像。实验结果表明，相较于其他先进的增量式算法，本文提出的基于赋权连接图的增量式重建算法能够很好地适应不同规模的数据集，在保证了目标重建的完整性和重建效果的同时，在算法效率上取得了明显的领先优势。