1961—2020年黄河流域干旱演变分析和大气响应
刘玉针 魏长寿,2 李志进
(1.山东科技大学测绘与空间信息学院, 山东 青岛 266590;2.内蒙古科技大学矿业与煤炭学院,内蒙古 包头 014010)
干旱是影响人类社会的严重自然灾害之一,是指由区域水分收支或供求不平衡所引发的水分短缺现象[1]。由于水资源短缺和降水分布不平衡,黄河流域受干旱影响尤其严重[2]。21世纪以来,在全球变暖的大环境下,黄河流域干旱频发,河道萎缩,黄河下游干、支流断流严重。大尺度气象因子与干旱的响应在影响区域降水、温度的变化中起着重要作用。因此,探讨二者之间的遥相关性可以从大规模物理角度解释干旱的发生和长期变化趋势[3]。
张玉静等[4]和李军等[5]的研究说明,标准化降水蒸散发指数(Standardized Precipitation Evapotranspiration Index,SPEI)在我国南、北方均能够适应全球变暖大趋势下干旱的监测和评估。邹磊等[6]通过研究表明,SPEI能够灵活反映季节性干旱变化情况,并且与部分大尺度气候因子存在明显的相关性。张克新等[7]通过研究黄河流域极端气温的季节特征,发现流域的平均气温呈现较为显著的升温趋势,并且极端高温、低温与ENSO(El Nio-Southern Oscillation,厄尔尼诺-南方涛动)指数有显著相关性。杨肖丽等[8]利用标准化降水指数(Standardized Precipitation Index,SPI)对黄河流域干旱进行评估和预测,结果表明,21世纪初黄河流域干旱情势加剧,但在21世纪末干旱情势将有所减轻。但是,上述研究多注重从流域整体角度出发,探讨黄河流域干旱的时空变化特征,较少涉及从要素场层面提取时域和空域上的干旱特征信息,针对黄河流域干旱指数要素场分布模态的研究较少,鉴于此,笔者以标准化降水蒸散发指数(SPEI)为指标,采用分段线性回归、交叉小波变换和经验正交函数(Empirical Orthogonal Function,EOF)等方法探究流域干旱时空演变在年、季尺度上的特征,从干旱指数要素场层面探讨黄河流域干旱的时空分布模态,并结合大尺度气象因子,研究长期干旱与大气之间的遥相关性,以期为黄河流域干旱减灾和水土保持工作提供理论依据。
1 研究区概况
黄河发源于青藏高原,干流总长为5464km,自西向东流经青海、四川、甘肃、宁夏、内蒙古、陕西、山西、河南、山东共9个省(自治区),从山东东营注入渤海。黄河流域地势东低西高,自西向东跨越青藏高原、内蒙古高原、黄土高原和黄淮海平原4个地貌单元,黄河流域地理范围为东经95°53′~119°05′、北纬32°10′~42°50′,流域东西向跨越1900km,南北向跨越1100km,总面积79.5万km2,其中黄河内流区4.21万km2,共有8个二级流域分区(见图1)[9]。黄河流域降水量呈现由上游到下游,由西北到东南递增的趋势。全流域多年平均降水量(1956—2019年)为452.1mm,其中上游为390.4mm,中游为523.7mm,下游为644.7mm,空间差异性十分明显[10]。在全球变暖的大环境下,黄河流域干旱频发。

图1 黄河二级水系流域分区
2 资料及方法
本文使用中国气象数据网提供的“中国地面气候资料月值数据集V3.0”,选取黄河流域1961—2020年数据完整性较好的90个气象站点的逐月气温和降水实测数据。研究区高程及气象站点分布见图2。在数据分析处理过程中,对于个别数据缺测的站点,采用均值替补法将其数据补全。使用全球大尺度气候因子调查长期干旱变化的物理原因,从NOAA获取大尺度气象因子月值数据,包括大西洋年代际振荡( Atlantic Multidecadal Oscillation, AMO)、北极涛动(Arctic Oscillation,AO)、北大西洋涛动(North Atlantic Oscillation,NAO)、北太平洋遥相关指数(North Pacific,NP)、太平洋年代际振荡(Pacific Decadal Oscillation,PDO)、多元ENSO指数(Multivariate ENSO Indicator,MEI)和南方涛动指数(Aouthern Oscillation Index,SOI)。
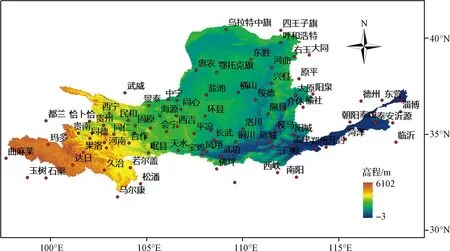
图2 研究区高程及气象站点分布
2.1 标准化降水蒸散指数
近年来,在研究区域干旱时空分布特征和干旱预测等方面,帕尔默干旱指数(Palmer Drought Severity Index,PDSI)和标准化降水指数(SPI)[11-12]被广泛应用。SPEI由Vicente-Serrano等人在2010年提出,Beguería等人在2014年改进,是在SPI的理论基础上,把潜在蒸散发对干旱的影响也加以考虑[13],SPEI是全球变化背景下监测和评估干旱的理想指标[14]。SPEI除了继承SPI空间一致性和多时间尺度的优点,又考虑到了潜在蒸散发对干旱的影响,从而能够更好地发挥对干旱的监测和评估作用。计算SPEI涉及的主要指标及公式如下[14]:
(1)
Di=Pi-PETi
(2)
(3)
(4)
(5)
(6)
(7)
(8)
式中:PETi为第i月潜在蒸散量,mm;Pi为月降水量,mm;Ti为月平均温度,℃;H为年热量常数;m为常数,m=0.49+0.179H-0.0000771H2+0.000000675H3;α为尺度函数;β为形状函数;γ为origin参数;P为累计概率密度;F(x)为log-logistic概率分布的累计函数;Γ为阶乘函数;ω0、ω1、ω2为数据序列Di的概率加权矩;c0、c1、c2、d1、d2、d3均为常数;ω为距离加权矩。若P≤0.5,则P=F(x);若P>0.5,则P=1-F(x)。
因此,本文以SPEI为指标,分析黄河流域1961—2020年干旱的时空变化特征。相关研究表明,可以根据SPEI值的大小将干旱分为5个等级(见表1)。

表1 SPEI干旱等级划分标准
SPEI具有1个月、3个月、6个月和12个月的时间尺度。其中,季节性干旱可以通过3个月时间尺度的SPEI值进行研究[15]。因此,3—5月、5—8月、8—11月、11月至次年2月的SPEI-3值可以分别表示研究区域春、夏、秋、冬季的干旱指数,可用于分析流域干旱在季节尺度上的特征[16]。
2.2 Mann-Kendall检验与Sen’s趋势分析
Mann-Kendall(M-K)检验被应用于检测时间序列的趋势。其优点是数据缺测值对计算结果影响不大,且无须验证待分析数据是否为某一分布[16]。Sen’s趋势分析法的优点在于计算结果不受少数异常值的干扰,数据误差对其计算结果影响较小,计算过程中原始数据不需要服从特定分布,其显著性水平来源于Mann-Kendall检验[17]。因此,笔者将Mann-Kendall检验与Sen’s趋势分析相结合,探究研究区域长时间序列SPEI指数的变化趋势。
2.3 经验正交函数分析法
经验正交函数分析法(EOF)用于提取数据结构特征。1950年第一次用作研究气象的算法,目前被广泛应用于地学和水文气象学,EOF分析的目标是将时空数据集转化成要素场的空间模态和与之相对应的时间系上的投影[18]。
2.4 交叉小波变换
交叉小波变换(Cross-wavelet Transform,XWT)可以研究两个长时间序列之间的时频关系[19]。本文使用交叉小波变换分析研究SPEI指数与大尺度气象因子之间的关系。
3 结果与分析
SPEI除了具有空间一致性和多时间尺度的优点外,又考虑到了潜在蒸散发对干旱的影响。研究SPEI指数在黄河流域的时空分布特征和SPEI要素场的分布特征,可以很好地为黄河流域水文预报、水资源评估、干旱减灾等提供有力的技术支持。
3.1 干旱指数的时空分布特征
3.1.1 时间分布特征
1961—2020年黄河流域年尺度SPEI变化见图3(a)折线,其趋势线见图3(a)实线。年尺度的SPEI下降幅度为0.102/10a,说明1961—2020年流域内有明显干旱倾向。其中,1964年最湿润(SPEI=1.557),1997年最干旱(SPEI=-1.121)。由图4(a)可见,2006年之前黄河流域干旱化趋势日益严重,2006年之后干旱情况有所缓解,但流域内总体仍呈现干旱趋势。
图3(b)~图3(e)显示了黄河流域1961—2020年季节尺度SPEI变化及其趋势线。春季SPEI指数下降幅度为0.087/10a,干旱化趋势明显,其中,2000年最干旱(SPEI=-1.464),1990年最湿润(SPEI=1.179);夏季SPEI指数下降趋势较显著,下降幅度为0.038/10a,其中,1997年最干旱(SPEI=-1.063),1964年最湿润(SPEI=0.975);秋季SPEI指数下降幅度为0.091/10a,其中,1998年最干旱(SPEI=-1.815),1961年最湿润(SPEI=1.445);冬季SPEI指数显示上升倾向,上升幅度为0.073/10a,呈轻微湿润化趋势,其中,1998年最干旱(SPEI=-1.634),1989年最湿润(SPEI=1.433)。利用分段线性回归分析发现,1961—2020年季尺度和年尺度SPEI指数均未发生显著性突变,见图4(b)~图4(e)。
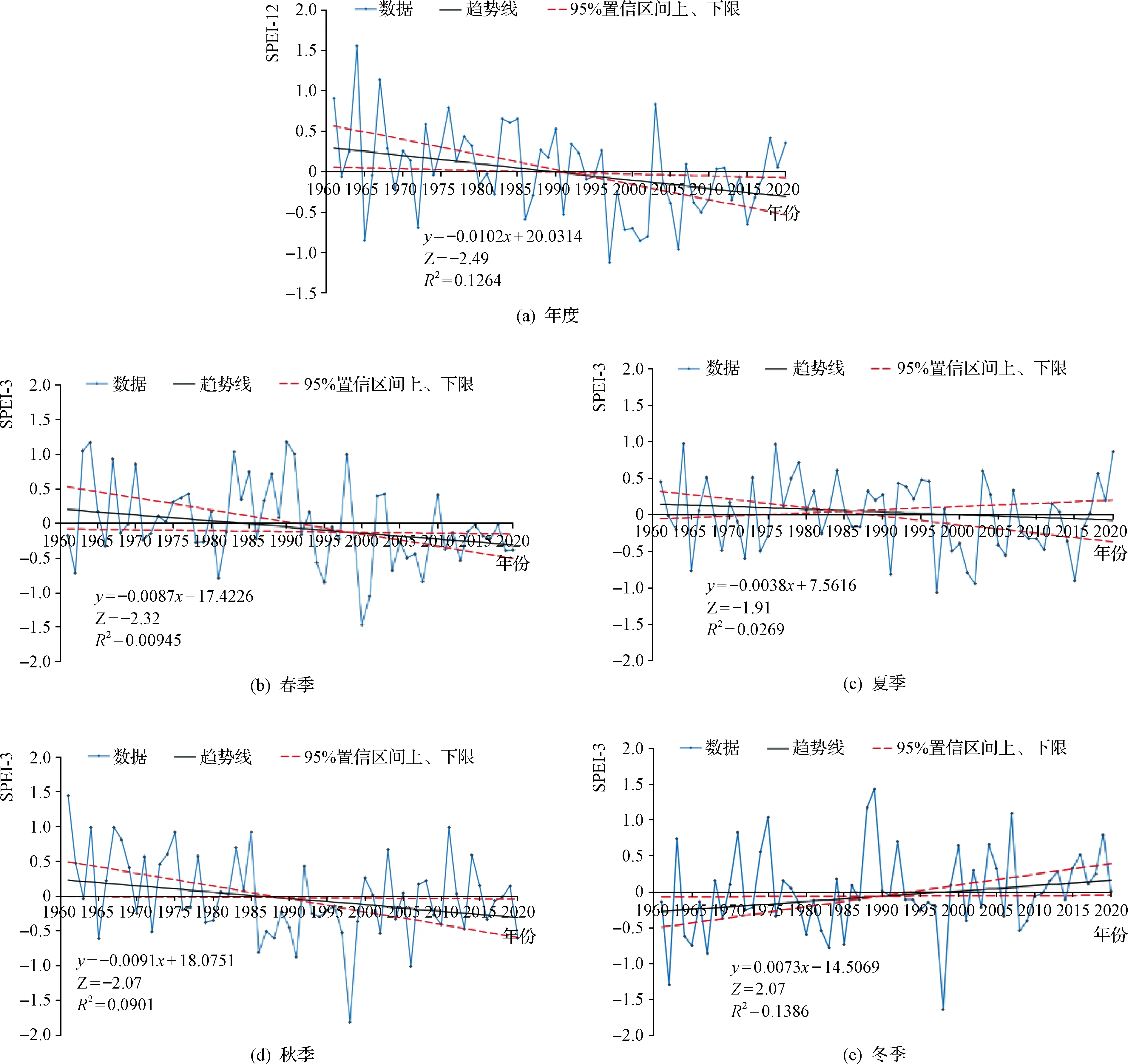
图3 黄河流域1961—2020年年度及季度SPEI指数变化及其趋势线
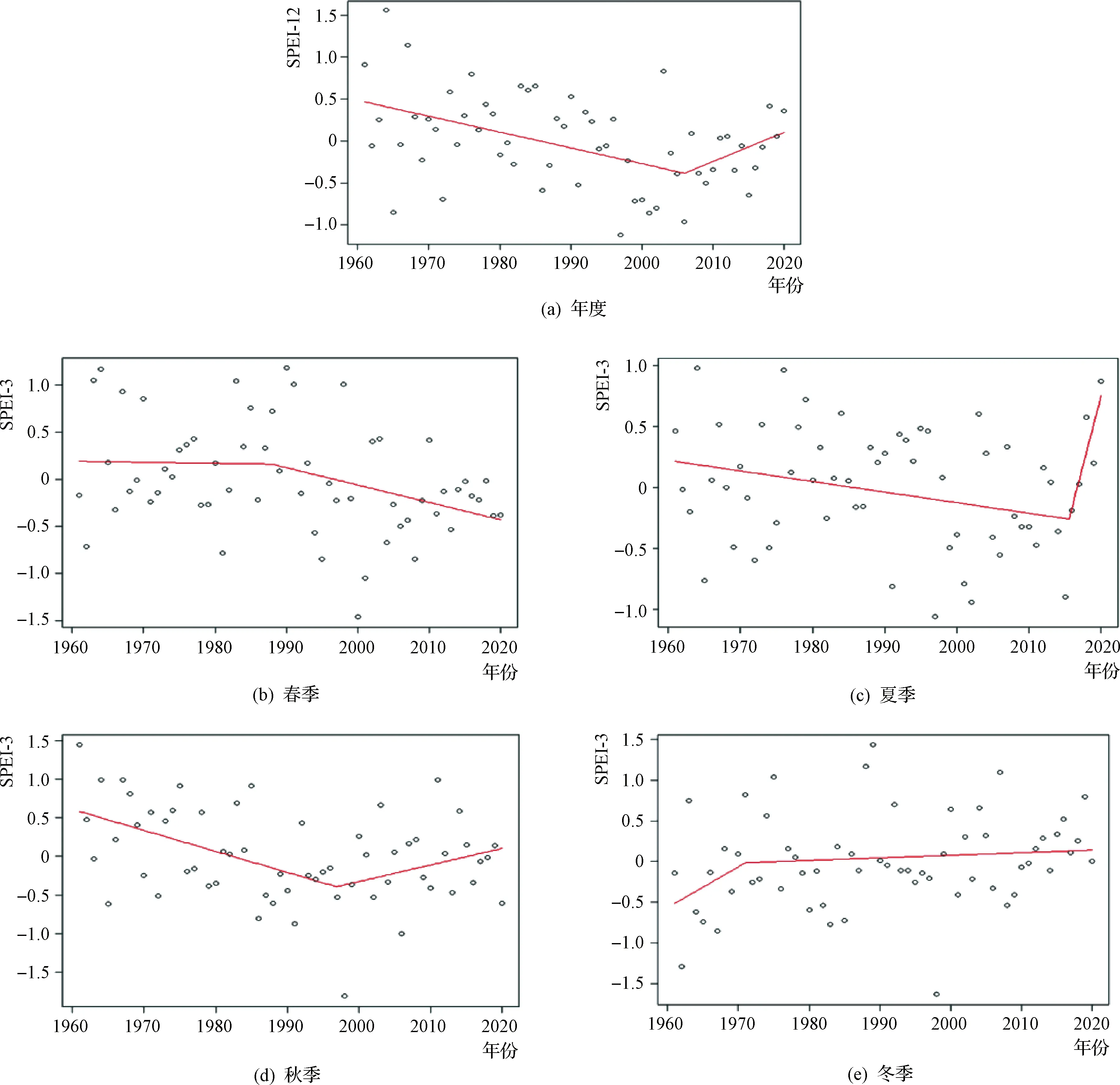
图4 黄河流域1961—2020年年度及季度SPEI指数分段线性回归
综上,从季度上看,秋季干旱趋势最强,春、夏季次之,冬季最弱。从年度上看,自2006年以来,黄河流域干旱情况有所缓解,但总体仍呈现干旱化趋势。
3.1.2 空间分布特征
图5是1961—2020年黄河流域年度及季度干旱指数变化倾向率的空间分布图。从图5(a)可看出,黄河流域年度SPEI指数在空间上存在一定分异性,以景泰—固原—临夏—合作线为界,西部地区显示极微弱的干旱趋势,东部地区呈现干旱趋势。总体上看,年度SPEI指数显示流域表现为干旱趋势,尤其是流域内兰州至河口镇区域、龙门至三门峡区域和内流区。图5(b)~图5(e)分别显示了流域SPEI指数春、夏、秋、冬季的空间变化趋势。春季,以中宁—同心—海源—西吉—天水线为界,除流域中部兰州至河口镇区域、龙门至三门峡区域、内流区、河口镇至龙门区域呈现干旱趋势外,其他地区显示为湿润化。夏季,流域兰州至河口镇区域显示干旱加剧,龙羊峡以上区域、三门峡至花园口区域和花园口以下区域表现为轻微干旱趋势。秋季,流域内以合作—景泰—佛坪线为界,自西向东分别呈现湿—干—微湿趋势。冬季,黄河流域以鄂托克旗—横山—长武线为界,流域东北部显示为干旱化,其余地区以轻微干旱为主。
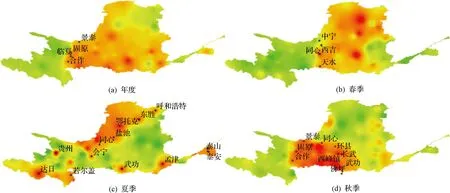
图5 黄河流域1961—2020年年度及季度SPEI指数空间变化趋势
3.2 干旱发生频率的分布特征
1961—2020年黄河流域年度及季度干旱发生频率的空间差异见图6。从时间上看,在年尺度上,黄河流域干旱发生频率为25.0%~38.3%,其中特旱发生频率为0~3.3%,重旱发生频率为0~10.2%,中旱发生频率为3.3%~20.0%。可见,干旱发生频率与干旱等级呈负相关。在季节尺度上,春、夏、秋、冬季干旱发生频率分别为26.7%~40.0%、25.1%~40.0%、25.1%~40.0%和23.3%~41.7%,不同等级的干旱发生频率无明显差别。
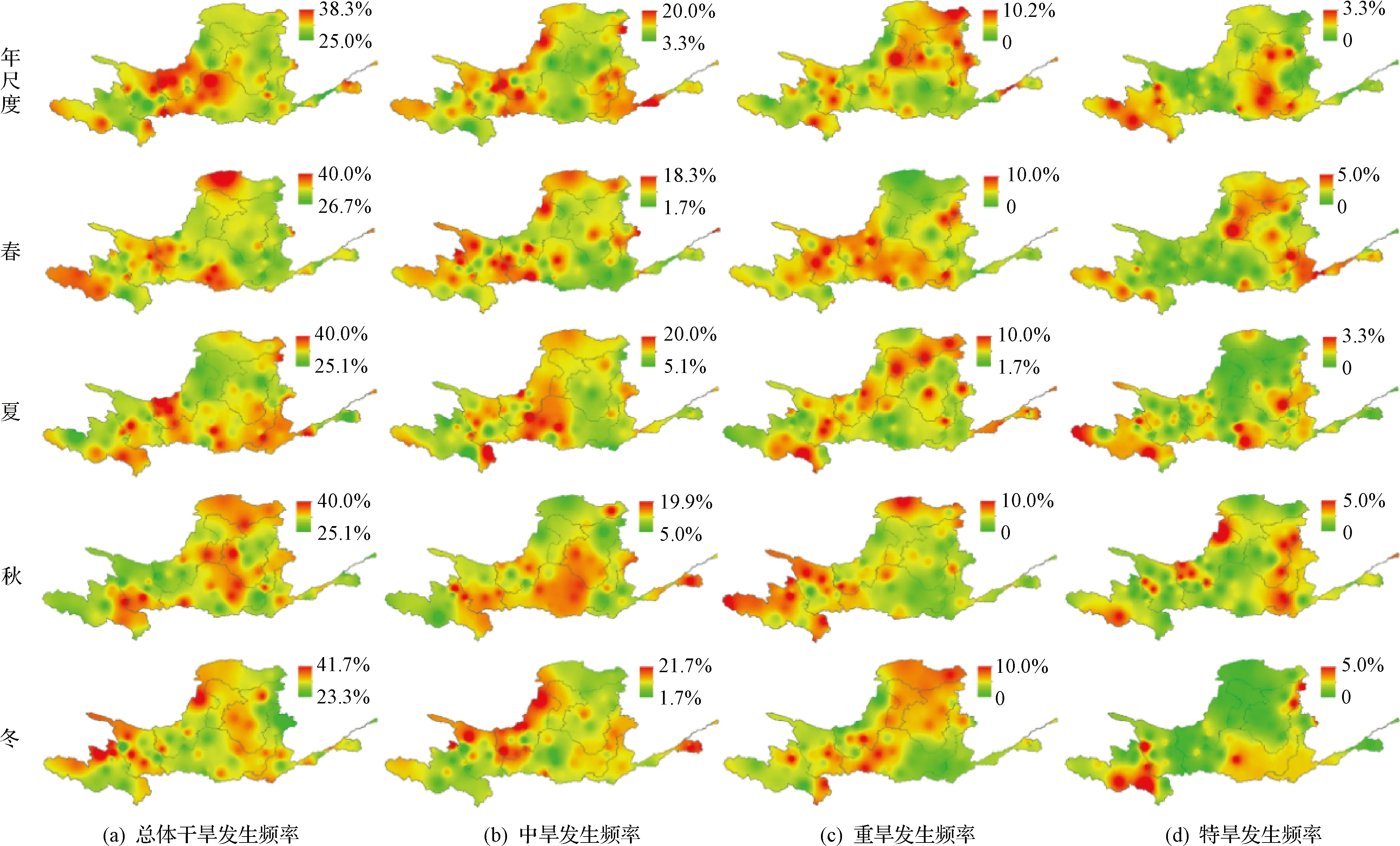
图6 不同等级干旱发生频率分布
从空间上看,年尺度和季尺度干旱发生频率的空间分布有显著差异。在年尺度上,其干旱发生频率较高的区域集中分布在龙羊峡至兰州的东北部地区、兰州至河口镇的西南部地区和龙门至三门峡的西北部地区;春季干旱发生频率较高的区域分别为龙羊峡以上的西部地区、兰州至河口镇的北部地区、龙门至三门峡南部的宝鸡及其周边区域;夏季干旱发生频率较高的地区分散分布在流域南部和东南部地区;秋季干旱发生频率较高的区域主要分布在黄土高原部分地区和青藏高原东部地区;冬季干旱发生频率较高的区域主要集中分布在流域西北部和黄土高原部分地区。
3.3 黄河流域干旱时空模态分析
3.3.1 空间分布模态分析
应用EOF分解1961—2020年年度SPEI要素场,得到时域和空域分布特征,用North检验检测特征值的显著性,从而确定要素场的空间分布模态。由EOF分解得到的特征向量虽然不能代表SPEI指数的大小,但是它可以通过特征向量的大小反映流域的干湿变化程度。由表2可见,前两个主要特征向量的特征根误差范围不产生重叠,满足随机性要求,通过North显著性检验,其累计方差贡献率为52.14%。因此,可用前两种空间模态解释黄河流域干旱的主要空间分布特征。
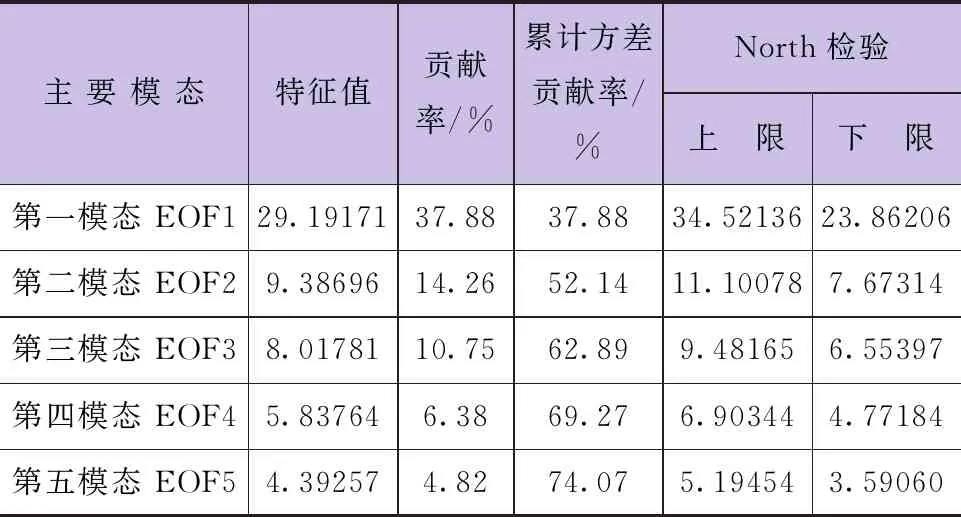
表2 黄河流域年尺度SPEI指数EOF分解的前5个特征向量贡献率
图7的EOF1是第一特征向量图,其方差贡献率为37.88%,是年度SPEI要素场的主要空间分布。可见,第一特征向量的空间分布模态均为负值,表明流域内干湿演变类型一致,整体干旱或整体湿润。其低值中心集中分布在龙羊峡至兰州、兰州至河口镇和内流区域,说明在全流域干旱或湿润时,这3个地区表现程度更明显。
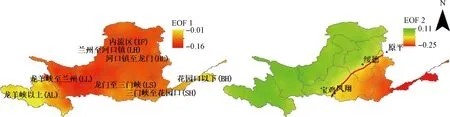
图7 年尺度SPEI场的特征向量空间分布模态
图7的EOF2是第二特征向量图,其方差贡献率为14.26%,也是年度SPEI要素场的一种空间分布。EOF2既有正值也有负值,该分布类型在空间上大致以原平—绥德—宝鸡线为界,以东为负值,以西为正值,呈现东西反向分布的情况。在EOF2的影响下,黄河流域以原平—绥德—宝鸡线为界呈现“西湿东干”或“西干东湿”分布。
综上所述,黄河流域1961—2020年年尺度SPEI要素场主要有2种,即由EOF1决定的全区一致型和由EOF2决定的东西反向型。
3.3.2 时间分布模态分析
时间系数与特征向量相对应,特征向量又决定着要素场的空间分布[18]。因此,要素场空间分布类型的时间变化可以通过时间系数表示,其方向由时间系数的符号表示,负号表示与分布类型相反,正号则相同。系数绝对值越大,说明该时刻该分布类型越典型[18]。根据空间分布特征分析,黄河流域1961—2020年年尺度SPEI要素场主要有2种,每种要素场有2种表现类型:EOF1决定全年全流域整体干旱和整体湿润2种类型;EOF2决定流域内以原平—绥德—宝鸡线为界,东部湿润西部干旱和西部湿润东部干旱2种类型。
分析黄河流域SPEI要素场的4种空间分布类型,年度SPEI要素场的空间分布类型用该年PCs绝对值最大值对应的EOFs表示[18]。EOF1和EOF2的时间系数及其变化趋势见图8。
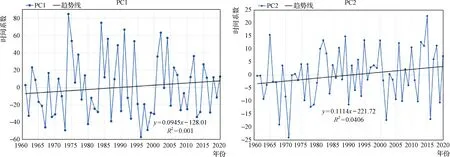
图8 前两个空间模态的时间系数
经分析得到:全年全流域干旱的为24年,全年全流域湿润的为22年。以原平—绥德—宝鸡线为界,东湿西干的空间分布类型有6年,西湿东干的空间分布类型有8年。可见,近60年,年SPEI要素场以第一模态为主,有46年之多,占总年数的76.67%,且全年全流域干旱的总年数大于全年全流域湿润的总年数,表明黄河流域1961—2020年呈现干旱发生加剧的趋势。时间系数反映的SPEI要素场时空分布与特征向量贡献率所反映的年SPEI要素场时空分布基本一致。
3.4 干旱与气象因子的响应
计算全球大尺度气象因子数据(SOI、PDO、NP、NAO、AO、AMO、MEI)和黄河流域年尺度SPEI以及PCs之间的Pearson相关系数,基于相关系数探讨它们之间的关系。研究1961—2020年共60年数据,在α=0.05的条件下,t检验单尾临界值约为0.271。由表3可知,SPEI、PC1与MEI相关性最高,NAO次之;PC2与PDO相关性最高,NAO次之。总体表明黄河流域干湿程度与大尺度气象因子MEI、NAO和PDO具有较强的相关性。
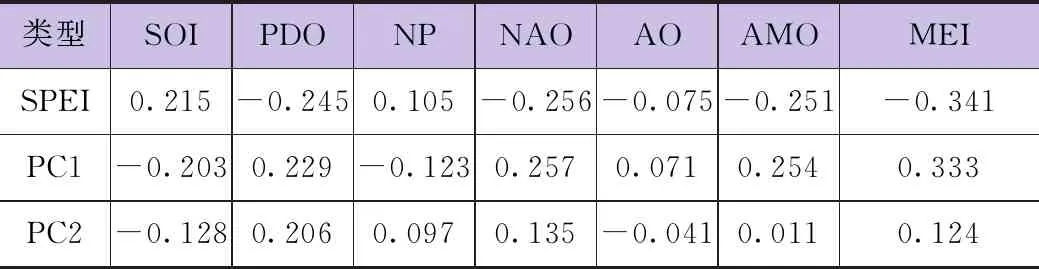
表3 大尺度气候因子与SPEI及PCs相关系数
分别对黄河流域年尺度SPEI与MEI、NAO,第一模态时间系数PC1与MEI、NAO,第二模态时间系数PC2与PDO、NAO进行交叉小波变换分析,研究各时间序列在时域、频域中的关系,结果见图9。图中,被黑色实线包围的范围表示通过95%置信水平的检验,箭头向左为负相关,箭头向右为正相关[19]。从图9可看出,MEI与SPEI和PC1的计算结果相近,这也说明主要由EOF1决定流域的干旱或湿润情况。MEI与SPEI有两个显著性共振周期,分别是1965—1973年的2~4年周期和1982—1989年的4~6年周期,MEI与PC1的共振周期与此相同。NAO与SPEI有两个显著性共振周期,分别是1971—1976年的1~2年周期和2001—2010年的7~8年周期,NAO与PC1只有1970—1976年的1~2年周期。PDO与PC2在1995—2002年存在2年左右的显著性共振周期,NAO与PC2在1999—2012年存在5~8年共振周期。其中,SPEI与MEI和NAO均为负相关,PC1与MEI和NAO也为负相关,即SPEI或PC1值越小,与其相对应的MEI和NAO越大,干旱程度越严重,黄河流域内遭受的干旱事件越多。PC2滞后于PDO和NAO时间序列1/4个周期,即PC2所表征的干湿情况要比PDO和NAO表征的事件晚发生。
4 结 论
本文选取黄河流域90个气象站点近60年的实测降水量和气温月值数据,以SPEI为指标,利用M-K检验、Sen’s趋势分析、分段线性回归、交叉小波变换和EOF等方法研究黄河流域年、季尺度SPEI的时空演变特征和近60年干旱的分布模态,并结合气象因子,研究了长期干旱与大气之间的遥相关性。得出以下结论:
a.在过去1961—2020年共60年间,黄河流域整体表现为干旱。结合M-K检验和Sen’s趋势分析,总体而言,流域在秋季干旱加剧趋势最显著,春季和夏季次之,冬季最弱,甚至有出现轻微湿润化的可能,年度和季节SPEI指数的空间分布存在一定的分异性。
b.黄河流域年尺度干旱发生频率为25.0%~38.3%,干旱发生频率与干旱等级呈负相关。不同季节,发生干旱的频率无明显差异。在年度和季度上干旱频率的空间分布有较大差异。
c.经验正交函数(EOF)分析表明,黄河流域年度SPEI指数要素分布场主要有两种模态:全区一致型和东西反向型。其中,全区一致型表现为流域整体干旱或整体湿润的特征,第一模态特征向量贡献率为37.88%,是黄河流域年尺度SPEI要素场的主要控制模态;东西反向型表现为流域内以原平—绥德—宝鸡线为界,东部湿润西部干旱和西部湿润东部干旱两种类型。第二模态特征向量贡献率为14.26%。结合时间系数序列分析,黄河流域干湿分布特征受第一模态控制的有46年,其中有24年为干旱年份,说明黄河流域呈现整体干旱趋势。
d.通过计算SPEI和PCs与大尺度气象因子(SOI、PDO、NP、NAO、AO、AMO、MEI)之间的Pearson相关系数,发现表征ENSO事件的多元ENSO指数(MEI)与SPEI的相关性最高,NAO和PDO次之。利用交叉小波变换分析得到,SPEI与MEI和NAO均为负相关关系,PC1与MEI和NAO也为负相关关系,即SPEI值越小,与其相对应的MEI和NAO越大,干旱程度越严重,黄河流域内遭受的干旱事件越多。
本文采用SPEI指数得出的黄河流域近60年干旱特征值与黄婷婷等[20]的研究结果一致,表明SPEI指数能够很好地反映出黄河流域不同季节、不同时间尺度的干旱时空演变特征。影响干旱的因素众多,本文仅探究了气温、降水和大尺度气象因子对黄河流域干旱演变的影响,没有考虑风速、净辐射量、温度等因素的影响。因此,今后应从更加深入的角度分析其他因素对流域干旱演变的影响。

