多相永磁同步电机磁场解析建模与容错性能分析

王厚军

(安徽华电芜湖发电有限公司，安徽 芜湖 241000)

0 引 言

与传统的三相永磁电机相比，多相永磁电机具有功率密度高、可靠性高、冗余度大等优势，在电机系统发生故障时，仍能保持系统所需的工作性能；同时，其还具备故障隔离和抑制能力[1-3]。因此，多相永磁电机在航空航天[4]、船舶推进[5]、风力发电[6]和电动汽车[7]等可靠性要求高的领域引起了广大学者的关注。

文献[8]建立了单相断开的5相永磁同步电机(PMSM)的解耦数学模型，并实现了容错矢量控制；为了抑制永磁体谐波磁链引起的转矩脉动，采用速度环滑模控制方式，但会引起系统抖动，增加电流谐波含量。文献[9]基于矢量控制，对单相短路故障后的电流控制策略进行分析，通过对角度变换进行优化实现电机模型的解耦，从而有效地抑制了转矩脉动。文献[10]提出了一种基于电压前馈补偿的矢量控制策略，从而减小了多相电机的转矩脉动。文献[11]针对航天器用5相PMSM绕组开路故障时转矩脉动大和谐波电流含量大的问题，提出一种改进的容错式直接转矩控制算法。文献[12]提出了绕组故障前后平均电磁输出转矩保持不变的容错控制策略，通过重新优化各相绕组电流的幅值和相位，实现了控制系统的满负荷运行。文献[13]以相绕组最大电流为约束条件建立12相PMSM的容错控制策略，提高了PMSM缺相时输出转矩的可靠性。文献[14]针对5相永磁无刷电机的单相开路故障提出一种不对称空间矢量脉宽调制(SVPWM)控制方法，有效降低了故障运行时电流谐波含量，但该方法不适用于两相开路故障。上述文献只是针对多相电机故障发生时，对电磁转矩、转矩脉动等性能进行了容错分析，并未考虑电机故障运行下，电机的温升是否达到极限，尤其对于高功率密度多相PMSM，局部温升过高的问题更为突出。在现有的研究基础上，对多相电机故障容错运行下的温度场分布情况进行了考核。同时，为了准确、快速计算电机的电磁性能参数，国内外学者对永磁电机的磁场解析计算进行了大量的研究。文献[15-20]分别对开口槽、半开口槽、定子表面开设辅助槽、分块式Halbach型磁极结构、磁极偏心结构以及永磁体埋入式结构等表贴式永磁同步电机(SPMSM)进行了磁场解析计算，详细分析了空载气隙磁密、齿槽转矩以及反电动势等电磁参数。但是少有文献针对多相PMSM在绕组断路等故障模式下的电机的容错性能进行解析建模计算。

本文以一台对称12相SPMSM为研究对象，建立了多相内转子SPMSM绕组缺相不对称运行下的空载与负载磁场解析计算模型，并通过有限元分析和试验测试对磁场解析模型的准确性进行了验证。在此基础上，以最小等值相电流为优化目标，建立了多相电机驱动系统在电机绕组断路等故障模式下的容错控制策略，并对绕组不对称运行下电机电磁性能进行了深入分析。

1 建立磁场解析模型

1.1 建立矢量磁位方程组

图1给出了内转子SPMSM的子域模型示意图，在二维极坐标系中，将电机划分为4部分子域，分别为：永磁体、气隙、定子槽口以及定子槽。图中R1为永磁体内半径，R2为永磁体外半径，R3为定子内径，R4为槽口表面半径，R5为定子槽底半径，β为定子槽宽角，δ为槽开口角度。为了便于解析计算，做出以下假设：

(1) 定、转子铁心材料的磁导率无穷大；

(2) 二维极坐标系中，不考虑电机端部效应；

(3) 各求解区域均为形状规则的扇形或圆环形结构。

求解空载气隙磁场计算时，定子槽中无电流，各子域内矢量磁位满足以下方程组：

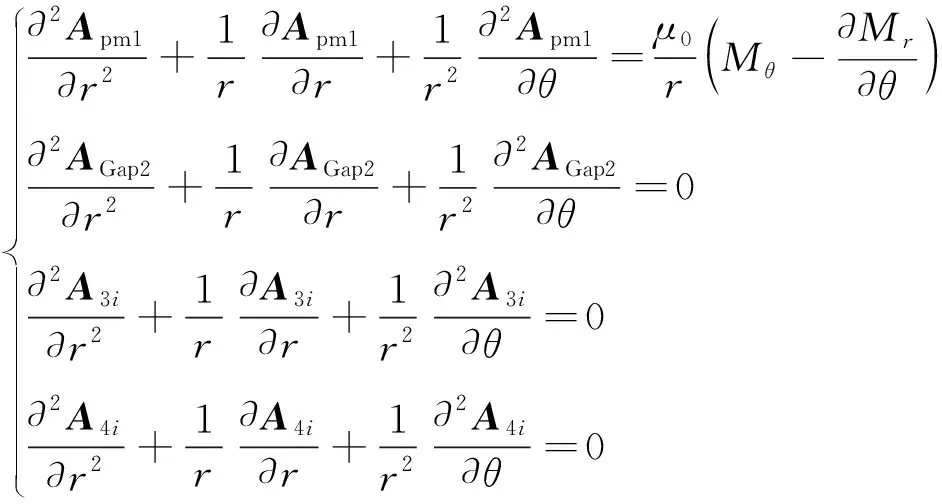
(1)

式中:i为定子槽序号；Apm1为永磁体子域1中的矢量磁位；μ0为空气相对磁导率；Mr和Mθ分别为永磁体剩余磁化强度的径向和切向分量；AGap2为气隙子域2中的矢量磁位；A3i为定子槽口子域3中的矢量磁位；A4i为定子槽子域4中的矢量磁位。

基于分离变量法建立各子域的拉普拉斯方程或泊松方程，根据边界条件确定通解中的谐波系数，得到各子域中的矢量磁位解析表达式。

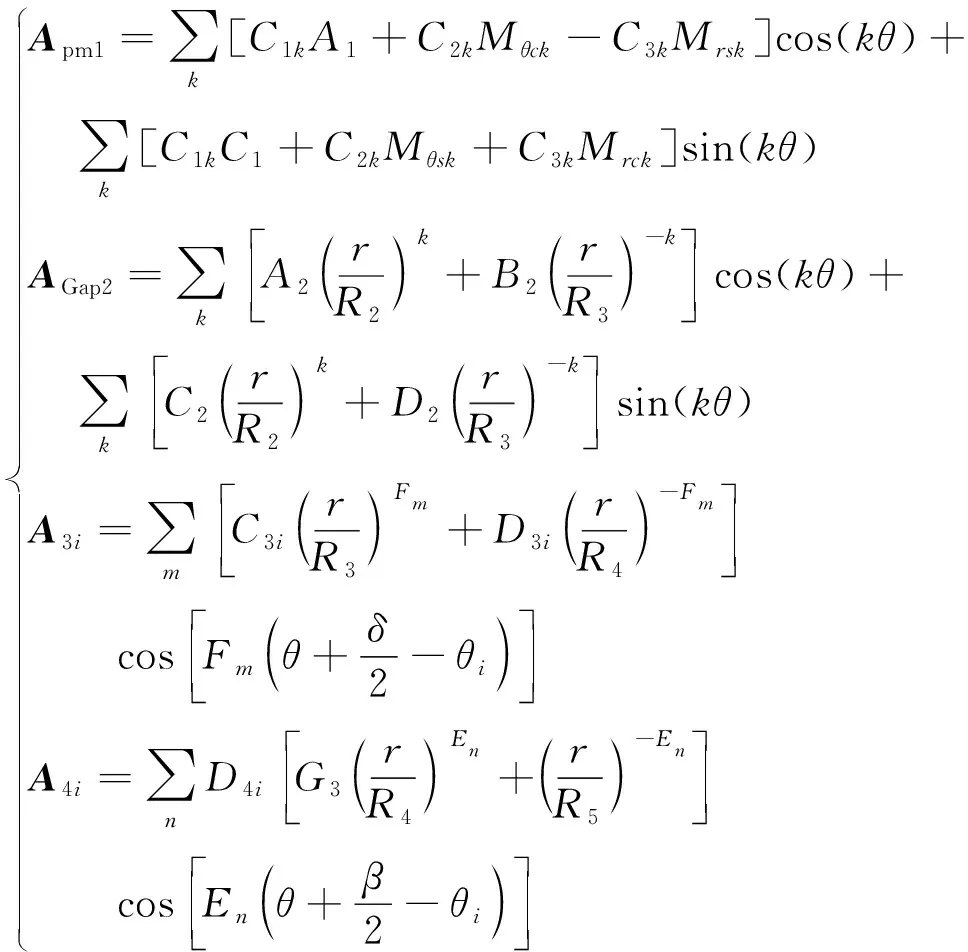
(2)

式中：A1、C1、A2、B2、C2、D2、C3i、D3i和D4i为矢量磁位中的谐波系数，可以通过各子域间的交界面条件，即交界面上的法向通量密度与切向矢量磁位的连续性来确定。k、m和n为谐波次数；G3、Fm、En为中间变量，无具体物理意义；C1k、C2k、C3k、Mθck、Mθsk、Mrck、Mrsk、Fm和En的详细推导过程在此不做详述，详见文献[15-16]。

1.2 建立矢量磁位方程组

(1) 永磁体与气隙交界面条件。

在永磁体与气隙的交界位置，即永磁体半径R2处，根据径向磁通密度连续性和切向磁场强度连续性，可得各子域之间的分界面条件，进而求解谐波系数。

Apm(R2,θ)=AGap2(R2,θ)

(3)

H1θi(R2,θ)=H2θi(R2,θ)

(4)

(2) 气隙与定子槽口交界面条件。

在定子槽与槽口的交界位置，即半径R3处：

A3i(R3,θ)=AGap2(R3,θ)

(5)

H2θi(R3,θ)=H3θi(R3,θ)

(6)

(3) 定子槽与定子槽口交界面条件。

在定子槽口与气隙的交界位置，即半径R4处：

A4i(R4,θ)=A3i(R4,θ)

(7)

H4θi(R4,θ)=H3θi(R4,θ)

(8)

式中：H1θi、H2θi、H3θi、H4θi分别为永磁体、气隙、第i个槽口和槽的磁场强度。

将上述得到的各子域之间的交界面条件作傅里叶级数展开，并联立方程组，可求得各个子域矢量磁位表达式中的谐波系数。

1.3 电磁性能计算

根据矢量磁位与磁通密度的关系，可以得到气隙子域2中径向和切向的空载气隙磁通密度如下所示：

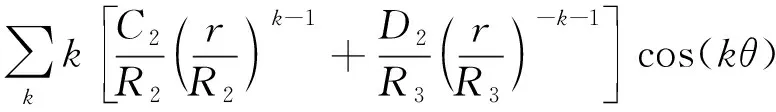
(9)

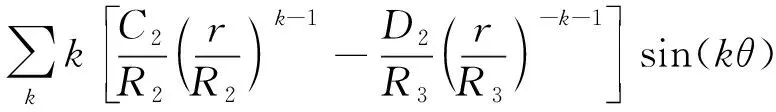
(10)

假设定子槽中绕组上下分布且均匀，基于斯托克斯定理，在某一个转子位置，采用定子槽的矢量磁位，可以求得在给第i槽中上下层绕组的磁链为

(11)

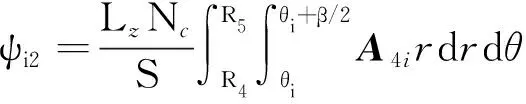
(12)

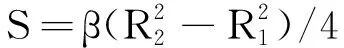
(13)

式中:lz为电机轴向长度；Nc为绕组线圈匝数；S为绕组截面积。

以A相绕组为例，上下层绕组线圈在定子槽中的分布，可以定义为矩阵C1和C2：

C1=[Ccell_1…Ccell_1]1×ξ

(14)

C2=[Ccell_2…Ccell_2]1×ξ

(15)

Ccell_1=

[0 1 -1 0 0 0 0 0 0 0 0 0 0 -1 1 0 0 0 0 0 0 0 0 0]

(16)

Ccell_2=

[-1 1 0 0 0 0 0 0 0 0 0 0 1 -1 0 0 0 0 0 0 0 0 0 0]

(17)

式中:Ccell_1和Ccell_2为一个单元电机下的上下层绕组分布情况，本文中单元电机数ξ=2。

因此，可得A1相绕组磁链和反电动势如下所示：

φA1=C1[ψ1,1,…,ψ1,48]T+C2[ψ2,1,…,ψ2,48]T

(18)

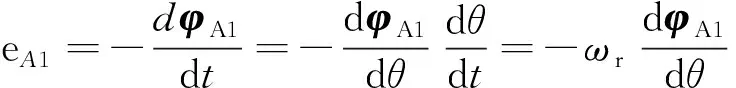
(19)

式中：ωr为机械角速度。

在准确求解e1-e2-e3-e4-e5-e6-e7-e8-e9-e10-e11-e12对称12相空载反电动势的基础上，可以得到多相PMSM的电磁输出转矩为

Tem=(e1i1+e2i2+e3i3+e4i4+e5i5+e6i6+e7i7+

e8i8+e9i9+e10i10+e11i11+e12i12)/ωr

(20)

式中：i1、i2…i10、i11、i12分别为对称12相绕组相电流。

2 磁场计算与有限元验证

以一台船舶用44极48槽12相对称SPMSM为例，对本文建立的磁场解析模型进行二维有限元仿真验证，表1给出了SPMSM部分设计参数。本文所研究的对称12相SPMSM各相定子绕组互差π/6，定子绕组轴线相对位置如图2所示。

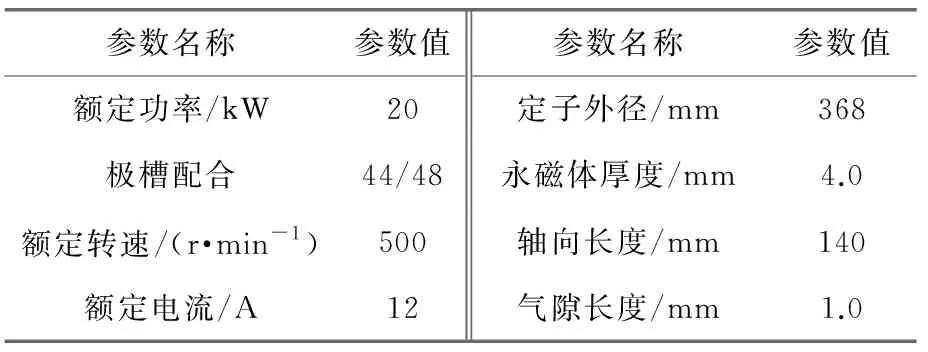
表1 SPMSM部分设计参数

取气隙中间位置处，图3给出了解析法和有限元仿真计算得到的1/4圆周下径向磁密波形对比图。计算结果显示,两种计算方法的吻合度很高，径向气隙磁密有效值分别为0.75 T和0.73 T，与有限元法相比，有效值计算误差仅为2.7%。图4给出了两种计算方法下的切向气隙磁密波形对比图，两种计算方法的波形畸变率分别为21.2%和22.7%，误差较小。

为了同下文中试验测试得到的线空载反电动势波形进行对比，图5给出了基于解析法和有限元仿真计算得到的线空载反电动势波形曲线，两种计算方法的有效值分别为335.5 V和330.9 V，计算误差为1.4%。并对前25次谐波进行了快速傅里叶变换(FFT)分析，得到波形畸变率分别为2.9%和2.5%，各次谐波对比如图6所示，基波幅值分别为471.5 V和465.5 V，5次谐波幅值最高分别为7.0 V和8.9 V。

图7给出了各相绕组无故障状态下的电磁转矩波形对比图，解析法和有限元仿真计算得到的平均电磁转矩分别为392.4 N·m和390.1 N·m，电磁转矩脉动分别为2.1%和0.7%，解析法略高于有限元仿真。图8给出了对称12相SPMSM在任意一相绕组断路情况下的电磁输出转矩波形对比图。

以第1相和第2相以及第1相和第3相绕组断路为例，图9分别给出12相绕组在任意2相绕组断路故障状态下的电磁输出转矩波形对比图。2相绕组断路共分为5种情况，分别为第1相和2相、第1相和3相、第1相和4相、第1相和5相以及第1相和6相断路，认为故障相绕组电流为0，其余各相绕组中的电流和反电动势正常工作。表2给出了任1相或任2相绕组断路状态下，SPMSM的平均输出电磁转矩以及转矩脉动，结果显示与有限元仿真相比，本文所建立的绕组不对称运行下磁场解析建模计算精度较高；当电机发生缺相故障时，电磁转矩明显降低且转矩脉动增大；在第1相和第4相绕组断路状态下PMSM的转矩脉动远小于其他几种情况。

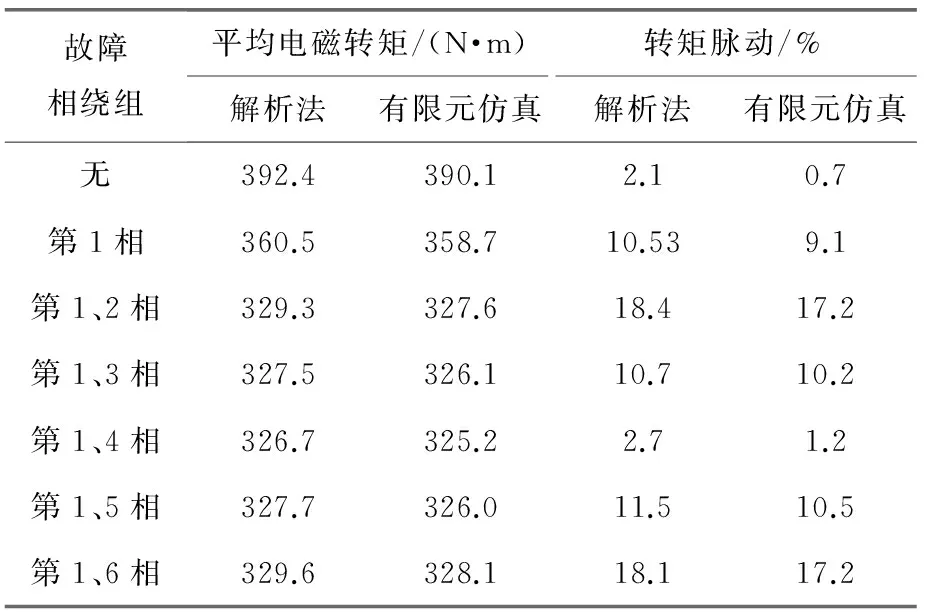
表2 任1相或任2相绕组断路状态下电磁性能

3 绕组不对称运行下的容错性能分析

电机运行工作时，电机及驱动电路中的电子器件都可能发生故障，通过故障检测以及故障隔离，可以把故障转化为缺相故障。对称12相SPMSM正常运行时，各相绕组通正弦电流，第j相绕组电流如下所示：

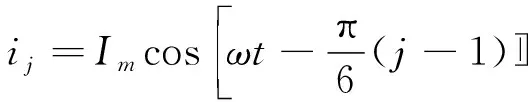
(21)

式中:Im为相电流幅值；j=1,2,3,…,12。

当电机任1相绕组断路缺相时，故障监测单元检测到该绕组的输出电流异常，控制板将封锁触发脉冲，该相绕组退出工作。为了保证12相SPMSM的正常工作，需要及时地调整剩余相电流的幅值和相位，才能够使旋转磁动势的幅值恒定，电流表达式如下所示：

(22)

式中:I′m为容错电流幅值；α为容错电流相位偏移角度。

图10给出了单相断路时，电磁输出转矩随电流幅值和各相容错电流角度变化的三维分布图。图11给出单相绕组故障断路时，电磁转矩脉动随电流幅值和各相容错电流角度变化的三维分布图，由图11可知，转矩脉动在6.0%～6.8%，当α=0.2 rad时，转矩脉动最小。

根据发生缺相故障前后，电机输出的平均转矩保持不变的原则，以最小相电流幅值为优化目标，得到了相等的相电流基波有效值，求得各相容错电流的解为I′m=13.2 A=1.1Im，α=0.18 rad。图12给出了基于解析法和有限元仿真计算得到的优化后的电磁转矩波形图，解析法和有限元仿真电磁转矩有效值分别为389.1 N·m和387.4 N·m，转矩脉动分别为6.0%和4.6%。

4 试验测试

为了进一步验证所提方法的正确性，对一台12相SPMSM进行试验测试。主要对电机进行了空载测试，并基于反拖法对样机的线空载反电动势进行了测试，样机如图13(a)所示。图13(b)为样机空载反电动势试验测试平台，试验过程中被测试电机通过联轴器与原动机直流电机相连接。图14给出了被测试电机的空载反电动势，试验过程中被测试电机通过联轴器与原动机直流电机相连接，测得第1相和第5相端部的线空载反电动势，其有效值为325.0 V，证明了本文所提解析模型的有效性。

为了进一步分析多相SPMSM负载特性，对驱动电机无故障状态下的额定工况进行了测试，图15给出了额定运行工况下的电流波形，示波器测试得到的相电流有效值为12.3 A。图16给出了测功机测试得到的输出转矩波形图，其输出转矩平均值为389.5 N·m，转矩脉动仅为1.6%，同前文的解析计算结果误差较小。同时由于试验条件有限，关于多相SPMSM的容错性能试验测试会在后期进行深入分析。

5 结 语

本文基于傅里叶级数分析方法，建立了多相SPMSM绕组缺相不对称运行下的磁场解析计算模型，并以一台44极48槽12相船舶用内转子SPMSM为例，进行了有限元仿真和试验测试，得到以下结论。

(1) 本文提出的解析计算模型能够对气隙磁密、空载反电动势、电磁输出转矩以及转矩脉动等性能参数进行准确计算，同有限元仿真计算结果相比，误差较小；

(2) 本文提出的解析计算模型能够实现对SPMSM绕组不对称运行下的电磁转矩以及转矩脉动等性能参数进行准确、快速计算，电磁转矩计算误差在2.0%以内；

(3) 对任1相绕组故障不对称运行下的容错性能进行分析，在电机输出的平均转矩保持不变的前提下，以最小相电流幅值为优化目标，转矩脉动增加到6.0%，对提高多相SPMSM驱动系统可靠性至关重要;

(4) 最后，对一台44极48槽12相SPMSM进行试验测试，同试验测试的线空载反电动势结果相比，有效值计算误差仅为3.2%；测试得到额定电流下输出转矩为389.5 N·m，计算误差较小，间接验证了本文所提绕组不对称运行下磁场解析建模的有效性。