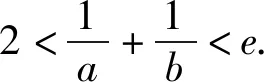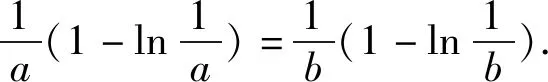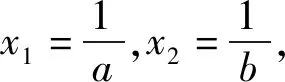合理构造函数 巧妙证不等式
龚小敏
(江苏省通州高级中学 226300)
构造函数法证明不等式,是指在利用导数法证明与函数有关的不等式时,根据所要证明的不等式,构造与之相关的函数,通过求导,利用函数的单调性、极值、最值等基本性质来加以证明.而在具体证明时,就要综合函数的不同确定形式,合理选择对应的函数,从不同思维视角来合理构建满足条件的函数解析式,进一步加以求导处理,巧妙证明.
1 作差构造法
证明譬如f(x)
例1已知函数f(x)=2ln(x+1)+sinx+1,求证:当x≥0时,f(x)≤3x+1.
分析利用所要证明的不等式进行作差处理,通过作差构造函数,借助求导来分析与确定函数的单调性,进而求出对应构建函数的最大值,通过不等式的确定以及变形与转化来证明相应的不等式.
证明设函数h(x)=f(x)-(3x+1)=2ln(x+1)+sinx-3x,x≥0,
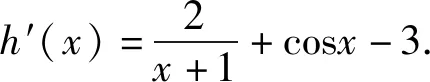
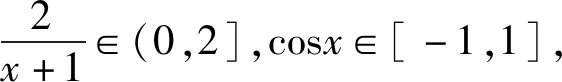
从而函数h(x)在区间[0,+∞)上单调递减.
所以h(x)=f(x)-(3x+1)≤h(0)=0,
即f(x)≤3x+1成立.
2 拆分构造法
对于一些所要证明的不等式中含有指数式或含有对数式,求导时不易直接求最值,可通过代数关系式的合理拆分变形来构造函数,利用函数的基本性质来证明对应的不等式;有时也合理拆分变形来构造两个函数,分别计算它们的最值,利用隔离分析最值来证明对应的不等式.
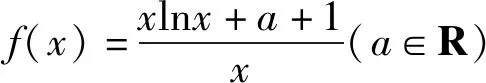
(1)求实数a的取值范围;
分析(1)通过函数求导,结合导函数的零点加以分类讨论,确定函数的单调性及极值的存在性,进而得以确定实数a的取值范围;(2)通过对所要证明的不等式加以分析,通过拆分构造法构造函数,通过函数的单调性及最值的确定来合理转化,进而加以证明相应的不等式.

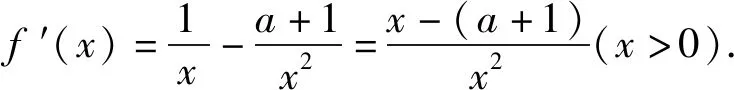
当a+1≤1,即a≤0时,在区间[1,2]上f′(x)≥0,所以函数f(x)在[1,2]上单调递增,无极值;
当a+1≥2,即a≥1时,在区间[1,2]上f′(x)≤0,所以函数f(x)在[1,2]上单调递减,无极值;
当1 综上分析,可得实数a的取值范围为(0,1). 只需证xf(x)>a(x+1). 只需证xlnx+a+1>ax+a. 即证xlnx>ax-1. 设函数g(x)=xlnx-ax+1, 则g′(x)=lnx+1-a. 所以函数f(x)在区间(0,ea-1)上单调递减,在区间(ea-1,+∞)上单调递增. 所以函数g(x)≥g(ea-1)=(a-1)ea-1-aea-1+1=1-ea-1. 因为0 则g(x)>0.即xlnx>ax-1. 对于所要证明的不等式中含有两个及以上参数的不等关系式,经常借助合理变形,整体化处理,进行合理换元构造对应的函数,化多参数为单一参数,进而通过函数的基本性质、不等式的性质等来分析对应的不等式证明问题. 分析结合满足题目条件的关系式的恒等变形转化,合理配方转化,换元构造对应的函数,结合函数的单调性与最值建立对应的不等式,结合二次不等式的求解来证明相应的不等式成立问题. 证明对于函数f(x)=lnx+x2+x(x>0), 由正实数x1,x2满足f(x1)+f(x2)+x1x2=0, 从而(x1+x2)2+(x1+x2)=x1x2-ln(x1x2). 令t=x1x2(t>0),函数φ(t)=t-lnt, 易知函数φ(t)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增.所以函数φ(t)≥φ(1)=1. 所以(x1+x2)2+(x1+x2)≥1. 在证明不等式时,结合相关所要证明的不等式所对应的关系式的合理转化或变形,提取出其中相同或相似的代数结构,寻找结构的同型或共性,进而合理同构相应的函数模型,结合导数以及函数的基本性质、不等式性质等来合理转化,巧妙证明. 例4(2021年数学新高考Ⅰ卷第22题)已知函数f(x)=x(1-lnx). (1)讨论f(x)的单调性; 分析(1)中首先求得导函数的解析式,结合导函数的取值符号即可确定函数的单调性;(2)中利用同构关系将原问题中不等式的证明转化为极值点偏移的问题,结合变形的关系式的特征同构相应的函数,利用函数的单调性与极值来证明对应的不等式问题. 解析(1)由函数的解析式可得 f′(x)=1-lnx-1=-lnx. 则当x∈(0,1)时,f′(x)>0,f(x)单调递增; 当x∈(1,+∞)时,f′(x)<0,f(x)单调递减. (2)由blna-alnb=a-b,得 不妨令x1∈(0,1),x2∈(1,e),则2-x1>1. 先证2 即证f(x2)=f(x1) 令函数h(x)=f(x)-f(2-x),x∈(0,1), 则h′(x)=f′(x)+f′(2-x)=-lnx-ln(2-x)=-ln[x(2-x)]在(0,1)单调递减. 所以h′(x)>h′(1)=0. 故函数h(x)在(0,1)单调递增. 所以h(x1) 即f(x1) 亦即2 再证明:x1+x2 要证x1+x2 同理,根据(1)中函数f(x)的单调性,即证f(x2)=f(x1)>f(e-x1). 同构函数φ(x)=f(x)-f(e-x),x∈(0,1), 则φ′(x)=-ln[x(e-x)], 令φ′(x0)=0, 则当x∈(0,x0)时,φ′(x)>0,φ(x)单调递增;当x∈(x0,1)时,φ′(x)<0,φ(x)单调递减. 又x>0,f(x)>0,且f(e)=0, 故x→0,φ(0)>0,φ(1)=f(1)-f(e-1)>0. 所以φ(x)>0恒成立. 即x1+x2 其实,构造函数法证明不等式时,除了借助以上一些常见的作差构造法、拆分构造法、换元构造法、同构函数法以及创新构造法等构造函数的基本方法外,还可以通过分类讨论、数形结合以及多个函数的构造等方法来证明相应的不等式成立.破解的关键是借助导数思维,抓住用导数判断函数单调性来处理对应函数的单调性、极值或最值问题,从而再转化为对应的不等式问题,达到有效证明不等式问题,全面提升导数的综合应用,提高数学能力,培养数学核心素养.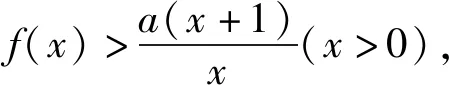
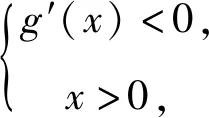
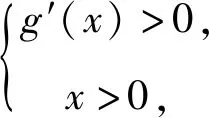

3 换元构造法
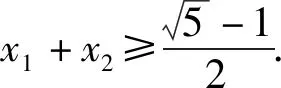
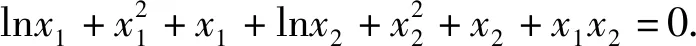
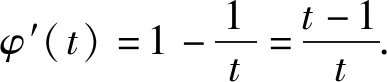
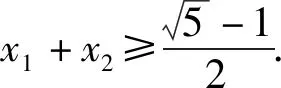
4 同构函数法