一道北京大学强基数学题的变式探究及推广
2022-11-03 04:13:44金迅婴
数理化解题研究 2022年28期
金迅婴 李 盛
(1.浙江省东阳中学 322100;2.浙江省杭州二中未来科技城学校 311121)
1 题目呈现
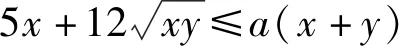
A.8 B.9 C.10 D.前三个答案都不对
这一试题从外部结构初看是含参不等式恒成立问题,但内涵丰富,隐藏着丰富的函数思想,具有一定的探究价值.
2 题目解析

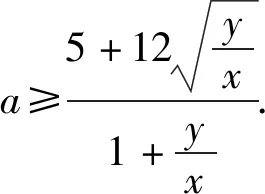
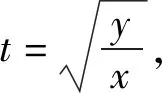
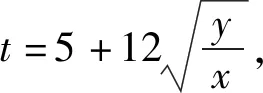
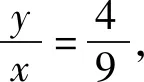
解法2比解法1简单,但不如下面的解法简捷.
解法3 (待定常数法)引入待定常数λ>0,根据基本不等式,得
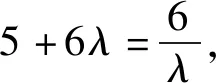


故a的最小值为9.选B.
解题过程十分简洁!但不是解决这类问题的一般性方法.一般方法是化生为熟的基本不等式法.
解法4由于题给不等式对任意正数x,y恒成立,利用极限方法,令y→0,得ax≥5x.
又x>0,所以a≥5.
将题给不等式变形,得

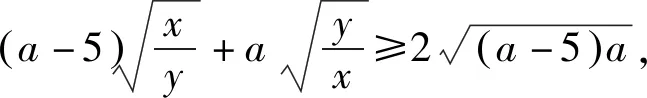
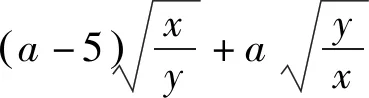
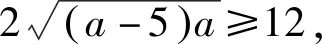
所以a的最小值为9.故选B.
评注解法4先采用极限方法,先确定实数a的一个范围, 再用分离法求解,是解决这类问题的一般方法.
3 变式探究
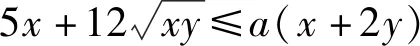

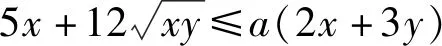
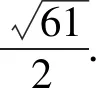
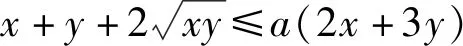
解析利用柯西不等式,得
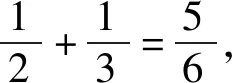
还有很多变式,不一一列举.
4 结论推广
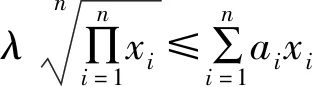
经研究,得
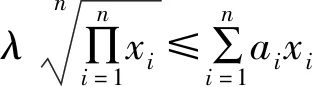
证明由于不等式①对任意正数xi(i=1,2,…,n)恒成立,采用极限方法,令xi→0(i=2,…,n),得a1x1≥0.
又x1>0,所以a1≥0.
同理可得:a2≥0,a3≥0,…,an≥0.
将不等式①变形,问题转化为:
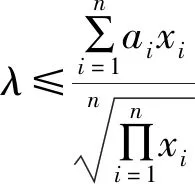
应用n元的算术——几何平均值不等式,可得
且等号在a1x1=a2x2=…=anxn时成立.
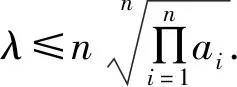
这样一来,用同一方法,就把问题推广到了n元加权的算术——几何平均值不等式有关的恒成立问题.
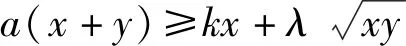
解析已知不等式可化为
由定理,知应满足的条件为.
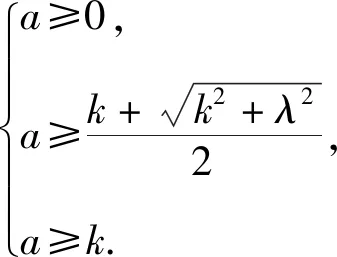
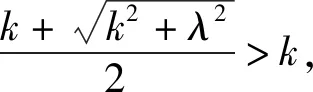

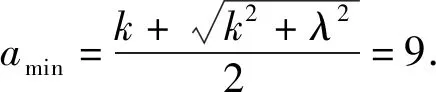
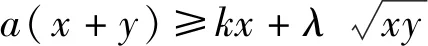
猜你喜欢
数学年刊A辑(中文版)(2021年1期)2021-06-09 09:32:06
中学生数理化·七年级数学人教版(2019年9期)2019-11-25 07:34:34
小天使·二年级语数英综合(2017年9期)2017-10-20 21:09:35
小雪花·小学生快乐作文(2016年12期)2017-03-08 00:50:58
中学生数理化·七年级数学人教版(2016年9期)2016-12-07 08:28:52
中学生数理化·七年级数学人教版(2016年8期)2016-12-07 07:25:19
山西大同大学学报(自然科学版)(2016年4期)2016-11-27 02:20:55
新高考·高一物理(2016年3期)2016-05-18 16:16:56
小天使·一年级语数英综合(2016年5期)2016-05-14 23:32:12
读写算(中)(2015年12期)2015-11-07 07:25:01

