基于粒子群优化算法的搬运机器人标定方法研究

刘海龙, 李移伦, 吴海波

(湖南铁道职业技术学院，湖南 株洲 412001)

0 引 言

现有串联型工业机器人在无工具或简单规则工具的情况下，可采用直接测量得出数据并输入的方式完成标定。但在视觉与力觉反馈的工业机器人上下料系统中，由于工业机器人的法兰盘前端带了复杂且不规则的上下料工具，因此无法直接测量和标定，现有的方法一般是利用机器人的结构关节参数计算间接获得，在精度上无法保证，可以说机器人末端的姿态精度极大取决于关节的标定精度[1-2]。工业机器人机构参数的高精度标定问题，是机器人现场应用及精确定位的基础和首要解决问题，也是机器人领域研究的重点问题之一。

近年来，随着粒子群优化算法(particle swarm optimization,PSO)研究的不断深入，在工业机器人运动学和轨迹设计等领域也有较多的应用研究[3-4]。尤其是量子粒子群优化算法(quantum-behaved particle swarm optimization,QPSO),能够更好地适用于工业机器人运动学中复杂工具多参数多组合等问题的优化场合，具有更好的全局应用能力[5]。房立金等[6]利用PSO算法实现对并联工业机器人驱动杆参数进行优化设计，能够有效修正设计轨迹与理想轨迹的偏差。黄进等[7]提出一种基于PSO算法对机器人外第七轴运行参数进行优化的方法，并试验证明能有效提高机器人与外第七轴的整体协调运动精度。Couceir等[8]QPSO算法应用于多工业机器人协同作业的防碰撞系统，并取得较好的防碰撞效果。Juang等[9]提出基于神经网络与QPSO结合的机器人动力学标定方法，并实际应用于超精密六自由度串联工业机器人中，取得较好的精度效果。本文在此基础上，提出一种符合串联工业机器人搬运系统标定的粒子群算法，可以实现对串联工业机器人进行运动学分析，建立相应的误差模型，将运动学标定问题转化为非线性的优化问题，实现对串联工业机器人机构的参数标定。

1 工业机器人机构参数的标定

在工业机器人上下料系统中采用的是串联型六轴搬运工业机器人，本文利用串联机器人的正运动学方程来建立对应的标定模型进行求解分析，其标定的方法流程如图1所示。首先利用运动学方程建立机器人的姿态误差模型，再根据测量和现场工况需求选择合适的机构参数，根据前面所建立的模型计算出对应的末端姿态数据，应用粒子群优化算法进行最优化寻优求解得到最佳的结构修正量，作为串联机器人运动学标定的结果[10-11]。

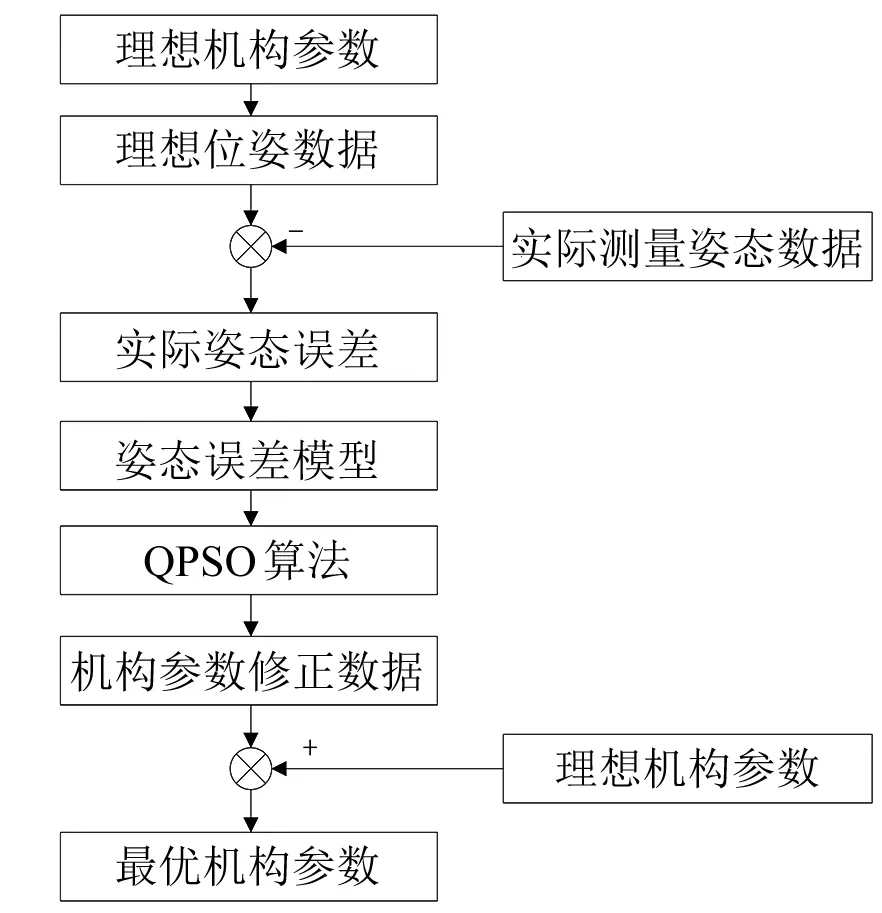
图1 串联型工业机器人结构参数标定方法

2 串联型工业机器人姿态误差模型

选用ABB IRB4400六轴串联机器人为研究对象，其基本结构如图2所示，硬件设备机构主要包括基座、六个关节轴和末端法兰盘装置等，坐标系和坐标系分别表示基座固定平台和机器人法兰盘末端坐标系[12-13]。

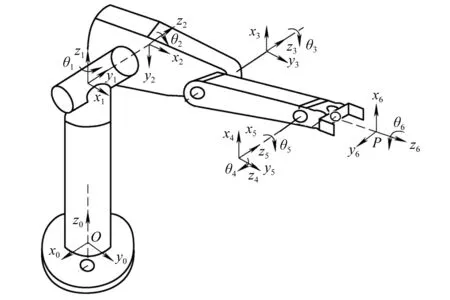
图2 IRB4400六轴串联机器人机构图

利用DH矩阵法，建立了IRB4400六轴串联机器人的运动学方程：

TOP=T1,T2,…，Tv，…，T6

(1)

Tv=rot(z,θv)trans(0,0,dv)trans(lv,0,0)rot(x,av)

(2)

式中:TOP为P坐标系相对于O坐标系的位置变换矩阵；Tv为v坐标系相对于v-1坐标系的位置变换矩阵；θv为第v个关节的轴转动角度；dv为第v个关节的关节距离；lv为第v个关节的连接杆件长度；av为第v个关节的连接杆件扭转力矩。

对以上公式进行微分处理及整理可得到处理串联工业机器人的误差模型，结果为：

δP=Fs(δθv,δdv,δlv,δav)

(3)

式中:δP为串联机器人末端姿态误差。

3 粒子群优化算法标定问题求解

3.1 优化变量设计

应用粒子群优化算法的目的是将标定过程中的标定问题转成非线性的最优化求解问题，再进行求解[14]。由前面的运动学方程式和误差模型可以得到，调整机器人误差模型中的参数可以改变机器人的末端姿态，这些参数正是机器人运动中的各类误差源，将这些误差源记为Δq，表示相应机构参数的纠正量，利用粒子群优化算法寻找最优解。因此Δq所表示的机构参数修正量则为最优化求解方向，对于粒子群优化算法，每个粒子则表达一组机器人机构参数的最优解，对于串联型工业机器人及运动学方程和模型可以得到如下计算式。

Xi(t)=Δq=[δθv,δdv,δlv,δav]

(4)

式中:Xi(t)为一组粒子群优化最优解位置矢量；Δq为机构参数修正量。

3.2 目标函数设计

根据前面的推算分析，以串联工业机器人姿态误差模型为基础，根据法兰盘末端的姿态精度要求，针对非线性问题设计最优化的目标函数方案：

(5)

式中:Q为求得的目标函数值；F(Δq)为串联工业机器人姿态误差函数，变量为δ，在目标函数中，引入Δq作为变量；k为放大系数，根据姿态位置精度要求确定；e为实际得到的姿态位置误差。

根据式(5)的推算，可以计算出第i个粒子下的姿态误差，该误差是由机构参数修正量Δq所引起，再利用F(Δq)函数与实际得到的姿态位置误差e求得目标值Q,当仿真求得的误差目标结果Q>1时，说明收敛结果超出目标精度要求，没有满足设计目标，需要调整变量Δq的数值，当误差目标结果Q≤1时，说明结果满足目标精度要求。

3.3 粒子群优化算法

在量子粒子群优化算法计算之前需要先设定粒子数为N，迭代次数为t，最大的迭代次数为tmax，采用粒子群优化算法进行标定问题。首先在串联型工业机器人的工作内容中取μ组姿态工况，测量得到实际姿态数据H，通过前述的内容可以推算出实际的姿态误差eh，其中h为每次姿态工况的对应的数据，最大为μ。随后对粒子群参数进行初始设置，将N个粒子群的初始位置均设置为Xi(0)，粒子群的维数M配置成与机构参数的纠正量Δq的维数一致，确定粒子群的全局最优位置，如式(6)所示。

Pg(0)=min{X1(0),X2(0),…，XN(0)}

(6)

式中：Xi(0)为第i个粒子群的初始位置,i=1, …，N。

通过上式(6)计算粒子的适应度，将第i个粒子的位置数据Xi(t)引入，分别计算μ组测量构型下该粒子的目标函数值Q，然后求取平均值，从而求得将第i个粒子的适应度数据，如式(7)所示。

(7)

式中:μ为测量构型的数组数量。

式(7)的计算表示为:第i个粒子的位置数据Xi(t)作为变量，引入误差模型后产生的姿态误差与实际姿态误差进行比较。以粒子群适应度最小化为优化目标，通过式(7)得到一系列数据组，表示与实际姿态误差eh对应的最优机构参数修正数据Δq，进而推算出最优机构参数q，该参数值与测量得到实际姿态数据H相对应。通过对μ组姿态工况的计算，可以实现更新粒子群全局最优解，该最优解既是标定问题的最优解，如式(8)所示。

(8)

式中：Pg(t)为粒子群全局最优解。

当机器人的运动精度达到要求时，即满足迭代算法终止条件，此时的粒子群最优解Pg(t)则是串联机器人的标定最优机构修正数据Δq，进而推算出最优机构参数q，若未满足迭代终止条件时，则返回继续运算，直至运算结束。

4 串联机器人上下料系统试验分析

根据机器人法兰盘及上下料定位需求约束机构的结构特征和三维空间运动的特性，将空间约束、工装夹具以及工作台综合简化为七轴串联联动机构。如果某个轴的转动轴线平行误差较大，将会影响到约束机构的运动自由度三维空间，因此前六轴的运动控制和标定需要有较高的精度水平，否则直接影响第七轴的自由约束空间。空间约束机构内的几何误差源主要包括工业机器人的六轴姿态误差以及工装夹具的尺寸误差。将工业机器人上下料工作站的七轴空间约束的主要误差源经过分析，转化为机构参数的修正量Δq，如表1所示。上下料工作站的姿态误差由工业机器人工件坐标系下的三维空间X轴、Y轴和Z轴表示，机器人工装夹具的尺寸修正量为供机器人工具坐标系的三维空间X、Y、Z轴表示。

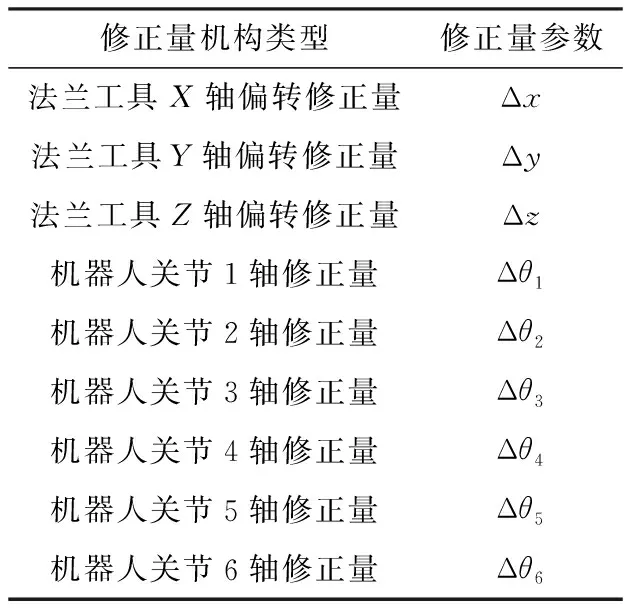
表1 约束机构参数修正量

针对六轴串联型工业机器人约束机构进行运动学标定的试验中，需要对机器人前端法兰安装的工具机构进行X轴偏转、Y轴偏转和Z轴偏转姿态进行误差补偿，并以机器人的六个关节轴的精度要求建立法兰X轴方向上的优化目标函数，对约束机构部分的参数进行运动学标定。可以得到优化变量表达式为：

(9)

以X轴方向上的精度要求为优化目标，可得到目标函数为：

Q=f(Δy,Δz,Δθκ)=Kx|dx|

(10)

式中:Kx为X轴方向上的放大系数。

目标函数建立完成后，对法兰工具X轴偏转姿态误差进行测量，分别测试Z轴为300 mm和450 mm处不同Y轴、X轴的姿态误差，一共测试了5组共25种不同姿态的参数。通过测量结果计算出平均测量误差为0.563 mm，最大误差为0.624 mm，最小误差为0.512 mm，可以看出在Y轴和Z轴同时偏移增大的情况下实际误差也呈增大的趋势。详细数据如表2所示。

表2 轴姿态误差测量结果 单位：mm

利用粒子群优化算法对上述变量进行最优计算，选取30、60、90个粒子群组进行迭代计算，最大迭代次数为200，直到计算结果收敛并且稳定。计算得到QPSO算法的收敛效果好，当粒子数逐步增大时，最小适应度也从0.356减小到0.332，虽提高了标定精度，但是效率会存在一定的降低。由于精度提高较小，因此粒子数需要综合效果平衡的结果，选择粒子数N=60时得到最优的机构参数修正量结果。将该结果引入已建立的模型中，得到优化后的X轴姿态误差，详细数据如表3所示。

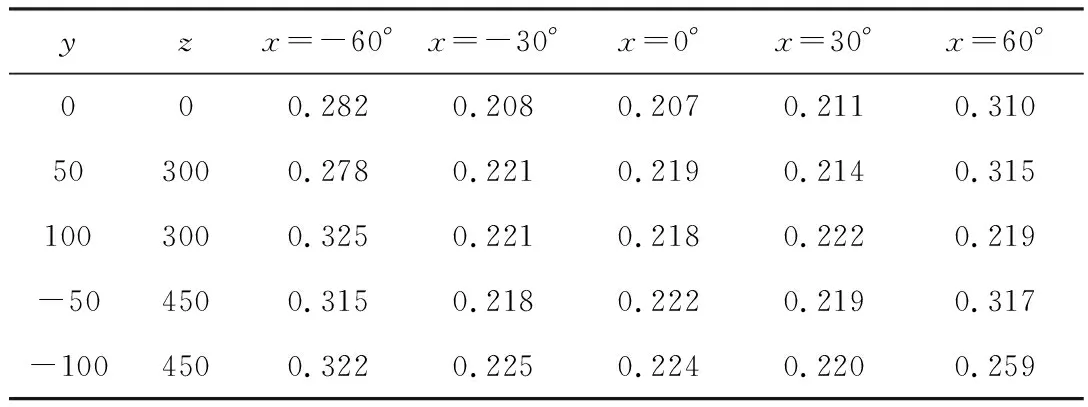
表3 优化后轴姿态误差测量结果 单位：mm

由表3优化后的测量结果可得，引入优化后修正量的轴姿态平均误差为0.248 mm，最大误差为0.322 mm，最小误差为0.207 mm，经过QPSO算法优化后的机构修正参数得到的轴姿态误差精度大幅度提高。

5 结束语

针对串联型工业机器人进行误差建模分析及标定方法，基于QPSO算法提出一种应用于串联型搬运机器人的的标定方法。该方法针对带异形搬运工具的搬运工业机器人进行优化，实现机器人六轴关节及外第七轴关节参数求得最佳约束机构参数修正量。本文利用量子粒子群算法全局优化能力实现对非线性运动模型进行优化，将复杂的非线性标定问题简单化，并以六轴串联机器人上下料系统为案例进行验证测试。通过试验表明，该方法应用在机器人六轴关节及外第七轴关节的标定中误差精度得到大幅度提高，平均误差和最大误差分别减小55.8%和48.4%以上。