改进的NSGA2算法在航空活塞发动机装配中的应用
李春林,庞晓平,张 果
(重庆大学 机械工程学院,重庆 400044)
航空发动机的诸多性能与航空发动机的装配质量,装配效率密切相关[1]。装配是发动机制造过程中最为重要的环节之一[2],航空发动机装配成本占发动机成本的40%,装配工作量占整体工作量的50%[3]。选择装配法能够在零部件按照经济精度加工时,仍然可以获得较高的装配精度,因此成为航空发动机等精密复杂机械的常用装配方法。所谓选择装配是指通过检测和挑选待装零配件,有选择性地进行装配,以达到较高装配精度的一种装配方法。在航空发动机等一些高精度装配体上,存在多个需要同时保证的装配功能要求,称为多质量要求[4]。因此,航空发动机选择装配往往是一个多目标优化问题,与单目标优化结果不同的是多目标优化希望获得的是一组丰富度高,分布均匀的解。
第二代带精英保留策略的NSGA2(non-dominated sorting genetic algorithm2) 快速非支配排序算法,基于拥挤距离的分布性方法和精英保留策略,凭借简单、高效等优点,在多目标优化领域中得到广泛的应用。张守京等[5]提出基于拥挤度的自适应交叉算子,引进竞争选择机制,保证解集的多样性;Bin等[6]采用自适应交叉和变异的方法,提高了算法的收敛速度和搜索能力;Xu等[7]采用正交设计和累积排序策略改进了NSGA2算法,并以尾灯支架装配为例,证明改进的NSGA2算法具有明显的优化效果;Baviskar等[8]提出两种基于渐进式步长机制的算法,并与现有非支配排序遗传算法的搜索方式相结合,通过控制步长和分割数目,在下一代中产生更好的染色体,实现快速收敛。张晓娟[9]提出一种链式智能体遗传算法CAGA(chainlike agents genetic algorithm),通过引入动态邻域竞争、邻域正交交叉、自适应变异等提高了算法的收敛速度。
以上研究在一定程度上改善了NSGA2算法的优化性能,但依然存在一些不足。在航空活塞发动机活塞与缸体的选择装配过程中,由于部分零部件的尺寸数据一致,必然存在相同的选配结果。相同个体经基因重组后不会改变基因结构,从而产生大量的重复个体。笔者针对NSGA2算法的精英保留策略无法抑制个体大量重复,造成解集多样性降低这一缺陷,提出一种基于拥挤度与种群丰富度相结合的子代精英保留策略。在零件装配中,由于零件尺寸不能更改的限制,本文提出仅在邻域圆环上的近邻搜索方式,提高了非支配解集的收敛性能,探究出一种适合航空活塞发动机选择装配的NSGA2算法。
1 目标函数
1.1 装配合格数
假设有一批零部件进行装配,装配完毕之后有n组零部件装配合格,则装配合格数为n。
1.2 装配精度
零件的装配精度以田口质量损失来度量,装配的质量损失常采用具有望目特性的田口质量损失模型,具有望目特性的田口质量损失模型可以保证配对公差是否落在设计公差带以内,对于满足设计公差的配对,理论上越靠近理想配合值的配对拥有更好的稳定性,对产品造成的质量损失也会最小[10-12]。田口质量损失模型如下:
(1)
式中:T示公差带宽度,y表示实际配合公差,o表示最佳配合值,λ∈[0,1]表示配合值处于设计公差带边缘的可接受程度,[o-αT,o+βT]表示设计公差带的范围。
在某航空活塞发动机中,设计要求缸体与活塞间隙范围为0.11~0.13 mm,取中间值0.12 mm为最佳配合o值,则α=β=0.5,公差带宽度T为0.02 mm,λ取1。在本文中以装配合格的零部件的平均质量损失来表征装配精度。
1.3 优化模型
在航空活塞发动机装配中,只需考虑装配合格部分的平均装配精度q1(X):
(2)
式中:X表示一批零部件的某一选配组合,N表示参与装配的零件组数,n表示装配合格的零件组数。因此q1(X)越小,X的装配精度越高。由式(1)(2)以及装配合格数n建立多目标化模型:
minF(X)=min[n(X),q1(X)],
(3)
其中,X∈Ω,Ω表示解空间。
2 优化算法
2.1 NSGA2算法
NSGA2算法基于非支配排序[13-14]将种群个体进行分层,对每层个体进行适应度分配,第一支配层级的适应度最高,然后依次降低,从而保证下一子代的优良性,提高算法进化效率。同时,采用外部存档机制的精英保留策略,结合拥挤度和支配层级筛选个体,具有良好的收敛性,得到的非支配解集分布也较为均匀。算法操作细节如下:
1)构造初始种群S0,设置算法控制参数(交叉概率Pc,变异概率Pm,最大进化代数g1,初始进化代数g=0,初始种群个体数目L),清空外部存档种群S1。
2)计算初始种群每个个体的装配合格率η和装配合格个体平均质量损失q,利用Pareto支配原理进行分层。
3)对每层个体赋予适应度值P(i),非支配层级高的适应度大,低的适应度小。
4)根据适应度值选择个体,对选择的个体进行交叉和变异,再次计算每个个体的装配合格数n和装配合格个体平均质量损失q,利用Pareto支配原理进行分层F1,F2,…,Fm。基于个体的支配层级和拥挤度选择个体。
5)将筛选出的个体存入外部种群S1,作为下一代亲代继续进化。
6)判断是否达到最大进化代数g1,如果没有,返回第(2)步,如果达到最大进化代数,则输出种群中最高支配层级F1的所有相异个体。

图1 NSGA2算法流程图Fig. 1 Flow chart of NSGA2 algorithm
2.2 NSGA2算法的改进及应用
2.2.1 构造适应度分配函数
适应度函数构造的基本准则是非支配层级高的个体适应度大,被选中的概率高,所有非支配层级的适应度值的和为1。因此以某一大于1的正整数a为底,非支配层级i为指数的指数函数来构造适应度函数P(i)。
(4)
式中m表示种群总层级数。由公式(4)可知,a越大非支配层级高的个体被选中的概率就越高,算法进化速度就越快,但是不利于种群多样性的维护,算法易陷入局部收敛,因此a的取值不宜过大。当初始种群规模为50时,a取不同的值非支配解集中相异个体的数量如表1所示。

表1 a的取值对非支配解集中相异个体数量的影响
因此存在个体重复现象且重复个体处于较高支配层级时,a的取值应尽可能小,这里取a=2。
2.2.2 改进子代精英保留策略
NSGA2的精英保留策略如图2所示。
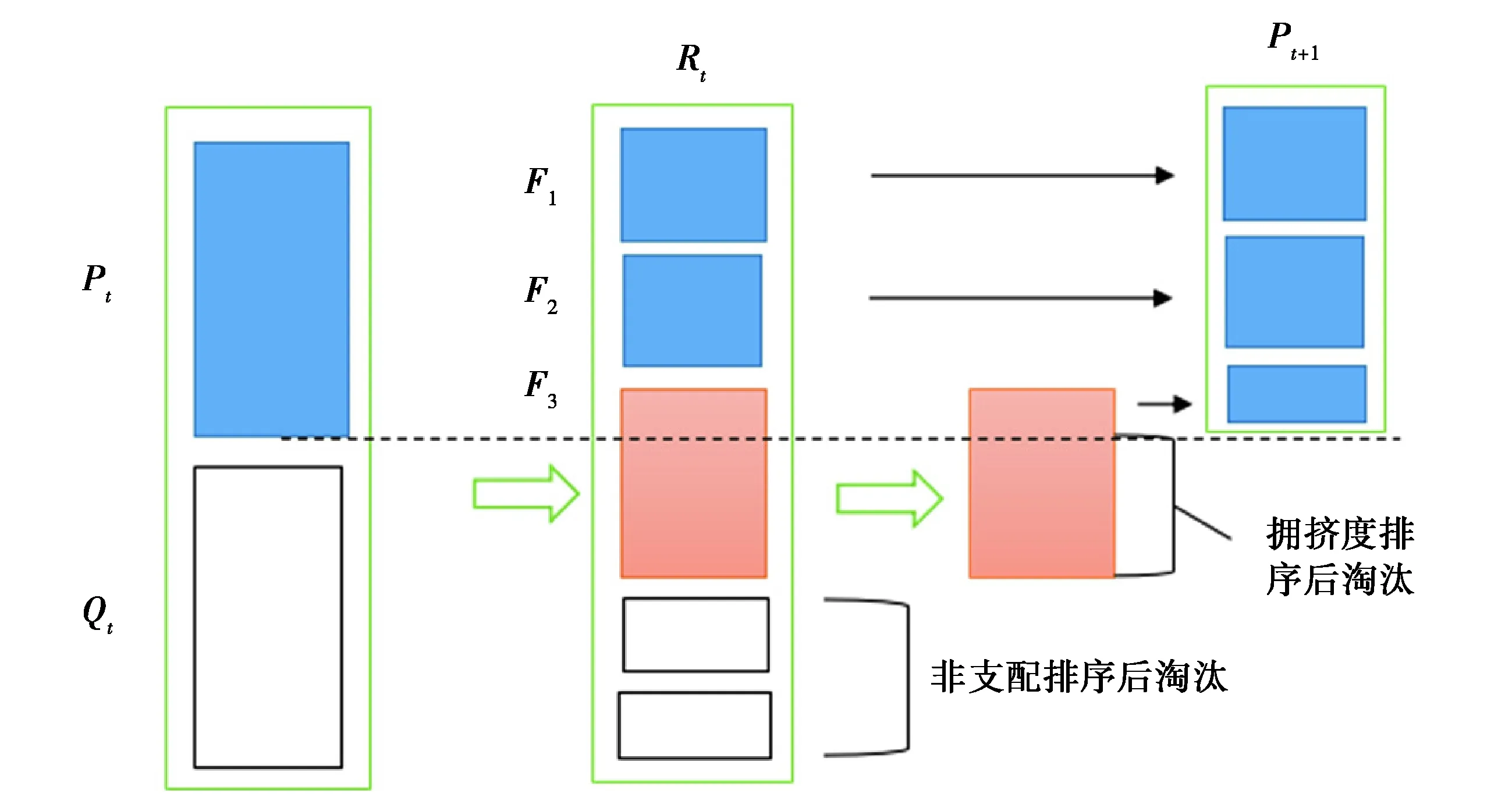
图2 NSGA2 子代产生原理Fig. 2 Principle of NSGA2 generation
如图2所示,将亲代Pt与子代Qt合并得到Rt,应用Pareto支配原理将Rt中的个体分为m层,即F1,F2,…,Fm,每层包含的个体数量为n1,n2,…,nm,显然有n1+n2+…+nm=N,其中N表示Rt中的所有个体的数量。由于支配层级高,处于第一和第二支配层级的所有个体F1,F2全部存入外部存档种群Pt+1,然后再在第三支配层中利用拥挤度比较选出N/2-n1-n2个个体加入外部存档种群,其中N/2表示外部存档种群Pt+1的数量。
下面给出NSGA2精英保留策略中常用的两个基本定义。
定义1(个体拥挤度)为了测算某点附近其他个体的聚集程度,定义变量idistance(拥挤度),表示覆盖个体i但不覆盖其他点的矩形面积,而同一支配层级首尾两端个体的拥挤度定义为无穷大。如图3[9]所示。
定义2(拥挤度比较算子)拥挤度比较算子,用于搜寻分布均匀的个体,两个体i和j的比较逻辑如下[9]。
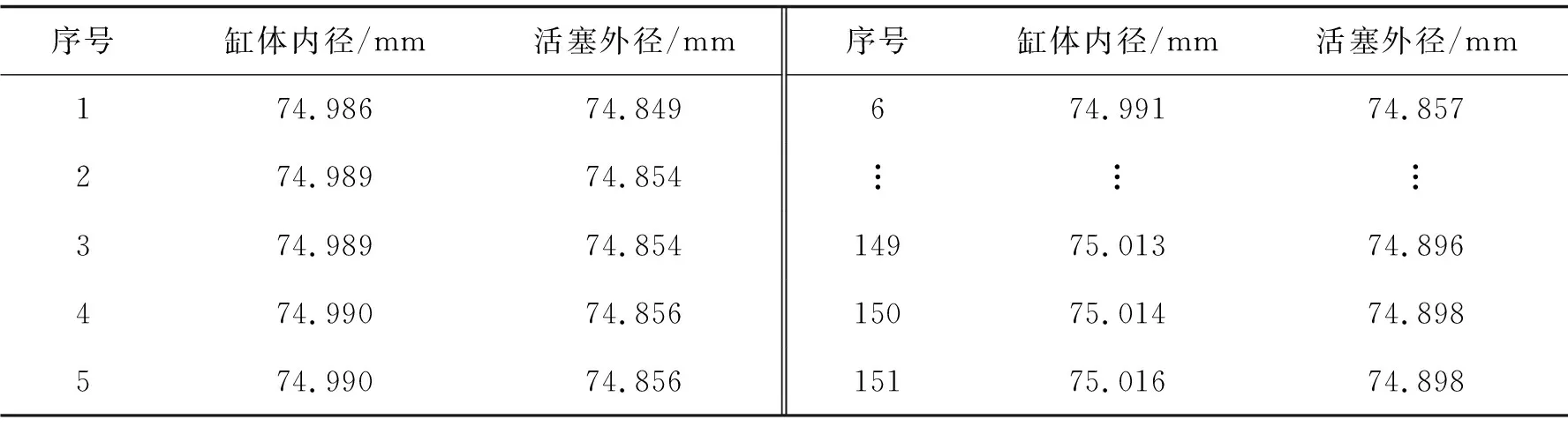
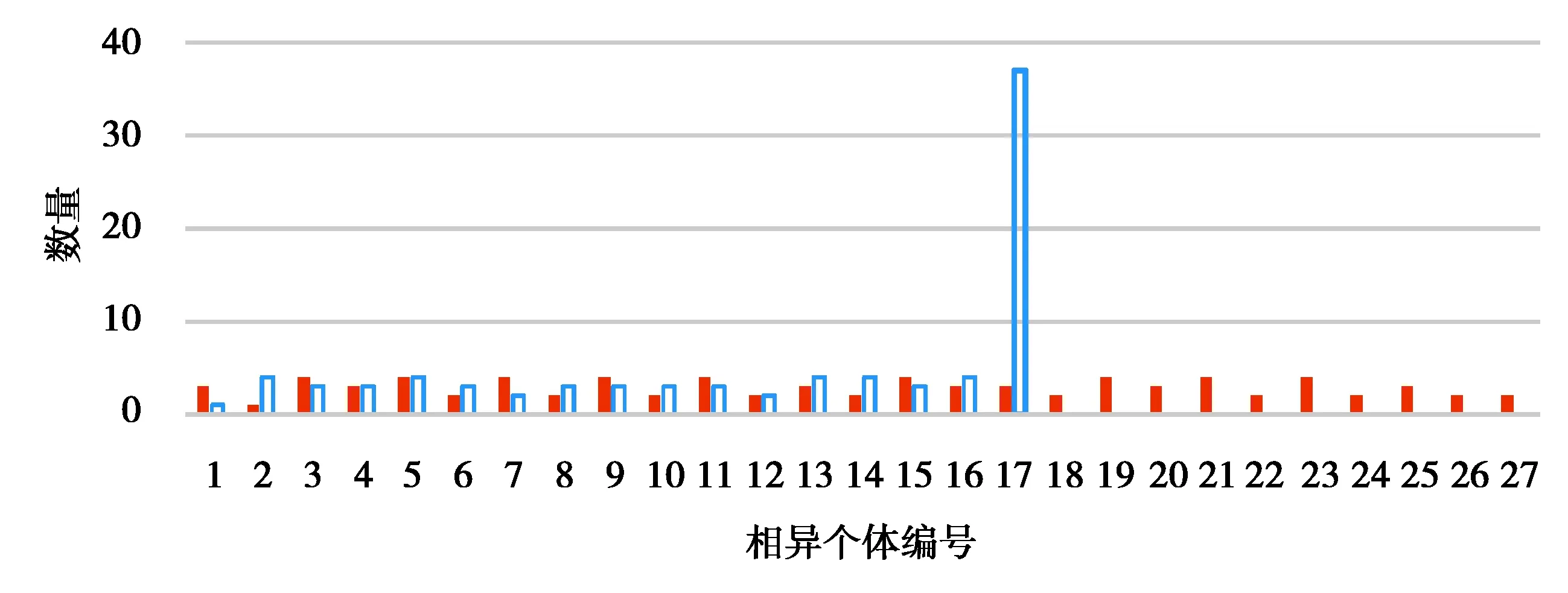
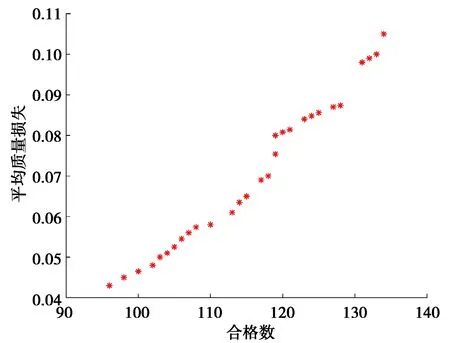
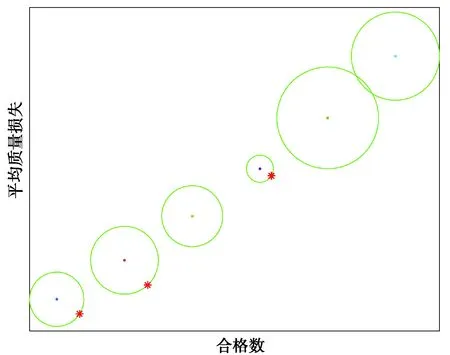
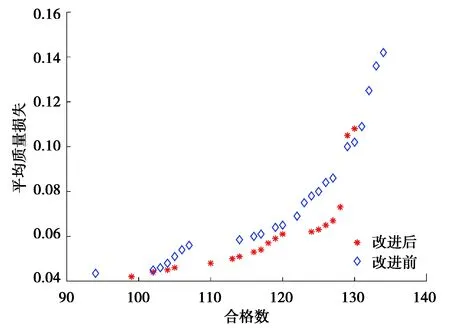
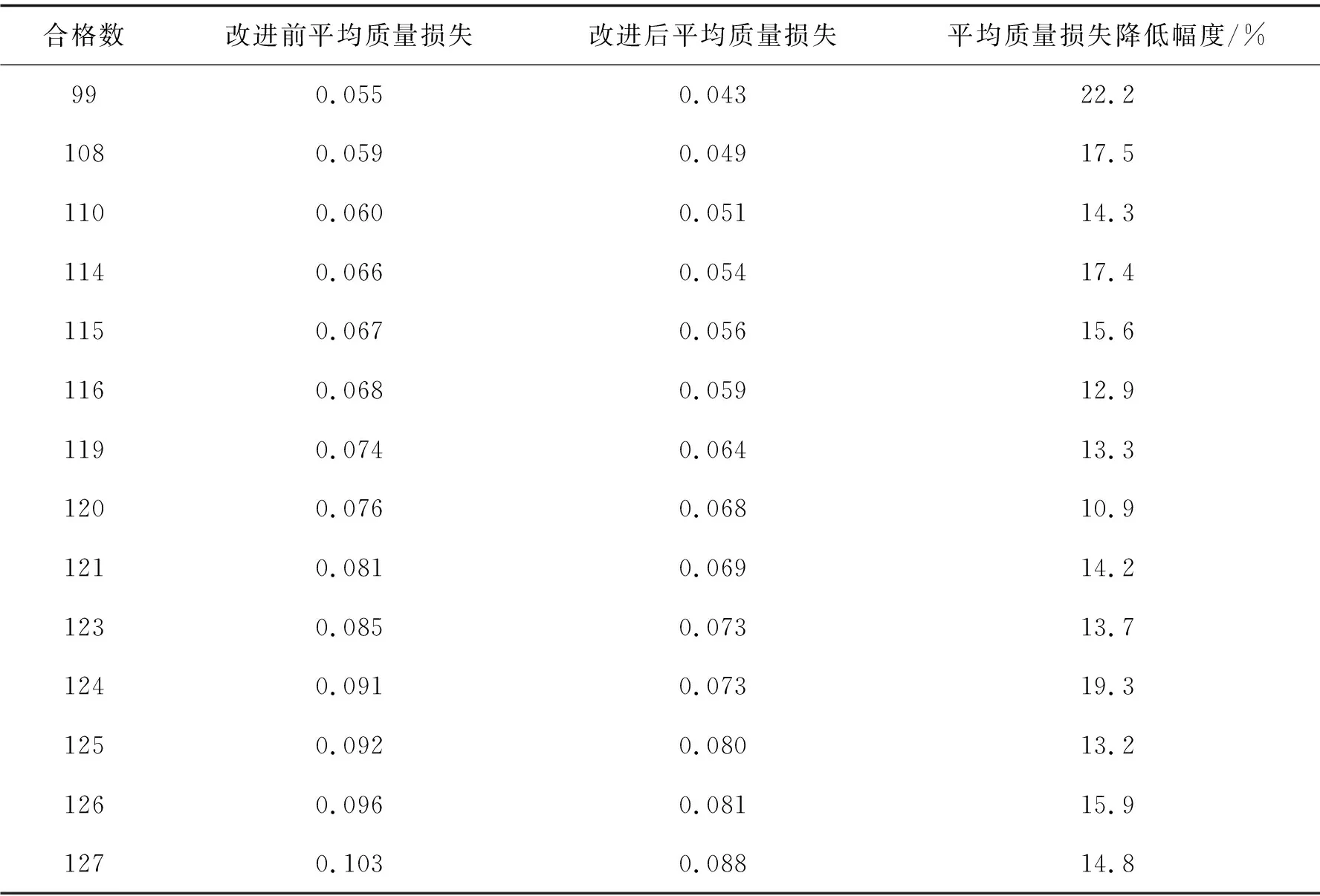
i (5) 式中irank表示个体i的非支配等级。 图3 拥挤度原理Fig. 3 Principle of crowding degree 由图3可知,计算拥挤度时非支配解集是以第一目标值f1按升序进行排列,因此当两个非支配解的拥挤度相等时会优先选择第一目标值大的个体,这就导致种群中第一目标值较大的个体数量过多。随着迭代的进行,非支配解集在第一目标值较小的部分逐渐缺失,不能完整地填充整个解空间。而基于种群均匀度和拥挤度相结合的子代精英保留策略则能够弥补这一缺陷。 以种群均匀度和拥挤度相结合的子代精英保留策略如图4所示。 图4 改进后的NSGA2 算法子代精英保留Fig. 4 Improved NSGA2 algorithm for elite preservation 2.2.3 解集评价指标 采用多目标优化结果常见的评价指标:解集收敛性测度、丰富度测度,以及本文中提出的种群均匀度。 1)收敛性测度。设X1,X2为2种算法获得的非支配解集,则收敛度计算公式为[15]: (6) 式中|.|表示集合中的元素个数,x1≥x2表示个体x1支配x2。如果C(X1,X2)=1,则表示X2中的个体均被X1所支配,反之,如果C(X1,X2)=0,则表示X2中的个体均不被X1所支配。同样的方法计算C(X2,X1),如果C(X1,X2)>C(X2,X1),则表明X1在种群收敛性测度方面优于X2。 2)丰富度测度。种群的丰富度测度以种群中相异个体的数量m表示。 3)种群均匀度。由于在种群中某一个体的大量存在,相异个体数量分布不均,导致种群丰富度降低,目前的评价指标中忽略了这一影响,这里提出种群均匀度的概念可以抑制这一影响,提高种群丰富度。具体定义如下: 假设一个种群有N个个体,其中相异个体有m个,它们的数量分别为n1,n2,…,nm,有n1+n2+…+nm=N,则种群均匀度H的定义为 (7) 式中n0=(n1+n2+…+nm)/m,可见当种群内的个体都是相异个体时,种群均匀度H最大为1,相同个体数量分布越不均匀,种群均匀度就越低。 以某型号航空活塞发动机缸体与活塞的装配为例,发动机缸体与活塞的装配间隙是极为重要的技术参数,装配间隙对发动机整机装配尺寸和装配质量影响很大,间隙的合格范围是0.11~0.13 mm,因此缸体内径与活塞外径尺寸精度也比较高,将151组缸体与活塞的尺寸数据按照升序排序如表2所示。 表2 缸体与活塞尺寸数据 缸体与活塞的配合为孔轴配合,封闭环即配合间隙为缸体内径与活塞外径的差值。为了更好地检验改进的子代精英保留策略对输出结果的影响,需要排除遗传算法交叉、变异环节的随机性,将改进前后的算法设立为并行的方式。采用直接编码的方式,以序号和对应的尺寸组成一个不可分割的基因位,将151组数据随机排列构成一个染色体,染色体的每一列表示一组缸体与活塞的装配,如表3所示。 表3 染色体结构 重复随机排列50次,得到初始种群S1,即初始种群的个体数是50,每个染色体表示一种选择装配方式。复制该初始种群,得到与S1完全相同的初始种群S2。将S1和S2在同一随机序列下进行交叉和变异,在同一分层机制下分层。子代精英保留方面,S1采用原始算法的子代精英保留策略,S2在此基础之上结合种群均匀度最大策略选择个体。 2个种群在相同的算法控制参数下运行,得到的非支配解集分布如图5所示。 图5 改进前后非支配解集分布对比Fig. 5 Comparison of non-dominated solution set distribution before and after improvement 星号点表示S2得到的非支配解集,菱形点表示S1得到的非支配解集。S1的非支配解集中非支配解有86个,S2有79个。S2非支配解集中相异个体有27个,S1仅仅只有17个,对2个解集的相异非支配解进行编号,统计各自数量,如图6所示。 图6 两组非支配解集相异个体数量分布对比Fig. 6 Comparison of the number distribution of different individuals in two groups of non-dominated solution sets 图中空心柱表示S1非支配解集相异个体数量分布,实心柱S2表示非支配解集相异个体数量分布。可以看出S2的非支配解集中个相异个体数量分布更加均匀,没有出现某一个体大量重复的情况。 将两组非支配解集进行收敛性测度、丰富度测度和种群均匀度检验,令S2的非支配解集为X2,S1的非支配解集为X1,计算结果如表4所示。 表4 非支配解集性能比较 由表4可知:C(X1,X2)>C(X2,X1),表明引进种群丰富度之后得到的非支配解集在收敛性测度方面并没有得到提高。这是因为在计算个体拥挤度时,首先以第一子目标(合格数)升序排列,当两个体拥挤度相等时,合格数较大个体更容易保留下来,因而导致合格数较大的非支配个体在种群中大量存在,在后续的变异中有更大的概率获得更加优异的非支配解。在丰富度测度方面和均匀度方面有:m(X1) 结合2组非支配解集,找出所有的非支配解,如图7所示。 图7 两组非支配解集合并后非支配解分布Fig. 7 Distribution of non-dominated solutions after merging two sets of non-dominated solutions 针对引进种群均匀度的精英保留策略会降低非支配解集收敛性,导致算法进化速度减慢这一缺陷,引进近邻搜索算子。近邻搜索能够提高多目标优化遗传算法的收敛速度,弥补引进种群均匀度后非支配解集收敛性测度降低的不足。所谓近邻搜索指的是在某一范围内算法往某一特定的方向进化[16]。文献[16]提出的近邻搜索是在整个近邻圆内进行邻域搜索,如图8所示。 图8中圆心点表示经交叉变异后获得的非支配解,星号点表示在圆心点附近的最优解,由于NSGA2的交叉变异环节具有随机性,局部搜索能力不足,很难得到最优解。 在整个近邻圆内的邻域搜索范围表达式如下[16]: R=X±ρ。 (8) 由于染色体的基因位是由零件尺寸和序号组成,是一一对应关系,不能更改。为了满足这一约束条件,重新定义搜索半径和搜索范围。任意交换2对基因位,交换之后的染色体与之前的染色体的欧式距离定义为搜索半径ρ1。 若个体X1=(x1,x2,x3,x4,…,xn)交换两对基因位之后变为X2=(x2,x1,x4,x3,…,xn),则对X1局部搜索的搜索半径ρ1表示为: (9) 因此,每个非支配解的搜索半径是不相等的,若对m个非支配解进行近邻搜索,搜索半径向量为: ρ=(ρ1,ρ2,…ρm), (10) 则搜索范围表示为: R=X+ρ。 (11) 近邻搜索的示意图如图9所示。 图8 在整个近邻圆内进行邻域搜索Fig. 8 Neighborhood search in the whole neighborhood circle 图9 在圆环上进行邻域搜索Fig. 9 Neighborhood search on a ring 圆心表示原始非支配解,星号点表示更优异的非支配解。可以看出近邻搜索并非是在整个邻域范围内进行搜索,由于零件尺寸不能更改的限制,邻域搜索只是在以非支配点为圆心,搜索半径为圆的圆环上进行,每个点的搜索半径由于交换基因位的随机性是不相等的。 显然,若只对一个点进行近邻搜索是很难得到更优的非支配解,但是同时对所有的非支配解进行邻域搜索,随着迭代的进行,搜索到最优的非支配解的概率会大幅提升。与标准的NSGA2多目标遗传算法不同之处在于,引进了近邻搜索后,算法对每次进化得到外部存档种群中所有个体进行近邻搜索,若在搜索圆环上存在更优异的非支配解,即X2≥X1,那么就用X2替换X1。为了排除交叉变异环节的随机性,采取程序并行的方式,2个相同的初始种群S1和S2在相同的算法控制参数下运行,星号点表示改进后,菱形点表示改进前,输出结果如图10所示。 图10 引进邻域搜索前后非支配解集的分布Fig. 10 Distribution of non-dominated solution set before and after introducing neighborhood search 令引进近邻搜索后的非支配解集为X2,引进之前为X1,计算结果如表5所示。 表5 引入邻域搜索后两组非支配解集性能对比 两组非支配解集性能计算可以得知,引进邻域搜索以后,得到的非支配解集在收敛性测度优于之前的非支配解集。但近邻搜索并不能够使非支配解集的丰富度和均匀度增加,即近邻搜索并不能够消除种群中个体大量重复的现象。 由2.3和2.4两小节得到的结果可知,单独引进种群均匀度和近邻搜索在提高算法某一方面性能的同时,另一方面算法的性能却并没有得到提高。因此,同时引入近邻搜索和种群均匀度,对算法进行综合优化,仍然采用程序并行的方式,星号点表示改进后得到的非支配解集,菱形点表示标准NSGA2算法得到的非支配解集,两个相同的初始种群在相同的算法控制参数下运行,改进前后的非支配解集如图11所示。 图11 综合改进前后非支配解集的分布Fig. 11 Distribution of non-dominated solution set before and after comprehensive improvement 令改进之后的非支配解集为X2,改进之前为X1,计算结果如表6所示。 表6 综合改进后两组非支配解集性能对比 因此,2个方面同时可进行改进后,非支配解集的收敛性和丰富度测度均得到了提高,算法的综合性能得到改进。将改进前后2组解在同一合格数下的平均质量损失进行对比,如表7所示。 表7 综合改进前后两组解同一合格数下的平均质量损失对比 由表7可知,算法经过综合改进之后,同一合格数的选择装配方案,改进后评价质量损失降低了10.9%到22.2%之间,这表明改进后的选择装配方案装配精度更高,装配质量更好。 1)当种群存在重复个体时,种群的均匀度和丰富度是正相关关系,均匀度越大,种群中相异个体数量也随之越大。以种群均匀度和拥挤度相结合的子代精英保留策略会抑制个体大量重复,提高非支配解集的丰富度,从而扩大解的分布范围,但会降低解集的收敛性。 2)采用近邻搜索以后,会得到许多优于原来的非支配解,提高解集收敛性,但并不能提高大种群的丰富度和均匀度。 3)当同时引进种群丰富度和邻域搜索后,非支配解集的综合性能得到改进,算法的进化速度和收敛速度得到提高。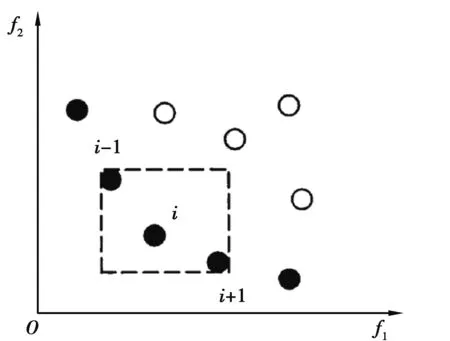
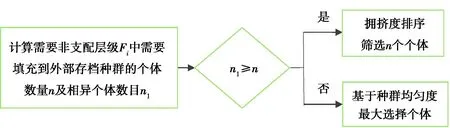
2.3 基于种群均匀度与拥挤度相结合的子代精英保留策略的应用
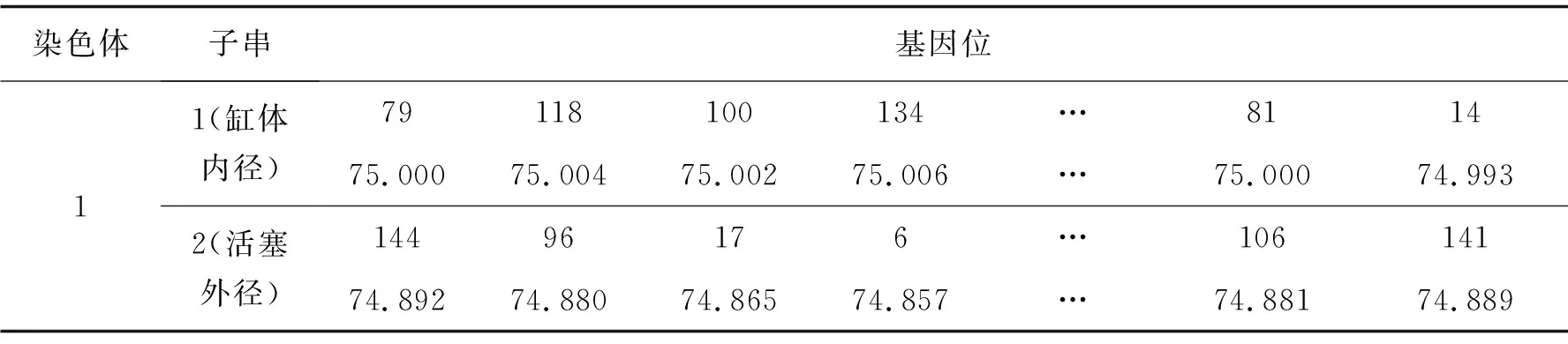


2.4 近邻搜索

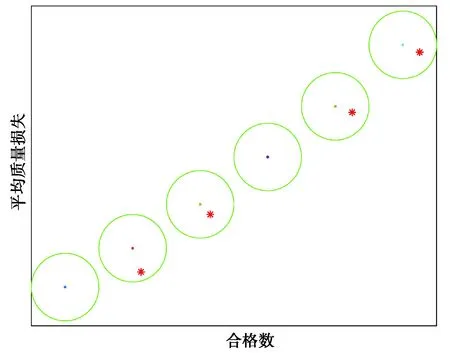

2.5 NSGA2算法的综合改进


3 结 论

