齿轮副非线性接触特性与动力学耦合分析方法

常乐浩,袁冰,宋文,贺朝霞

(1.长安大学道路施工技术与装备教育部重点实验室,710064,西安;2.西安工业大学机电工程学院,710021,西安; 3.中船重工第七○五研究所,710075,西安)

由于时变啮合刚度、制造/安装误差和齿轮侧隙等因素的影响,齿轮系统表现出典型的非线性振动特征。齿轮系统非线性动力学长期以来都是国内外学者研究的热点问题。以往关于齿轮系统非线性动力学的研究多为齿侧间隙因素引起的。Blankenship和Kahraman[1]较早地建立了含齿侧间隙的齿轮副单自由度动力学模型,搭建了振动测试系统[2-3],验证了仿真计算中出现的响应幅值跳跃、分叉和混沌运动等非线性现象。随后的国内外关于齿侧间隙动力学的研究多基于此理论模型,进一步改进了建模方法或者增加了激励因素。例如:Byrtus等[4]利用模态综合法建立了两级齿轮系统动力学模型;文献[5-9]分别增加了齿面摩擦、齿根裂纹、偏心率波动和非线性轴承力等对系统非线性动力学行为的影响。这些模型中,普遍将齿侧间隙作为导致齿轮脱啮、产生非线性现象的主要因素。

然而,齿轮啮合过程本质上是一个复杂的三维动态接触问题。一方面,齿轮接触特性相关的啮合刚度和综合啮合误差为系统振动提供激励;另一方面,动态位移反作用会改变动态接触状态,进一步改变振动激励,所以齿轮接触与系统振动之间存在显著的耦合作用。除了齿侧间隙因素之外,理想齿轮以及含误差或修形的齿轮在振动位移的反作用下,也会使系统产生非线性响应。动态接触有限元法可以有效地预测上述齿轮副瞬态振动特性的变化,但存在预处理复杂、计算工作量大和收敛性差等问题[10-11]。早在1978年,Kubo[12]就提出计入齿面误差和动态位移影响的动态啮合刚度、齿面动态接触应力的计算模型,并发现了共振区的轮齿脱啮现象。随后,王涛等[13]和Cai等[14]等建立了类似的模型,预测到了含误差齿轮的非线性响应。Matsumura等[15]和Andersson等[16]也仿真发现了齿轮动态接触状态与静载时的显著不同。Cao和Chen等[17]建立了考虑载荷相关的直齿轮副动态啮合刚度,分析了载荷和偏心误差对系统非线性振动的影响。Velex等[18]和Ajmi等[19]利用简单的离散刚度模型来代替复杂的接触分析模型,建立了考虑齿面误差分布的动态啮合刚度和动力学模型。Parker等[20]、Eritenel等[21-22]和Dai等[23]分别采用有限元方法、集中质量法和混合解析模型模拟了齿轮副动态接触过程。他们的研究发现,由于振动位移过大,无侧隙的理想或修形齿轮在共振时均可能出现轮齿完全脱啮等非线性现象。Liu等[24]建立了考虑三维接触的齿轮-轴系统多体动力学模型,并与接触有限元结果进行了对比。

总体而言,国内现有文献中对齿侧间隙非线性动力学的研究已较为透彻,但对文献[12-24]所涉及的非齿侧间隙因素引起的非线性动力学现象的规律还研究较少。本文考虑齿轮在动态啮合过程中啮合激励与响应间的相互作用关系,提出了基于切片法的齿轮副动态承载接触分析(dynamic loaded tooth contact analysis,DLTCA)模型,将齿轮副瞬时接触分析与系统动力学求解相结合,建立了齿轮系统“激励-响应-反馈”相闭环的动力学耦合分析方法,以更深层次地研究系统非线性响应的规律。

1 齿轮副弯-扭-轴动力学模型

由于接触问题和动力学求解均涉及非线性方程,所以为了减小计算规模,本文采用集中质量法建立齿轮副的动力学模型。当不考虑两齿轮间的滑动摩擦力时,计入弯曲-扭转-轴向自由度耦合的单对斜齿轮副动力学模型如图1所示。图中,下标p表示主动轮,下标g表示从动轮。

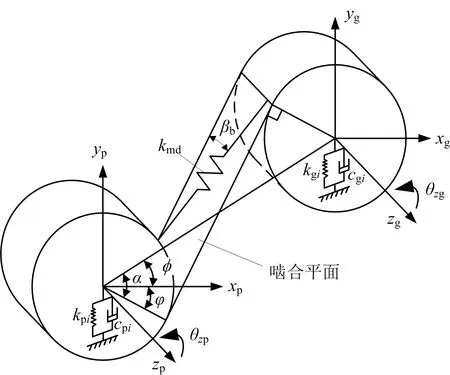
图1 斜齿轮副集中质量动力学模型Fig.1 Lumped parameter dynamic model of a helical gear pair

将图1中两齿轮在各方向的振动位移均向啮合线方向投影,可得齿轮副动态传递误差qd为

qd=VX

(1)

式中:X={xp,yp,zp,θzp,xg,yg,zg,θzg}T为两齿轮位移列向量;V为投影向量,表达式为

(2)

其中,rp、rg为两齿轮基圆半径,βb为基圆螺旋角,φ=α-φ,α为啮合角,φ为安装相位角。

齿轮沿法向的动态啮合总变形为

δ=qd-emd

(3)

式中emd为动态综合啮合误差,将在第2节动态承载接触分析中得到。

由牛顿第二定律可得系统运动微分方程组为

(4)

式中:mi(i=p,g)分别为两齿轮质量;Izi(i=p,g)分别为两齿轮绕z轴的转动惯量;kmd为齿轮副动态啮合刚度;cm为齿轮副啮合阻尼;kij、cij(i=p,g;j=x,y,z)分别为齿轮i沿j向的支承刚度和阻尼;T1和T2分别为两齿轮的扭矩。

啮合阻尼cm为

(5)

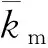
将式(3)代入式(4)中,并整理成矩阵形式

(6)

式中:M、C和K分别为系统质量矩阵、阻尼矩阵和刚度矩阵;e为综合误差向量,e=emdVT;P为外载荷向量。

2 动态承载接触分析

2.1 动态接触方程的建立与求解

以往学者在建立齿轮副的承载接触模型时,多是在静态情况下完成的，即假定齿轮副在已知外载荷P的作用下,两齿轮缓慢靠近并逐渐进入接触状态,求解未知的齿面载荷分布和静态传递误差。本小节将在静态承载接触模型的基础上加以改进,建立齿轮副的动态承载接触模型。

在不考虑摩擦的情况下,当已知齿轮副的动态传递误差时,各接触点变形协调条件可写为

[Cbf]{F}+{uc}-{Y}=qd-{ε}

(7)

式中:[Cbf]为齿面各接触点的线性宏观变形所形成的柔度系数矩阵,主要由轮齿弯曲-剪切变形和轮体变形组成;{F}为载荷列向量;{uc}为接触变形列向量;{Y}为接触后的剩余间隙列向量;{ε}为初始间隙列向量,可以包含齿轮制造误差、修形、齿侧间隙及啮合错位等;qd为按式(1)所定义的动态传递误差。为了避免有限元方法求解时间长的缺点,[Cbf]和{uc}采用切片法理论进行计算,计算公式参考文献[25]。

在接触时,需要满足载荷判别条件

(8)

式(7)、(8)组成了齿轮副在啮合过程中的动态承载接触方程组。在求解时,由于qd可由系统动力学求解得到,可将其视为已知量。判断qd与各点初始间隙εi的关系:若qd≤εi,则将该点方程从总体方程组去除;若qd>εi,则将Yi赋为0。这样非线性接触方程组(7)就只包含未知量{F},可通过常规迭代法求解。

2.2 动态啮合刚度和动态综合啮合误差

齿轮动态啮合刚度是指齿轮副在正常的工作状态下,同时啮合的轮齿所表现出的等效啮合刚度[13]。当求解接触方程得到{F}后,齿轮副动态啮合刚度可由各接触点的动态刚度ki求和得到

(9)

在某一啮合位置的弹性啮合力平衡方程为

(10)

定义动态综合啮合误差为

(11)

齿轮副的总啮合力为

(12)

接触点i的接触应力σci为

(13)

式中:Li为该点分段接触线长度;ρi为综合曲率半径;E1、E2为两齿轮弹性模量;υ1、υ2为泊松比。

从式(9)可以看出:齿轮在动态接触过程中的动态啮合刚度kmd不仅是时变的,同时受齿轮误差和修形等因素的影响;当考虑振动位移的反作用后,其大小还与振动位移相关。同理,动态综合啮合误差emd也与这几个因素相关。反映到系统动力学方程中,即刚度矩阵K和综合误差向量e同时是时间t和位移响应X的函数,导致在求解时必须建立瞬时接触与动力学的耦合分析方法。

3 齿轮接触与动力学耦合分析方法

齿轮的动态啮合过程是包含瞬时接触与系统振动相互作用的“激励-响应-反馈”的闭环耦合过程。从方程上看:当求解瞬时的接触方程(7)后,根据式(9)、(11)可得到系统振动的“激励”——瞬时kmd和emd;将二者代入动力学方程(6)并求解得到系统“响应”——动态位移X;再通过式(1)得到接触方程(7)的“反馈”——qd。以往多数学者在分析系统振动时,只考虑“激励-响应”的单向关系,而未计入系统振动对接触特性的反馈。若要考虑这种反馈关系,必须建立二者之间的闭环耦合分析方法。

本文结合齿轮动态接触问题的特征,提出了基于Newmark-β法的齿面瞬时接触与系统振动耦合求解方法,具体流程如图2所示。

图2 齿轮副瞬时接触与系统振动耦合求解流程Fig.2 Flow chart of solving the coupling model of transient contact and system vibration of the gear pair

4 模型验证

以文献[2]中的齿轮系统动态响应试验为依据,验证本文提出的齿轮接触与动力学耦合模型的正确性。该试验台为美国the Ohio State University齿轮实验室搭建的一套用于圆柱齿轮副振动测试的装置,已被用来开展齿廓修形和重合度对直齿轮非线性振动的影响研究、齿侧间隙引起的幅值跳跃等现象研究。由于测量仅得到扭转方向的位移,所以在计算时也只取传递误差在扭转方向的位移分量。

试验齿轮的基本参数如下:主动轮和从动轮齿数均为50,分度圆压力角为20°,齿宽为20 mm,齿顶圆直径分别为154.41 mm和154.71 mm。根据文献[2]的描述,系统在各转速和扭矩时的阻尼比都在0.02左右,所以本文在计算时选取齿轮副的啮合阻尼比为0.02。同时,取轴承的径向刚度均为5×108N/m,轴承的阻尼为1×104N·s/m。在输入扭矩为170 N·m时,采用本文方法计算的qd波动部分均方根qdr与试验的对比如图3所示。qdr的计算式为

(14)

图3 本文计算的动态传递误差和试验结果对比Fig.3 Comparison of qd by simulation and experiment

试验结果表明,在共振转速附近,系统表现出强烈的非线性响应,并出现了典型的响应幅值跳跃现象。同时,升速过程中的幅值上跳频率要大于降速过程中的幅值下跳频率,形成了跳跃滞后环。在二次谐波共振区,升速和转速时所对应的响应幅值也略有差异,但滞后环宽度和跳跃幅值相比主共振区要小许多。与试验结果相比,本文的计算结果能够准确地捕捉到由于轮齿分离引起的非线性响应,各频率下的响应幅值和跳变频率也与试验数据基本吻合,体现出很高的准确性。因此,本文所提出的齿轮接触动力学耦合分析方法在预测系统非线性动力学行为时是有效的。

5 计算结果与分析

以一对新的直齿轮副为例,分析系统非线性响应的特征。主、从动轮齿数分别为31和104,模数为4 mm,分度圆压力角为20°,齿宽为60 mm,轴承刚度为5×108N/mm。动态传递误差qd按照式(1)进行计算。

5.1 啮合阻尼对响应的影响

取输出扭矩为500 N·m,分别计算阻尼比为0.03、0.06、0.09时无误差齿轮副在0～5 000 r/min时的系统响应,结果如图4所示。可以看出,当啮合阻尼比为0.03和0.06时,传递误差均方根qdr在主共振转速处存在幅值跳跃现象,且升速和降速过程所对应的跳跃速度有所差异,形成跳跃滞后环。当阻尼比为0.06时,相比阻尼比为0.03时的情况,主共振的滞后环有所减小,二次谐波处的滞后环消失。当阻尼比为0.09时,升速和降速过程中的跳跃现象消失。在主共振和高次谐波共振区外,不同阻尼比的响应幅值差异不大。这是由于对于阻尼振动系统,当激励频率接近系统共振频率时,系统进入阻尼控制区,响应幅值主要受阻尼影响。当激励频率远离共振频率时,阻尼的影响作用将显著减小。

图4 不同啮合阻尼比对动态响应的影响Fig.4 Effects of mesh damp on the dynamic responses

5.2 不同转速下的激励与响应对比

取阻尼比为0.03,分析动态激励在不同转速下的变化规律。以升速过程为例,系统转速为2 950 r/min时，开始出现脱啮现象,导致振动响应值相比2 900 r/min时有了大幅提高,即出现了幅值上跳现象。分别选取转速为100、2 900、2 950、5 000 r/min,提取各转速下的动态啮合刚度、动态传递误差和动态啮合力,结果如图5～7所示。可以看出,当转速为100 r/min和5 000 r/min时,系统振动位移较小,齿面并未出现完全脱啮现象,动态啮合刚度与静态时基本相同,即呈现矩形波形式。100 r/min时的动态啮合力与静态啮合力基本相等,5 000 r/min时的动态啮合力稍有增大。在2 900 r/min时,一个啮合周期内的动态传递误差有接近于0的部分,相应的动态啮合力也接近于0,动态啮合刚度有所减小。转速变为2 950 r/min时,齿轮副出现脱啮区域,在该区域内传递误差小于0,啮合刚度和啮合力均为0。此时,动态传递误差和啮合力波动显著增加,系统呈现共振状态。由于分析对象为理想齿轮,所以所有转速下的动态综合啮合误差始终为0。

图5 不同转速下的动态啮合刚度对比Fig.5 Dynamic mesh stiffness at different rotational speeds

图6 不同转速下的动态传递误差对比 Fig.6 Dynamic transmission error at different rotational speeds

图7 不同转速下动态啮合力对比Fig.7 Dynamic mesh force at different rotational speeds

分别观察4种转速下齿面的动态接触应力,如图8所示。可以看出,不同转速下的齿面动态接触应力有显著的区别。当转速为100 r/min时,齿面的接触应力与静态时基本相同,即单齿区的接触应力要明显大于双齿区的,单双齿交界处的接触应力出现突变。当转速为2 900 r/min时,最小接触应力接近于0。当转速为2 950 r/min时,出现了接触应力为0的区域,即完全脱啮区,最大接触应力在几个所选取的转速中最大。当转速为5 000 r/min时,虽然动态啮合刚度与100 r/min时基本相等,但齿面接触应力分布与100 r/min时有着明显的差距,说明动态位移对接触状态有着较大影响。

(a)100 r·min-1

取转速为2 500 r/min,分别对比升速和降速时齿面的动态接触状态、动态啮合刚度和动态啮合力,结果如图9和图10所示。从图9可以发现,升速经过2 500 r/min时,齿面最小接触应力不为0,即齿面处于完全接触状态,而降速经过2 500 r/min时,最大接触应力比升速时明显提高,部分齿面的接触应力为0,即出现完全脱啮状态。这说明当计入齿轮接触与振动耦合作用后,系统表现出明显的非线性特性,特别是在共振转速附近的响应对初始条件非常敏感,初始条件不同会导致系统响应出现显著差异。从图10可以看出,升速时齿轮副动态啮合刚度始终大于0,且动态啮合力波动量较小,而降速时齿轮副动态啮合刚度和动态啮合力均出现部分为0的区域,动态啮合力幅值比升速时显著增大。

(a)升速

(a)动态啮合刚度

5.3 修形和齿侧间隙的影响

选取修形方式为直线型齿廓修形,啮合平面上对应的修形量为5 μm,修形长度为0.3pbt,pbt为端面基节。保持载荷不变,计算得到不同转速下的响应,结果如图11所示。可以看出,对于给定的修形参数,系统仍然出现了响应幅值跳跃的现象。但是,在多数转速下,动态传递误差相比无修形时都有所降低,且共振区的最大幅值以及升降速响应幅值跳跃形成的滞后环都显著减小。这说明合适的修形参数可以降低系统非线性响应的程度。

图11 修形对动态响应的影响Fig.11 Effects of tooth modification on the dynamic responses

取单侧齿侧间隙为5 μm,且不考虑齿背接触状态,计算动态传递误差均方根和均值随转速的变化过程,结果如图12和图13所示。可以看出,计入侧隙后,qd均方根在不同转速下与不计入时几乎完全相等,而qd均值的曲线形状也基本一致,区别在于考虑侧隙后的qd均值比不考虑时正好大了原始侧隙尺寸5 μm。此结果可以反映出,使齿轮产生非线性响应的真正原因在于动态啮合刚度随振动位移的变化,齿侧间隙只是影响了振动均值。

图12 计入齿侧间隙后qdr的变化Fig.12 Root mean square of qdr with tooth clearance

图13 计入齿侧间隙后qd均值的变化Fig.13 Mean value of qd with tooth clearance

5.4 静态与动态接触激励模型的对比

通过前述分析可知,考虑瞬时接触与系统振动耦合的动力学模型能够很好地获取系统非线性响应。然而,由于求解规模大,对于复杂传动轮系或者分布质量法建立的多自由度模型,计算效率将显著下降。传统的采用静态接触激励的动力学模型不需要进行瞬时接触分析,所以计算时间大幅减小。本小节着重对比这两种激励模型的差异。

分别计算无误差齿轮副在螺旋角为0°和10°时,采用两种激励模型的动态响应，结果如图14和图15所示。从图14可以看出,静态激励动力学模型无法捕捉到齿轮副在共振转速响应幅值跳跃的强非线性动力学行为。但是,当输入转速远离系统共振转速时,两种激励的计算结果具有高度一致性。当螺旋角增加到10°后,系统的非线性响应消失,各转速下动态响应差异非常小。在计算时间方面,静态激励动力学模型省去了每个积分时刻的DLTCA过程,所以计算时间显著缩短。在CPU为Core i7 10代的微型计算机上运行,采用动态激励和静态激励的计算时间分别为20 min和10 s左右。因此,可在初始设计阶段,利用静态接触激励动力学模型预测共振转速区间,指导齿轮宏观参数设计。

图14 直齿轮不同类型激励的响应对比Fig.14 Dynamic responses of a spur gear pair with dynamic excitation and static excitation

图15 斜齿轮不同类型激励的响应对比Fig.15 Dynamic responses of a helical gear pair with dynamic excitation and static excitation

6 结 论

本文提出了齿轮动态承载接触分析模型,结合集中质量法,建立了齿轮瞬时接触分析与系统振动联合求解方法,形成系统“激励-响应-反馈”闭环动力学分析流程,并分析了啮合激励与动力学响应间的相互作用关系。研究发现:

(1)由于齿面瞬时接触特性与系统振动之间的相互影响,齿轮的动态啮合刚度和动态综合啮合误差与静态接触时差别较大,使齿轮系统表现出强烈的非线性特性。在升速和降速过程的共振区附近,系统振动幅值较大,齿面可能出现完全脱啮现象,从而产生响应幅值跳跃。同时,由于升降速跳跃转速的不同,使系统响应形成典型的滞后环。

(2)啮合阻尼主要影响共振区附近的动态响应,对非共振区的响应影响不大。增加啮合阻尼和螺旋角后均会使系统非线性特性减弱,直至消失。

(3)合理的修形参数能够降低系统非线性响应的程度。齿侧间隙主要影响非线性响应的均值,但对响应幅值的影响并不明显。

(4)齿轮的非线性响应主要表现在共振区附近,在非共振区采用静态激励和动态激励所计算的响应结果差异并不大。

与常规齿侧间隙动力学相比，本文方法的优点在于在动力学求解时增加了齿轮副动态接触分析,不仅能计入齿侧间隙的影响,还可以考虑齿轮误差、修形等因素,能够计算齿轮副在振动过程中的动态激励和接触特性,获得更为丰富的动态响应结果,可作为齿侧间隙动力学的有效补充。限于篇幅,本文只针对这些因素进行了初步分析。后续,可深入地对这些参数的影响规律以及系统动力稳定性等方面进行研究,以更深层次地把握齿轮系统非线性动力学特征。