泡沫阻力因子与残余阻力因子预测模型研究

周新宇 黄 佳 韩 璐 刘 章, 蔡红岩 贾宁洪 胡景宏

1. 提高石油采收率国家重点实验室(中国石油勘探开发研究院),北京 100083;2. 中国地质大学(北京)能源学院,北京 100083

0 前言

泡沫驱凭借其良好的调剖封堵效果,被广泛应用于具有“高含水”“高采出程度”双高特点的老油田,可有效降低含水率,稳定单井产量,提高老油田的采收率,是一项很有发展前途的三次采油技术[1-3]。泡沫阻力因子与残余阻力因子是评价泡沫驱封堵性能的重要参数,可表征泡沫的有效黏度和调剖封堵能力[4-7]。理论研究表明,泡沫阻力因子越高,泡沫驱油体系在油层中的波及体积越大,泡沫驱后提高采收率的潜力越大。国内外学者通过大量研究发现:泡沫流体是一种典型的可压缩非牛顿流体,在多孔介质中的渗流阻力受到气液比、流体注入速度、泡沫注入量、岩心渗透率、含油饱和度等诸多因素的影响[8-10]。这些研究大多需要开展大量室内物模驱替实验,通过实验分析各因素对泡沫封堵能力的影响规律,但实验无法明确泡沫驱封堵能力与各影响因素之间存在的确切关系。泡沫注入量决定着实际生产中起泡剂的使用量,关系着油田的生产成本,决定了油田开发经济效益的高低。从众多研究及矿场实验来看,生产过程中泡沫注入量与油藏的孔隙体积有关,常利用孔隙体积倍数(Pore Volume,PV数)来表示泡沫注入量[11-14]。本文研究了岩心渗透率、孔隙度以及泡沫注入量三个主要因素对泡沫在多孔介质中渗流的泡沫阻力因子与残余阻力因子的影响规律,再利用SPSS分析软件,引入逐步回归分析方法[15-20],建立各因素与两种阻力因子的数学模型,并通过室内物模驱替实验对模型进行验证,评估实验模型的精度,结果表明:在确定注入速度、气液比的前提下,利用岩心渗透率、泡沫注入量预测泡沫阻力因子的模型基本满足实际需求,而泡沫阻力因子及残余阻力因子与孔隙度均表现出不相关[21]。通过建立相关预测模型,可以有效减少室内泡沫驱替实验的开展,节省人力物力,提高经济效益[22]。

1 实验部分

1.1 实验设备

实验设备主要包括:恒温箱、驱替泵、中间容器、泡沫发生器(死体积2 mL),岩心夹持器、高精度压力表、回压阀、液体计量管、气体流量计以及阀门等。

1.2 实验流程

实验流程见图1。

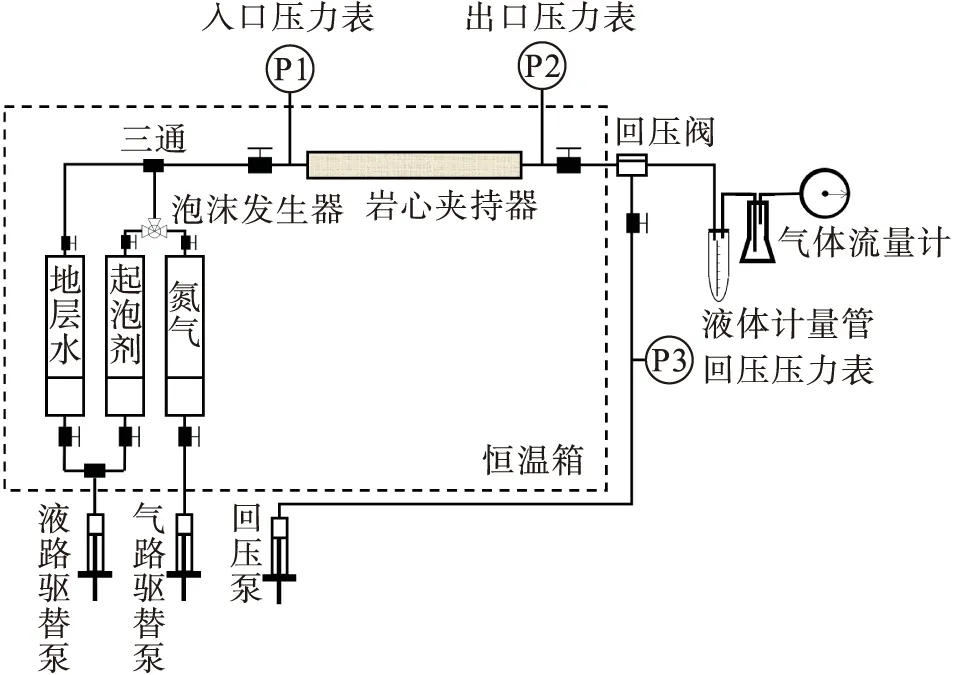
图1 泡沫驱实验流程图Fig.1 Flow chart of foam flooding experiment

1.3 实验条件及方案设计

本文主要通过在室内开展泡沫封堵性评价实验,拟定研究的影响因素包括:岩心渗透率、孔隙度以及泡沫注入量3个因变量,然后将这3个因变量选定8个大小不同等级。实验材料方面:起泡剂质量浓度为0.4%,选用惰性气体氮气作为起泡的气体,选用气液比为2∶1,利用模拟地层水测试岩心渗透率,前置水驱,泡沫段塞过程中各阶段流体注入总速度为0.5 mL/min,各模拟实验具体方案及岩心参数见表1。

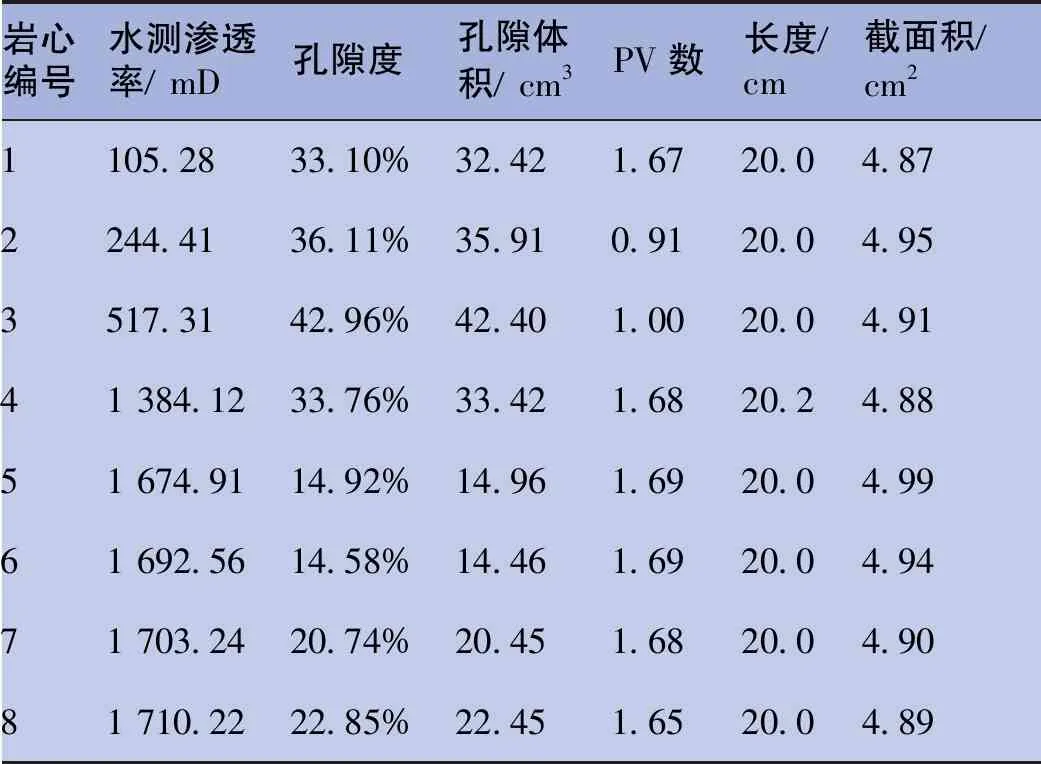
表1 多因素分析模拟实验方案及岩心参数表Tab.1 Multi-factor analysis simulated test plan and core parameters

1.4 实验步骤

1)测量岩心的长度L,直径d,并由此得出岩心的体积V1。

2)将岩心置于恒温箱中烘干8 h,称取干重m1。

3)将岩心抽真空6 h后,饱和模拟地层水,称取湿重m2,通过式(1)计算填砂模型孔隙度φ:

φ=(m2-m1)/ρV1

(1)

4)将经过充分饱和的岩心放置到岩心夹持器内,按照实验流程连接,设定回压10 MPa,环压14.6 MPa,在49 ℃的条件下恒温12 h。

5)以0.5 mL/min的流速水驱,测量岩心渗透率,并记录压差p1。

6)以0.5 mL/min的总流速注入气液比为2∶1的泡沫,并记录压差p2,通过公式(2)计算泡沫阻力因子RF:

(2)

7)以0.5 mL/min的流速进行后续水驱,记录岩心管两端压差p3,通过公式(3)计算残余阻力因子RFr:

(3)

式中: φ为填砂模型孔隙度,无量纲;m1为干重,g;m2为湿重,g;ρ为地层水密度,g/cm3;V1为填砂模型体积, cm3;p1为水驱平衡时压差,MPa;p2为泡沫段塞平衡时压差, MPa;p3为后置水驱平衡时压差, MPa;RF为泡沫阻力因子;RFr为残余阻力因子。

1.5 实验结果

以1号岩心为例开展室内泡沫封堵性评价单组实验,实验过程中泡沫阻力因子、残余阻力因子随注入流体PV数变化曲线见图2。受段塞注入量的影响,泡沫阻力因子取泡沫驱阶段结束前一段时间内相对稳定值的平均值为该组实验的泡沫阻力因子,残余阻力因子取后续水驱阶段结束前变化幅度不大的一段数据的平均值,以此方法统计所有岩心实验数据，见表2。

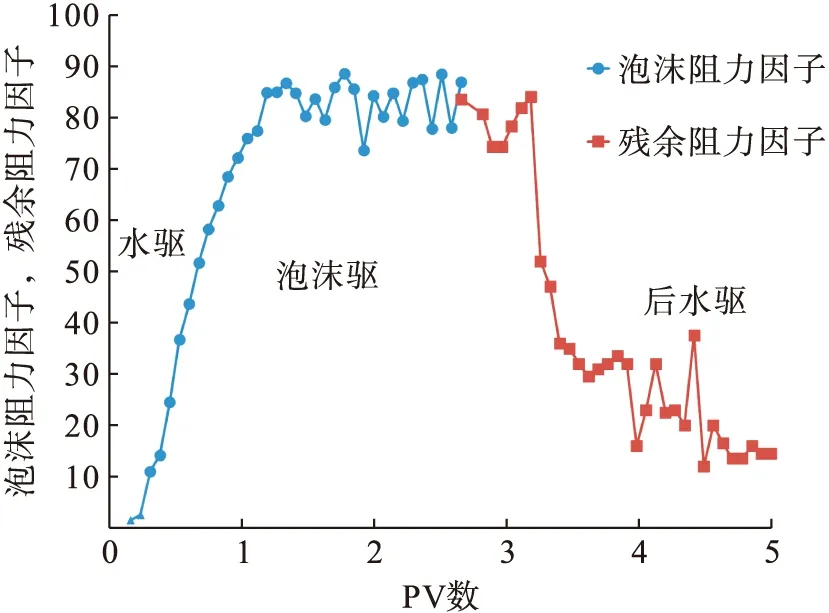
图2 泡沫阻力因子/残余阻力因子随注入流体PV数变化曲线图Fig.2 Foam resistance factor/residual resistance factor curve with injection pore volume

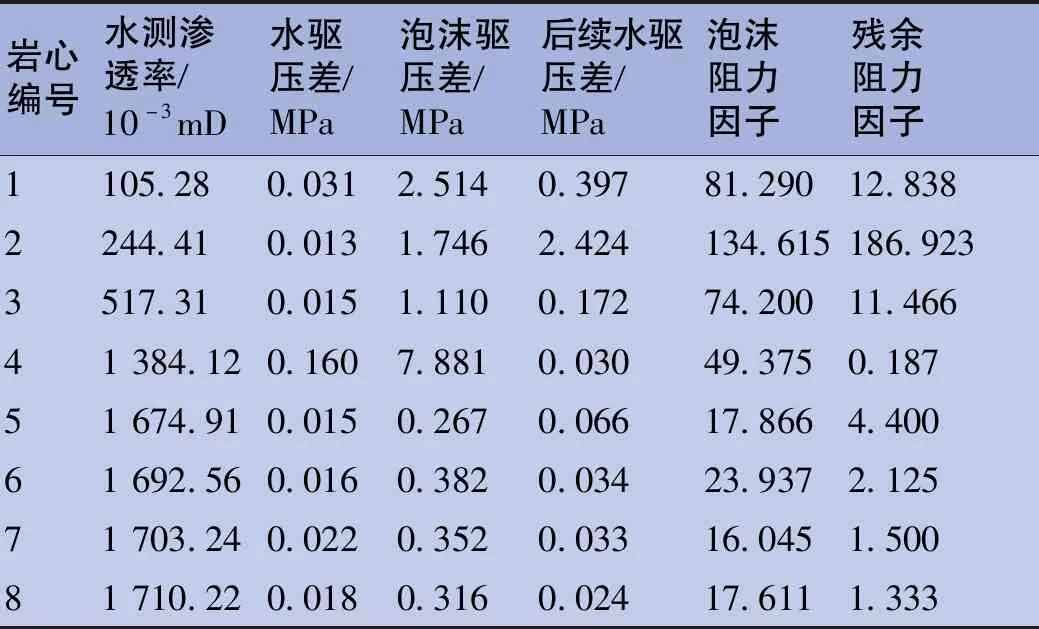
表2 泡沫阻力因子及残余阻力因子影响因素实验结果表Tab.2 Experimental results of the influence factors of foam resistance factor and residual resistance factor

2 预测模型的建立与检验

2.1 预测模型的建立

预测模型的建立运用到了逐步回归分析法,该方法的基本思想是通过剔除变量中不太重要但又和其他变量高度相关的变量,以此来降低多重共线性程度。从自变量X1开始,检验自变量X1对因变量Y作用的显著程度,将X1至Xn从大到小地依次逐个引入模型。当自变量Xn-k由于后面k个变量的引入而变得不显著时,要将其删除[23]。引入自变量或者从模型中剔除一个自变量,则为逐步回归分析的一步。整个分析过程中对每一步都要进行F值检验,以确保每次引入新的显著性变量前回归方程中都只包含对因变量Y作用显著的变量。这是一个反复迭代的过程,直到既没有显著的解释变量引入模型,也没有不显著的解释变量从模型中被删除为止,以保证最后所得到的解释变量集是最优的[24]。

2.1.1 各因素对泡沫阻力因子的影响

利用SPSS分析软件对泡沫阻力因子进行逐步回归分析,得到结果见表3。

表3 泡沫阻力因子逐步回归分析结果表Tab.3 Stepwise regression analysis results of foam resistance factors

将岩心渗透率、孔隙度、泡沫注入量作为自变量,而将泡沫阻力因子作为因变量进行逐步回归分析,经过模型自动识别,最终余下岩心渗透率、泡沫注入量2项变量在模型中,模型公式为:

RF=163.856-0.038K-52.099q

(4)

式中:K为渗透率,mD;q为泡沫注入量,用PV数表示。

从表3可知，R2数值为0.907,这意味着岩心渗透率、泡沫注入量可以解释泡沫阻力因子90.7%的变化原因,而且模型通过F值检验(F=24.263,p=0.003<0.05),该结果说明模型有效。其中,渗透率的回归系数值为-0.038(t=-3.258,p=0.022<0.5),这意味着渗透率会对泡沫阻力因子产生显著的负向影响,再结合泡沫阻力因子的定义式,通过将泡沫驱与水驱压差求比值消除了渗透率对压差的影响,再结合模型,可以确定随着渗透率升高,泡沫阻力因子会随之降低,如果要确保泡沫阻力因子保持在一定的水平,需要考虑从其他因素着手;而注入量的回归系数值为-52.099(t=-2.494,p=0.055>0.05),这意味着注入量并不会对阻力因子产生显著影响。

2.1.2 各因素对残余阻力因子的影响

利用 SPSS 分析软件对残余阻力因子进行逐步回归分析,得到结果见表4。

表4 残余阻力因子逐步回归分析结果表Tab.4 Stepwise regression analysis results of residual resistance factor

将岩心渗透率、孔隙度、泡沫注入量作为自变量,而残余阻力因子作为因变量进行逐步回归分析,经过模型自动识别,最终余下泡沫注入量在模型中,模型公式为:

RFr=231.009-145.579q

(5)

式中:RFr为残余阻力因子。

R2值为0.679,这意味着泡沫注入量仅可以解释残余阻力因子67.9%变化原因,考虑到相关性不高,说明用逐步回归的方法无法获得残余阻力因子关于岩心渗透率、孔隙度、泡沫注入量相关性较高的预测模型。针对此情况,考虑将残余阻力因子与泡沫注入量进一步利用SPSS分析软件做非线性回归分析,得到结果见表5。

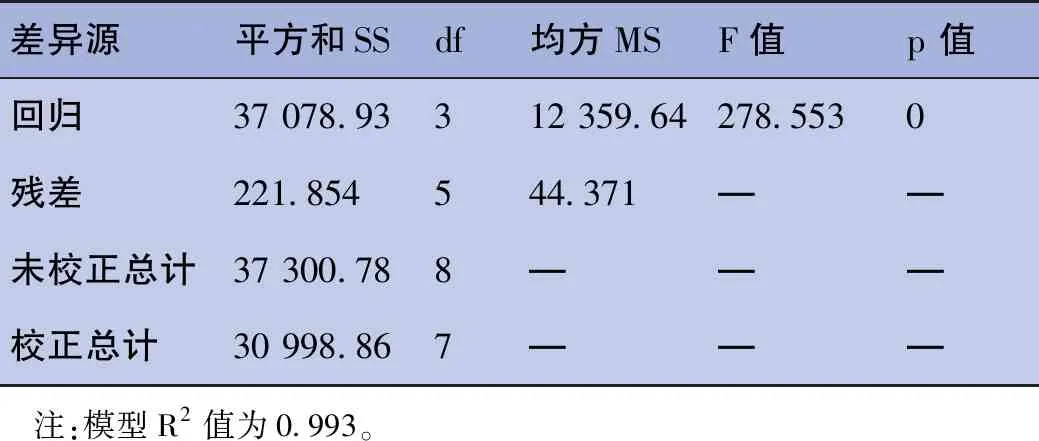
表5 残余阻力因子非线性回归分析结果表Tab.5 Non-recurrence regression analysis results of residual resistance factor

从表5可知,模型公式为:

RFr=940.470-1 549.38q+603.388q2

(6)

其中模型R2值高达0.993,具有高度相关性参数b1为940.470,95%CI为814.866～1 066.075,这其中不包括数字0,意味着其呈现出统计学意义;参数b2为-1 549.380,95%CI为-1 793.662～-1 305.097,这其中不包括数字0,意味着其呈现出统计学意义;参数b3为603.388,95%CI为498.650～708.127,这其中不包括数字0,意味着其呈现出统计学意义。

2.2 预测模型的检验

为了验证预测模型利用岩心渗透率、孔隙度、泡沫注入量这3个因素预测泡沫阻力因子和残余阻力因子的准确性,选取2根具有不同渗透率的岩心在室内展开物模驱替实验,采取不同的泡沫注入量,各段塞流体注入速度仍选用0.5 mL/min,氮气与起泡剂的气液比为2∶1,实验结果见表6。

表6 预测模型的实验结果表Tab.6 Test results of the prediction model

通过实验对比发现,模型针对泡沫阻力因子RF的预测具有较高的预测精度,3组实验的数据预测精度在80%左右,模型主要是受岩心渗透率与泡沫注入量的影响,与孔隙度无关。这是因为泡沫段塞是一个动态运移过程,岩心渗透率是反映流体在多孔介质中运移的宏观流动状态,岩心渗透率大小可间接反映多孔介质中孔隙联通的有效性,岩心渗透率对模型影响显著,预测精度说明基本上可以借助模型预测出泡沫阻力因子。而模型针对残余阻力因子预测精度则相对较差,这是因为泡沫阻力因子与残余阻力因子的确定都是一个动态过程,二者的取值均是取统计学意义上的平均值,因此误差相对较大,但通过多组实验验证发现:随着岩心渗透率的上升,残余阻力因子预测模型的精度逐渐上升,当岩心渗透率处于高渗—特高渗范围时,预测精度相对较高,达到55%左右。这是因为实验过程中使用的泡沫段塞配方属于多元复合体系,成分组成相对复杂,为增加泡沫的稳定性,配方中还混有一定量的聚合物。泡沫体系被注入到地层中时,当地层渗透率越高,这些颗粒越容易进入孔渗透条件较好的其他区域,在地层中发挥调剖效果,相比中低渗地层,其波及范围更高,使用泡沫段塞前后形成的泡沫以及聚合物对孔渗条件更好的地层影响更大,改善更充分。因此,残余阻力因子预测模型的精度随着岩心渗透率的增大而相应提高。

3 结论

1)通过室内物模驱替实验,在控制气液比、注入速度不变的情况下,通过分析多孔介质的岩心渗透率、孔隙度、泡沫注入量对驱替过程中泡沫阻力因子、残余阻力因子的影响,发现泡沫阻力因子与岩心渗透率、泡沫注入量有关,与孔隙度无关,而残余阻力因子仅与泡沫注入量有关。

2)岩心渗透率会对泡沫阻力因子产生显著的负向影响,岩心渗透率越高,泡沫阻力因子越小,但注入量并不会对泡沫阻力因子产生显著影响,因此当岩心渗透率较高时,为保证在泡沫驱阶段具有较高的泡沫阻力因子,应当从其他因素着手,以此来确保泡沫封堵性满足实际生产需要。

3)通过逐步回归分析,得出泡沫阻力因子关于岩心渗透率与泡沫注入量的预测模型,经过3组检验实验验证,模型预测精度达80%,对实际生产具有一定的指导意义;残余阻力因子预测模型经检验,当渗透率达到高渗—特高渗范围时,模型精度能够达到55%,说明模型存在一定的适用范围。