弱电网环境下基于Super-Tw isting的单相并网逆变器电流控制策略

徐国荣，滕青芳，2

（1.兰州交通大学自动化与电气工程学院，兰州 730070；2.兰州交通大学甘肃省轨道交通电气自动化工程实验室，兰州 730070）

近年来，随着节能、高效、低碳的能源需求，分布式并网发电项目得到了长足的发展.由于并网逆变器是连接分布式电源和大电网的必备接口，因此，对并网逆变器的稳定性及控制方法的研究得到越来越多学者的重视［1］.考虑到常见的分布式电源，比如光伏、风电，其实际地理位置分布往往偏离负荷中心，在这种情况下长距离的输电线路及变压器的漏抗会使得大电网呈现为弱电网的特性［2-4］.在弱电网环境下，由于电网阻抗的时变特性［5］会影响并网逆变器注入电网的并网电流质量，使得对并网逆变器在弱电网环境下的控制方法提出了更高的要求.

为了消除电力电子器件产生的开关次谐波对并网电流质量带来的不良影响，各种类型的滤波器被广泛地使用，如L型、LC型和LCL型滤波器.相比于其他两种滤波器而言，LCL型滤波器具有更优越的滤波性能和更小的空间体积，因此得到了更多的关注；然而，LCL型滤波器造成的谐振尖峰问题会影响并网系统的并网电流质量，甚至使得系统不能稳定运行［6-7］，因此，必须对此问题进行抑制.为了抑制LCL型滤波器存在的固有谐振问题，目前采取的方法大体上可以分为有源阻尼方法和无源阻尼方法两大类.文献［8］提出一种基于陷波器的有源阻尼方法，通过利用陷波器产生一个反向的谐振尖峰来抵消滤波器产生的正向尖峰，然而在滤波器参数存在摄动的情况下会限制其使用场合；文献［9］提出了一种将LCL型滤波器的电容分成两部分的分裂电容有源阻尼方法，该方法设计较为简单，然而并没有分析电网阻抗变化时的情况；文献［10］提出了一种改进的电容电流反馈的有源阻尼控制方法，该方法通过添加相位补偿环节，增大了有源阻尼的适用范围，然而并没有考虑滤波参数的摄动；文献［11］提出了一种将电容电流反馈和传统的加权平均电流（weighted average current，WAC）反馈相结合的改进控制方法，该方法优化了并网电流质量，提高了系统的鲁棒性.

此外，由于前级电压源的波动、LCL型滤波器滤波参数的摄动及电网阻抗的变化都会对逆变器最终输出的并网电流质量造成一定程度的不利影响，因此，设计一种使得并网逆变器系统在应对各种扰动时依然保持较好的动、稳态性能并且具有强鲁棒性的控制策略具有重要的工程价值.目前，对于逆变器系统控制策略的研究而言，主要沿着经典线性控制和现代非线性控制两个方向推进.文献［12］为了降低电网阻抗对系统稳定性造成的不良影响，提出了一种输出阻抗矫正的方法，提高了逆变器系统对于电网阻抗变化的适应性；文献［13］设计了一种将谐波补偿装置嵌入到准比例谐振控制器中，提升了并网电流的质量，但是未考虑电网阻抗的影响.近年来，一些先进的非线性控制方法也被广泛应用在电力电子器件中，比如模型预测控制［14］、自抗扰控制［15］、H∞控制［16］、滑模控制（sliding mode control，SMC）等.在这些非线性控制方法中，由于SMC设计简单且对外部扰动和系统参数摄动等不确定性有较强的抑制能力而受到了更多的关注，然而常规SMC由于切换运动的存在使得控制过程存在“抖振现象”.文献［17］通过设计一种使用改进型幂次趋近律的SMC有效降低了抖振，改善了并网性能，但是未考虑滤波参数摄动带来的影响；文献［18］考虑了逆变器系统中的负载变化和参数变化，设计了一种基于超扭曲（super-twisting，ST）算法的鲁棒电压控制方法，加强了系统的抗干扰能力，但是未考虑并网时电网阻抗的影响.

在已有研究成果的基础上，针对LCL型单相并网逆变器系统中传统的控制器对电网阻抗变化的适应性不强和参数摄动的鲁棒性不足的缺点，本文设计了一种混合阻尼方法下基于超扭曲滑模控制器（super-twisting sliding mode controller，STSMC）的单相并网逆变器鲁棒电流控制策略，然后将基于STSMC的单相并网逆变器系统和基于SMC的单相并网逆变器系统在 Matlab／Simulink仿真平台和硬件在环（hardware in the loop，HIL）实验平台上的结果进行对比，从而进一步验证所提控制方法的有效性.

1 弱电网下不同阻尼方法的特点及单相并网逆变器系统的建模

1.1 电网阻抗对于不同阻尼方法的影响

1.1.1 无源阻尼方法

基于无源阻尼控制方法的单相并网逆变器系统框图如图1所示.图1中，Udc为逆变器直流侧母线电压，Ug为电网侧电压，L1，C1，L2分别为逆变器侧电感、滤波器电容和网侧电感，i1为逆变器侧电流，ig为并网电流，Uab为逆变器侧输出电压，UPCC为并网点电压，Rd为阻尼电阻，考虑到对稳定性最恶劣的情况，取电网阻抗为纯感性，即电网阻抗为Lg.

根据图1，无源阻尼控制方法下，并网逆变器输出并网电流ig至逆变器输出侧电压Uab的传递函数为

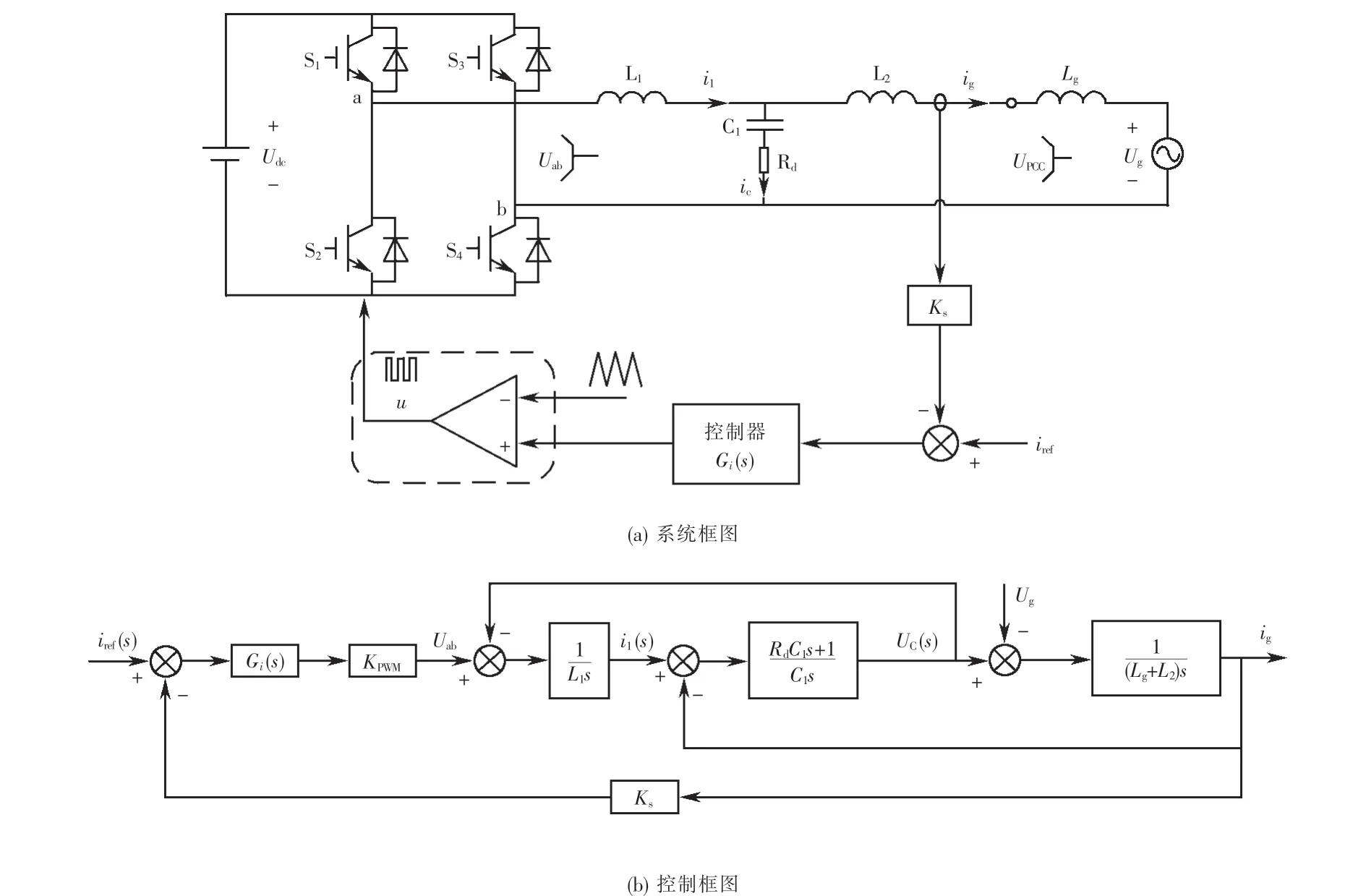
图1 无源阻尼控制方法Fig．1 Passive dam ping control method

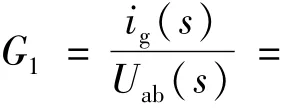
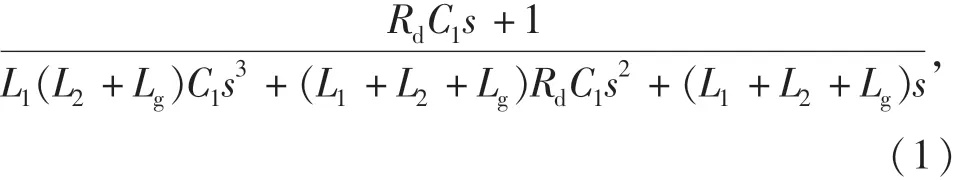
其中：ig（s）为s域中的并网电流；Uab（s）为 s域中逆变器侧输出电压．

图2为单相并网逆变器系统在无源阻尼下G1的Bode图，其中：图2（a）为阻尼电阻取不同值时的Bode图；图2（b）为电网阻抗取不同值时的Bode图.从图2（a）可以看出：随着阻尼电阻的增大，系统对谐振峰的抑制效果越来越明显，但是大的阻尼电阻会带来系统损耗变大的不利后果.从图2（b）可以看出：电网阻抗的变化会导致谐振峰的频率发生移动.

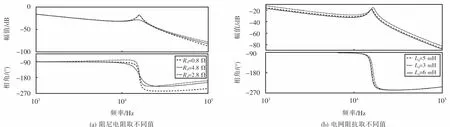
图2 无源阻尼控制方法下系统Bode图Fig．2 Bode diagram of system under passive dam ping control method

1.1.2 加权平均电流有源阻尼方法

基于加权平均电流有源阻尼控制方法的单相并网逆变器系统框图如图3所示.

根据图3，加权平均电流有源阻尼控制方法下，加权平均电流iWAC至逆变器输出侧电压Uab的传递函数可以表示为

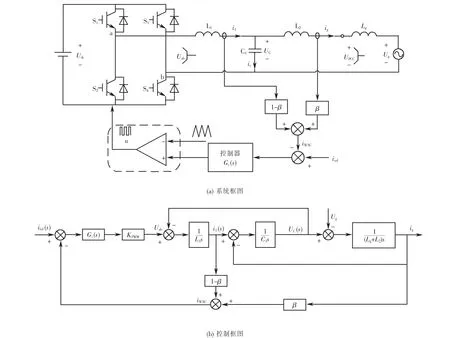
图3 加权平均电流有源阻尼控制方法Fig．3 W eighted average current active damping control method

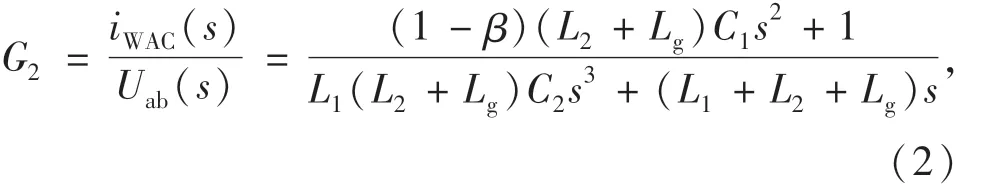
其中：iWAC（s）为s域中的加权平均电流；β为加权系数．

图4为电网阻抗取不同值时，单相并网逆变器系统在加权平均电流有源阻尼下G2的Bode图.从图4可以看出：当电网阻抗取标称值时，系统的谐振峰被完全消除，而当电网阻抗的取值不是标称值时就会出现较大的正向和反向谐振峰，很显然这对于逆变器系统是不利的.

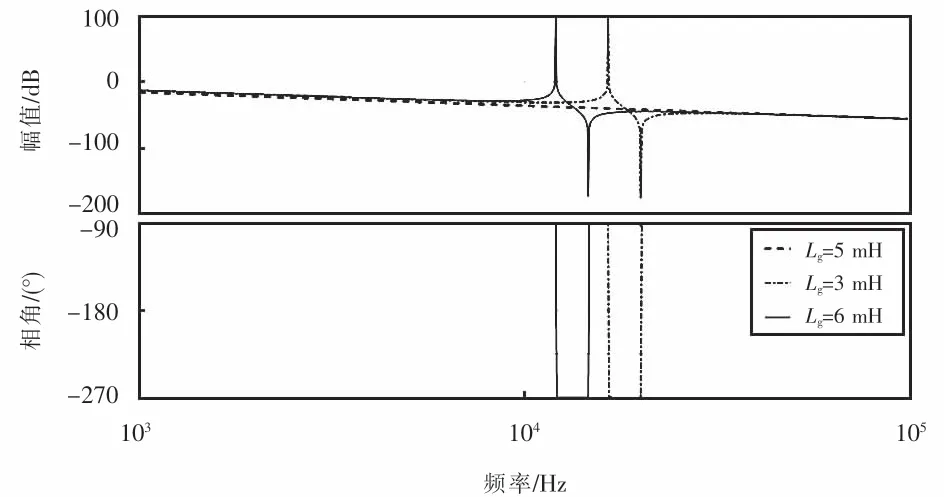
图4 电网阻抗取不同值时系统在加权平均电流有源阻尼控制方法下的Bode图Fig．4 Bode diagram of the system w ith active dam ping control method of weighted average current when the grid impedance takes different values

1.1.3 混合阻尼方法

由1.1.1和1.1.2节的分析可知：无源阻尼方法和基于加权平均电流的有源阻尼方法各有优缺点，因此，考虑将无源阻尼和基于加权平均电流的有源阻尼相结合的混合阻尼方法.基于混合阻尼控制方法的单相并网逆变器系统框图如图5所示.

根据图5，在混合阻尼控制方法下，加权平均电流iWAC至逆变器输出侧电压Uab的传递函数可以表示为

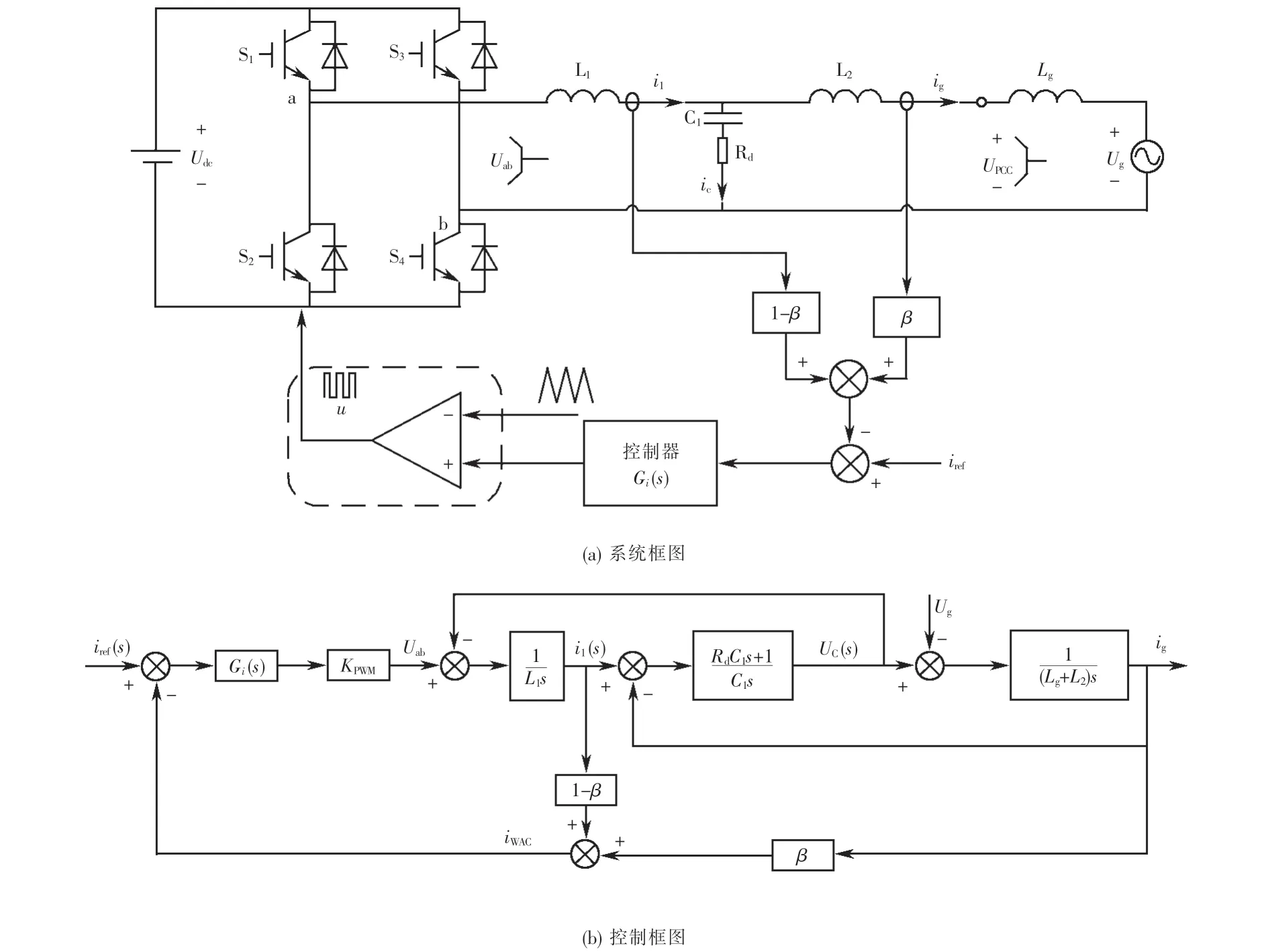
图5 基于加权平均电流的混合阻尼控制方法Fig．5 Hybrid dam ping control m ethod based on weighted average current

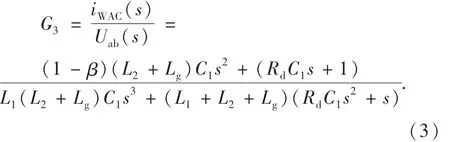
图6为电网阻抗取不同值时，单相并网逆变器系统在混合阻尼控制方法下G3的Bode图.从图6可以看出：当电网阻抗取标称值时，系统的谐振峰被完全消除，而当电网阻抗的取值不是标称值时，相比于加权平均电流有源阻尼的方法明显地抑制了谐振峰，提高了系统的稳定性.

图6 电网阻抗取不同值时系统在混合阻尼控制方法下的Bode图Fig．6 Bode diagram of the system w ith hybrid dam ping control method when the grid impedance takes different values

为了进一步比较3种阻尼方法，绘制出电网阻抗为3 mH时3种阻尼方法下的Bode图，如图7所示.从图7可以观察出：当阻尼电阻Rd取4.8Ω时，无源阻尼的方法可以很好地抑制谐振峰，然而会造成较大的损耗，而采用加权平均电流有源阻尼的方法会出现大的正反向谐振峰，不利于系统稳定.与无源阻尼方法和有源阻尼方法比，混合阻尼方法在较小的阻尼电阻的基础上实现了对谐振峰满意的抑制效果，表现出更优越的性能.

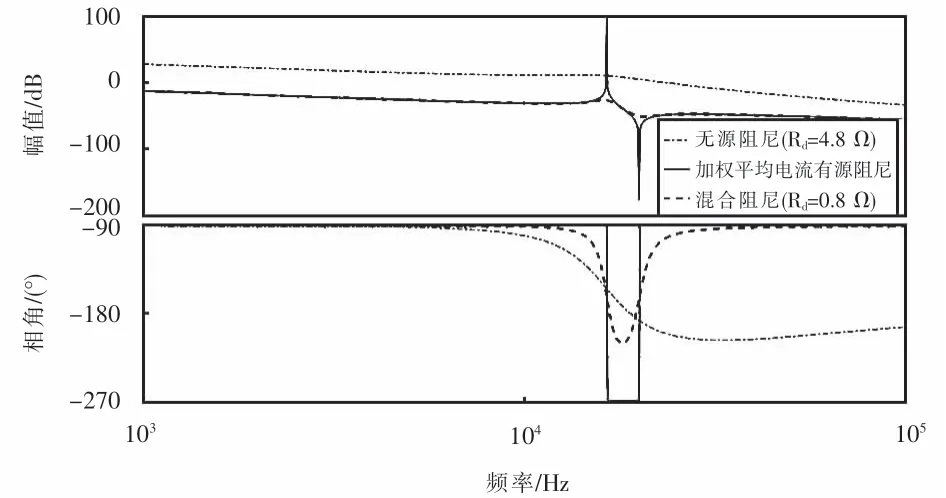
图7 不同阻尼方法下的Bode图Fig．7 Bode diagram under different damping methods

1.2 弱电网下单相并网逆变器系统的建模

1.2.1 标称系统建模

由图8，根据Kirchhoff定律，可得单相并网逆变器系统的电压及电流关系如下：

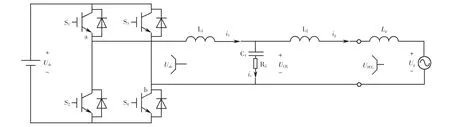
图8 单相并网逆变器系统的拓扑图Fig．8 Topology of single-phase grid-connected inverter system

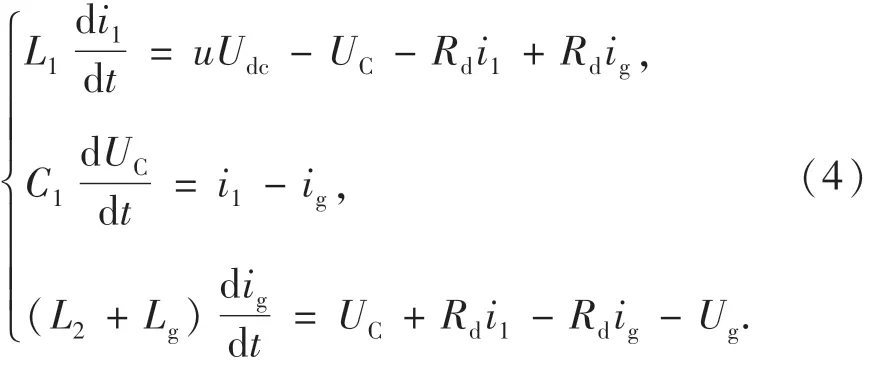
其中：u是逆变器的占空比，同样也是单相并网逆变器系统的控制输入.

选取i1，UC，ig作为系统的状态变量，将系统的数学模型整理为状态空间的形式，如式（5）所示.

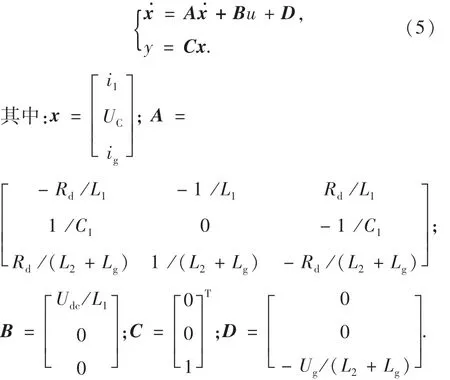
1.2.2 参数不确定系统建模

考虑电网阻抗具有时变特性，同时考虑滤波参数L1，C1，L2摄动和电网阻抗Lg扰动，系统的数学模型可以重新表示为：

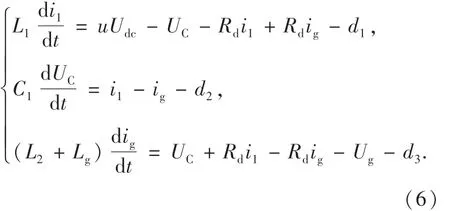
其中：d1，d2，d3表示系统的不确定项．d1，d2，d3表达式如下：

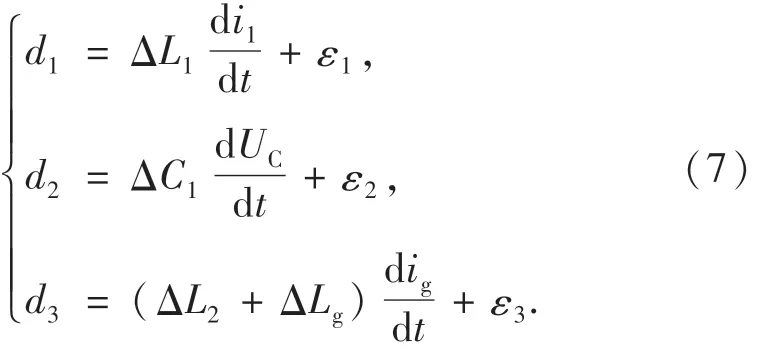
其中：ε1，ε2，ε3表示系统的不可测干扰；ΔL1，ΔC1，ΔL2和ΔLg表示逆变器侧电感值、滤波器电容值、电网侧电感值和电网阻抗值与相应标称值之间的偏差．

2 混合阻尼方法下基于Super-Tw isting的鲁棒电流控制系统设计及稳定性证明

2．1 混合阻尼方法下基于Super-Tw isting的鲁棒电流控制系统设计

图9为混合阻尼方法作用下STSMC的单相并网逆变器系统总控制框图.图9中，并网电流的参考值iref和滤波器电容支路的电压参考值U*CR如下：

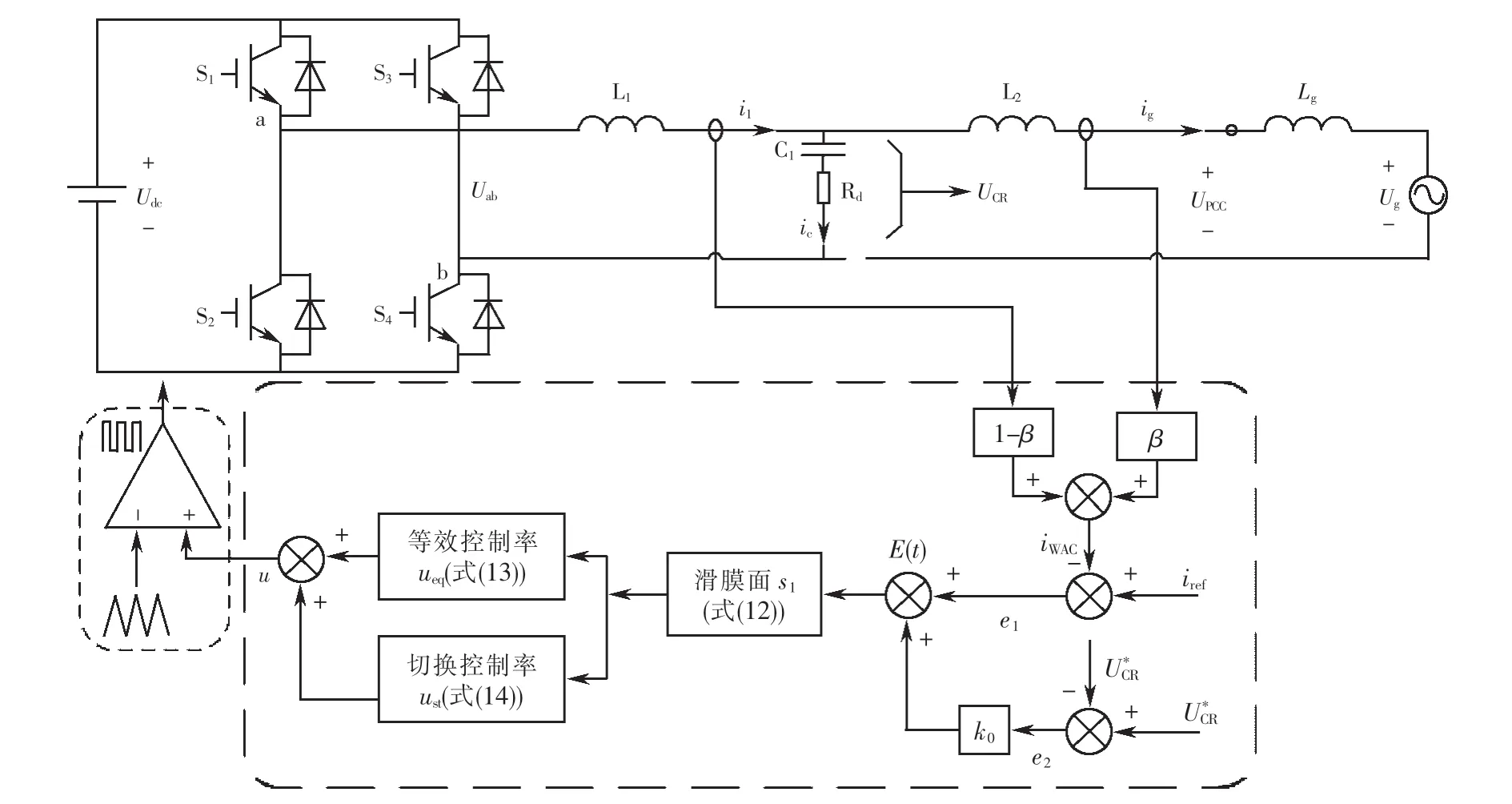
图9 基于STSMC的单相并网逆变器系统总控制框图Fig．9 Total control block diagram of single-phase grid connected inverter system based on STSMC

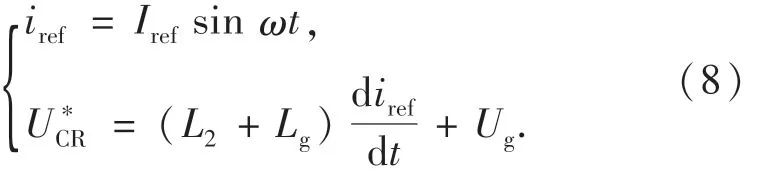
其中：Iref为参考电流的幅值；Ug为理想电网电压，Ug=

加权平均电流有源阻尼方法的加权电流值［11］为

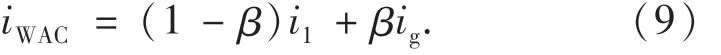
定义单相并网逆变器系统中并网电流的跟踪误差和滤波器电容支路的电压跟踪误差如下：

定义系统误差如下：

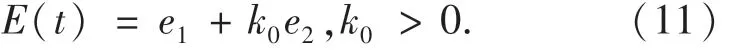
定义系统的滑模面函数如下：

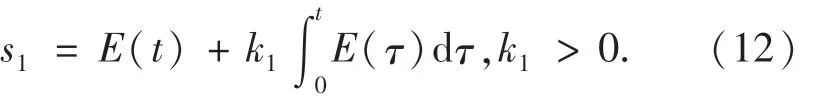
令系统滑模面函数的一阶导数˙s1=0，可得到针对标称系统的等效控制律如下：

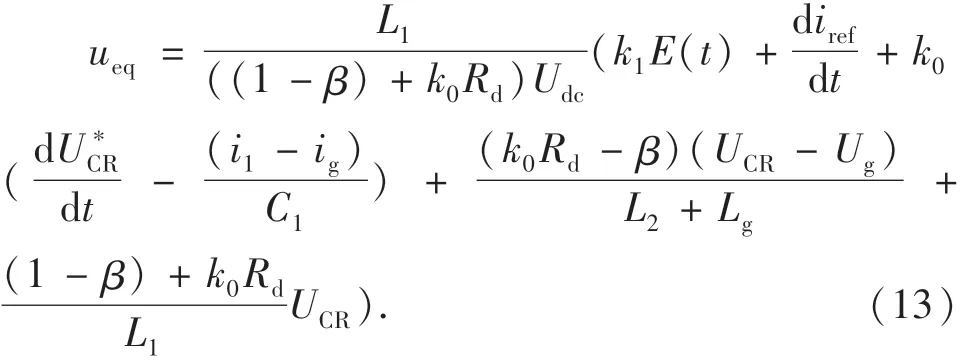
为了消除不确定项对系统的影响，设计基于Super-Twisting的切换控制律如下：

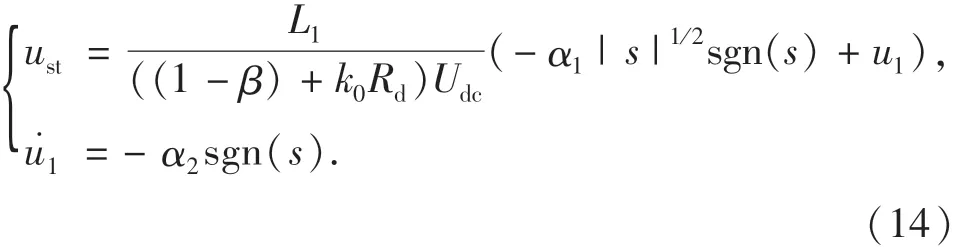
其中：α1和α2为正常数．

结合式（13）～（14），整个系统的控制律如下：

系统的整个控制律是由等效控制律ueq和超扭曲控制律ust两部分组成，其中：等效控制律ueq用于处理标称系统，而超扭曲控制律ust用于处理由于滤波参数摄动和电网阻抗变化等因素产生的不确定项．

2.2 稳定性证明

当考虑滤波参数摄动和电网阻抗变化时，系统的实际滑模面如下：

式（15）控制律是基于理想滑模面设计的，而实际滑模面为式（16），对式（16）求一阶导数，并将式（12）～（15）代入式（16），可得：

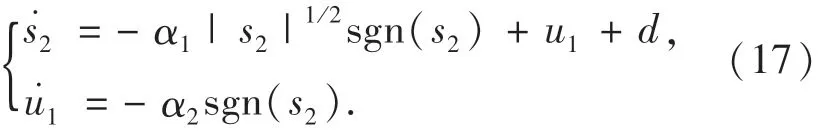
其中：d为系统中存在的总不确定项．d表达式如下：

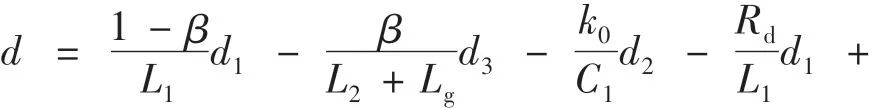
选取系统的Lyapunov函数

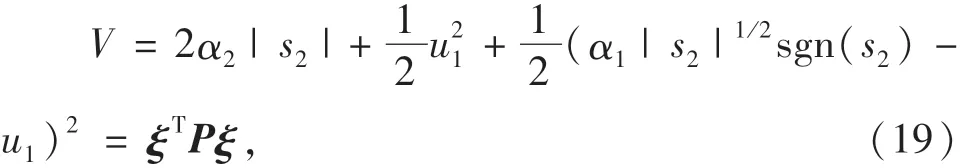
其中：

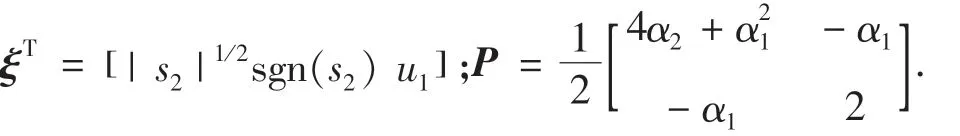
对V求一阶导数，

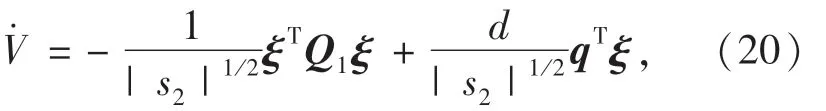
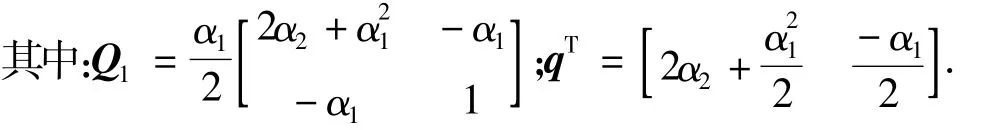
假设

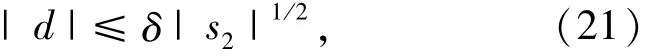
其中：δ为滤波参数摄动和电网阻抗发生扰动时带来的不确定量的边界项．

将式（21）代入式（20）可得

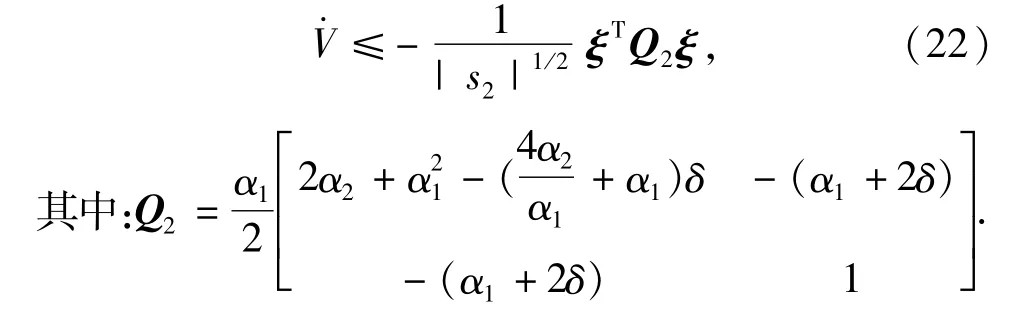
根据Lyapunov稳定性定理可知，V是正定的，只要再满足V·负定就能保证系统是渐进稳定的，因此，可以推出系统稳定的必要条件如下：

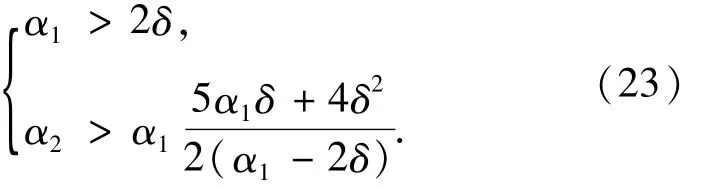
3 仿真结果分析

为了检验混合阻尼下基于Super-Twisting的鲁棒电流控制方法的有效性，利用Matlab／Simulink仿真平台进行验证.本文构造了3种逆变器控制系统进行分析比较：系统1为基于超扭曲滑模控制器的单相并网逆变器控制系统；系统2为基于SMC的单相并网逆变器控制系统；系统3为基于比例谐振（proportional resonance，PR）控制的单相并网逆变器控制系统.仿真时系统用400 V的直流源等效代替分布式电源，逆变器额定容量为3.5 kW.表1列出了系统1进行仿真时的电气及控制参数.

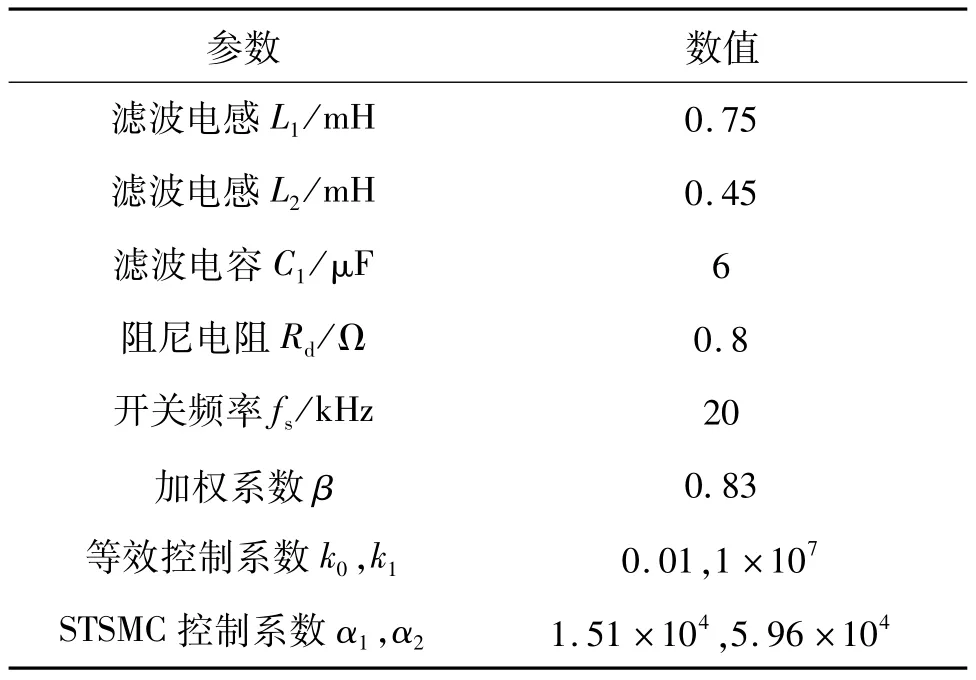
表1 仿真参数Tab．1 Simulation parameters

3.1 系统1、系统2、系统3的动态跟踪性能比较

在0.045 s时将参考电流iref的幅值由10 A设置为15 A，以此来比较所搭建的3个单相并网逆变器系统对并网电流参考值的动态跟踪性能，此时3个系统的并网电流响应波形如图10所示，其中：图10（a）为系统1、系统2和系统3的并网电流跟踪波形；图10（b）为系统1、系统2和系统3的并网电流跟踪误差波形.

从图10（a）中的并网电流动态响应波形可以看出：相比于其它两种控制方法，当参考电流发生阶跃变化时所设计的STSMC方法表现出更快的动态响应能力、更短的调节时间.从图10（b）可以观察出：所设计的STSMC方法表现出更小的跟踪误差、更满意的跟踪性能.

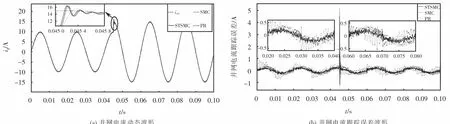
图10 并网电流动态响应Fig．10 Dynam ic response of grid connected current

3.2 系统1、系统2对于滤波器参数变化的鲁棒性比较

为了比较系统1和系统2在滤波参数发生摄动时并网电流的性能，在0.45 s时将逆变器侧电感值从 L1变成1．3L1，滤波器电容值从 C1变成 0．8C1，并且参考电流iref的幅值始终设置为10 A，电网阻抗值取为1 mH.图11为两个系统的并网电流波形图，图12为滤波参数发生变化后2个系统的并网电流总谐波畸变率（total harmonics distortion，THD）.

从图11和图12可以看出：所设计的STSMC和常规SMC对滤波参数发生摄动都能使系统稳定、安全运行，且都具有一定的应对滤波参数变化的能力；然而，与常规SMC相比，当滤波参数发生摄动后，STSMC下的并网电流THD值为0.84%，而常规SMC下并网电流THD值为1.03%，因此，本文所设计的STSMC对于滤波参数的变化鲁棒性更强.

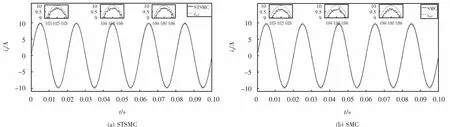
图11 滤波参数摄动时并网电流波形Fig．11 Grid connected current waveform w ith perturbation of filter parameters

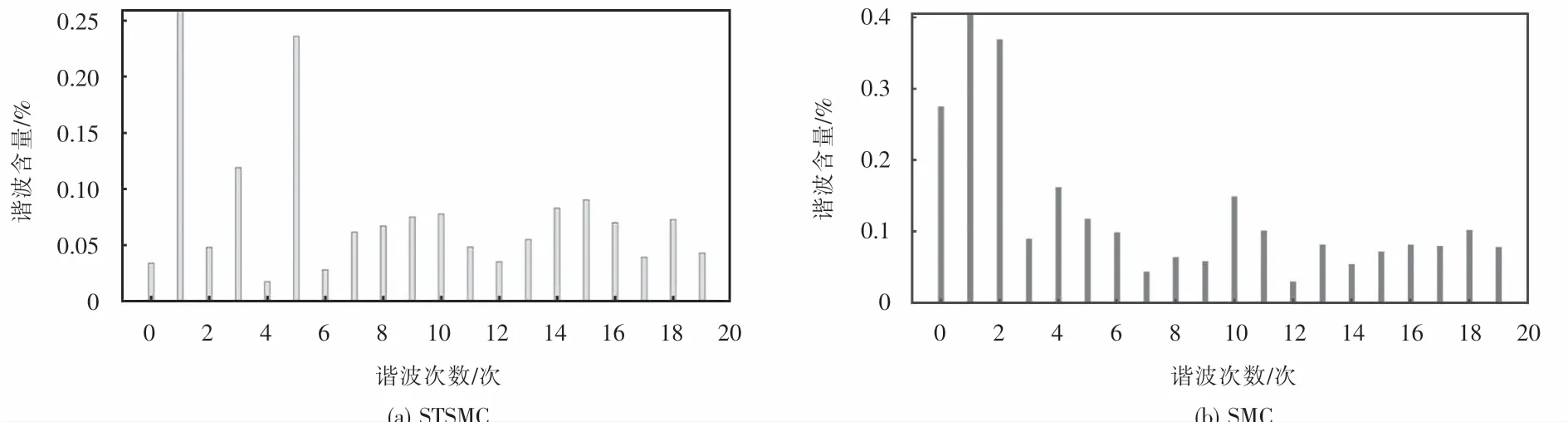
图12 并网电流谐波含量Fig．12 Harmonic distortion of grid connected current

3.3 系统1、系统2对于电网阻抗变化的适应性比较

为了比较系统1和系统2在电网阻抗取不同值时并网电流的质量，在电网阻抗取不同值时对2个系统进行仿真对比.图13～14分别为电网阻抗Lg值为1 mH，5 mH和8 mH时，系统1和系统2的并网点电压和电网电流的波形.表2为电网阻抗取不同值时2个系统并网电流THD值.

从图13～14的并网电流波形和表2中并网电流的THD值的对比可以看出：电网阻抗Lg值分别取1 mH，5 mH和8 mH时，STSMC系统下的并网电流THD值为0.80%，0.57%和0.54%，始终低于SMC系统下并网电流THD值，并且远远低于IEEE.Std519-2014所规定的5%的标准，通过对比能够说明所设计的STSMC可以提高并网逆变器系统对电网阻抗的适 应性，并且能够更好地降低抖振.

表2 电网阻抗取不同值时2个系统并网电流的THDTab．2 Grid connected current THD of two system s when grid im pedance takes different values

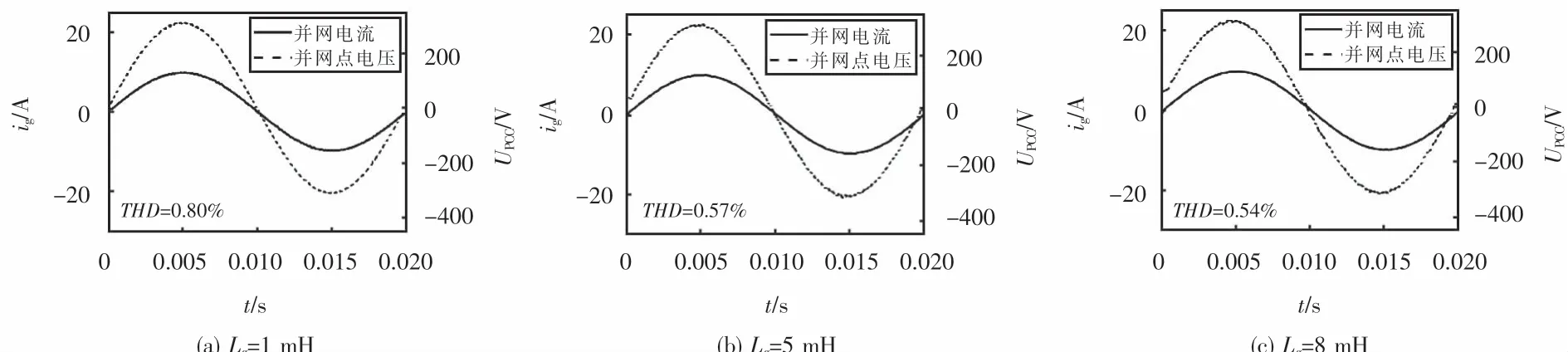
图13 电网阻抗取不同值时系统1的并网电流波形Fig．13 Grid connected current waveform of system 1 when grid impedance takes different values

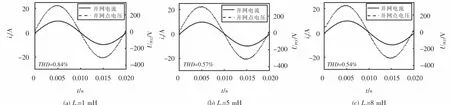
图14 电网阻抗取不同值时系统2的并网电流波形Fig．14 Grid connected current waveform of system 2 when grid impedance takes different values

4 实验结果分析

为了进一步验证所设计方法的优越性，搭建实验平台如图15所示.实验时所用的系统电气参数与仿真时的相同，用于对比实验的系统1、系统2也和仿真实验中相同.实验主要分为两个部分：第一部分通过让滤波参数发生摄动来验证所设计控制方法对波参数变化具有鲁棒性；第二部分通过比较不同电网阻抗时的并网电流波形来验证所设计的方法对电网阻抗的不同取值具有适应性.

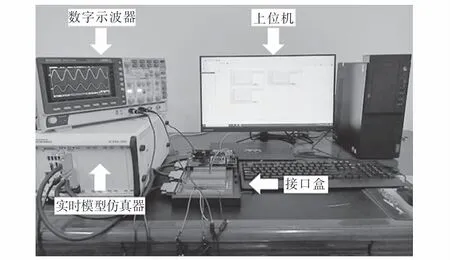
图15 实验平台Fig．15 Experim ental p latform

4.1 系统1、系统2对于滤波器参数变化的鲁棒性比较

当逆变器侧电感值从L1变成1．3L1，滤波器电容值从C1变成0．8C1时，系统1和系统2的并网点电压和并网电流的波形如图16所示.从图16可以看出：实验结果与仿真结果基本一致，2个系统均可以适应滤波参数的摄动，但是对比之下，系统1的并网电流波形质量更好.

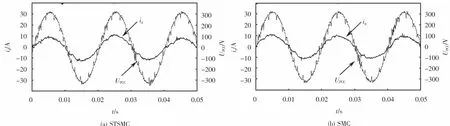
图16 滤波参数摄动时系统并网点电压及并网电流波形Fig．16 Waveform of system grid voltage and grid connected current when filter parameters are perturbed

4.2 系统1、系统2对于电网阻抗的适应性比较

图17 为当电网阻抗Lg取1 mH时，系统1和系统2的并网点电压和并网电流的波形.从图17可以看出：当电网阻抗值偏离标称值较大时，2个系统的并网点电压和并网电流的波形都出现一定程度畸变，但是都能使系统保持稳定，并且相比之下，系统1的波形畸变更小，说明所设计的STSMC对于电网阻抗值偏离标称值时的鲁棒性更强，与仿真分析的结论一致.

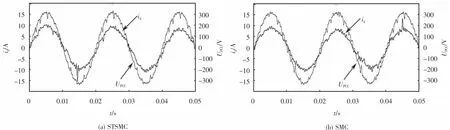
图17 电网阻抗L g＝1 mH时系统并网点电压及并网电流波形Fig．17 W aveform of system grid voltage and grid connected current when grid im pedance L g＝1 m H

5 结论

针对LCL型并网逆变器系统中滤波参数变化和电网阻抗变化等不确定因素会导致并网逆变器系统的并网电流质量下降问题，设计了一种基于Super-Twisting的逆变器控制策略.理论分析表明：所设计的基于混合阻尼方法的STSMC可以提高逆变器系统对于参数变化等不确定因素的鲁棒性，并且通过二阶Super-Twisting控制方法可以削弱常规SMC的固有抖振问题.仿真和实验结果也验证了理论的正确性，进一步说明了所设计的STSMC能够提高逆变器系统在弱电网环境下的鲁棒性，降低对电网阻抗变化的敏感性，得到了更令人满意的并网电流，对工程中的实际应用具有参考意义.