基于边攻击策略的城市交通网络鲁棒性分析

方晟浩，肖 尧，李 平，郭洪鹏

（1.兰州交通大学交通运输学院，兰州 730070；2.中铁第一勘察设计院集团有限公司线路运输院，西安 710043；3.中国铁路设计集团有限公司线路站场枢纽设计研究院，天津 300308）

复杂网络鲁棒性分析是研究在蓄意或随机攻击下网络的抗毁能力与稳定性.目前对鲁棒性的研究主要集中于静态鲁棒性分析与动态鲁棒性分析两个方面.通过移除一部分边或节点分析复杂网络连通性的方法被称为静态鲁棒性分析；通过分析复杂网络中雪崩效应与级联效应的方法被称为动态鲁棒性分析.对复杂网络的攻击方式一般分为蓄意攻击与随机攻击两种，蓄意攻击通过删除复杂网络中重要的节点与边达到攻击目的，随机攻击则是随机挑选节点与边删除以达到攻击目的.

国内外学者对城市交通网络的鲁棒性做了深入的研究，诸多学者提出若干种针对城市交通网络鲁棒性指标的衡量标准，其中，沿用复杂网络领域的分析方法较为主流.强添纲等［1］采用原始映射法构建了包括小汽车网络、地面公交网络和轨道交通网络三者叠加而成的城市多模式交通网络模型.Duan等［2］以三种不同粒度的路网模型：基于分段模型、基于stroke模型和基于社区模型，分别研究了点状、线性和带状交通中断下路网的响应.赵玲等［3］采用基于角度综合的对偶方法进行路网建模处理路网空间数据和计算统计指标，分析其小世界特性、无标度特性以及同配异配性、网络弹性等结构特性.崔文岩等［4］以负载重分配动力学过程有重要影响的节点度和介数两种指标作为构建依据，提出一种节点度和介数相关边权的网络级联抗毁性模型.冯霞等［5］将中国航空网络建模成无向加权复杂网络，在分析航空网络拓扑结构特性的基础上，研究分析了航空网络的鲁棒性.王尔申等［6］提出了基于边攻击成本的复杂网络鲁棒性研究方法，通过将边的攻击成本因素考虑在内，结合两种人工合成网络和四种真实网络对每个网络的鲁棒性进行了深入研究.Hong等［7］提出了一种改进鲁棒性指标R的计算效率的方法，即当失效节点的值达到临界阈值qc时，引入一种计算效率较高的鲁棒性测度R′.Holme等［8］对现有的几种复杂网络模型以及科学协作和互联网的现实网络进行了数值研究，并用最大连通子图的大小来定量测量网络性能.田晶等［9］基于大样本城市道路网的鲁棒性及受不同鲁棒性模型、不同攻击测量的影响作出分析.金成菲等［10］为了评价公共交通在高峰时段的运行状态，研究交通拥堵影响下公交网络的鲁棒性.基于Python技术，获取平台分析车辆出行大数据得出的拥堵指数，以拥堵指数作为权值，构建了公交线网无向加权的复杂网络.雷永霞等［11］针对我国高速铁路客运专线运输网络受到站点攻击时边权值对网络鲁棒性的影响，依据复杂网络理论，利用Pajek软件建立了高速铁路客运专线无向加权运输网络模型，利用Matlab分析了该网络模型在随机站点攻击和蓄意站点攻击下的连通鲁棒性和功能鲁棒性评价指标.

鲁棒性分析是通过对复杂网络中的节点进行攻击达到的，城市交通网络通过原图法（primal approach，PA）所组成的复杂网络中，节点代表道路交叉口，边表示城市道路.本文在传统的攻击节点方法的基础上，提出了结合复合边权重的对边攻击策略模型，该模型既体现了路口在整体城市交通网络中的连接度，同时顾及最短路径通过每条道路的次数，在城市交通网络的鲁棒性分析中更贴合实际，并最大限度的保留了城市交通网络的布局特点.

1 网络研究方法

1.1 复杂网络基本属性

构建网络模型之前对复杂网络的基本属性进行介绍，以便后文分析使用.

1）网络的平均路径长度也被称为网络的特征路径长度，用来界定一个网络中所有节点对之间的最短路径的平均长度，可通过公式表达为：

式中：n为节点总数；dij为节点i与节点j间的最短路径长度．i，j∈ n，n=1，2，…，n．

2）加权网络效率是指加权网络在被攻击导致本身的构成发生了变化后对最短路径产生的影响，在计算最短路径时应考虑两点间最短路径所涉及的边的权重，若两点间不存在最短路径则将长度表示为无穷大，两个节点之间的效率通过计算两点间最短路径长度的倒数表示，加权网络效率则通过计算所有节点之间效率的平均值得出，可通过公式表达为：

3）节点介数代表网络中所有经过某节点的最短路径数占最短路径总数的比例，节点介数的提出弥补了节点度对于节点在网络中重要性描述不够精确的问题，反映了该节点在网络中的重要性，可通过公式表达为：

式中：njk为节点 j、k之间最短路径的总数；njk（i）为经过节点i的j、k间最短路径的数量．

4）最大连通子图（maximal connected subgraph，MCS）表示把网络中所有节点用最少的边将其连接起来的子图，因其具有不唯一性所以也可称为极大连通子图.通常作为判断网络的连通性的指标［12-15］.

1.2 网络模型构建方法

城市交通网络根据其拓扑特性抽象为网络模型的方法有两种：原图法和对偶法（dual approach，DA）.原图法是一种将城市道路之间的交叉抽象为网络中的节点，将交叉间的路段抽象为连接节点的边的建模方法；对偶法一般指原图法的对偶，是一种将城市的道路抽象为网络中的节点，将城市道路间的相连关系抽象为连接节点的边的建模方法.

在实际应用过程中，上述两种网络模型构建方法各有优劣.原图法构建的网络最大限度的保留了城市交通网络的布局特点，能够精确的表现城市交通网络的地理布局，但是在表达道路之间潜在的连接关系上不够明确.对偶法构建的网络将道路间的连接关系表达得十分清楚，但是忽略了城市交通网络的空间特性导致这种方法丧失了直观性.在两种方法的比对权衡后，本文选用原图法进行网络的构建与分析.

1.3 边加权方法

现实世界中大部分网络都是加权网络，网络中边的权重通常表示这条边的承载能力或与节点间的联系程度．可以用V=（N，W）描述加权网络，其中N为节点数，W为边的权重，可构建其加权邻接矩阵W =（wij）n*n，其中 i，j=1，2，…，N．

目前定义边权重的主流方法有两种，分别是节点度法及节点介数法．其中节点度法的主要思路是将与边相连的两个节点的度k相乘以得到边权重，可通过公式表达为：

介数法则是通过与边相连的两个节点的介数相乘得到的，这种方法的优点是能够更准确的反应边在网络中的重要程度，可通过公式表达为：

再结合式（4）与式（5）综合考虑节点的度与介数后可得出复合边权重的计算可通过公式表达为：

式中：θ为可调的权重参数，文献［4-7］中总结出当θ≅1时临界阈值最小；α为比重系数，0≤α≤1，当α=0表示边的权重仅与节点的度相关，当α=1表示边的权重仅与节点的介数相关．

2 实验及分析

2.1 网络数据及构建

在实验中本文选用2019年8月天津市中心路段交通地图构建城市交通网络，以ArcGIS10.8作为空间数据的采集平台，首先提取可编辑的路网数据，经过拓扑检查处理悬挂点、伪结点、孤立路段与冗余路段，得到一个包含366个道路交叉口与703个路段的天津市中心路网图，随后通过原图法将每个道路交叉口抽象为节点，路段抽象为边，得到相应的路网图与连接图如图1所示.

图1 天津市中心路网图及其拓扑关系图Fig．1 Tianjin center road network and its topological relationship

2.2 计算分析网络特征值

根据连接图，结合Python编写特征值计算程序可得该网络的最大度、最小度、密度与平均度，并分别采用式（1）、式（2）得到该路网的群聚系数与平均路径长度如表1所列.

表1 网络特征值计算结果Tab．1 Calculation results of network eigenvalues

2.3 计算边权重

首先以节点度法对天津市中心路网中所包含的703条边进行加权，将网络中所有节点进行编号，计算构成一条边的两个节点a与b各自的度并结合式（4）进行相乘处理，而后将所得结果归一化处理得到边的节点度权重，部分结果如表2所列.

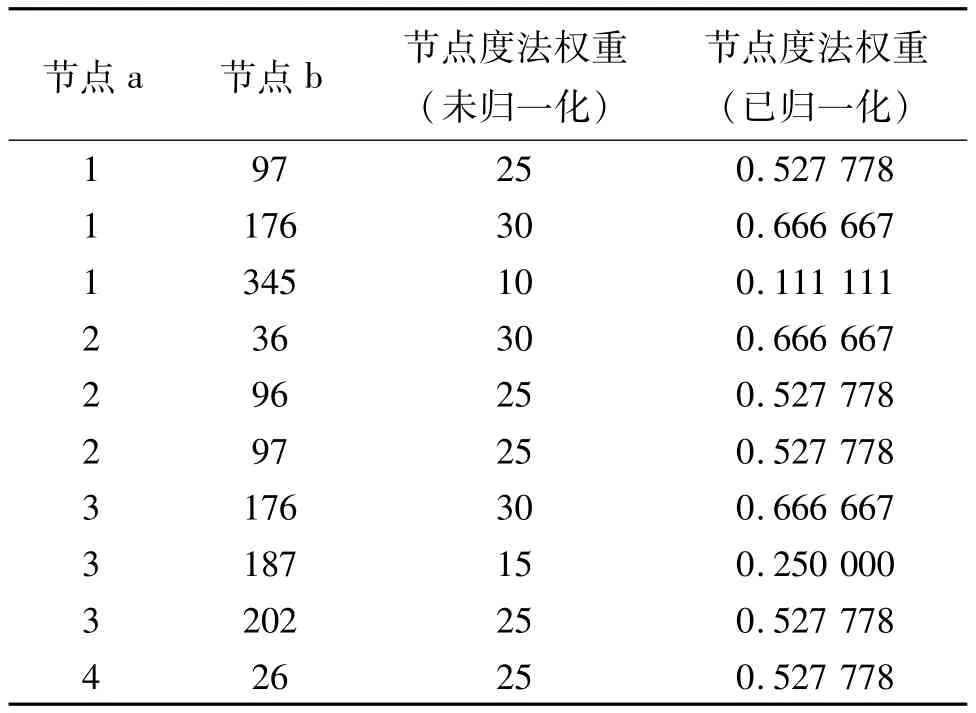
表2 节点度法权重计算结果Tab．2 Node degree method weight calculation result

其次以介数法对网络中的边加权，计算构成一条边的两个节点各自的介数并结合式（5）进行相乘处理，随后将所得结果归一化处理得到边的介数权重，部分结果如表3所列.

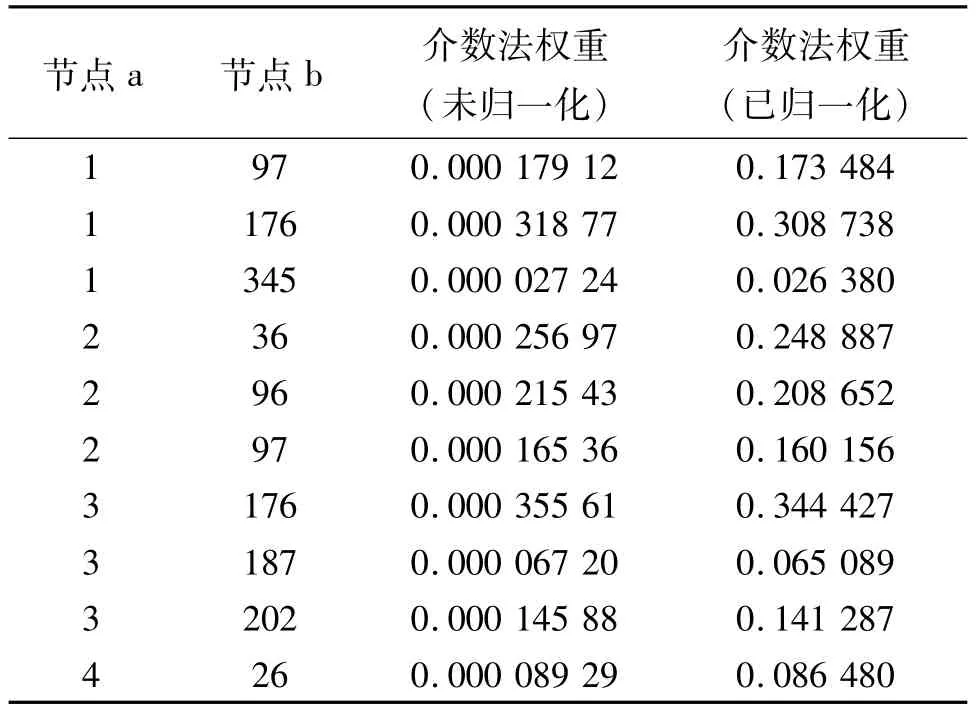
表3 介数法权重计算结果Tab．3 Calculation result of betweenness method weight

最后以复合权重法对网络中的边加权，结合式（6）对节点度法权重与介数法权重进行计算，取α=0．3，θ=1，得到边的复合权重如表4所列.

表4 复合法权重计算结果Tab．4 Com pound method weight calculation result

2.4 鲁棒性分析

鲁棒性（robustness）由其英文音译而来，也可称为抗毁性、稳健性、强健性，是系统的抗毁能力，它是在异常和危险情况下系统生存的关键，是指系统在一定的攻击策略下，维持某些性能的特性.本文采用网络效率与文献［15-17］提出的通过最大联通子图衡量攻击后网络性能的方法.

本文通过最大连通子图的相对大小S作为衡量网络连通鲁棒性的评价标准，其计算公式如下：

式中：N为未遭受攻击时网络中的初始节点总数；M为该网络遭受攻击后最大连通子图中所包含的节点数．

本文采用随机攻击策略、基于度权重的边攻击策略、基于介数权重的边攻击策略与基于复合权重的边攻击策略四种方法对天津市中心路网进行攻击以分析其鲁棒性.

图2给出了天津市中心城区交通网中边分别受到随机攻击与蓄意攻击（度攻击、介数攻击与复合攻击）后，最大联通子图相对大小S的变化，图中的横坐标f表示网络的损毁程度，即在网络中受到攻击的边数与初始网络中总边数的比值.随着网络中被攻击的边的数量增加，逐渐出现了被孤立的节点，导致网络的最大连通子图的规模不断的缩减直至网络崩溃.分析图2可知，在随机攻击的策略下，当网络的损毁程度接近1时，最大连通子图的相对大小才接近于0；在度攻击策略下，网络的损毁程度接近0.8时，最大连通子图的相对大小接近0；而在介数攻击与复合攻击策略下，网络损毁程度接近0.7时，最大连通子图的相对大小接近0.同时在边损毁至35%时，在介数攻击策略下网络最大连通子图的相对大小呈断崖式下降；而在边损毁至40%时，在度攻击策略下网络最大连通子图的相对大小呈断崖式下降，如图2所示.

图2 最大连通子图与边删除比例关系图Fig．2 Ratio of the largest connected subgraph to the removed edges

图3 给出了天津市中心城区交通网中边分别受到随机攻击与蓄意攻击（度攻击、介数攻击与复合攻击）后，加权网络效率Ew的变化.网络在初始状态时，加权网络效率为0.13，在随机攻击的策略下，当网络的损毁程度接近1时，加权网络效率才接近于0；在蓄意攻击的策略下，当网络的损毁程度接近0.8时，加权网络效率接近于0，如图3所示.

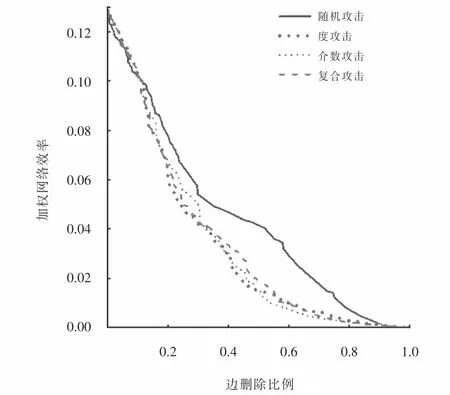
图3 加权网络效率与边删除比例关系图Fig．3 Scale of weighted network efficiency vs．removed edges

上述分析可得，网络在蓄意攻击下鲁棒性明显变弱，同时在网络损毁至不同阶段时，度攻击策略与介数攻击策略都会使网络最大连通子图的相对大小呈现断崖式下降.在单个边受到攻击时，整体网络的鲁棒性变化并不明显.

3 结论

本文将天津市中心城区交通网络抽象建模成无向加权复杂网络，通过拓扑结构特性研究分析其鲁棒性.利用本文涉及的多种边攻击策略，经计算分析可得出如下结论：

1）在大部分边受到随机攻击从而导致失效时，天津市中心城区交通网络仍可以保持相对稳定的连接，鲁棒性较为优秀，然而在蓄意攻击策略下，当受到攻击的边达到60%～80%时整个网络便会崩溃瘫痪.同时，部分权重较大的边对网络的整体连通性起到至关重要的作用，这些道路失效会使网络的连通性急速下降.

2）加权边介数攻击与加权度攻击对网络的破坏性较强，且复合权重攻击策略可以兼顾上述两种蓄意攻击的模式.

3）通过对造成网络连通性断崖式下降的边进行分析与识别，发现天津市中心干道（如南京路、卫津路等）的鲁棒性明显较差，应对关键道路采取有效的防护措施并及时进行日常维护，降低突发灾害事件对城市交通网络连通性的影响从而降低损失.

本文只考虑了结合复合权重边的攻击策略，如何结合复杂网络的动力学并考虑网络的级联失效性以及其他因素对网络鲁棒性的影响，还有待进一步的研究.