基于超节点协同一致性算法的分布式电源经济调度策略研究

李 红，董海鹰

（兰州交通大学自动化与电气工程学院，兰州 730070）

近年来，随着能源互联网的发展，风力、光伏等分布式能源数量增加，需要协调的电源节点数也急剧增长，传统的电网结构和电源调度模式受到了严重的挑战.分布式电源的优化调度是主动配电网安全稳定运行的重要保障，而分布式电源的优化调度方式则主要为集中式调度和分布式调度［1-2］.

在集中式调度控制中，主要通过调度中心获取全网的海量数据，用于对整个网络中各节点的运行状况检测和控制.该方式导致计算时间长、通信延时，同时还影响计算结果的准确性，一旦某个节点或电源发生故障，就会导致全网的用电质量降低或故障，可扩展性差，无法满足智能电网的即插即用需求；另外，集中式经济调度算法隐私保护性方面也较差［3］.

分布式经济调度控制强调参与调度各单元的自主决策和个体智能，通过多个单元的协同配合实现经济调度目标，能够避免集中式优化算法的上述不足.文献［4］提出了一种基于一致性算法的自适应下垂控制策略，用于解决传统下垂控制中频率、电压偏差、系统稳定性和功率分配精度的问题.文献［5］利用配电网中各节点电价函数，通过一致性算法来调节电力系统中燃气轮机的微增率，使其达到一致性，实现经济成本最优，同时也已经涉及到了分布式电源在电力系统中的调节作用.文献［6］提出了一种基于离散一致性算法的分布式储能系统负荷功率分配分层控制策略，多点配置储能系统，相互之间建立通信机制，以等效荷电状态为一致性目标，实现了对分布式储能系统输出的动态调整.文献［7］则以储能系统的经济运行为主要目标，利用储能修正增量成本作为一致性因子来优化其功率输出.文献［8-10］采用一致性算法实现储能间和分布式电源的经济分配.上述文献主要通过建立一致性算法来解决传统能源和分布式电源的运行成本经济性，但并没有考虑其建立的通信机制下一致性算法的收敛速度.

和集中式控制策略不同，分布式控制策略中每个单元需要进行相互迭代以优化被控量的参考值，其收敛速度的提高可以进一步提高系统的稳定性［11］.文献［12］采用事件触发控制策略实现组合连通拓扑结构下的平均一致性.文献［13］一致性算法的收敛系数是选取拓扑图的拉普拉斯矩阵的最大特征值的倒数，实现了渐近时间平均一致性.文献［14］一致性算法的收敛系数是选取拓扑图的拉普拉斯矩阵的所有不同非0特征值的倒数，这种算法实现了有限时间平均一致性.文献［15］通过对原有拓扑图中节点的区域局部划分，以及局部集之间选取超节点进行通信来提高多智能体平均一致性算法的收敛速度.文献［16-20］则是通过对通信拓扑或者权重系数的优化来提高一致性算法的收敛速度，以分布式电源的经济运行成本趋于一致为目标，实现了对其输出的优化.目前电力系统中分布式电源的投资者有可能不同，分布式电源的经济成本虽然降低，但是有可能会破坏投资者之间的利益平衡.

本文针对一致性算法的收敛速度，提出基于超节点协同的分布式电源一致性调度算法.利用图信号处理和智能体一致性算法的关系，将分布式电源在原有拓扑图的基础上进行超节点的选取和局部集的有效划分；以系统中每台分布式电源最大容量与其输出容量比例分配为一致性目标，在优化投资者之间收益均衡的同时，有效提高一致性算法的收敛速度.

1 离散一致性算法

1.1 图论基础

在图论中，节点之间的网络拓扑结构可以用无向图G=（V，E）来表示，其中：V∈Rn为节点的集合，n为节点总数；E为边的集合．与节点相连的边的条数称为该节点的度，对角度矩阵用D表示，D∈Rn×n；邻接矩阵A表示网络中节点的连接关系，若相邻两节点i与j相连，则元素aij=1，否则aij=0，易知A∈Rn×n，且主对角元素为 0．

取拓扑图的拉普拉斯矩阵L ＝D-A，则L∈Rn×n，且为半正定的对称矩阵，因此可以将L继续分解为L＝YΛYT，其中：Y为L的特征向量；Λ为对应的特征值矩阵，Λ =diag（λ1，λ2，…，λn）．对特征值按大小进行排列，得

可以证明［20］，在多节点组成的无向连通图G中，如果G是连通的，则λ2＞0．

1．2 一阶离散一致性算法

在对系统建立好对应的通信拓扑图后，可以利用一致性协议来实现图中各节点信息的更新迭代，使各节点输出信息体现一致性原则，在离散时间的情况下，系统中各节点之间的状态空间表达式可以表示为

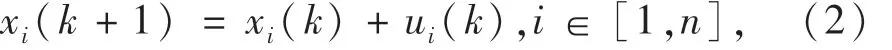
其中：xi（k）表示第i个节点当前时刻的状态信息输出值；ui（k）表示当前时刻节点i的当前控制输入信息．为了使所有节点达到一致性协议，可以将ui（k）表示为

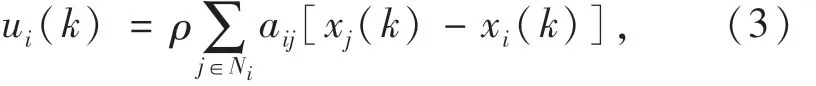
其中：ρ表示当前时刻节点i的控制权重，用于控制系统收敛的速度．当系统中节点趋于稳定时，对应的稳态解为

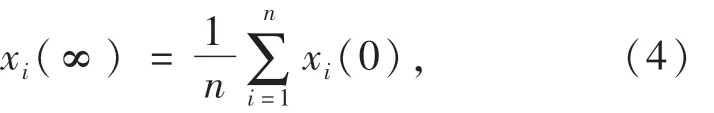
即系统中所有节点在趋于稳态解时，系统将会实现平均一致性．将系统的空间表达式写为矩阵形式，

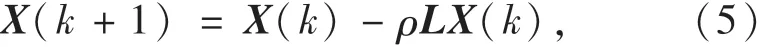
其中：X（k） =［x1（k），x2（k），…，xn（k）］T．因为 L的对称半正定性，可以继续将式（5）表示为

利用图论知识可知，在对图信号处理时，可以利用函数m=f（L）m′对其进行滤波，其中：m′和m分别为滤波前后的信号值向量，因此，可以将式（6）中节点之间的协同过程看作是信息更新滤波的过程，X（k）和X（k+1）看作滤波前后的节点输出信息状态变量，而滤波器函数则可以表示为

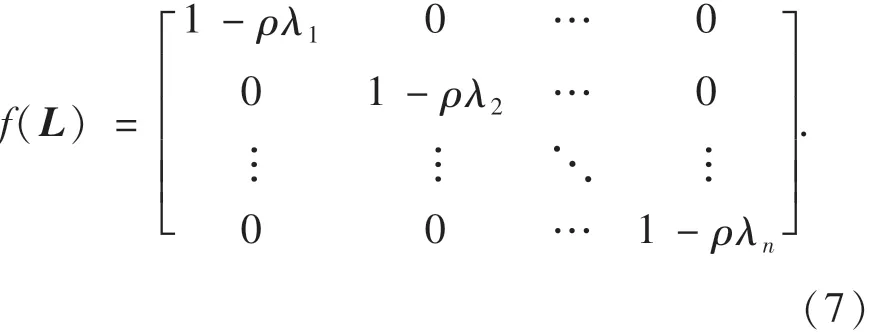
可以看出：在对系统中节点建立通信拓扑后，式（7）中的变量仅有ρ，因此，对协同控制系统中控制输入的设计，可以被看作是对ρ的设计问题．可以证明［21］：当ρ的取值为L的最大特征值的倒数时，系统中各节点之间的输出值是渐进时间收敛的，同时该方法的优势在于，只需要获取通信拓扑图对应的L的最大特征值λmax即可，具有很好的鲁棒性和工程应用价值．

1.3 超节点协同一致性

系统中各节点之间建立通信之后，可以利用一致性协同算法来实现各节点处均衡，但是，当系统随着系统中节点数越来越多时，因为其复杂的通信机制，将会降低整个系统的收敛速度，此时可以在建立好的通信拓扑图中通过提取超节点来解决这一问题.具有超节点的拓扑结构如图1所示.

图1 具有超节点的拓扑结构示意图Fig．1 Schematic diagram of topology w ith super nodes

由图1可知，可以在建立好的初始通信拓扑中提取合适节点作为超节点，超节点之间再次建立通信拓扑，对原有拓扑图进行降维和重建，完成图的粗化.具体为：首先，获取初始通信网络拓扑结构，找到度di最大的节点作为超节点，利用该超节点与其邻接节点构成局部集，局部集内部节点与局部集外节点通信需要打断，剩余部分组成新的图；然后，在剩余图中继续按照上述方法寻找超节点，直到所有节点都被划分到对应的局部集为止．在划分局部集后，若局部集内部节点在初始通信拓扑中与其他局部集节点有通信连接，则需要使用超节点来代替该连接，以达到局部集之间相互联系的目的；然后，利用局部集内部的超节点组成粗化图Gc，从而完成对原始图的降维与重建，具体流程如图2所示.

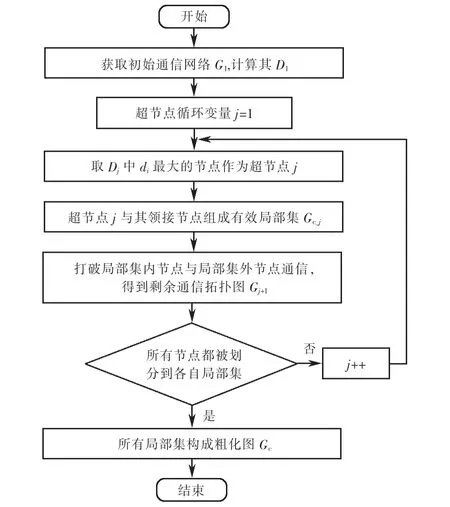
图2 基于超节点选取的流程图Fig．2 Flow chart based on super nodes selection

基于超节点协同的一致性算法仍以式（3）为基础，首先利用超节点构成的粗化图进行一致性算法协同控制，粗化图达到协同一致性之后，局部集内部再利用其通信机制进行一致性协同控制，以此实现整个系统分布式协同控制.

2 配电网中分布式电源建模

配电网主要由光伏和风电等分布式电源、储能和负载组成，具体的配电网简化结构如图3所示.图3中，PrefPCC和QrefPCC分别表示调度中心在PCC（point of common coupling，公共连接点）处的有功和无功指令参考值.

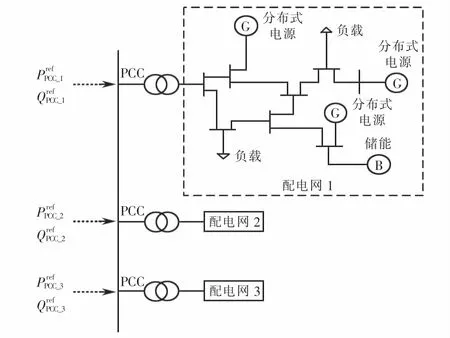
图3 配电网简化结构示意图Fig．3 Simplified structure diagram of distribution network

目前随着分布式电源接入配电网，造成了配电网潮流变化的不确定性，因此，可以通过对分布式电源的协同调度，实现对调度中心给出的P，Q参考值进行跟踪，优化配电网的调度能力．此时，原本复杂的电力系统优化问题将会变成对配电网单纯的P，Q控制问题，而在负载不变的情况下，PCC的P，Q优化主要通过对分布式电源和储能系统的控制来实现.

分布式电源和储能系统的基本结构可以用基本的变流器来表示，具体的含有控制结构的变流器示意图如图4所示.该分布式电源由一个典型的三相变流器组成，可再生能源（renewable energy sources，RES）在变流器直流侧进行供电.控制系统测量PPC处电压vPCC、变流器网侧电流i2和LCL滤波器中电容电流ic，并将其转换为在两相静止坐标系下用于对变流器的控制，使其输出特定的功率.

图4 变流器基本结构示意图Fig．4 Basic structure diagram of converter

变流器使用PCC功率控制层、协同控制层和物理控制层来实现分层控制策略.其中：功率控制层的KP和 KQ为比例控制因子；μP和 μQ为功率补偿调节因子．当需要补偿的有功功率在0和Pmax-i之间时，μP为常数，反之μP=0；当补偿无功之前，节点电压在 Umin和 Umax之间时，μQ为常数，反之 μQ=0.功率控制层接收中央调度系统下PCC处的总功率指令；协同控制层接收邻居节点变流器的功率信息，用于对分布式电源出力和储能SOC（state of charge，荷电状态）值进行协同控制；物理控制层则被用来控制变流器工作.

针对图4中分布式电源的基本结构，可以对分布式电源建立通信拓扑，并在通信拓扑的基础上利用协同控制算法，使分布式电源系统内部协同工作.

3 基于超节点的分布式电源的协同控制

对分布式电源功率输出进行协同分配是为了满足针对不同设备投资者间的收益分配，促进电力市场和谐发展［22-24］.相同的电网中，分布式电源的投资者可能不同，另外，实际工况中，当分布式电源不支持满负荷运转时，根据配置在该电网中分布式电源容量，可按比例分配其输出量，从而可以很好地对设备投资者的收益进行分配，即对分布式电源输出进行协同控制之后，达到其最大容量与输出量比例的一致性.

对分布式电源进行协同控制是在PCC功率守恒的前提下进行的，因此，分布式电源和储能在PCC的注入功率要时刻跟随调度中心要求的参考值，即：

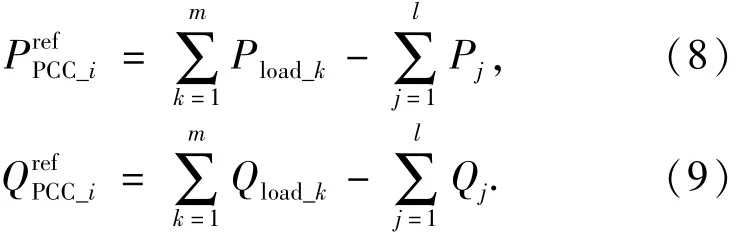
其中：Pj和Qj分别表示PCC处分布式电源或者储能产生的有功功率和无功功率；Pload-k和Qload-k分别表示负荷消耗的有功和无功功率．

在对分布式电源的有功协同控制时，考虑到设备的收益与发电量相关，因此，为了均衡每个分布式电源之间的收益，利用一致性算法对分布式电源的有功输出进行系统控制，按照分布式电源的容量对其发电量按比例进行分配．采用分布式电源的最大输出容量与实际输出容量的比值λP-i作为一致性因子，因此，分布式电源中针对有功分配的分布式一致性算法设计实现如下：

其中：ρP表示有功协同控制权重；Pmax-i表示第i个分布式电源或储能的最大输出有功量；Pct-i表示对应分布式电源的协同控制有功量．因为针对多个分布式电源的有功进行协同分配时，使用的通信拓扑图为无向图，因此，对应的L矩阵满足1TL=0［21］．根据式（11）可得

这也从理论上证明了上述分配协同控制算法在迭代的过程中，如果有功总需求不变，则供需平衡就不会被打破．

对分布式电源来说，不仅仅需要对配电网提供有功功率，还需要对配电网输出无功功率，以此来承担配电网的电压调度．假设i，j两个节点的电压为Ui∠0和 Uj∠δj，同时两点之间的阻抗为 Zij∠θij，则可以写出i点的潮流方程如下：

在确定无功与分布式电源接入点的电压关系之后，可以继续利用分布式一致性算法对电压进行均衡，采用电源与配电网连接点的电压有效值的归一化值λQ-i作为一致性因子，对应的算法设计如下：

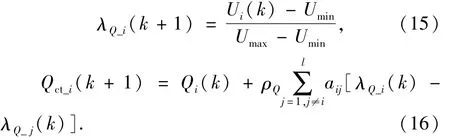
其中：ρQ表示无功控制权重；Umin和Umax分别为节点i处的电压最小允许值和最大允许值；Qct-i表示对应分布式电源的协同控制无功量．当需要补偿的无功超过容量极限值时，该分布式电源不再承担电压均衡的工作，同时此时以容量最大值进行输出．同样，针对无功的协同分配时，使用了和有功分配相同的通信拓扑，因此，也可以根据式（16）得出相应的无功供需结论：

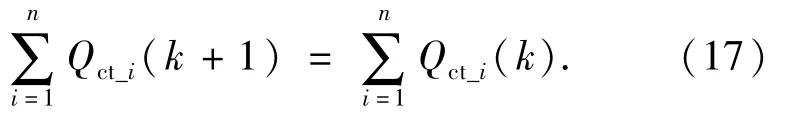
因此，多个分布式电源在进行无功协同分配时，在迭代过程中只要总的功率需求不发生变化，对应的供需平衡也不会被打破．

对于储能系统来讲，主要通过充放电与PCC进行能量的交互，在本文的设计中，使用储能参与分布式电源的有功与无功分配，同时在储能系统工作时，为了防止对应SOC越限，可以在图3所示结构的协同控制层上继续引入SOC恢复机制，具体的控制信号如下：

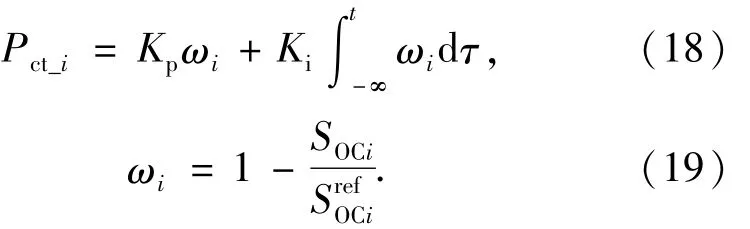
其中：Kp和Ki分别为PI控制器的比例调节系数和积分调节系数；ωi为输入PI控制器的误差值；SOCi为储能荷电状态实际值，SrefOCi为对应的参考值．

在建立普通的通信拓扑对分布式电源和储能系统进行分布式协同控制之后，为提高整个系统的算法的收敛速度，继续采用超节点对节点进行划分.

4 仿真验证

为了对本文提出的算法有效性进行验证，搭建一个14节点的小型辐射状配电网（见图5），并在该配电网中标序号处配置图4所示结构的变流器.本次仿真是为了验证基于超节点的一致性算法有效性，假设变流器可以实时跟随其参考值对电网进行功率补偿，即不需要变流器配置物理控制参数.

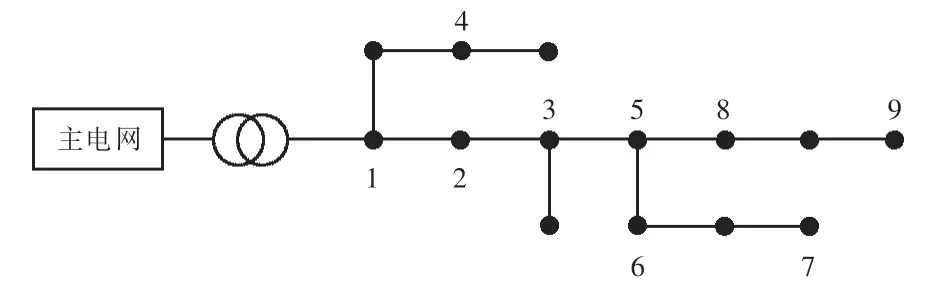
图5 简化的14节点配电系统Fig．5 Simplified 14 nodes distribution system

对分布式电源建立的基本通信拓扑图见图6，另外，主电网利用广播的形式将功率信息传递给分布式电源，分布式电源之间利用图6所示的通信拓扑进行功率信息交互.

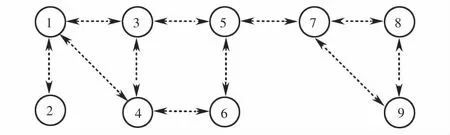
图6 分布式电源节点通信拓扑图Fig．6 Communication topology of distributed generation node

参与功率分配的分布式电源有功输出最大值分别为80，40，60，30，50，40，60，80和 30 kW.配电网的额定相电压为220 V，允许波动范围为5%.初始状态下在经过主电网对配电网功率注入后，配电网系统还需要分布式电源补偿206 kW 有功功率和50 kvar无功功率.本次仿真针对分布式电源的有功分配分为4个阶段：0～2 s之间分布式电源依靠通信系统对初始状态下需要分配的有功进行协同分配；2～3 s之间主电网减少对配电网22.5 kW 的有功注入，这部分由分布式电源来协同补偿；4～5 s之间主电网增加对配电网55 kW 的功率注入，分布式电源通过协同控制减少各自输出.传统的基于一致性算法的分布式电源有功经济调度有功输出和对应的一致性因子变化如图7～8所示.

图7 传统分布式电源输出有功协同控制Fig．7 Output active power collaborative control of traditional distributed generation

从图7～8可以看出：在使用传统的一致性算法协同控制时，对配电网的注入功率变化的情况下，对分布式电源的协同控制总能实现对参考值的实时跟踪，参与功率补偿的每台分布式电源在初始状态下其λP-i之间的差值较大，在1.71 s后才达到一致；在2 s和3 s时，主电网对配电网的功率注入发生变化后，λP-i在0.81 s后达到一致；在4 s时，主电网对配电网的功率注入发生变化后，λP-i在0.94 s后达到一致，且功率时刻达到供需平衡.从图8中一致性因子的变化可知：分布式电源在进行协同控制后，均衡了每个分布式电源之间的收益，但是因为节点之间通信线路较多，也造成了计算的复杂度提高.

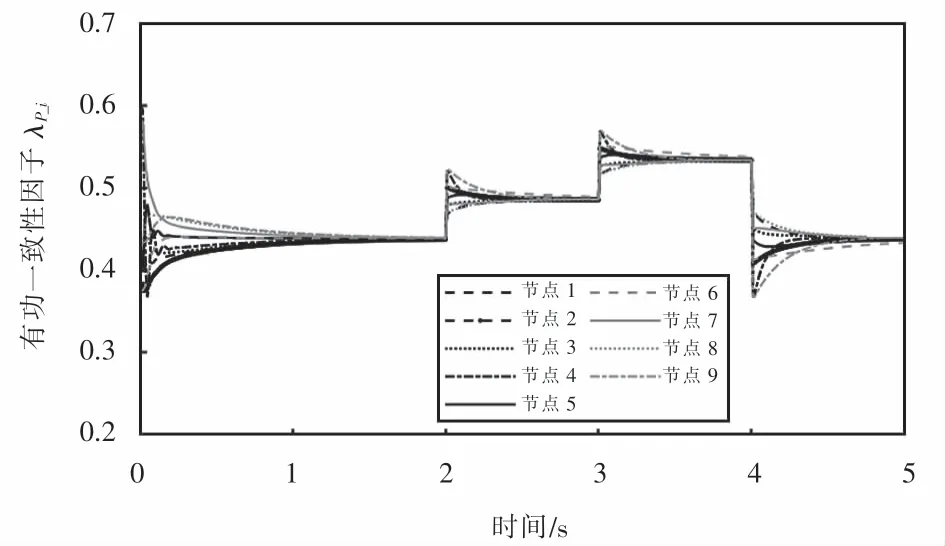
图8 传统分布式电源有功协同下一致性因子变化Fig．8 Variation of consistency factor under active power coordination of traditional distributed generation

针对无功的经济调度仿真分为3个阶段：0～2.5 s阶段，利用分布式电源对需要补偿的50 kvar无功进行经济调度补偿；因为电压的改变，将会造成对无功的需求改变，因此，在2.5 s时增加节点的电压分别为 -4，-2，1，-3，0，-2，-1，-4和 -1 V，在改变节点无功需求后，利用分布式电源对无功进行协同控制，进而对节点电压进行控制；在3.5 s时恢复初始电压状态，再次利用分布式电源对无功进行协同控制.对应的无功输出变化、电压变化和无功一致性因子的变化如图9～11所示.

从图9～11可以看出：在使用传统的一致性算法协同控制时，不管节点间的无功需求是稳态还是动态，分布式电源协同控制总是能动态的对系统的无功进行补偿，进而对节点电压进行控制，使其在要求的范围内，并均衡了每个分布式电源之间的收益，因为初始状态下每台分布式电源的λQ-i较大，因此，在1.97 s后λQ-i才达到一致；在2.5 s和3.5 s，主电网对配电网无功注入发生变化后，λQ-i在0.74 s后达到一致.因为使用了传统的通信机制，系统的收敛速度相对较慢，而且信息计算量大.

图9 传统分布式电源无功协同控制Fig．9 Reactive power cooperative control of traditional distributed generation

图10 传统分布式电源输出无功协同时电压变化Fig．10 Simultaneous voltage change of reactive power output of traditional distributed generation

图11 传统分布式电源输出无功协同时一致性因子变化Fig．11 Change of synchronous consistency factor of output reactive power of traditional distributed generation

为了解决一致性算法的收敛速度和计算量复杂的问题，采用本文提出的基于超节点协同一致性算法的分布式电源经济调度方案.其超节点的选取流程如图12所示，对图6所示的传统通信拓扑建立超节点，进行降维与重建，改进后相应的通信拓扑如图12所示.

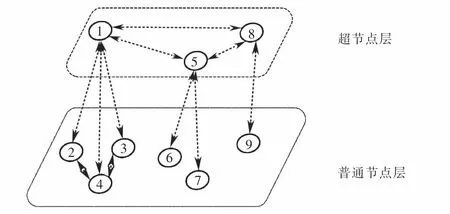
图12 建立超节点后的通信拓扑图Fig．12 Communication topology after establishing super nodes

由建立超节点通信拓扑前后的图进行对比后可知：在进行经济调度时，先将基本信息在普通节点层和超节点进行信息交互，在两层之间达到协同一致后，超节点层再次进行信息交互，最终需要达到超节点层之间、超节点与普通节点层、普通节点层之间协同一致.利用上述基于超节点的通信拓扑图再次对传统方式下的参数进行仿真，有功经济调度相关仿真结果如图13～14所示.

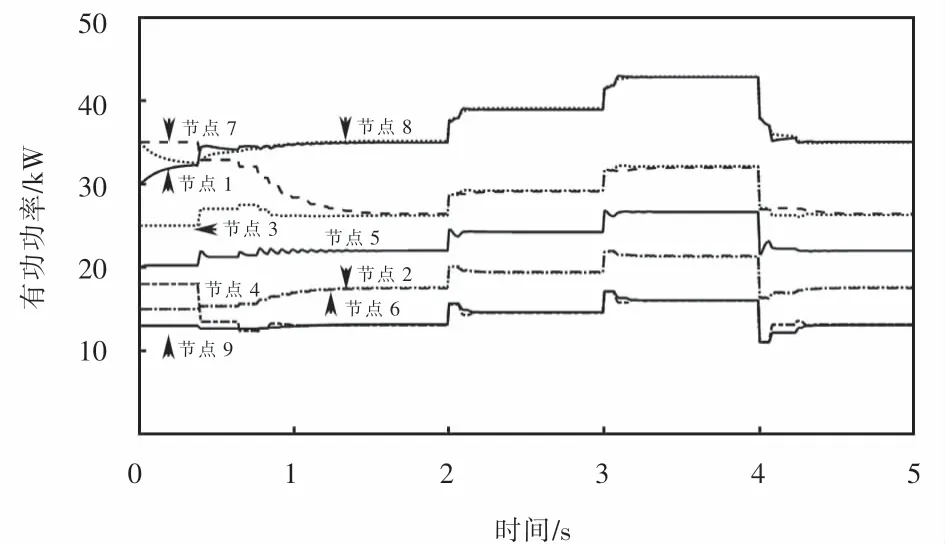
图13 超节点算法下分布式电源输出有功协同Fig．13 Distributed generation output active power cooperation under super nodes algorithm

图14 超节点算法下分布式电源有功协同一致性因子变化Fig．14 Variation of active power coordination consistency factor of distributed generation under super nodes algorithm

从图13～14可以看出：在使用基于超节点的一致性算法协同控制时，在配电网的注入功率变化的情况下，对分布式电源的协同控制同样能实现对参考值的实时跟踪，参与功率补偿的每台分布式电源在初始状态下的λP-i之间的差值较大情况下，在1.53 s之后就能达到一致；在2 s和3 s时，主电网对配电网的功率注入发生变化后，λP-i在0.32 s后达到一致；在4 s时，主电网对配电网的功率注入发生变化后，λP-i在0.49 s后达到协同一致，且功率时刻达到供需平衡.相比于传统通信机制下的协同一致性算法，该算法有效地提高了系统的收敛速度.

继续使用图12所示的具有超节点的通信拓扑进行无功功率的一致性协同调度，相关仿真结果如图15～17所示.

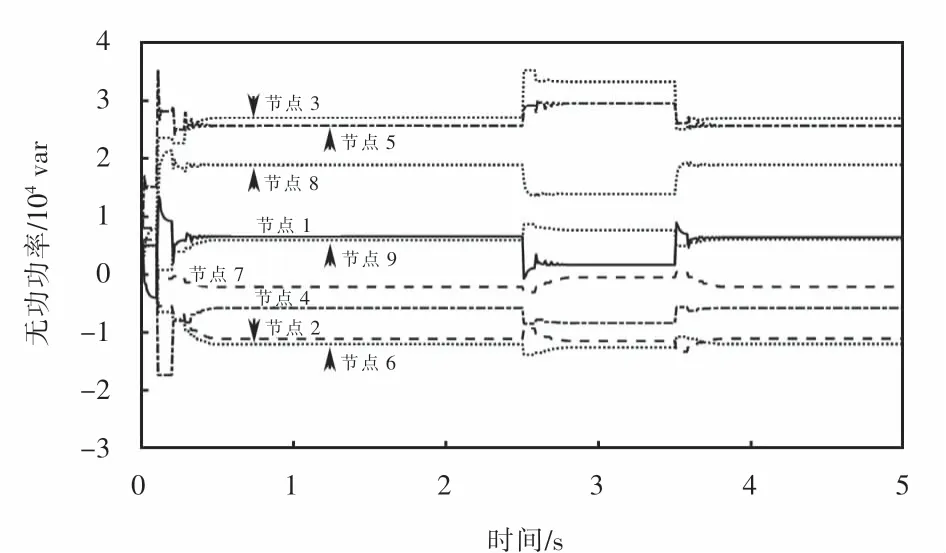
图15 超节点算法下分布式电源输出无功协同Fig．15 Distributed generation output reactive power coordination under super nodes algorithm

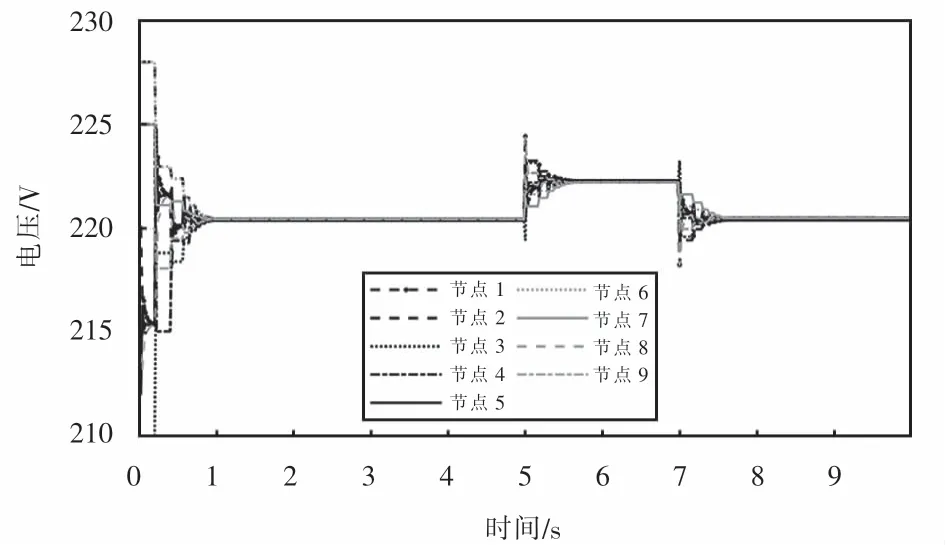
图16 超节点算法下分布式电源输出无功协同时电压变化Fig．16 Synchronous voltage change of reactive power output of distributed generation under super nodes algorithm

从图15～17可以看出：使用基于超节点的一致性算法协同控制时，不管节点间的无功需求是稳态还是动态的，分布式电源协同控制同样能动态地对系统的无功进行补偿，进而对节点电压进行控制，使其在要求的范围内；初始状态下当每台分布式电源的λQ-i较大情况下，在1.22 s后λQ-i就能达到一致；在2.5 s和3.5 s，主电网对配电网无功注入发生变化后，λQ-i在0.41 s后就能达到一致.相比于传统通信机制下的无功协同一致性算法，该算法同样可以有效提高系统的收敛速度.

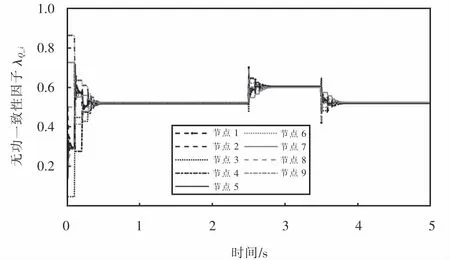
图17 超节点算法下分布式电源无功协同一致性因子变化Fig．17 Change of reactive power coordination consistency factor of distributed generation under super nodes algorithm

利用基于超节点的协同一致性算法对分布式电源进行调度时，某些曲线都出现了不同程度的锯齿波，这是因为在已知初始值状态下，超节点对应的一致性因子不同，因此，需要超节点之间先达到协同一致，然后，将超节点对应的值传递给普通节点.若此时超节点与普通节点间传递的值差距过大，就会引起超节点之间一致性因子差距过大，导致超节点之间的协同控制再次开始，也就造成超节点的值发生了跳动，而普通节点随着迭代时间的增加呈阶梯状.超节点之间值的抖动若直接接入变流器，则会造成其振动.为解决该问题，可以在变流器协同控制层的输出端口施加低通滤波器进行抑制.

经过两种方法的对比可以看出：基于超节点一致性算法的分布式经济调度过程中，系统也是能时刻达到供需平衡且达到对应的协同一致性；原有的通信拓扑被简化，以此来降低系统的计算量.对比前后仿真可以看出：基于超节点协同一致性算法在不改变分布式电源协同稳态值的情况下，可以在很短的时间内让各分布式电源的实际出力与最大出力的比值达到协同一致，收敛速度快，减少一致性算法的计算量和通信量，同时均衡了每个分布式电源之间的收益.

5 结论

本文在分布式电源的离散一阶一致性经济调度算法的基础上，考虑不同设备投资者间的收益分配，提出了基于超节点协同的分布式一致性经济调度算法.基于图信号降维和重建理论，首先，对分布式电源网络通信拓扑获得初始参数矩阵；然后，按照度矩阵参数和拉普拉斯参数选取超节点和局部集，进而得到粗化图；最后，根据一致性收敛系数算法，初始化相关参数.在14节点配电网系统中的实验仿真表明：该算法在不改变分布式电源协同稳态值的情况下，可以有效地提高分布式电源的协同收敛速度并减少计算量.