基于动态模式分解的三端多段式架空线-电缆混合输电线路故障定位新方法

张智伟，范新桥，张 利，李 慧，刘思嘉

（北京信息科技大学自动化学院，北京 100192）

随着城市化进程的推进输电线路的布局在不断地发生改变，为了城市的整洁美观及更好的利用空间和土地，城市内部的架空线不断减少，地下电缆逐渐增多，而城市周边一般仍采用架空线输电线路，逐渐形成了多段式架空线-电缆混合的输电线路格局，尤其以三端多段混合线路的情况居多。电缆相比于架空线路，由于深埋地下发生故障的概率较低，但随着使用时间的增长，电缆因绝缘老化发生故障的情况也时有发生。无论是架空线路还是电缆，一旦发生故障而不能快速修复，可能会造成巨大的经济损失，甚至是人员伤亡。对于深埋地下的电缆线路，因修复故障需要挖开电缆沟，其对故障点定位的准确性要求更高。

对于单一架空线或电缆的故障定位，国内、外已开展了较多研究[1-5]，且定位精度基本能够满足工程需要；对于三端或多端输电线路，目前的相关研究大都是基于单一架空线或电缆的均匀传输输电线路[6-8]。由于架空线-电缆混合线路的特性阻抗存在不一致性，会导致传统单一类型线路故障定位方法不再适用，这种混合线路的故障定位也是目前工程上未能很好解决的一个问题；对于多段式架空线-电缆混合输电线路，其线路结构比单一类型线路更加复杂，尤其多端多段式架空线-电缆混合输电线路具有更高的复杂性，因此该类结构的混合线路故障定位也更具挑战性。

对于架空线-电缆混合线路故障定位，文献[9]提出将混合线路等价成为一种均匀传输线路，并利用“波速归一化”的思想克服混合线路阻抗不连续的方法，从而解决了现场电缆波速难以确定的问题；文献[10-11]提出架空线与电缆连接点故障时，利用初始行波到达两端的时间差作为整定值，来判断故障发生区段的方法，然后分别利用双端行波故障测距算法和单端行波测距法求取故障距离。但这些文献均未进一步考虑含有多段架空线和电缆的故障点定位。文献[12-13]分别提出一种基于分段补偿原理和基于时间差值的混合输电线路行波故障定位方法，并考虑含有多段架空线和电缆的情况，但均未扩展到多端多段式混合输电线路的场景。多端多段式混合输电线路故障定位具有一定的复杂性，文献[14]提出一种基于时间轴整定的T型混合输电线路测距方法，但未考虑含有多段架空线和电缆的情况。

此外，基于行波原理的故障定位方法均需准确识别行波波头才能进行故障点的有效定位。基于小波分析的波头检测方法需要选择合适的基函数和分解尺度，自适应能力相对较差[15]；希尔伯特-黄变换HHT（Hilbert-Huang transform）[16]可以有效检测波头，但其存在过包络和欠包络问题。文献[6]、[8]分别提出了利用快速本征模态分解FIMD（fast intrinsic mode decomposition）和变分模态分解VMD（variational mode decomposition）识别故障初始行波波头，但这些方法都在一定程度上存在模态混叠问题。动态模式分解DMD（dynamic mode decomposition）算法[17]在处理非平稳信号方面具有很好的效果，该方法在提取主导特征值基础上实现信号低频分量的过滤来达到降低模态混叠现象的目的。此外，Teager 能量算子TEO（Teager energy operator）[18]能够有效反映分析信号能量的变化。结合DMD算法和TEO来检测故障行波波头到达时刻，具有一定的可行性。

三端多段式架空线-电缆混合线路相比常规混合线路故障定位更复杂，为得出较为普适性的故障定位方法，本文考虑了较为复杂的三端多段线路的混合情况，即各端支路均由多段架空线和多段电缆线路组成。

针对故障初始行波波头识别问题，本文提出基于DMD和TEO（DMD-TEO）的故障行波波头检测方法。首先，对于三端多段式混合输电线路故障定位，利用故障分支判定条件判断故障支路；然后，计算故障初始行波到达该支路端点和T 节点的时间差，并将其与故障行波从该支路各连接点传播到端点和T 节点的时间差进行比较；最后，确定故障所在的架空线路段或电缆线路段，并在故障线路段上利用双端行波原理计算出故障距离。

1 基于DMD-TEO 的故障行波波头检测方法

1.1 动态模式分解

DMD 算法是一种基于Koopman 算子理论发展起来的模态分析算法，被广泛应用于非线性系统数据处理，对处理非平稳信号具有很好的效果[19-21]。给目标信号进行DMD分解，就是通过数学变换，有效过滤掉故障行波中的低频分量，得到主导特征值和主要模态，从而减少模态混叠现象对行波检测精度的影响。

通过行波采样装置可以获得包含故障信息的行波数据X=[x1,x2,x3,…,xN]，其中，xi为第i时刻的采样值。离散的采样数据可以通过线性映射表示为

式中，A为离散系统的状态矩阵。

将上述采样数据X构建成2 个新的矩阵X1=[x1,x2,x3,...,xN-1] 和X2=[x2,x3,x4,...,xN]，并满足如下关系：

对矩阵X1进行奇异值分解SVD（singular value decomposition），即

式中：U、V为酋矩阵；Σ为奇异值对角矩阵；A′为状态矩阵A的近似矩阵。

矩阵A′的计算过程可视作Frobenius范数的最小化问题，即

可将A近似为

从而，实现对原高维状态矩阵的有效降维，且矩阵A′包含的行波故障特征信息与原状态矩阵A一致。对矩阵A′进行特征值分解，从而获得包含故障特征信息的模态量。

对矩阵A′进行特征分解，即

式中，μi、wi分别为A′的特征值和特征向量。

在求解出所有的特征值和对应的特征向量后，构建矩阵W和对角矩阵D，且wi为W的列向量，μi为D的对角元，其关系可表示为

定义φ的每一列为一个DMD 模态，则DMD 模态可表示为

至此，完成对行波信号的DMD分解，从而得到含有行波故障信息的主要模态。

1.2 基于DMD-TEO 的行波波头检测方法

TEO 是一种能反映被分析信号能量变化的非线性算子，其通过对信号进行差分运算来获得信号的瞬时能量。对TEO进行离散化，即

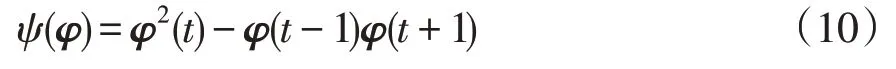
式中：ψ为能量算子；t为时间。

当输电线路发生故障后，行波浪涌的到达表现为能量的突变，在原理上能够采用TEO算子检测行波能量突变。因此，结合DMD 算法及TEO 算子来检测故障行波波头到达时刻。首先，对故障电流行波进行凯伦贝尔解耦变换[22]；然后，对所得故障行波线模分量进行DMD分解；最后，利用TEO算子即可计算出模态1的瞬时能量。

2 三端三段式混合线路的故障定位方法

2.1 故障分支判定条件

图1 为结构较为简单的三端三段式架空线-电缆混合输电线路，其中，F为故障点，K1、K2为架空线与电缆连接点；K1K2段为电缆线，长度为L12；S1K1段、K2T 段、S2T 段、S3T 段均为架空线，长度分别为L11、L13、L2、L3。

图1 三端三段式混合线路Fig.1 Three-terminal three-segment hybrid line

假定故障行波在架空线和电缆中的波速分别为v0、vc，则故障行波穿过S1K1、K1K2、K2T、S2T 和S3T 段线路所用时间t11、t12、t13、t2和t3可表示为

在此基础上对图1 所示的三端三段式混合线路进行简化，简化后的三端输电线路如图2所示。

图2 三端简化线路Fig.2 Simplified three-terminal line

简化前、后S1-T 线路段的长度对应关系可表示为

设故障行波穿过S1T 段所用总时间为t1，则有

故障行波从T 节点传播到三端测点的时间差可预先计算出来，分别为

式中：ΔtS1TS2为故障初始行波从T 节点传播到S1端和S2端的时间差；ΔtS1TS3为故障初始行波从T 节点传播到S1端和S3端的时间差；ΔtS2TS3为故障初始行波从T节点传播到S2端和S3端的时间差。

故障发生后，故障初始行波到达三端测点的时刻分别为tS1、tS2和tS3，两两作差可得

式中：ΔtS1S2为故障初始行波到达S1端和S2端的时间差；ΔtS1S3为故障初始行波到达S1端和S3端的时间差；ΔtS2S3为故障初始行波到达S2端和S3端的时间差。

根据故障初始行波到达各端测点的时间差和行波从T 节点传播到各端测点时间差之间的大小关系，可对三端混合线路故障分支判定条件进行如下梳理。

（1）在图2中当故障点发生在S1-T 支路时，对故障初始行波到达S1、S2端的时刻tS1和tS2作差可得ΔtS1S2为

式中，tFT为故障初始行波从故障点F传播到T节点所用时长。

由于ΔtS1TS2=t1-t2，因此可得ΔtS1S2＜ΔtS1TS2。同理，可得特征关系为

（2）当故障点发生在S2-T、S3-T 支路时，可分析出各时间差的特征关系为

（3）当故障点发生在T 节点时，各时间差具有的特征关系为

因此，当故障发生在三端混合线路的任何一条支路上时，根据式（18）～（21）基于时间差的故障分支判定条件即可判定出故障所在支路。

2.2 故障分支内故障线路段判断

判断出故障点在某一分支线路后，由于分支线路可能存在多段架空线和电缆的混合线路，因此需进一步判断故障点是在该分支混合线路的哪段电缆或架空线。

假定图1 中S1-T 支路上F 点的故障发生时刻为tF，故障初始行波以v0的速度沿着架空线路向两端传播，分别在tS1和tT时刻到达S1测点和T 节点。其中，tT时刻可由故障初始行波到达S2端测点的时刻和到达S3端测点的时刻分别计算，即

考虑只用其中一端测点检测到的行波到达时刻计算可能会造成较大误差，故使用两者均值作为T节点检测到故障初始行波的时刻，其计算方法为

式中，tT为故障初始行波到达T节点的时刻。

由于实际线路拓扑是已知的，故障行波从K1、K2点分别传播到S1测点和T 节点的时间差ΔtS1K1T和ΔtS1K2T可表示为，

因此，故障初始行波传播到S1测点和T节点的时间差可表示为

将ΔtS1T与ΔtS1K1T和ΔtS1K2T进行比较，来确定故障发生区段，具体方法如下。

（1）当故障点发生在S1K1区段时，故障行波从故障点传播到S1测点的时间小于行波从K1点传播到S1测点的时间，此时ΔtS1T＜ΔtS1K1T。

（2）当故障点发生在K1K2区段时，故障行波从故障点传播到S1测点的时间大于行波从K1点传播到S1测点的时间，同时小于从K2点传播到S1测点所用的时间，此时ΔtS1K1T＜ΔtS1T＜ΔtS1K2T。

（3）当故障点发生在K2T 区段时，故障行波从故障点传播到S1测点的时间大于行波从K2点传播到S1测点的时间，此时ΔtS1T＞ΔtS1K2T。

因此，根据故障初始行波传播到S1测点、T 节点的时间差ΔtS1T和故障初始行波由K1、K2点分别传播到S1测点、T 节点的时间差ΔtS1K1T及ΔtS1K2T三者之间的大小关系，即可判断出故障点所在故障分支内的电缆段或架空线路段。

2.3 故障点定位原理

在判断出图1 所示的故障线路段K2-T 后，进一步采用双端行波法计算故障距离。根据各段架空线和电缆段线路长度，计算故障行波在各线路段的传播时长；利用各端检测到的故障初始行波到达时刻计算故障行波到达故障段线路K2-T 两端的时间，从而进行故障距离计算。故障初始行波到达电缆和架空线的接头K2点的时刻tK2可表示为

利用双端行波法可计算故障点F 到电缆和架空线接头K2点的距离LK2F为

进而计算故障点F到S1端的距离LS1F为

3 三端多段式混合线路的故障定位方法

图3 为含有n（n＞1）段架空线和电缆的多段式混合输电线路示意，Kj(j=1,2,…,n-1)为各段架空线和电缆的接头。根据第2 节的三端三段式混合输电线路故障定位原理，可进一步分析得出三端多段式混合线路的故障定位，其具体步骤如下。

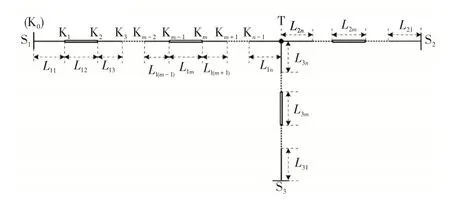
图3 三端多段式混合线路Fig.3 Three-terminal multi-segment hybrid line

步骤1根据三端多段式混合线路的拓扑，确定各分支线路内的各段架空线、电缆的长度及参数。假定各支路内架空线和电缆的总段数为n，第i条分支线路第j段架空线或电缆线路长度为Lij，第i条分支线路第j段架空线或电缆线路故障行波传播速度为vij，i=1,2,3，j=1,2,…,n。例如，L12和v12分别表示S1端所在支路K1-K2段线路长度和故障行波在该线路段的传播速度，此时i=1，j=2。

步骤2计算故障行波在第i条分支线路内第j段线路中的传播时长tij为

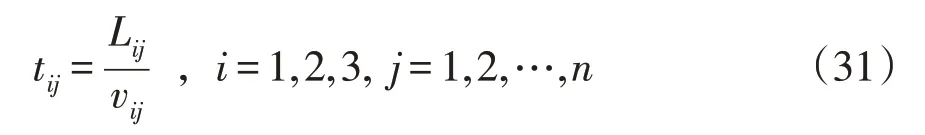
同理，可将图3 的三端多段式混合线路简化为图2的形式。其中，S1-T、S2-T、S3-T 线路段的长度L1、L2、L3及故障行波穿过S1T、S2T、S3T 段所用总时间t1、t2、t3可分别表示为

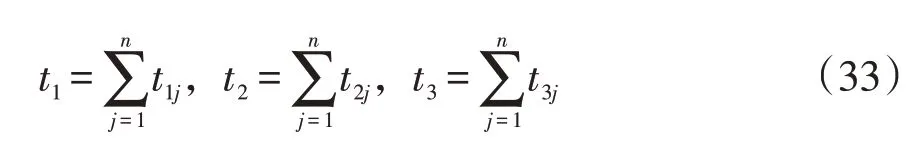
式中，j=1,2,…,n，n为各支路内架空线和电缆的总段数。

步骤3按照式（15）和式（16）计算出ΔtS1S2与ΔtS1TS2、ΔtS1S3与ΔtS1TS3、ΔtS2S3与ΔtS2TS3，并根据三端三段式混合线路故障分支判断方法，通过比较该时间差的大小关系可判断出故障支路。

步骤4如果比较结果符合式（21）的特征，则可以判定故障点发生在T节点位置，其到Si端的距离LSiF可表示为

式中，i=1,2,3，j=1,2,…,n。

步骤5如果比较结果为式（18）～（20）的结果，则可以判定故障点发生在S1～S3端所在支路。

步骤6由步骤（5）判定出故障发生支路，计算故障初始行波由该支路各连接点Km传播至该支路Si端和T节点的时间差ΔtSiKmT为

式中 ：i=1,2,3 ；m为连接点个数，m=0,1,2,…,n-1；ti0=0。

计算故障初始行波到达Si端点和T 节点的时间差ΔtSiT=tSi-tT，并与ΔtSiKmT分别进行比较，来确定故障发生区段，并进行故障距离计算，具体比较方法如下。

（1）如果ΔtSiT=ΔtSiKmT（m=0，1，2，…，n-1），则可判定架空线和电缆的连接点或端点Km为故障点。其到端点Si(K0)距离可表示为

（2）如果ΔtSiT满足的条件为

则故障点发生在第m段线路上。故障点到Si端点的距离可表示为

4 三端多段式混合线路故障定位仿真验证

4.1 仿真模型

图4为采用电磁暂态程序PSCAD/EMTDC 搭建的三端多段式混合输电线路模型。其中，输电线路采用贝杰龙模型，电缆为三芯结构；架空线及电缆线路参数见表1，系统阻抗见表2。

图4 仿真系统结构简图Fig.4 Simplified structural diagram of simulation system

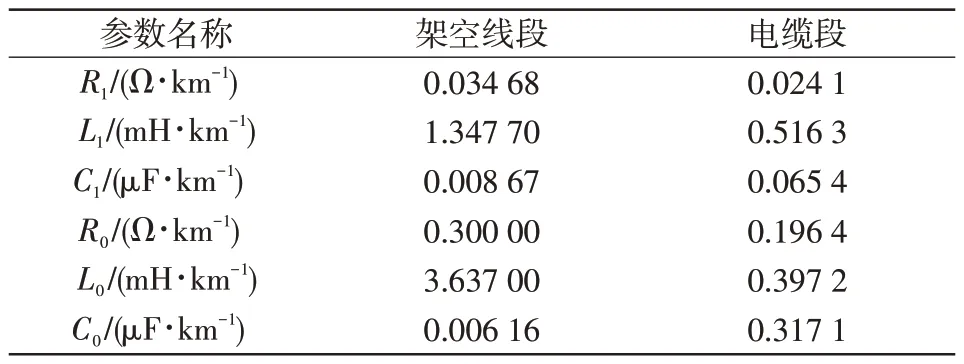
表1 输电线路参数Tab.1 Parameters of transmission line

表2 系统阻抗Tab.2 System impedances Ω

4.2 仿真计算及分析

对不同短路故障类型进行仿真，仿真步长设置为1 μs，过渡电阻为150 Ω、100 Ω、50 Ω；0.3 s 时刻发生故障，持续时间为0.1 s。

根据线路拓扑结构和线路长度预先计算行波在各段架空线和电缆的传播时间如表3所示。

表3 各段线路传播时长Tab.3 Propagation duration of each section of line μs

将图4 简化为三端线路后，根据式（33）计算行波在S1T、S2T、S3T 分支上的总传播时间t1、t2、t3分别为481.972 μs、287.132 μs、240.986 μs。

根据式（15）可计算故障行波从T 节点传播到S1、S2和S3端测点的时间差为ΔtS1TS2=194.84 μs、ΔtS1TS3=240.986 μs、ΔtS2TS3=46.146 μs。

考虑实际系统的单相接地故障发生概率最高，限于篇幅，本文只对接地电阻为50 Ω时的A相接地短路故障的仿真计算过程进行详细说明。

1）分支线路故障

在图4中，S1测点所在支路S1-T 上距S1端30 km处发生A 相接地短路故障（对应位置①）后，S1、S2和S3端的瞬时电流波形分别如图5（a）～（c）所示。

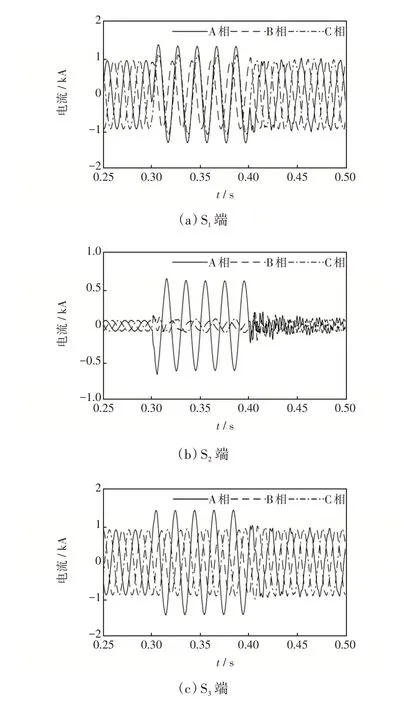
图5 三端瞬时电流波形Fig.5 Three-terminal instantaneous current waveform

由0.299 901s开始截取1 000个采样点，用采样点代表采样时刻，对各测点解耦后的α模电流分量进行DMD分解。其中，S1测点的DMD分解结果如图6 所示；图7～9 为各测点模态1（DMD-1）的Teager 能量曲线。

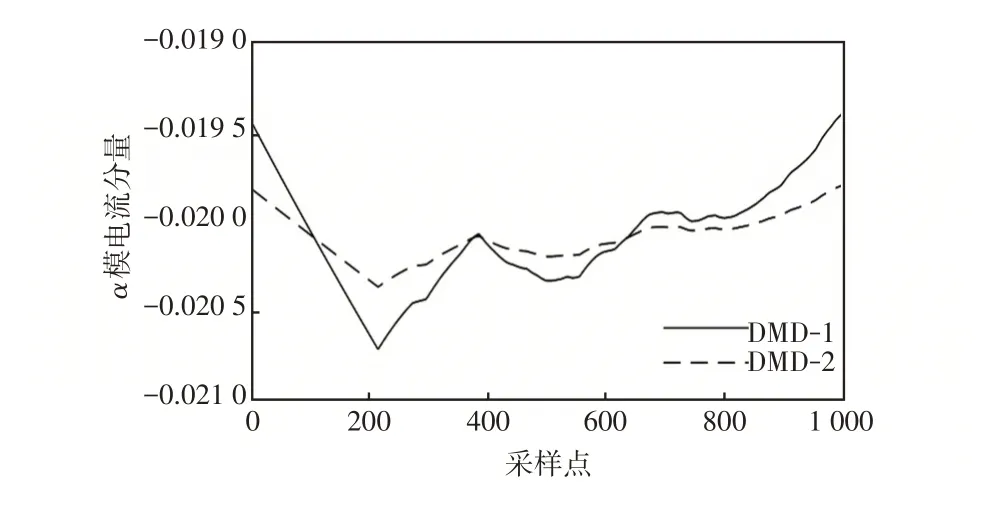
图6 S1 测点的α 模电流DMD 分解结果Fig.6 DMD results of Mode-α current at S1

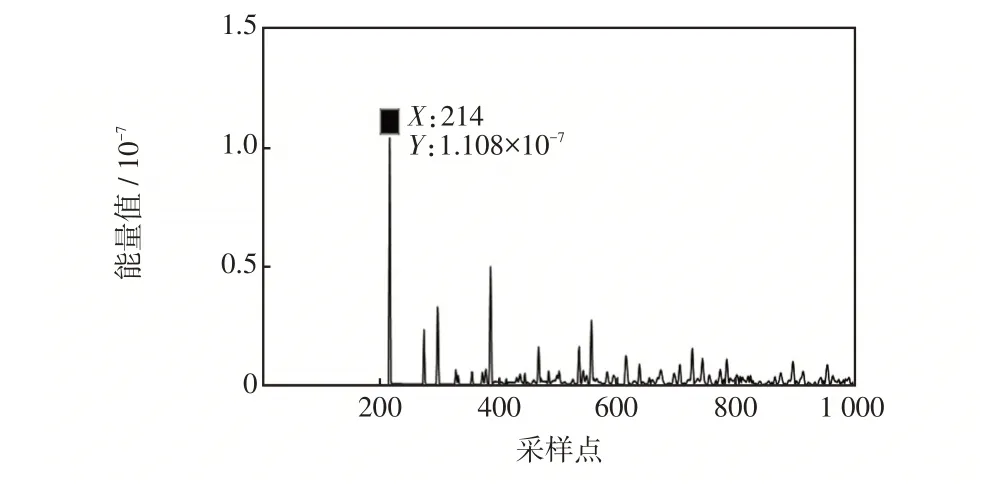
图7 S1 测点所得DMD-1 的Teager 能量曲线Fig.7 Teager energy curve of Mode-1 at S1

图8 S2 测点所得DMD-1 的Teager 能量曲线Fig.8 Teager energy curve of Mode-1 at S2

图9 S3 测点所得DMD-1 的Teager 能量曲线Fig.9 Teager energy curve of Mode-1 at S3

故障初始行波到达各测点时刻如表4 所示，各端测点故障行波到达时刻由采样点序号乘以采样周期来计算，即tS1=0.299 9+214×10-6=0.300 114 s。

表4 仿真情况1 的各测点初始行波到达时刻Tab.4 Arrival time of initial traveling wave at each measuring point in simulation Case 1 s

由式（16）可得出故障初始行波到达三端测点的时间差分别为ΔtS1S2=-540 μs、ΔtS1S3=-494 μs、ΔtS2S3=46 μs。

利用故障分支判定条件判断故障发生分支时，由于存在一定误差，需对故障分支判定条件进行修正。假设误差阈值为λ，当“|ΔtS2S3-ΔtS2TS3|＜λ”时，修正为“ΔtS2S3=ΔtS2TS3”。一般误差阈值λ的值可取为1×10-5左右。

由故障分支判定方法可知，修正后故障初始行波到达各端测点的时间差和行波从T 节点到达各端测点的时间差之间的特征满足式（18），因此可以判定故障发生在S1测点所在支路。

由式（35）可计算故障初始行波由S1-T 支路的各个连接点K1、K2、K3和K4分别传播至S1端和T节点的时间差为ΔtS1K1T=-311.058 μs、ΔtS1K2T=-171.596 μs、ΔtS1K3T=67.684 μs、ΔtS1K4T=276.876 μs。

故障初始行波到达S1端点和T 节点的时间差ΔtS1T可根据式（27）计算为ΔtS1T=-252.941 μs。

由第2.2节故障区段判定方法可知ΔtS1T满足的条件为ΔtS1K1T＜ΔtS1T＜ΔtS1K2T，因此，可判定故障发生在K1K2区段。由式（38）可计算出故障点到S1端的距离LS1F=L11+LK1F=25+5.000 7=30.000 7 km，定位误差为0.7 m。。

2）T节点故障

当图4 网络的T 节点处发生A 相接地故障（对应位置为②）时，表5 给出了三端测点故障初始行波的到达时刻。

表5 T 节点故障时各测点初始行波到达时刻Tab.5 Arrival time of initial traveling wave at each measuring point under T-node fault s

由式（16）可得故障初始行波到达3 端测点的时间差分别为ΔtS1S2=194 μs、ΔtS1S3=241 μs、ΔtS2S3=47 μs。

由故障分支判定方法可知，修正后故障初始行波到达各端测点的时间差和行波由T 节点到达各端测点的时间差之间的特征满足式（21），因此可以判定故障点发生在T节点。

部分不同故障工况下的故障定位结果如表6所示。

表6 故障定位结果Tab.6 Fault location results

由表6 的定位结果表明，本文方法在不同故障工况下均能准确定位出故障支路和故障点，定位误差基本保持在100 m以内，能够满足实际工程需求。

4.3 不同波头检测方法的定位结果比较

为比较本文波头检测方法下的故障定位效果，在S1-T 支路不同位置处模拟了多种不同过渡电阻、不同类型的故障工况。利用本文所提基于DMD-TEO的故障定位方法和基于小波变换的波头检测方法进行故障定位效果对比，两种方法的部分定位结果如表7所示。

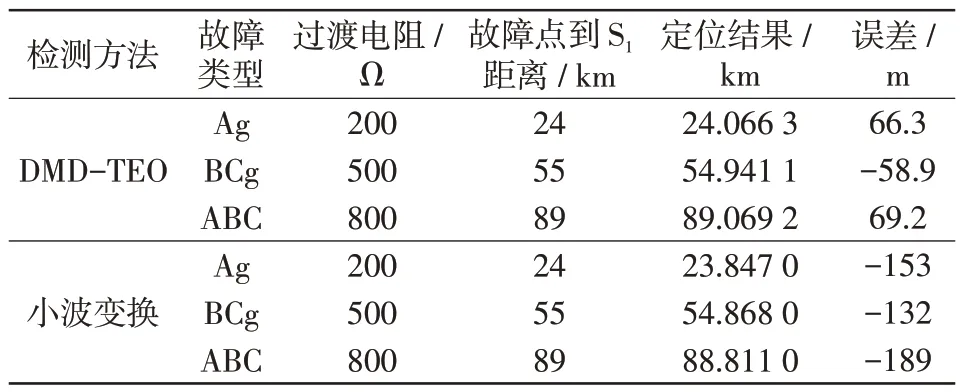
表7 不同方法定位结果Tab.7 Location results obtained using different methods

由定位结果可以看出，本文方法的定位误差绝对值最大为69.2 m，在相同故障工况下所提DMDTEO方法的故障定位精度均高于小波变换方法，且不受故障类型和过渡电阻影响。因此，当故障发生在架空-电缆分界点附近时，本文方法也能得到较为满意的定位效果。

5 结论

（1）鉴于DMD 可改善模态混叠和TEO 能有效反映能量的瞬时变化，结合DMD算法和TEO算子，本文提出一种DMD-TEO 的故障行波波头检测方法，实现故障初始行波到达时刻的准确检测。

（2）提出一种基于故障初始行波到达各端测点及T节点时间差的故障线路段判断方法，该方法在判定出故障分支线路后，进一步计算故障初始行波到达该支路端点和T节点的时间差，并与故障行波从该支路各连接点传播到端点和T 节点的时间差进行比较，确定故障所在的架空线路段或电缆线路段，利用双端行波法实现故障距离的准确计算。

（3）在PSCAD 中搭建三端多段式架空线-电缆混合线路模型，利用本文所提故障定位方法对不同支路的架空线、电缆段在不同位置发生不同类型、不同过渡电阻的多种故障工况下进行定位验证，结果表明，利用本文方法能够准确判定出故障支路和故障所在的架空线或电缆线路段，并准确定位故障点，从而验证了本文所提三端多段式混合线路故障方法的有效性。