考虑时序最优潮流的分布式电源优化配置方法

马世乾，张 杰，商敬安，王天昊，梁 刚，张 鑫

（1.国网天津市电力公司电力科学研究院，天津 300384；2.国网天津市电力公司，天津 300010）

分布式风机、光伏是开发新能源发电的重要形式，传统的无源配电网将逐渐发展成为主动配电网[1]。然而，由于风电、光伏等可再生能源机组的出力存在很强的波动性，伴随着新能源并网容量的增加，配电网运行中面临着节点电压越限、峰谷功率平衡困难等重大运行挑战[2-3]，将不可避免地出现弃风、弃光现象。因此，如何在保证分布式电源消纳效果的前提下，实现分布式电源在主动配电网中的最佳配置，成为电力行业关注的热点问题。

已有大量研究对分布式电源优化配置问题进行建模，所建模型的目标函数各有侧重，通过单目标优化或多目标优化以使分布式发电的效益最大化。在单目标优化模型中，通常以配电网实际功率损耗[4]和电压偏差[5]最小为基本目标；部分学者还以无功功率最小化[6]或分布式电源容量最大化[7]为目标对分布式电源开展优化配置。分布式电源优化配置模型中还包括多目标优化模型，考虑配电网运行的时序特性，文献[8]以多时段功率损耗最小、电压偏离最小和电压无功优化中需求响应利用率最大化为多目标函数，建立分布式新能源配电网电压无功协同控制的多时段多目标动态优化模型。已有研究大多侧重分布式电源渗透率对系统安全稳定的影响或降低系统功率损耗等方面，未能分析系统供电经济性与渗透率之间的关系，也未能得出使系统供电成本最低的分布式电源渗透率。

分布式的风机和光伏设备一般接入中低压配电网，电压和线路容量是限制穿透功率极限的关键要素。文献[9]计及了电压约束，发现电压越限是制约分布式光伏大量接入中低压配电系统的关键要素；文献[10]提出一种基于电压敏感度的直接计算分布式风机传统功率极限的计算方法。计及线路潮流约束将影响风、光电能的消纳效果[11]，但分布式电源多点接入配电网，将引起复杂的潮流分布，当系统的安全约束越限时，需要切除机组尖端出力，如何针对多个分布式电源制定最优的消纳方案是复杂的最优潮流问题。

已有文献利用启发式算法制定风机、光伏的最优消纳方案，文献[12]利用粒子群优化算法，以使配电网中的分布式发电机组在实际功率中的总损耗最小化为目标函数制定风机、光伏的消纳方案。以功率损耗最小化、运行成本最小化和提高网络电压稳定性为目标，文献[13]提出小偷与警察博弈算法求解分布式电源的最优消纳方案；文献[14]提出基于差分进化算法来实现分布式电源的最优消纳；文献[15]以2 条母线之间的电压差最小为目标函数，利用粒子群优化算法求解配电网分布式电源消纳方案。然而，单纯依靠传统的智能算法往往会使求解过程易陷入局部最优解，且需要反复进行潮流计算，从而使模型求解时间过长。

此外，在分布式电源优化配置研究中还需计及分布式电源出力的不确定性。目前，处理可再生能源功率预测不确定性的主要方法有：①增加旋转备用[16]，这种方法简单、可靠，但由于目前风电功率的预测误差仍然较大，预留旋转备用的容量大小难以确定；②鲁棒优化方法[17]，鲁棒优化的思想是将风电的不确定性转化为不确定解集的形式，考虑最恶劣的场景，往往使调度结果比较保守，经济性较差；③基于机会约束规划的随机建模方法[18]，这种方法对于规模较大的电力系统难以推导出解析的机会约束模型，而且设置何种置信水平也难以客观确定；④基于场景集的优化方法[19]，该方法会使需要开展优化的场景集较多，而利用场景缩减的方法需要牺牲一定的计算精度。因此，通过时序仿真更能反映配电网在计及节点电压、线路潮流等约束条件下，对分布式电源的真实消纳能力。

从系统运行的角度，风、光机组发电不消耗化石能源，风、光功率的注入可以减少同时段其他电源的出力，从而降低系统的供电成本，因此“弃风、弃光”往往被认为是一件不好的事情；然而，从系统规划的角度，风、光机组的出力具有显著的季节性、间歇性特征，新能源小发期间供电占比较低和大发期间消纳困难的情况频繁交替出现，如果允许新能源机组在大发期间适当弃置部分尖峰功率，可以提高小发期间的供电占比，从而提升系统全年的新能源电量渗透率和供电经济性。

综上所述，为了适应“双碳”目标的发展要求，未来的主动配电网应以适当弃置风、光电量为代价来提高新能源的渗透率，而已有的研究在弃风、弃光方案的快速制定和可再生能源的经济消纳方面存在不足。本文提出一种基于主动配电网时序最优潮流分析的分布式电源优化配置方法，其特点是提出可再生能源经济消纳的观点，采用运行-规划一体化的研究思路，根据电力系统的供电成本指标动态评估分布式电源的最佳配置方案。

1 配电网分布式电源优化配置模型

1.1 弃风、弃光比例与分布式电源的优化配置

对含有N个节点的配电系统，当并网分布式电源容量较小时，能够实现风、光电量的100%消纳，清洁的风、光电能减少了该配电系统从上级电源的购电量，降低系统的单位电能供电成本；随着新能源机组并网容量的逐步增加，由于电网安全运行约束的存在，风、光机组的尖峰出力将不能被消纳，开始出现弃风、弃光现象，使系统的单位电能供电成本下降速度变缓。将第i个节点的新能源机组充分利用当地风、光资源时，该机组每年可发出的最大电量记为，在配电系统运行约束下被消纳的电量记为，则该节点的弃风、弃光比例指标Rrej,i可表示为

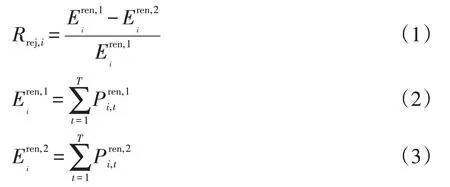
式中，N为配电系统的节点总数。

继续增加并网风、光机组，会使弃风、弃光电量进一步增多，弃风、弃光比例升高，最终使系统供电经济性出现拐点，此时系统的单位电能供电成本达到最低，弃风、弃光措施与系统灵活资源之间实现最优配合；如果继续向该系统中增加并网风、光机组，会导致弃风、弃光比例进一步升高，由于大量风、光设备闲置而使系统单位电能供电成本上升。由此可见，在供电经济性方面，该配电系统能够接纳的风、光机组存在某个最优容量，此时系统的单位电能供电成本最低，实现分布式电源的优化配置。

1.2 分布式电源优化配置模型

1.2.1 单位电能供电成本

配电网中第i个节点的分布式电源装机容量记为Pi，系统内负荷的电能需求首先由分布式电源提供，缺额部分由上级电网补充，优化配置模型的目标函数是年平均单位电能供电成本最小。供电成本主要包括系统的投资成本C1和从上级电网购电的成本C2，决策变量是分布式电源装机容量向量P=[P1,P2,…,PN]。

1）系统的投资成本

C1包括设备投资成本和运行维护成本，本文采用等年值方法计及设备投资成本，等年值系数c可表示为

式中：r为银行贴现率；y为设备的运行年限。

运行维护成本一般按照设备投资成本的固定比例计及，则C1可表示为

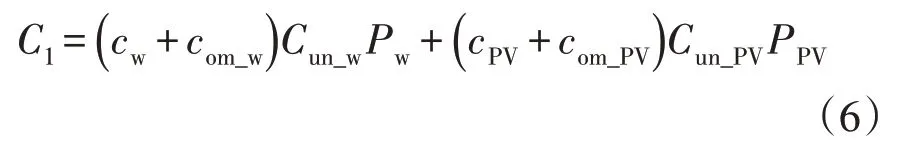
式中：cW、cPV分别为风机和光伏的等年值系数，可通过式（5）得到；com_W、com_PV分别为风机和光伏的运维比例；Cun_W、Cun_PV分别为风机和光伏的单位容量投资成本；PW、PPV分别为该配电网中风机和光伏设备的总装机容量，可根据装机容量向量P得到。

2）购电成本

配电系统通过配电变压器与上级电网相连，购电成本C2可表示为

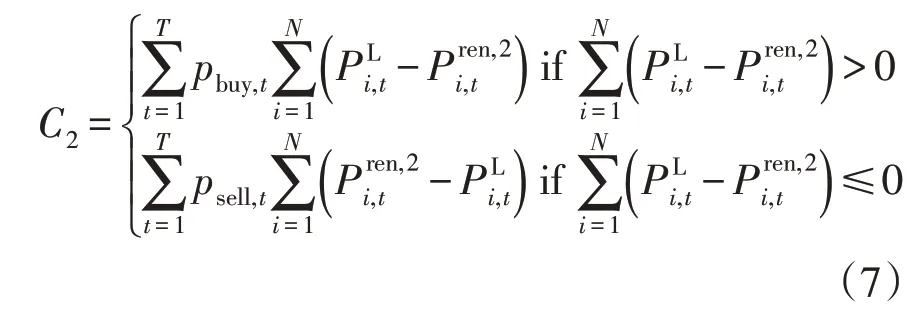
式中：pbuy,t为该配电网从上级电网买电的实时电价；psell,t为该配电网向上级电网卖电的实时电价；为第i个节点负荷的有功功率；为第i个节点分布式电源t时刻在弃风、弃光操作之后的实际注入有功功率。

系统的单位电能供电成本CkWh可表示为

1.2.2 最大最小优化配置模型

1）目标函数

外层模型是配电网中分布式电源优化配置模型，对配电系统开展优化配置的目的是确定高比例分布式电源的接入容量和接入位置，根据式（4）～（6）可得模型的目标函数为

式中，CkWh为系统的单位电能供电成本。

2）约束条件

节点功率平衡约束为

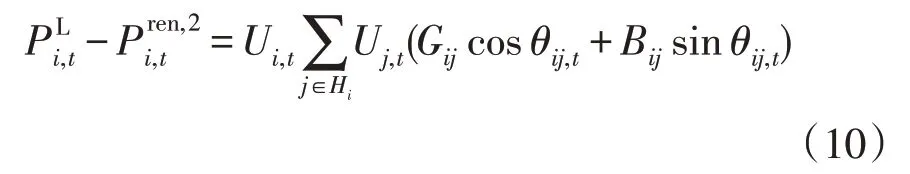
式中：Ui,t、Uj,t分别为节点i和节点j在t时刻的电压幅值；θij,t为节点i和节点j在t时刻的相位差；Gij、Bij分别为节点i与节点j之间的电导和电纳；Hi为与节点i相连的节点集合。

配电网中节点电压幅值存在上、下限约束，为保证系统的安全稳定运行，支路潮流存在的上限约束为

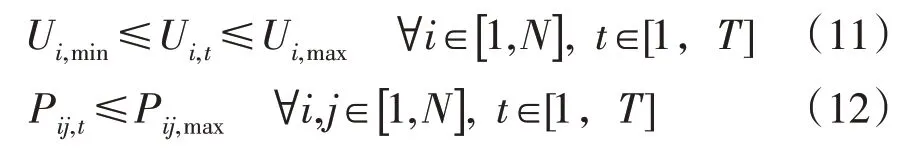
式中：Ui,min、Ui,max分别为节点电压幅值的下限和上限；Pij,t、Pij,max分别为节点i与节点j之间t时刻的有功功率和传输容量上限。

此外，配置分布式电源时还需考虑节点并网线路容量约束、上级电网调度要求约束、可再生能源机组出力约束、分布式电源容量配额约束等。各约束分别表示为

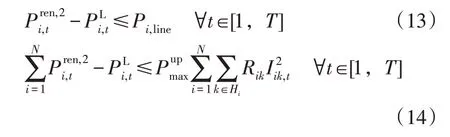
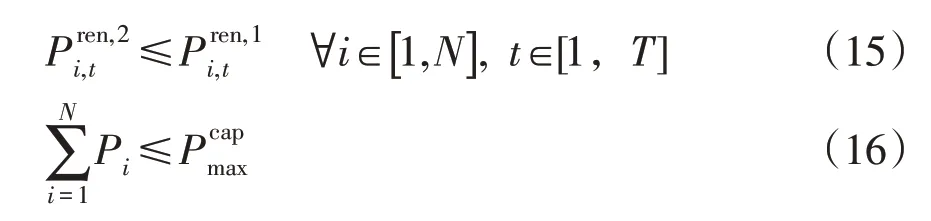
式中：Pi,line为节点i上行功率上限；为配电网向上级电网倒送功率的上限；Rik为节点i与节点k之间线路的阻抗；Iik,t为流经节点i与节点k之间线路的电流；为第i个节点分布式电源t时刻的最大出力，由气象预测数据和风、光机组的出力特性得到；为配电网允许接入的分布式电源配额上限。不难发现，本文所建立最大、最小优化配置模型的核心工作包括两部分：一是求解内层的最大化模型，即对时间断面上分布式电源的时序出力进行优化，也就是有源配电网的最优潮流问题；二是求解外层的最小化模型，即通过系统供电成本指标选择最优的P，也就是分布式电源的经济消纳问题。

2 基于配网安全域的分布式电源优化配置模型求解策略

为了使第1 节的最大最小模型可解，需要将模型进行拆解。本文把配电网静态安全域方法引入该模型的求解过程，对连续变量和向量P提出高效、快捷的求解方法。

2.1 优化配置模型的快速求解方法

对于内层最优潮流问题，由于电力系统的潮流方程是分布式电源时序出力的非线性方程，节点电压和支路潮流是分布式电源时序出力的非线性函数，因此式（10）～（12）约束的存在使所建立的最大、最小优化配置模型成为非线性模型；对于外层经济消纳问题，向量P的维度高并连续变化，传统的广度优先、插值遍历等搜索方式将导致求解效率低下，需要利用某种启发信息来制定较好的初始解并指出搜索方法。

2.2 有源配电网最优潮流的快速求解

对于给定分布式电源配置方案P的有源配电网，尽可能多地消纳可再生能源电量，能够减少配电网从上级电网购电的成本，进而降低系统的平均供电成本。根据配网安全域方法[20]，非线性约束条件式（11）和式（12）可由超平面线性表达式等效表达。主动配电网的最优潮流模型可表示为

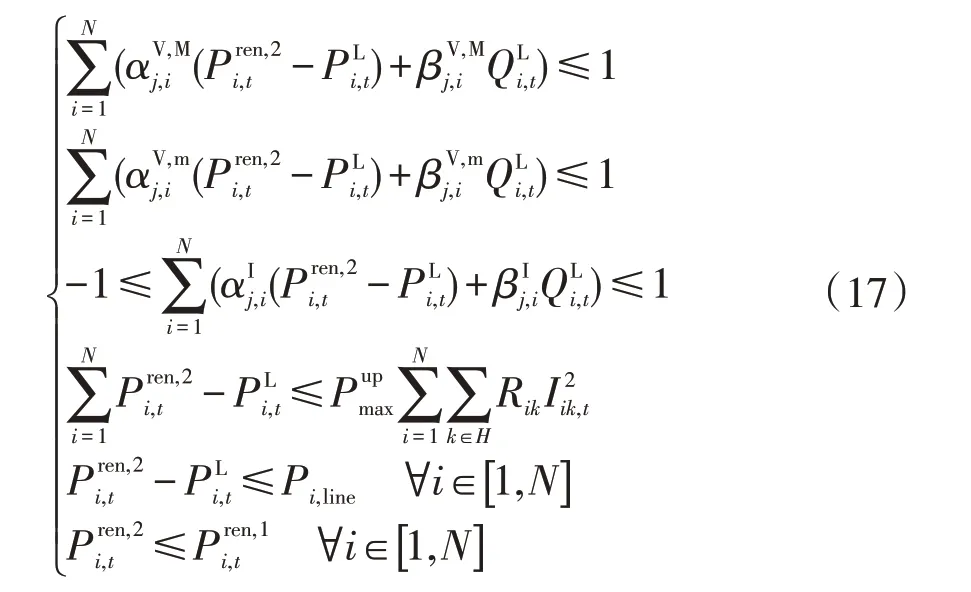
该线性配置模型可通过CPLEX 等商业软件进行快速求解，从而确定各个分布式电源的实际出力。

2.3 分布式电源配置方案的快速制定方法

（1）在不允许弃风、弃光的条件下，利用配电网安全域边界的超平面表达式计算分布式电源最大装机容量。受节点1 的电压上限约束，节点i的分布式电源最大装机容量为

利用受配电网中N个节点的电压上限和下限约束，可得2N个节点i的分布式电源最大装机容量分别为受节点N的电压上限和下限约束第i个节点分布式电源最大装机容量。因此在电压安全约束下，节点i的分布式电源最大装机容量为

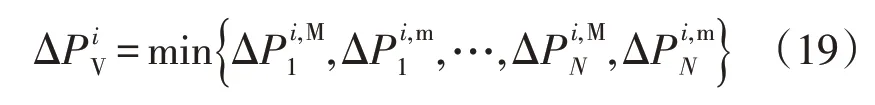
同理，由受配电网中线路的热稳定安全约束，可得节点i的分布式电源最大装机容量，故同时受热稳定安全约束和电压约束时节点i的分布式电源最大装机容量可表示为

（2）筛选分布式电源的并网位置，并向这些并网节点分配配额容量。计算每个节点的分布式电源最大装机容量，得到集合{ΔP1,ΔP2,…,ΔPi,…,ΔPN} ；根据配电网中N个节点的安装场地、配电网中分布式电源的并网节点数量等约束，按照ΔPi由大到小的顺序选择满足工程要求的Nint个并网节点。

对于某个被选定的分布式电源并网节点i，初始方案中分布式电源装机容量为

根据本文的分布式电源经济消纳原理，允许对有源配电网中的分布式电源采取弃风、弃光措施，所以实现经济消纳的分布式电源配置方案与式（21）存在差异。根据边际效应原理，当Nint个并网节点的弃风、弃光比例相等时，系统实现对分布式电源的最佳配置。

3 算例分析

3.1 评估参数

本文对IEEE 33节点配电网系统[21]开展分布式电源优化配置，默认配电网络为均一网，每段线路的最大容量为系统总负荷量；母线处的电压水平保持1.05 p.u.，其余节点的电压上、下限分别为1.05 p.u.和0.95 p.u.；在运行仿真中每个节点的时序负荷曲线采用IEEE 可靠性测试系统RTS（Reliability Test System）的推荐数据；考虑到光伏设备更容易接入配电网，本文的分布式电源主要考虑分布式光伏，光伏系统的夏季、冬季和春秋季节的典型日发电曲线和月度的发电量如图1所示。

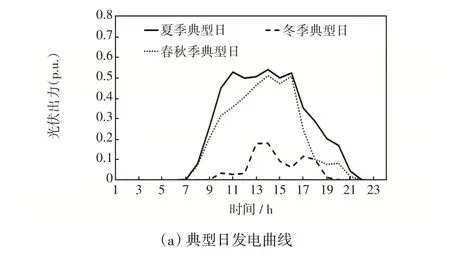
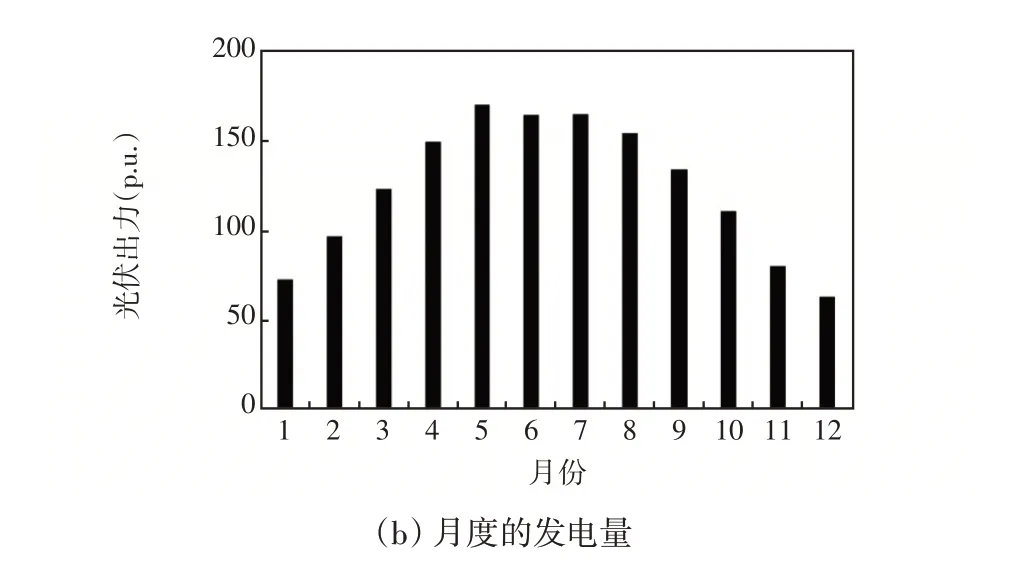
图1 典型日光伏发电曲线以及月度的发电量Fig.1 Typical daily PV power generation curve and monthly PV power generation

3.2 有源配电网最优潮流结果分析

所有节点电压安全域和热稳定安全域的交集即为配电网安全域，在安全域内的运行点满足静态安全约束；在安全域外的运行点存在越限，必须通过弃风、弃光等措施把系统运行点拉回到安全域内部。以第1 d 第12 h 的系统状态为例，经验证此时共有26 个节点的电压越上限，利用本文的最优潮流模型，可制定系统的最优弃风、弃光方案，弃风、弃光前后各节点的分布式电源出力如图2 所示。由图2可以看出该时段各节点的弃风、弃光比例分别为39.03%、94.27%、0.00%、49.49%及0.00%，系统的弃风、弃光比例为43.92%。

为了验证安全域算法的有效性，使用粒子群优化算法[12]、新的小偷与警察算法[13]和差分进化算法[14]进行验证。图2 给出了制定的弃风、弃光方案，由图2可知，本文提出的方法得到的风电和光伏功率削减方案略优于启发式算法。这是因为本文的线性优化模型可以得到严格的最优解。此外，启发式算法需要反复进行潮流计算，其收敛曲线如图3所示。

图2 各个节点的光伏电量弃置方案Fig.2 PV power curtailment scheme for each node

3.3 分布式电源经济消纳方案制定

1）初始方案的制定

根据分布式电源初始配置方案制定方法，可由系统当前运行点的裕度信息计算每个节点的最大分布式电源装机容量，运行点的选择将影响初始方案的制定。由于本文对电源配置方案开展时序运行仿真，可选择系统峰值负荷作为最大负荷运行点；选择系统的低谷负荷作为最小负荷运行点；选择分布式光伏出力与负荷比值最大的时间点。分别评估3 种运行点对应的分布式电源最大装机容量，评估结果如图4所示。

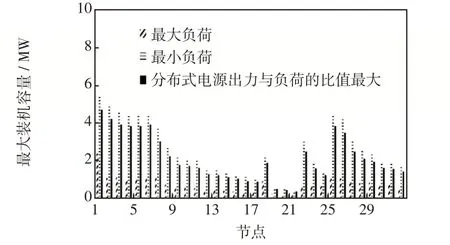
图4 各节点最大装机容量评估结果Fig.4 Evaluation results of maximum installed capacity at each node

为了不失一般性，假设根据安装场地等约束条件，选择在节点7、11、14、29 和节点31 安装分布式电源；选取图7中分布式光伏出力与负荷比值最大的时间点的评估结果作为该节点的分布式电源最大装机容量，可得5个节点的分布式电源容量比例系数，当给定配电网的分布式电源配额容量时，各节点的分布式电源初始配置方案如表1所示。

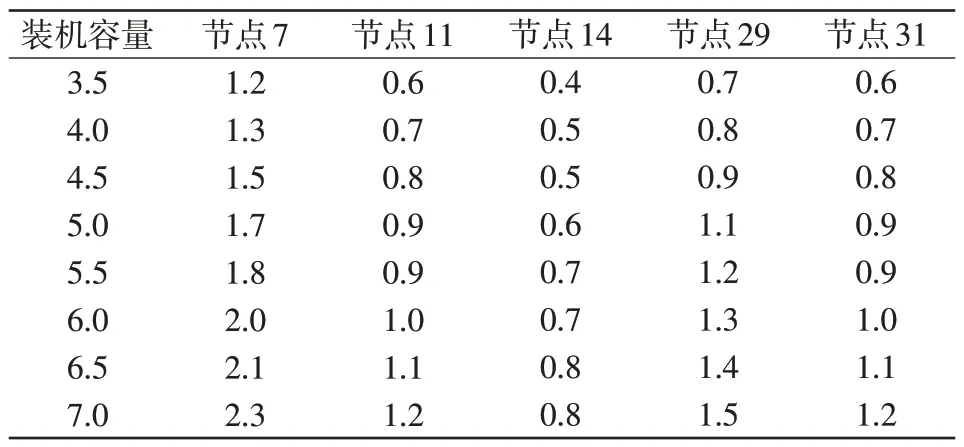
表1 优化配置初始方案Tab.1 Proportion coefficient of initial scheme for optimal allocation MW

2）等弃风、弃光比例下的配置效果

根据等比例弃风、弃光原则，对表1 中的初始配置方案进行逐步调整，可得表2中的优化配置方案。以配额容量为7.0 MW 为例，分布式电源的配置方案为节点7安装2.0 MW、节点11安装0.9 MW、节点14 安装0.8 MW、节点29 安装3.0 MW、节点31安装0.4 MW，此时系统的弃风、弃光比例为26.80%。如果采用等容量安装策略，每个节点的分布式电源装机容量将均为1.4 MW，作为对比算例，表2给出了等弃风、弃光比例和等容量安装供电效果对比。由表2 可以看出，如果按照等容量安装，由于各个节点对于光伏电量的消纳效果存在差异，会使系统的弃风、弃光电量增多，系统的供电成本升高。

表2 等弃风弃光比例、等容量安装供电效果对比Tab.2 Comparison of power supply effect between equal wind and PV curtailment ratio installation and equal capacity installation

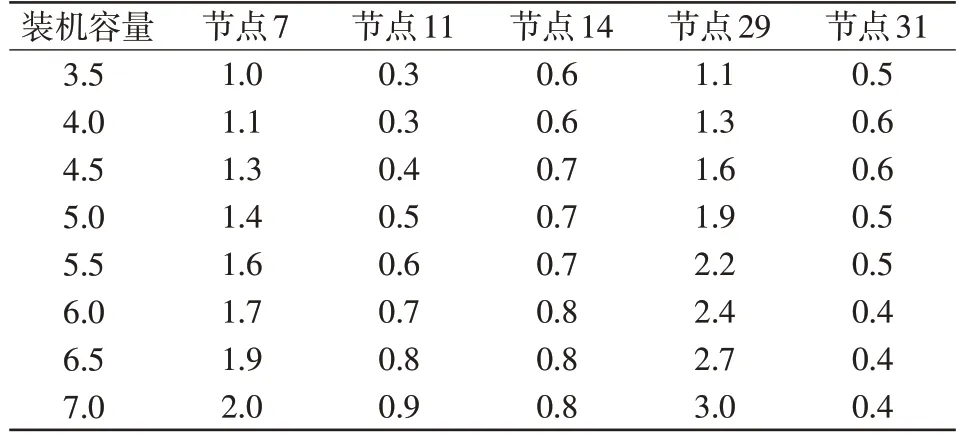
表3 分布式电源配置方案Tab.3 Allocation scheme for distributed generations MW

4 结论

面向分布式电源广泛接入配电网的发展趋势，本文提出一种基于主动配电网时序最优潮流分析的分布式电源优化配置方法。其特点是允许分布式电源弃置部分尖峰出力，通过供电经济性指标确定分布式电源的配置方案，把配网安全域引入模型的初始解制定过程和最优潮流的求解过程，实现了模型的快速求解。利用本文的优化模型和求解方法对IEEE 33 节点系统开展运行仿真，根据评估结果可以得出如下结论：

（1）利用配网安全域方法可以显著提高配电系统的仿真速度，制定更科学的弃风、弃光方案；

（2）通过采取合理的弃风、弃光措施，能够在提高配电网风光、电能渗透率的同时，降低系统的平均供电成本。