公共走廊中埋地管道交流干扰缓解措施的粒子群优化

罗兵，黄万里，党锦泽，王婷婷，罗勇芬，贾磊，王国利，廖一帆

(1. 南方电网科学研究院，广州 510663；2. 特高压工程技术(昆明、广州)国家工程实验室，广州 510663；3. 西安交通大学电气学院，西安 710049)

0 引言

油气管道邻近高压交流输电线路时受到电磁干扰可导致管道发生额外腐蚀，当干扰很大时，还可能导致管道设备无法正常工作或危及人员安全等问题[1 - 5]。然而由于周边环境限制、征地困难且成本急剧增大等，常常难以通过地理空间避让来消除这种干扰，迫使线路与埋地管道共用走廊甚至交叉跨越的情况不断增加[6 - 13]。因此，采取合理的防护措施是保证管道安全稳定运行的优选途径。

地下金属管道的交流干扰防护主要从两个方面采取措施：1)改变管道分布参数电路中感应电动势的值，实际包括管道路径上远离干扰源、沿着管道敷设导体进行电屏蔽等；2)改变管道电路的串联阻抗和并联导纳的值来改变管道感应电压电流分布，实际包括对管道接地排流、安装绝缘法兰进行电隔离等[14]。Nagat M. K.等采用极化电池作为接地排流方式，以试错法的方式确定接地系统设计方案，对一个500 kV交流线路-管道走廊进行了交流干扰防护[15]。周国雨设计了裸铜带与集中接地网相组合的防护方案，对比了防护前后管道感应电压的变化[16]。还有一些研究工作提出了有效的防护措施方案[17 - 18]，但没有详细给出依据或有待实践验证。

工程实际中主要对管道进行排流防护改造，排流点的确定多采用试错法，即在管道感应电压或电流密度超出限值的峰值处采取接地排流等防护，排流设施的安装可能会改变管道沿线的管地干扰电压分布，造成排流点远处的管地电位升高，若没有达到标准则继续在新的峰值处增加防护措施，直到所有区段满足防护限值为止。由于管道感应电压分布受管道等效电路拓扑结构和感应电动势影响很大，新增的排流点改变了管道原有的电路拓扑结构，多个排流点之间存在防护配合问题，峰值防护的试错法往往不是最优解，不易事先控制预算，而且对多种防护措施协同配合问题无从下手，在工程实际中具有较大的改进空间。

本文在研究稳态和暂态的交流输电线路对埋地管道影响的基础上[19 - 20]，继续对管道防护措施开展优化研究。建立管道分布参数电路中固态去耦合器排流装置和绝缘法兰的等效电路模块；分析土壤电阻率均匀性、接地极屏蔽效应和接地电阻以及其他地理限制因素对管道防护粒子群算法优化的影响；考虑多种因素下进行多种防护措施的组合优化；对比管道防护中PSO算法与试错法的应用；以乌兰公共走廊作为案例，采用粒子群优化正常运行时的交流干扰缓解措施。

1 理论基础

1.1 管道与防护措施的系统建模

为了计算感应电动势作用下埋地管道的感应电压电流分布，建立了基于传输线理论的管道分布参数等效电路[19,21]，该模型适用于与大地形成回路的金属导体，包括埋地管道、电缆和铁轨等。管道等效电路见图1，管道x处分段长度为dx的电路单元如图中右侧蓝色虚线框内所示。

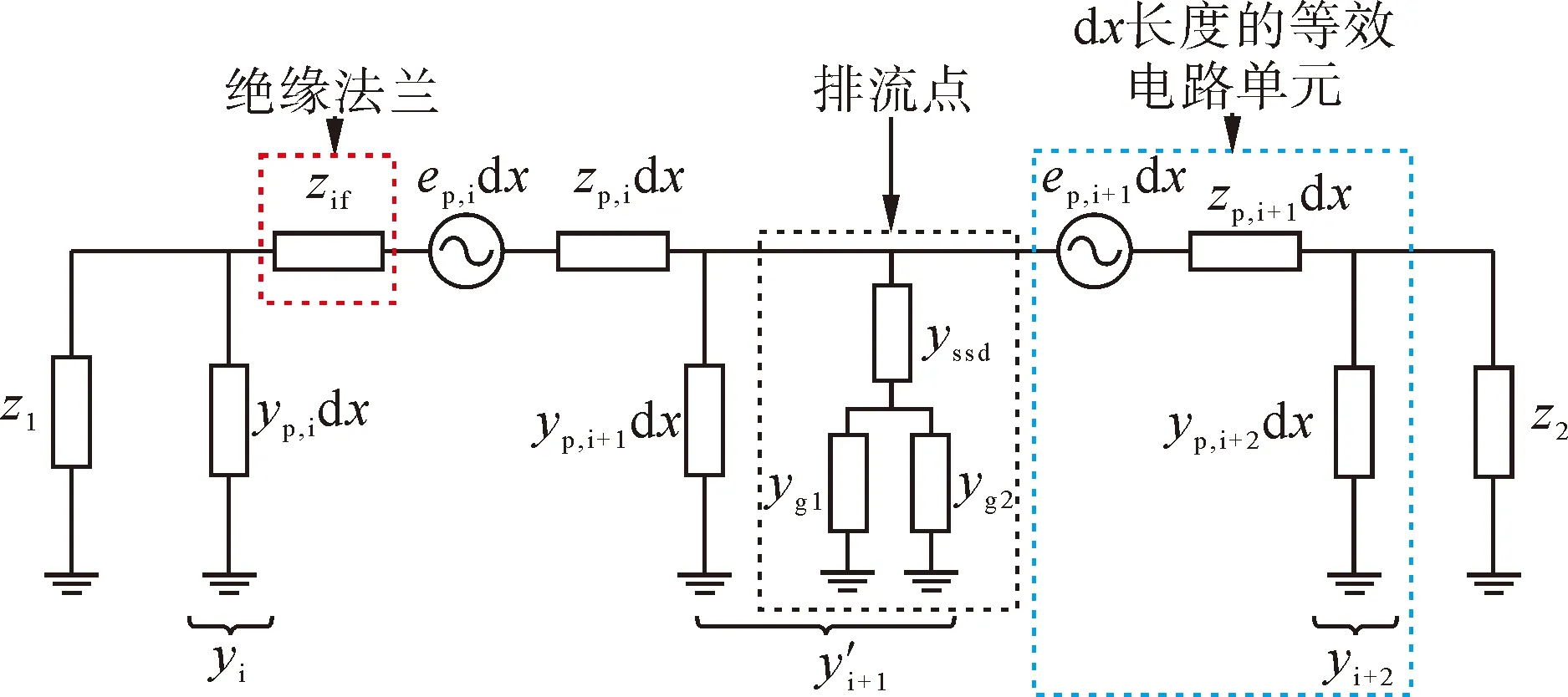
图1 有排流装置和绝缘法兰的埋地管道等效电路模型Fig.1 Equivalent circuit of buried pipeline with drainage device & insulating flange

对应的传输线方程为：

(1)

式中：u(x)和i(x)分别为管道x处的电压和电流，A；zp为管地等效电路的单位长度阻抗， Ω/m；yp为管地等效电路的单位长度对地导纳，1/(Ω·m)；ep为单位长度管道对输电线的感应电动势，V/m；z1、z2分别为管道两端的边界阻抗。

由式(1)对x求导，得到感应电压二阶微分方程：

d2u(x)/dx2-γ2u(x)-dep(x)/dx=0

(2)

阻抗zp和导纳yp由式(3)—(4)计算。

(3)

yp=πD/(ρcδc)+jωε0εrπD/δc

(4)

式中：rp为管道的电阻率，Ω·m；m0为空气的磁导率；mr为管道的相对磁导率；D为管道的直径，m；r为土壤电阻率，Ω·m；rc为防护层的电阻率，Ω·m；dc为防护层厚度，m；e0为空气的介电常数；er为管道防护层的相对介电常数。

1.2 固态去耦合器的等效电路

固态去耦合器由电容、二极管、浪涌保护装置组成，电路原理图见图2。电容用于稳态下的交流干扰排流；二极管隔直避免阴极保护电流流失，也可以用于暂态电流泄流并钳制暂态电压升高；浪涌保护器为气体放电管，用于如雷电流等高幅值电流的排流[22]。当固态去耦合器一端与管道相连，另一端连接左右两根与管道并行敷设的裸铜线时，相当于管道对地导纳并联了一个数值较大的导纳，管道采用的分布参数传输线等效电路变化为如图1黑色虚线框所示，图中yssd为固态去耦合器的等效导纳，yg1、yg2为与去耦合器相连的接地极的等效导纳。这改变了管道原有的电路拓扑结构，从而影响管道各节点的感应电压电流分布，实现缓解交流干扰的效果。

图2 固态去耦合器电路结构图Fig.2 Solid-state decoupler circuit structure diagram

1.3 基于粒子群优化理论的管道防护配置算法

近年来在电力行业的科学研究与工程实践等领域出现了大量的优化问题，智能群体优化算法在解决现代优化问题中发挥了重要的作用。粒子群算法作为智能群体优化算法的重要代表之一，在电力系统中已得到应用，但是在能源输送公共走廊的规划设计、防护优化方面的研究未见报道。

粒子群的基本数学模型为：假设存在某个N维的目标搜索空间，由m个粒子构成种群X=(x1,…,xi,…,xm)， 该种群中粒子i的坐标位置可表示为一个N维向量xi=(xi1,xi2,…,xiN,)T， 其对应的飞行速度为Vi=(vi1,vi2, …,viN)T。 粒子i目前搜索到的最优坐标位置为个体极值pi=(pi1,pi2, …,piN)T， 群体最优位置即全局极值为gbest=(pg1,pg2, …,pgN)T。 在搜索最优值pi和gbest时，粒子xi按式(5)、(6)改变自身的速度和位置[23 - 24]。

vij(t+1)=w·vij(t)+c1r1(t)(pij(t)-xij(t))+
c2r2(t)(pgj(t)-xij(t))

(5)

xij(t+1)=xij(t)+vij(t+1)

(6)

式中：j=1,2,…,N，i=1,2,…,m；t为当前迭代数；r1、r2为在[0，1]区间内的随机数，用于增加粒子的随机性；c1、c2为加速常数，也称学习因子，用于调整全局最优粒子和个体最优粒子搜索方向的最大速度；w为惯性权重。

w用于改善算法收敛性，调整w值可以权衡局部和全局的搜索能力。传统PSO采用线性递减权值策略，与粒子适应度不匹配。为加强局部与全局搜索协同性，本文采用自适应惯性权重如式(7)所示。

(7)

式中：fi为粒子i的适应度，fav、fmin分别为群体适应度的均值和最小值；wmax、wmin分别为最大最小惯性权重，一般取0.9和0.4。

1)目标函数

管道防护措施优化目标为使防护的总成本达到最低。假设管道分为a个可防护的节点，对于某项防护措施建立一个a维的列向量，里面的元素为该节点采取这项防护措施包含设备、施工、运输、停运等费用后归一化的成本。当考虑的防护措施有b类时，组成防护措施系数矩阵Ma×b， 优化目标为：

(8)

式中mij为矩阵元素。由式(1)对应的节点电压和环路电流方程组，计算不同节点和路径上的电压电流，采用防护措施时，方程组中的系数根据图1中的结构进行修正。

2)约束条件

主要考虑输电线路稳态运行下，管道、人员、设备的安全限值作为计算的约束条件如式(9)所示。

(9)

式中：Ui为节点i的感应电压；ρi为环路i的视在土壤电阻率；Uf为装有阴极保护、测量等设备的特定位置的感应电压。如果有特殊的防护要求可以增加特定约束。

优化算法基于种群和搜索的概念，通过各个粒子间的竞争与合作，实现复杂空间上最优解的搜索。

2 管道防护系统优化分析

为使模型更加接近工程实际，需要考虑多种因素下的管道防护优化，本文以一个典型的接近-跨越-并行-远离的公共走廊进行研究，公共走廊路径示意图如图3所示，管道起点与终点经小电阻良好接地，线路与管道的系统参数按1.1节中的线路与埋地管道进行计算。

图3 公共走廊线路管道路径俯视图Fig.3 Top view of power line& buried-pipeline in common corridor

2.1 考虑土壤电阻率均匀性的防护措施优化

土壤电阻率及其分布对防护措施存在影响，因此分3种工况研究：工况1的土壤电阻率为恒定值；工况2为管道由较低土壤电阻率区进入较高土壤电阻率区；工况3为公共走廊中部为较低土壤电阻率区，两侧为较高土壤电阻率区。

另外，管道分段长度越小，防护点位置越精确，但计算复杂度随之增加，综合考虑管道分段长度约为110 m。

研究假设线路正常运行时相电流为1 000 A，单根裸铜带等效半径0.01 m，长度100 m，埋深1.9 m。

1)工况1

公共走廊内的土壤电阻率假设为100 W·m。单个排流装置及其接地极视为一个单位防护成本，在满足安全限值约束情况下，对管道防护措施进行了粒子群优化计算。粒子群的种群大小为350；权衡粒子个体认知能力和群体协调经验，学习因子c1、c2分别取1.6和1.8；惯性权重采用自适应方法，权重上下限wmax、wmin取0.95和0.6。

管道采取防护措施前后的管地电位计算值如图4(a)所示，按腐蚀最严重情况考虑的管道交流电流密度的计算结果见图4(b)。

图4 考虑土壤电阻率的管道防护PSOFig.4 PSO of pipeline protection considering soil resistivity

由图可知，无防护情况下，公共走廊内管道感应电压在线路管道邻近点和交叉跨越点处存在21.68 V和16.18 V两个极大值；两个极大值附近分别有5.23 km和1.44 km范围的管道受到中等程度的交流干扰。经过PSO算法防护优化后，公共走廊内的管道所受电磁影响大幅减小，降为弱交流干扰。

为评估交流干扰电压对管道腐蚀的影响，我国在GB/T50698—2011《埋地钢质管道交流干扰防护技术标准》[25]对交流干扰程度进行了评估，其中规定，管道的交流干扰电压有效值的平均值不超过4 V时，不需要采用交流干扰缓解措施；大于4 V时，由式(10)计算交流电流密度JAC进行评定。

(10)

式中：JAC为管道涂层破损点处的交流电流密度，A/m2；UAC为管道交流干扰电压有效值的平均值，V；ρ为研究点处与埋地管道相同深度的土壤电阻率的测量值；d为涂层破损点直径，一般认为管道金属裸露面积100 mm2时最易发生交流腐蚀，式(10)中d值按腐蚀最严重情况取0.011 3 m。

在均匀土壤电阻率情况下，根据式(10)计算得的交流电流密度与管地电位分布趋势一致，此时优化得到的最少排流防护点为3个，与管道起点距离分别为4.29 km、7.16 km和10.23 km。PSO算法初值随机生成，经过19次迭代后收敛得到最优结果。

2)工况2

工程实际中，对于一个地理跨度较大的公共走廊，管道沿线各处的土壤电阻率是不均匀分布的，这将影响管道自身的等效串联阻抗和并联导纳，以及排流装置接地极的接地电阻值等，使得PSO算法的优化结果存在变化。

假设土壤电阻率沿管道路径变化，采用Perlin噪声函数随机生成垂直分层土壤电阻率。Perlin噪声属于梯度噪声，相比随机数值噪声(如白噪声)，基于分形算法的Perlin噪声函数更准确地模拟如云层、地形等自然环境参数的分布特性[26]。这里工况2的土壤电阻率的分布规律为管道由较低土壤电阻率区进入较高土壤电阻率区，如图5(a)所示。

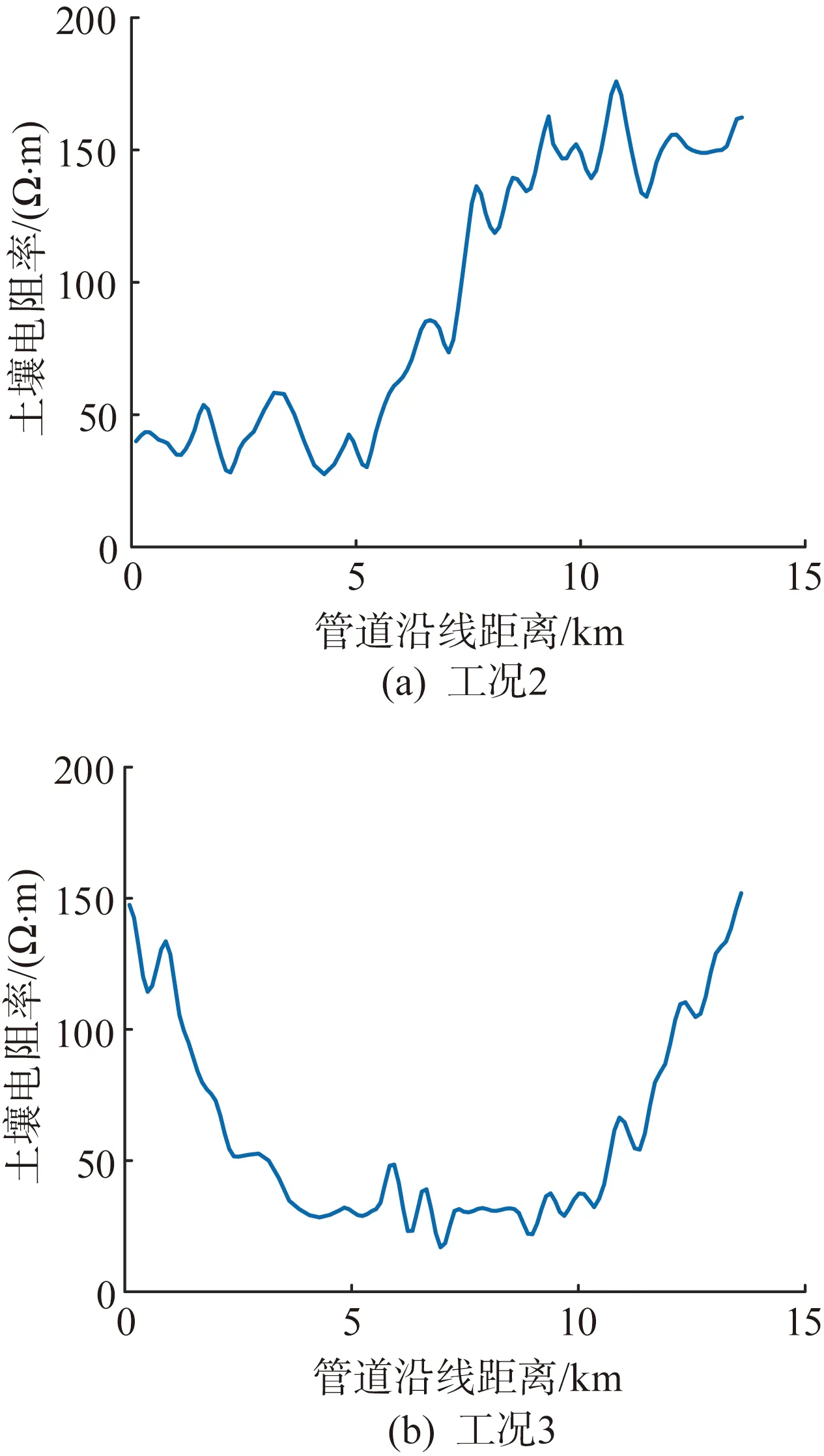
图5 Perlin随机噪声器产生的土壤电阻率分布Fig.5 Soil resistivity distribution generated by Perlin random noise

对工况2的管道PSO防护优化计算结果见图4(c)和(d)。由于管道在ρ较低区段因涂层损坏发生交流腐蚀的风险更大，需要采取较多排流点保证沿线的管道感应电压处于较低值；ρ较高区段则很容易达到防护要求。不过感应电压峰值的允许值比ρ较低区高，但未超过相关限值，不会对人身安全和设备抗工频干扰正常工作造成影响，ρ较高区段和ρ较低区段的排流点个数分别为1、3。从前两种工况也可以看出交叉跨越的电磁影响比邻近点更强，需要更多防护。PSO算法经过27次迭代后收敛。

3)工况3

工况3的土壤电阻率的分布规律为：公共走廊中部为较低土壤电阻率区，两侧为较高土壤电阻率区，见图5(b)。

对这种工况的管道PSO防护优化计算结果见图4(e)和(f)。这种情况下强干扰区土壤电阻率低，一旦管道涂层破损，由于接地电阻较低，破损处可产生高幅值交流电流引发强交流腐蚀，因此需要大量排流点保证感应电压处于较低水平，管道-线路交叉点、并行和远离点附近区段分别需要2、2和3处排流点，以保证达到安全限值，从发生交流腐蚀风险的角度考虑，线路不宜与管道在土壤电阻率过低的公共走廊并行。PSO算法经过57迭代后得出最优结果，排流点越多，算法收敛所需的计算时间越长。

2.2 考虑接地极对管道屏蔽效应的防护措施优化

由于排流点接地极导体沿管道平行敷设，接地极流过电流产生磁场影响附近埋地管道金属部分的感应电动势，也就是图1中yg1和yg2流过的电流对管道上的ep,i和ep,i+1产生影响，排流点位置除了改变管道的电路拓扑结构，还改变了环路单元上的参数值，以下将对这种情况下的PSO防护优化进行研究。

地下平行导体的大地返回互阻抗Zm与自阻抗Zs可采用Pollaczek公式计算，但该公式中含有强振荡性的积分项，计算过于复杂。因此一般采用该公式的近似表达式进行计算，如式(11)—(12)所示。

(11)

(12)

式中：μ0=4π×10-7H/m，为真空磁导率；g=1.781 1，为欧拉常数；ρ为土壤电阻率，W·m；d为两个导体之间的几何距离，m；r为导体半径，m；R为导体单位长度电阻，W·m。

对于沿管道平行敷设的裸导体而言，屏蔽因子k可以用式(13)计算[12]：

(13)

式中：Zp4、Z44分别为管道和屏蔽导体之间的互阻抗、屏蔽导体的自阻抗，由式(11)和(12)计算。

以工况3的土壤电阻率分布为例，计算管道PSO防护优化，计算结果见图6。

图6 考虑接地极屏蔽效应时管道PSO防护Fig.6 PSO of pipeline protection considering shielding effect of earthing pole

管道在安装排流装置时，如果接地极选择平行于管道敷设的裸导体，接地极的屏蔽效应削弱了干扰源在管道上产生的感应电动势，带来额外的防护效果。与图4(e)和(f)中的结果对比，在满足交流腐蚀限值的情况下，交叉点附近的排流点减少了一个，排流点总数由7降至了6，对应的位置也有所变化，见表1。相比采用接地网或阳极床等集中接地排流，更推荐采用排流接地极平行与管道敷设的方式，特别是在线路-管道邻近或交叉跨越等存在较强电磁影响区域。

表1 考虑屏蔽效应前后的PSO优化的排流点与起点的距离Tab.1 Distance between starting point and current drainage positions before and after PSO considering shielding effectkm

2.3 接地极接地电阻对防护效果的影响

在某些情况下固态去耦合器的接地极因成本或者地形地势因素，无法与管道并行敷设，只能采取接地网或者阳极地床集中接地排流时，此时的防护措施优化将有所不同。接地极接地电阻大小直接影响排流点的排流效果，以下研究不同接地电阻的接地极对PSO防护优化的影响。

线路正常运行电流1 000 A，土壤电阻率分布为工况2时，接地极接地电阻值分别为2 Ω和4 Ω时的PSO优化计算结果见图7。

图7 不同接地电阻时的管道防护PSOFig.7 PSO of pipeline protection under different earthing resistances

使管道所有区段降低至弱交流干扰，3种不同接地电阻情况下所需要的排流点分别为9和19个。随着接地极接地电阻升高，排流效果快速减弱，需要更多的排流点以更加密集的方式集中于强干扰区进行排流。当接地电阻大于9.1 Ω时，仅凭排流方式难以将电磁影响降低至弱交流干扰，接地电阻大小对排流点数量影响很大，在实际应用时应尽可能减小以增加缓解效果。

2.4 多种防护措施配合下的粒子群优化

接地排流可以缓解大部分情况的交流干扰，但是当公共走廊内的线路与管道距离过近、线路负荷较大或者接地极接地电阻无法降低时，管道受到的交流干扰可能无法单纯凭借排流法缓解，这时需要采取额外的防护措施，不同防护措施的配合和规划也是一个优化问题。

管道分段隔离法(绝缘法兰，见图1左侧红色虚线框)在防护强交流干扰时具有很明显的效果，通过绝缘法兰将管道电气绝缘，在强交流干扰区阻断了感应电动势和感应电流的多段叠加。但是在已经投运的管道上改造难度和成本较大，一般在管道设计阶段或者其他防护措施达不到效果时采用。

以工况2下的土壤电阻率分布为例，绝缘法兰的电阻值取50 MΩ[21,26]，当排流点接地极接地电阻取9.1 Ω，此时排流点缓解效果较差，仅靠排流法难以将所有区段的电磁干扰降低至弱交流干扰水平。采用PSO算法对管道排流和分段绝缘进行组合优化计算，当绝缘法兰与排流点的防护成本比值分别为5和10时，PSO算法的计算结果如图8所示。

图8 组合不同管道防护措施的PSOFig.8 PSO of combined protection measures for pipeline

在单种交流干扰缓解措施难以满足防护限值要求时，PSO算法可以实现不同措施的组合优化问题。由该图看出，绝缘法兰作为串联在管道分布参数电路模型中的大阻抗，阻断了管道串联方向的感应电动势叠加和感应电流通路，管地电位幅值/交流泄漏电流密度在绝缘法兰处达到极大值后停止上升，另一侧则从另一个极大值开始逐步下降，两个绝缘法兰之间的管道区段的管地电位幅值近似呈“V”形分布。一般来说，由于两个法兰中间的管地电位幅值较低，对于简单的情况，可以考虑绝缘法兰以管地电位峰值处为中心对称设置绝缘法兰，最大程度地降低管地电位，但是绝缘法兰改变了管道电路拓扑结构，可能会导致远处其他地方的管地电位升高，与排流法组合时模型更加复杂，此时采用PSO算法进行优化计算，可以搜索得到绝缘法兰和排流装置在管道沿线组合防护点的最优解。

绝缘法兰具有很强的交流干扰防护效果，当绝缘法兰与排流装置的防护成本比值较低时，PSO算法更倾向于采用绝缘法兰进行多个分段绝缘来抑制交流干扰水平；绝缘法兰的防护成本升高时，PSO算法倾向于减小绝缘法兰数量，在不同位置采用更多的排流点来配合绝缘法兰降低交流干扰。

2.5 考虑其他限制因素下的防护措施优化

防护措施的优化除了要考虑上述不同因素对排流防护效果的影响，还需考虑到其他因素对防护成本的影响，以下分析几个特殊限制因素。

1)复杂地形系数Ct=(ct1,ct2, …,ctD)T

管道的输送路径可能经过例如陡坡、山林、岩石带等。这些因素使得安装防护措施时带来额外的施工成本，根据具体情况采用复杂地形系数Ct修正，防护系数矩阵内某种措施的列向量每个元素与Ct中对应位置的元素相乘后得到防护成本修正值。

2)土地属性系数Ce=(ce1,ce2, …,ceD)T

管道的输送路径可能经过一些经济作物带例如农田、牧场等。在青海的一个案例中，对管道运维监测记录调研中发现有些检测数据缺失，原因是测试桩位于不易进入和采取防护措施的农场区域。根据具体情况采用土地属性系数Ce修正。

3)特殊地理系数Cs=(cs1,cs2, …,csD)T

管道的输送路径可能经过一些特殊地理区段如穿过河流水域、钻越交通道路、架空穿过峡谷等。这些地点的接地防护措施施工困难或者无法施工。根据具体情况采用特殊地理系数Cs修正。

假设公共走廊内的地理因素按图3分布，土壤电阻率分布取工况3，管道由较高土壤电阻率区进入较低区；假设上述3种系数分别为2、1.8和10，管道的PSO防护优化结果如图9所示。

从图9(b)中可以看出，排流点的搜索倾向于避开山地、田地等增加防护成本的区域，在满足限值的情况下，此时的PSO防护优化计算的排流点数量为7个，相比图4(e)和(f)中的情况额外增加了1个，但是总体防护成本减少了11.4%。

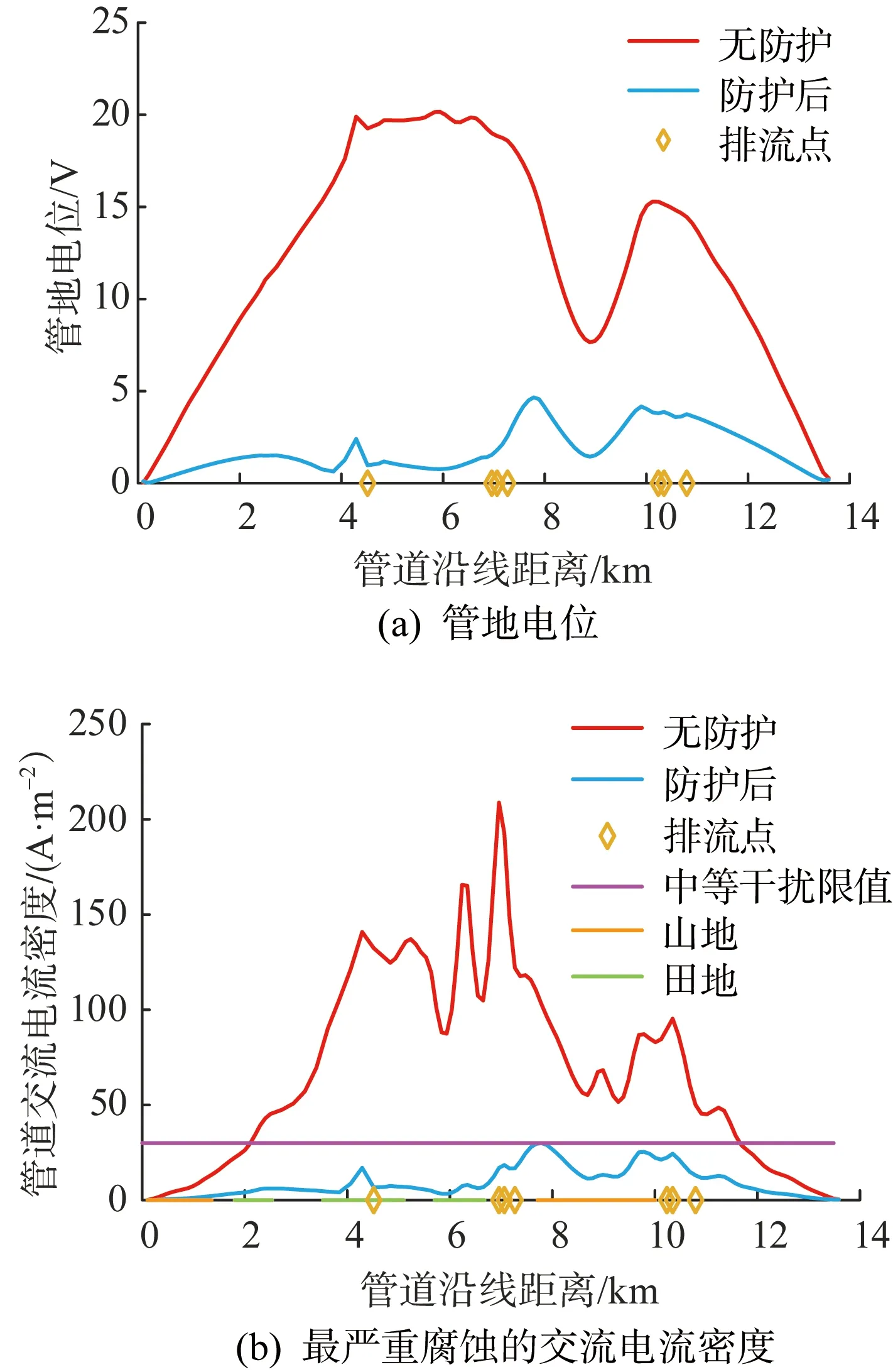
图9 考虑其他限制因素时管道PSO防护Fig.9 PSO of protection measures for pipeline considering other limiting factors

3 粒子群算法与试错法的对比

对于排流点的规划和设计，目前工程实际中最常用的是试错法(误差尝试法)。即在管道感应电压最高点(或者交流电流密度计算值最大处)设置排流点，排流点改变了电路拓扑结构可能导致远处管道感应电压升高，若超过限值要求，则在新的最大值处增加措施；若某处交流干扰较强，单个排流点无法使该点降低至限值以下时，在邻近区域继续增加排流点，直到满足要求为止。由于管道感应电压电流分布受管道电路拓扑结构和感应电动势影响很大，试错法往往难以在多数情况下取得最优。以下研究不同程度的电磁影响、不同排流效果下PSO算法和试错法的对比。

当公共走廊内的管道排流点效果不变时，假设接地极接地电阻为1 Ω，土壤电阻率按工况2分布，研究线路负荷电流在500～1 800 A范围时的PSO算法和试错法的效果对比，如图10所示。

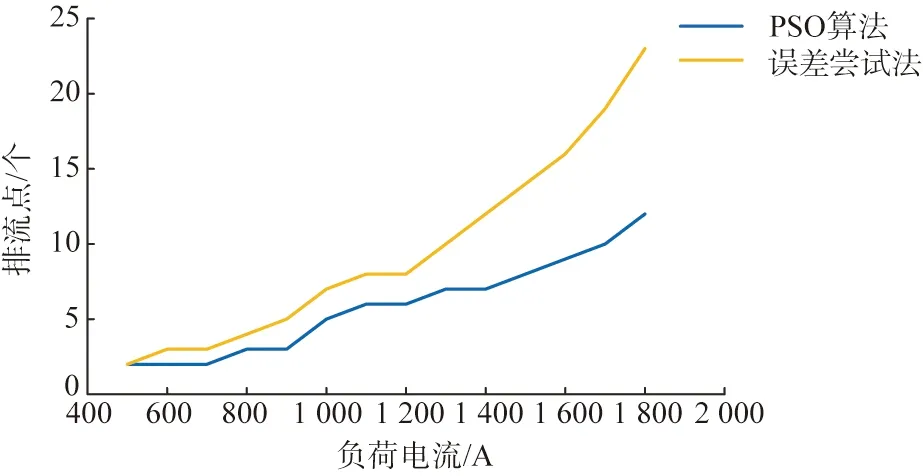
图10 考虑线路负荷电流时管道需要的排流点数对比Fig.10 Comparison of pipeline drainage numbers required with line current

从图中可以看出，当公共走廊内的线路运行电流小于500 A时，因为电力负荷较小，线路对管道的电磁影响较低，排流点比较容易达到缓解效果，具有较大的裕度，这种情况下可以进行排流效果的进一步优化，即在给定排流点数量基础上使沿线交流干扰尽可能减弱；随着负荷升高，两种方法需要的排流点数量逐步升高，在线路负荷电流大于1 200 A后，试错法需要的排流点数量快速增加，由于PSO算法能够搜索空间中更优的排流点位置，实现各个点之间的排流配合，在电磁影响较强的公共走廊内具有更大的优势。

对公共走廊中其他影响因素，如接地极的接地电阻等，对比研究均表明，无论从排流点的数量，还是位置设置，以及总体排流效果，PSO算法对管道防护上有更明显的优化效果。

此外，基于PSO算法的管道防护优化方法是模块化的，可以进行横向、纵向、高维拓展等改进。横向上，若某种防护措施能等效为管道分布参数模型的某个模块，PSO算法可以实现多种防护措施的组合优化问题，而传统的试错法难以用于此类问题的分析；纵向上，PSO算法可以引入精英系统、其他算法的核函数等模块来改进，增强算法的收敛速度和寻优能力，且可根据工程实际考虑多种因素和机理，使优化分析过程更适用于实际情况；PSO算法的搜索空间从一维拓展到二维时，可以实现对管道、线路等坐标路径的寻优，在权衡建设与防护的经济性、电磁影响等方面，为能源输送公共走廊内的电磁兼容优化问题提供设计与规划上的帮助。

4 工程实例分析

以青海乌兰公共走廊为案例研究走廊内750 kV、330 kV线路正常运行时的交流干扰缓解措施的PSO优化问题。公共走廊的路径信息如图11所示。

图11 乌兰公共走廊路径俯视示意图Fig.11 Top view of Wulan common corridor

各线路正常运行电流以及线路管道参数由表2给出，排流方式采用固态去耦合器连接裸铜带接地，裸铜带与管道并行敷设，单根裸铜带等效半径为0.01 m，长度为100 m，埋深为1.9 m。

表2 各交流输电线路稳态正常运行相电流Tab.2 Steady-state normal operating phase current of each AC transmission line

管道的PSO防护和试错法防护设计的优化结果见图12，各线路正常运行时，管道在交叉跨越点附近有4.3 km区段受到中等交流干扰，PSO法将交流干扰程度降低为弱需要两个排流点，与起点阀室距离分别为61.52、66.97 km；试错法的排流点位置分别为61.52、65.95 km。线路-管道交叉区干扰程度不高，两种方法需要的排流点数量一样，但是PSO算法防护后交流电流密度最大值为15.13 A/m2，试错法为21.08 A/m2，PSO算法搜索的排流点位置能取得更好的干扰缓解效果，在应对公共走廊未来新建线路或负荷增长时具有更大的防护裕度。经过排流后交叉点附近区段的交流干扰大幅下降，但会导致上游部分区段的管地电位有所升高。

图12 乌兰公共走廊内管道PSO防护优化Fig.12 PSO of pipeline protection in Wulan common corridor

5 结论

为减轻公用走廊中交流线路对埋地管道的电磁干扰，本文对管道防护措施及优化方法进行了研究。建立了管道分布参数电路，其中包含固态去耦合器排流装置和绝缘法兰的等效电路模块。基于粒子群算法对管道防护系统进行优化，并研究了对影响管道防护措施的多种因素。结论如下。

1)土壤电阻率分布均匀性导致防护点配置存在差异，土壤电阻率较低区段发生交流腐蚀的风险较大，需较多排流点将管道电压降低至较低水平。

2)接地极与管道平行敷设时存在的屏蔽效应降低了管道上的感应电动势，可以增强防护效果。

3)排流法无法有效缓解干扰时，可采用管道绝缘分段和排流的组合优化，绝缘法兰在强干扰区域具有很明显的效果。

4)考虑了其他地理限制因素下的管道防护，增强PSO算法在权衡技术性与经济性方面的寻优能力，更接近工程实际。

5)比较了管道防护PSO算法与试错法，满足防护限值要求时，在不同程度的电磁影响和接地极排流效果下，采用前者的防护方案相比后者能节省更多防护成本，在较强交流干扰水平、较差排流效果的情况下具有更优的效果。

6)以乌兰公共走廊为案例，研究线路正常运行时的交流干扰缓解措施的优化，采用两个排流点后交叉点附近区段的交流干扰大幅下降为弱等级。