基于线性规划模型的信贷风险评估

马明宇 管淑琦 曾垂剑 潘文杰

（衢州学院 浙江衢州 324000）

1 绪论

1.1 研究背景

在经济全球化时代背景下，中小微企业逐步成为发达国家与发展中国家经济发展中的一支重要队伍。近年来，央行在制定政策时也加大了对中小微企业的扶持力度。但由于大多数中小微企业发展不完善、企业规模小、信息不对称等问题，通常很难达到银行的放贷标准。银行为了规避风险，通常从企业的供求关系、信誉等级和风险系数等多方面因素考虑提供贷款额度及利率优惠。

新冠疫情的持续对各行各业产生了不小的冲击，中小微企业受到了较大影响。为了维持中小微企业的稳定与促进其持续健康发展，银行纷纷出台各种信贷政策，协手中小微企业共渡难关。

1.2 问题提出

问题一，要求对不同企业风险进行量化，在银行信贷总额固定的情况下对123家企业给出合理策略。

问题二，要求在问题一的基础上对302家无信贷记录的企业风险定量，并在银行年信贷总额为1亿时对302家企业给出合理信贷策略。

问题三，要求企业的生产经营和经济效益在面对突发因素时对其信贷风险进行量化，通过这些突发因素对各企业的影响，给出银行信贷总额为1亿元时的调整策略。

1.3 模型假设

(1)假设银行固定信贷额度足够多，每家企业都想尽可能获取更多贷款

(2)假设题中所给发票完整，即企业进行交易活动都有发票

(3)假设负数发票都是因为退货所开，而且退货原因基本为产品问题

1.4 符号说明

i表示样本序列；j表示指标序列；r表示年收益率；q表示客户流失率；w表示利润；w′表示利润率；1C表示销售总额；C2表示进货总额；h1表示负数发票；h2表示作废发票；H表示总发票；H1表示进项总发票数H2表示销项总发票数；h′表示产品质量；h′表示发票作废率；f+表示上游企业稳定指数；f-表示下游企业稳定指数；m表示放贷额度。

2 问题分析

问题一，首先对异常数据进行预处理，以企业信誉评级和是否违规为指标，依据风险系数划分放贷等级，确定每家企业的放贷额度。其次我们通过题中所给贷款利率与客户流失率的数据，分别求解出银行收益最大时A、B、C三级企业的贷款利率。最后，联立线性方程建立最优模型求解出最优解。

问题二，我们分别计算出各企业在近两年的营业额、利润、利润率、产品合格率及发票作废率，通过这五个方面体现出企业获利能力、履约能力、信用风险和投资收益。再依据风险系数按照等分法评估企业的信用等级，依据信用等级确定企业的贷款额度与贷款利率。依据贷款额度、贷款利率与风险系数联立线性方程组。

问题三，我们以新冠疫情为例来深入分析，首先对302家企业按照所属行业进行分类。通过查找相关资料，确定在疫情影响下的各个行业平均消费变化数据，以消费水平和风险系数为指标，根据放贷系数、贷款利率与贷款额度联立线性方程组，建立优化模型求解出最优贷款策略。

3 模型建立与求解

3.1 问题一模型建立与求解

在信贷总额固定的条件下银行确定不同企业放贷策略，需要综合考虑企业的风险系数、年收益率和客户流失率的影响。利用TOPSIS优劣解距离法对风险评估作量化处理，依据风险系数将企业分为6个等级，从而确定对企业的放款额度，再确定放款年利率与客户流失率。

3.1.1 对企业风险评估进行量化，确定不同风险等级企业的放贷额度

在不考虑信誉等级与是否违规两者之间权重关系的情况下对附件1信誉等级进行赋值，将信誉评级系数定为A=4,B=3,C=2,D=1；视违规=0，未违规=1。以信誉等级和是否违规2个指标为列向量，123家企业作为行向量建立正向化矩阵X。

TOPSIS具体步骤如下：

(1)统一指标类型

由于我们给出的信誉评级和是否违规数据两个都为极大型指标(期望取值越大越好)，指标类型统一，因此可以直接进行标准化处理。

(2)标准化处理

标准化处理信誉评级和违规两个指标可以消除量纲的影响，使得到的数据更具科学性。

(3)计算得分并归一化

计算评分公式S如下：距离D-公式：

第i(i=1,2,…,123)个企业与最大值距离D+和最小值

其中，Z+为每个指标最大值，Z-为每个指标最小值。最后将得分归一化处理。

用MATLAB求解得5类放贷等级分别为a=1，b=0.8，c=0.6，d=0.4，e=0.2，f=0，银行对企业放贷额度范围在10万～100万元，根据同等比例原则对不同风险等级的企业放贷额度进行划分，结果如表1所示。

表1 不同风险等级放贷额度分配

3.1.2 建立初等模型确定年收益率客户流失率得出最优解

(1)异常数据预处理

采用拟合方法对异常数据进行修正。设附件3中的各样本点为(rk,qi)(k= 1, 2,3;i=1,2,…,123)，用EXCEL画出散点图发现两者之间成对数分布。利用MATLAB求解，设置拟合曲线由曲线系数k′为线性，在基于最小二乘法原理下的线性拟合之后得到部分修正数据。

(2)计算最优解

建立初等模型，假设客户流失率为q，客户吸引率为1-q，年收益率为r，其中，4%≤r≤15%，

用EXCEL软件求出最优解Q1=0.0401，Q2=0.0407，Q3=0.0415。参考相关文献，将银行的基础利率定为6.2%，对信誉等级A级企业降息25%，B级和C级企业降息5%(见表2)。

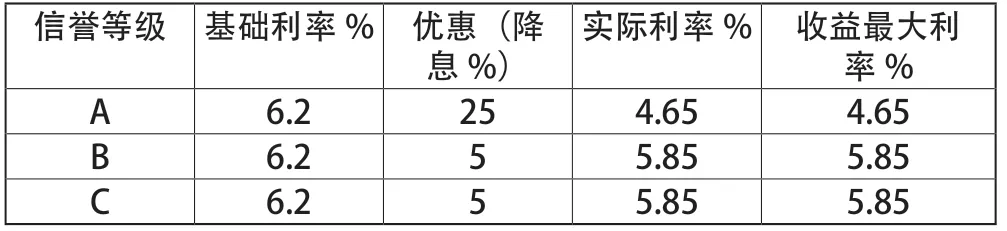
表2 不同信誉等级利率优惠表

3.1.3 最佳策略求解

综合考虑在总信贷额度一定的情况下按风险系数大小确定放贷额度，建立数学规划模型如下：

其中，321,,mmmm1，m2，m3为A、B、C三个等级根据年收益率及客户流失率分别确定的总放贷额度，M为固定总信贷额度。由于D等级全部存在违规现象，所以拒绝D等级企业贷款申请。在问题中M具体数据并未给出，因此模型可通过数据代入直接计算出结果得到最佳策略。

3.2 问题二模型建立与求解

计算出各企业近两年的营业额、利润、利润率、产品合格率、发票作废率及上下游企业稳定系数，采用熵权法求出每个指标权重，再次使用TOPSIS优劣解距离法为6个指标评分和排序，根据优惠利率做线性规划模型求出最佳策略。

3.2.1 计算影响因子权重

确定6个信用评级影响较大的因子：利润、利润率、产品合格率、营业额、发票作废率及上下游企业稳定系数。运用熵权法对这6个因子进行赋值权重。利用熵权法计算权重能深刻反映出这六个因子的区分能力，相比层次分析法更客观，具有较高的可信度。影响因子计算方法如下：

以利润、利润率、产品合格率、营业额发票作废率和上下游企业稳定因素为指标做列向量，以302家企业为研究对象做行向量构造矩阵Y。再运用熵权法求解出各因子的权重，如表3所示。

表3 各影响因子权重占比

3.2.2 利用TOPSIS将所得各指标权重进行排序处理

利用MATLAB经过正向化、标准化和归一化之后得到302家企业风险系数排序。由等分法将企业风险系数等间隔分为9类(3)，设ui(i=1,2,…,8)为对0到1取值范围内进行评价等分法的第i个分割点，U为企业风险评级中系数最大值；u为企业风险评级中系数最小值，则风险信用评级等分法的第i个分割点ui为：

最终结果如表4所示：

表4 风险等级分类及占比个数

3.2.3 建立优化模型求解最佳策略

对排序之后的302系企业归类，将aaa、aa、a风险等级归为A信誉评级，将bbb、bb、b风险等级归为B信誉等级，将ccc、cc、c风险等级归为C信誉等级。最后计算每类信誉等级平均风险系数，计算公式如下：

式(7)中：*x代表均值，x′代表样本点。最后计算得出A=0.0215，B=0.1411，C=0.1289。

综合考虑302家企业风险系数对不同信誉等级企业信贷额度的影响找到最优解：

3.3 问题三模型建立与求解

根据不同行业之间的差异将302家企业整理分成12种类型(见表5)：

表5 各行业分类数量及同比增长率

以问题二中各企业的风险系数和各行业消费水平为指标，302家企业为研究对象，建立矩阵X′。处理步骤同问题二，先对X′进行加权，利用MATLAB得到受疫情影响下的风险系数权重为0.8，消费水平为0.2。由问题一中的TOPSIS优劣解距离法计算以风险系数和消费水平为指标，以302家企业为对象的矩阵得出302家企业在疫情影响下的风险系数排序。最后通过等分法对新排序进行等级划分(见表6)：

表6 不同等级贷款额度上限

基于疫情冲击对不同行业的影响，在问题二的基础上建立新的线性方程组：

得到最终结果为：m1=1390,m2=5770,m3=2840

4 模型评价

(1)模型的优点。影响因素考虑较全面，依据因素不同加权求解风险系数较为可靠。贴近实际，响应国家号召，对中小微企业降息。

(2)模型的缺点。问题一中的信誉等级由专家给出，存在一定的主观性。对数据的处理缺少科学性，在求解利润时淡化了场地和人工影响。

(3)模型的推广和改进(横向、纵向)。在进行风险系数计算时加入固定资产等因素可以用于规模以上企业的贷款及证监会对上市公司的评估，还可以运用于企业投资。