基于决策场和动力学的航空器搜寻区域划设
李嘉铭, 邵荃
(南京航空航天大学民航学院, 南京 211106)
航空搜寻与救援是指航空器发生飞行失事或事故时,国家有关部门对航空器上人员及相关设施设备进行搜寻和救援工作。一旦发生航空器紧急情况,如何对失事航空器进行定位以确定搜寻区域对后续开展搜寻救援工作的效率极为重要,是中国搜寻能力建设亟需解决的问题。目前关于该领域的研究工作主要涉及以下3个方面。
(1)利用卫星雷达等技术获取失事航空器信息进行定位。Lukowski等[1]利用航天系统合成孔径雷达采集疑似区域卫星图像,通过图像识别方法来确认坠毁航空器具体坐标。Koester等[2]通过分析大量飞机失事事件中最后雷达位置与坠毁现场距离,得出了95%的飞机坠毁在距离最后雷达位置0.8海里(1海里=1.852 km)范围内的结论,为搜寻区域确定提供了理论依据。Dyne等[3]将搜寻专家经验与航空器失事天气状况、地形信息、飞机模型等方面知识进行统合,得到了飞机失事地点概率分布图。 Magoon[4]阐述了在航空器坠毁案例中应用历史图像、GPS等手段从而有效地定位坠机地点。史谦等[5]设计一种指示飞行器落点坐标的信标机。其可在下落过程中不断获取实时定位信息,利用北斗系统的短报文通信功能将预测的落点坐标发送回地面。
(2)借助计算机识别潜在着陆点的基础上进行可达性研究。 Coombes等[6]详细介绍了在恒定均匀风条件下确定迫降时任何可能的紧急着陆点的可达性的方法。Akametalu等[7]提出一种基于可达性的迫降系统,该系统利用汉密尔顿-雅可比-贝尔曼可达性来确定故障飞机的可行着陆区域。
(3)通过动力学建模,对航空器迫降轨迹进行模拟。孙旋[8]使用光滑粒子动力学方法研究了直升机水上迫降性能,建立了一套水上迫降计算分析方法。秦芹[9]考虑到飞机在坠落过程中受到空气气流的影响,研究了飞机在发生事故时失去动力后飞机坠落轨迹和落地点位置问题。
目前,大部分关于失事航空器搜寻范围划设的研究只停留在全知信息的前提下,单独对航空器进行运动模拟或定位预测,而忽略了在迫降飞行过程中,信息条件的缺省以及飞行员操作的人为因素影响。因此在该研究中,综合考虑飞行员、航空器、环境条件等多重因素,并对信息缺省的情况进行分析,对于构建更加精准的搜寻范围划设方法模型具有重要意义。
现依据决策场的相关理论[10-11],对迫降过程中飞行员的应急决策行为进行描述,并结合风场、地形等环境因素构建耦合飞行员应急决策行为的航空器飞行动力学模型。在不稳定因素干扰或信息缺省的情况下,运用MATLAB软件模拟航空器的迫降飞行过程,据此确定搜寻区域的范围和优先级,并与传统方法对比,验证本文方法可靠性。
1 航空器迫降飞行建模分析
航空器在飞行途中由于引擎故障等原因导致完全失去动力,此类事故发生时如无法即时恢复动力,航空器操纵困难往往会造成失事。考虑到保有部分动力的航空器失事可能性较低,因此针对航空器失事迫降飞行过程中完全无动力的情况进行建模研究。
1.1 环境因素分析与建模
与航空器迫降飞行相关的环境因素包括风场、地形、特殊天气区域,各因素对航空器飞行的影响方式不同,因此需要逐一分析[12-13]。
(1)风场建模:航空器迫降飞行区域的风速和风向会影响航空器飞行的受力和真实速度,对风场的建模分为初始条件和变化规律两部分。
对于初始条件,以平均风向的出现频率做12个风向段的风玫瑰图,确定出现频率最高的风向段和对应风速作为初始风向和风速。
对于风场的变化规律,可以分为常值风和动态风,在某一区域风场中的风速相对于航空器的速度是缓慢的,因此可以忽略风速风向变化,将动态风视为常值风。考虑到常值风在垂直方向上的分量变化可忽略,且由于风速水平剖面可以更加直观地表示风速随着海拔高度的变化而变化的情况,因此可以通过常值风在水平方向上的变化情况来描述风场。
采用指数分布模型来对不同海拔高度对应的风速进行计算,风在水平剖面的变化情况描述为
(1)
式(1)中:VH为当海拔高度为H时的平均水平风速大小;VS为海拔高度HS处的平均水平风速大小;m为不同地面性质对应的粗糙度系数。
(2)危险地形建模:航空器迫降飞行会出现山峰等危险地形或能见度过低等特殊天气情况,需要飞行员操作航空器躲避相应危险区域从而导致航迹改变,因此对迫降飞行航迹的模拟预测必须考虑山峰、低能见度区域对失事航空器飞行航迹的影响。
对山峰的仿真首先使用山峰模型进行描述,即
(2)
式(2)中:h0为山峰的基准地形高度;hi为第i座山峰的高度;(xsi,ysi)为第i座山峰的轮廓系数;(xOi,yOi)为第i座山峰投影到平面的中心坐标。
飞行员为了确保航空器能够安全迫降,在操纵航空器飞行的过程中,往往会保证航空器与周围障碍物保持一定的安全距离,因此本文将山峰障碍物描述为一个可以完全把山峰包括在内的外接立方体,具体表达式为
Mm={(x,y,z)|Xmmin≤x≤Xmmax,Ymmin≤
y≤Ymmax}, 0≤Hm
(3)
式(3)中:Xmmin、Xmmax为山峰投影到平面上x轴方向的最小、最大值;Ymmin、Ymmax为山峰投影到平面上y轴方向的最小、最大值;Hm为山峰的海拔高度。
(3)低能见度区域建模:在三维空间中,可以认为低能见度的区域其正上方的所有区域均不能飞行,这里可以把低能见度区域及其上方区域视为障碍物,在三维空间中能见度的障碍物模型表示为
Mv={(x,y,z)|Xvmin≤x≤Xvmax,Yvmin≤
y≤Yvmax},z≥Hv
(4)
式(4)中:Xvmin、Xvmax为低能见度区域投影到平面上x轴方向的最小、最大值;Yvmin、Yvmax为低能见度区域投影到平面上y轴方向的最小、最大值;Hv为低能见度区域最低高度。
1.2 航空器迫降飞行受力分析
航空器迫降飞行过程中受力[14-15]主要包括
(5)
式(5)中:L为升力;D为阻力;Y为侧力;Cl为升力系数;Cd为阻力系数;Cy为侧力系数;V0为航空器飞行的相对速度;S为机翼面积;ρ为空气密度。
根据气体状态方程式,空气密度与海拔高度的关系为
(6)
式(6)中:ρH为海拔高度H的空气密度;ρ0为标准状态下的空气密度;αT为空气温度梯度;T0为绝对温度。
1.3 迫降航空器的姿态调整
在完全无动力的航空器飞行过程中,遇到低能见度区域、山峰障碍物,飞行员为躲避障碍物则会调整尾翼为飞机施加横向力以转向,从而导致航空器航向与风向夹角改变。基于以上分析建立航空器运动模型。
(1)航空器航向与风向在同一条直线上,有
(7)
式(7)中:X为航空器失去动力迫降的水平位移;θ为航空器俯仰角;t为迫降飞行时间;g为重力加速度;M为航空器重量。
(2)航空器航向与风向不在同一条直线上,有
(8)
式(8)中:X为航空器失去动力迫降的水平位移;Y为航空器失去动力迫降的纵向位移;β为航空器偏航角。
2 飞行员应急行为决策模型分析
2.1 飞行员行为分析
飞行员通过机载探测设备及目视观察等方式收集信息并采取决策对航空器姿态、速度等进行调整。而随着迫降飞行时间的推移和航空器自身情况的改变,飞行员的心理状态、对完成任务的期望和个人决策方式等都会发生变化,过程中不同的决策选择对整个迫降飞行过程发挥不同的推动作用,从而影响航空器最终的迫降位置点[16]。
根据上述分析得出飞行员在迫降过程中至少需要在以下几个阶段针对不同状况根据相关信息进行决策。
(1)迫降飞行初始阶段,在当前航线是否有适合迫降的场地,以此调整飞机航向。
(2)迫降飞行过程中,基于雷达等探测设备(或目视)提供的信息判断,安全范围内是否存在山体,以此调整飞机航向(或高度层)。
(3)迫降飞行过程中,基于雷达等探测设备(或目视)提供的信息判断,安全范围内是否存在低能见度区域,以此调整飞机航向(或高度层)。
这些是和否的决策,最终结果如何则是在结合外界数据,由通过飞行员内心对各个结果的偏好强度在一定的阈值设定规则下得出的结果。飞行员的决策框架如图1所示。
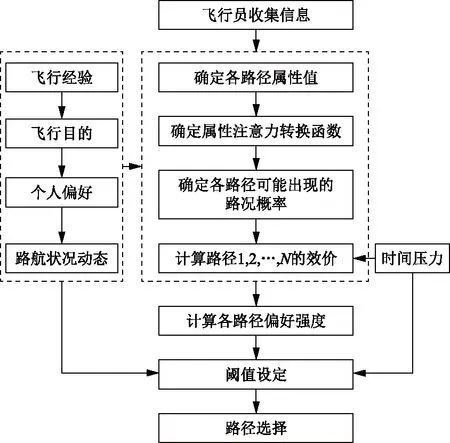
图1 决策框架Fig.1 Decision framework
2.2 模型建立
决策模型的体系结构主要包含3个要素:可选择的路径、相应路径的状况和相应路径的属性。飞行员需要决策的情况主要包括迫降飞行初始阶段选择迫降场地,飞行过程中遇到危险地形(不稳定天气区域)时选择如何改变方向。
对于初始阶段的迫降场地选择,假设对于各路径而言可能的路径状况为目视条件良好或恶劣。通过发放问卷进行数据统计的方法,得出在无诱导信息的条件下,飞行员选择迫降飞行路线的准则中主要考虑3个属性:时间(T)、位移(D)、危险区域数量(I),并且用随机误差项表示其他属性对路径选择的影响。
(1)建立属性矩阵M。备选路径在各种自然状态下所有属性的评价用属性矩阵表示。设定在迫降飞行过程中,飞行员可选路径为路径1和路径2,两条路径均存在恶劣和良好两种路径状况。
路径状态矩阵如表1所示。
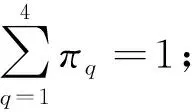

表2 属性矩阵表Table 2 The attribute matrix
(2)建立权重矩阵W(t)。W(t)为在t时刻的权重向量,根据决策场模型的假设,在迫降飞行的过程中,随着时间的推移权重向量会平稳随机地发生变化,权重向量为
(9)
(3)建立比较矩阵C。n为可选路径的数量,此处可选路径为2,因此比较矩阵表现形式为

(10)
(4)随机误差项E(t)。假设该项服从μ=0,σ=0.2的正态分布。
(5)确定效价向量V(t)。效价向量的每一个分量Vi(t){i=1,2,…,n}当其为正时表示对备选路径i接近,为负时则表示回避,V(t)由4个部分组成
V(t)=CMW(t)+E(t)
(11)
在计算飞行员的路径偏好强度时,为将其转化为规范化决策矩阵,引入标准化计算公式
(12)
(6)确定反馈矩阵S。反馈矩阵为特征值小于1的对称矩阵,即该矩阵主对角线上的元素相等,这样的设定即保证了系统较强的稳定性也保证了模型的记忆能力和反馈效应在每一个决策结果可选项都是相同的。
(7)飞行员动态应急行为决策模型P(t)。
P(t+h)=SP(t)+V(t+h)
(13)
式(13)中:P(t)为二维偏好强度向量;分量Pi(t)为路径i{i=1,2}在t时刻的偏好强度,用来对该路径偏好强度进行度量。
飞行员对两条路径的初始偏好以P(0)来表示,其值的正负代表不同意义:正值代表喜欢,负值代表厌恶,0代表中立。
时间间隔h为仿真计算步长,即飞行员对不同路径在自然状态πq{q=1,2,3,4}下属性j{j=1,2,3}进行比较到最终产生效价所需要的时间,为了更加贴近实际的偏好变化设定h→0,从而得到飞行员对各条路径的偏好强度以一个近似时间连续的形式发生改变。
(8)路径选择规则。对于路径选择决策时的情景设定往往决定了路径选择的规则。考虑到迫降飞行中应急决策往往会受到时间限制,因此采用时间限制规则,设定停止时间TD决定决策过程的停止,Pm(TD)=max[Pi(TD)],i=1,2,…,n,当时间t=TD时被选择的路径即是偏好强度为Pm(TD)的路径,决策结果产生,决策过程停止。
3 仿真实验设计及模拟
在上文对航空器迫降飞行以及飞行员应急行为决模型研究的基础上,以MATLAB软件作为仿真平台,构建航空器迫降飞行的虚拟场景。假设航空器处于完全无动力状态,使用我国高高原航线常用机型B737-700,以拉萨贡嘎国际机场2011—2016年间的风速风向变化为依据设置风场,参考文献[9]得到设定迎角对应的升力系数、阻力系数及设定偏航角对应的侧力系数,最终得到的动力学参数如表3所示。

表3 动力学参数Table 3 Dynamic parameters
在航空器处于完全无动力迫降状态下,航空器姿态仅可进行小角度左右偏转调整,并根据上文对影响航空器飞行因素的分析,最终设置4条代表性路径。①路径1:航空器初始飞行方向沿Y轴的正方向,不考虑侧风影响;②路径2:航空器初始飞行方向相比于路径1增加Y轴负方向上10°偏航角;③路径3:在航空器初始飞行路径上考虑在飞行途中遇到障碍物并向右偏转进行避让的情况;④路径4:在航空器初始飞行路径上考虑在飞行途中遇到障碍物并向左偏转进行避让的情况。
考虑路径设置情况,参考文献[11]简化比较过程,进行路径1和路径2、路径3和路径4两组比较实验,根据属性比较结果和表1确定的路径状态矩阵,得到两组属性评价如表4和表5所示。

表4 路径1、2属性矩阵表Table 4 The attribute matrix of Path1 and Path2
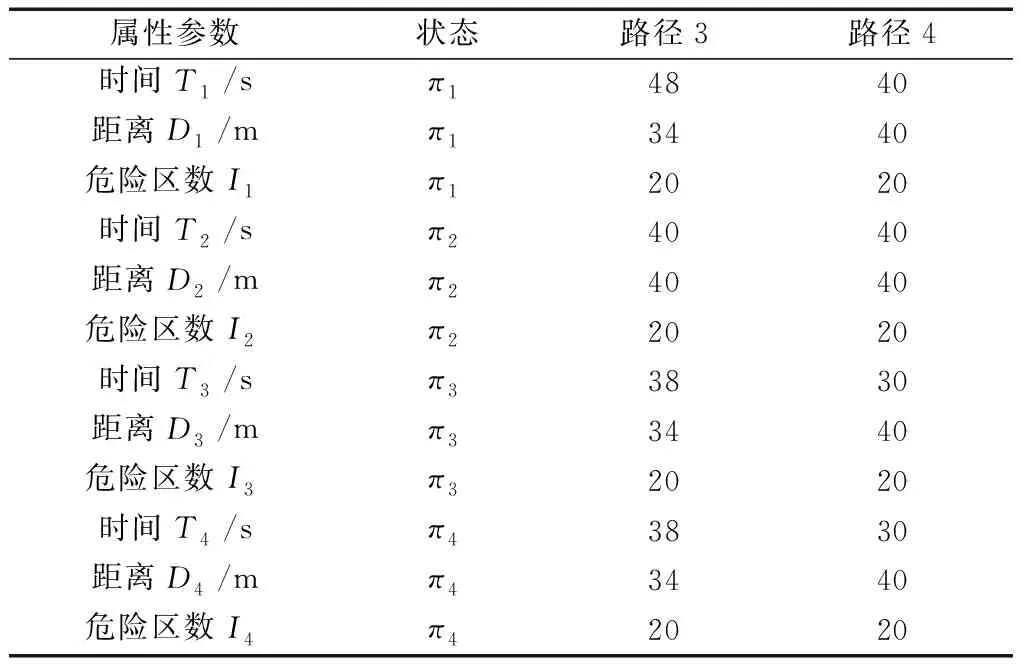
表5 路径3、4属性表Table 5 The attribute table of path 3 and path 4
假设飞行员对两组实验中的任意两条路径均无初始偏好;路径状况可能出现的概率设定为π1=0.1,π2=0.3,π3=0.2,π4=0.4;属性注意力转换
概率取r1=0.5,r2=0.3,r3=0.2;反馈矩阵中的元素取S11=S22=0.95,表示对备选路径前一个时刻的偏好强度有较好的记忆;取S12=S21=-0.03表示备选路径之间的相似程度较低,偏好差异大。最终在MATLAB环境中进行计算结果如图2和图3所示。
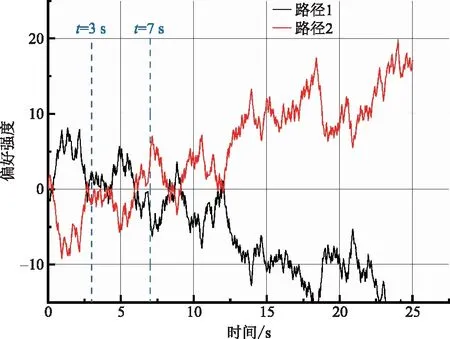
图2 路径1、路径2的偏好强度变化趋势Fig.2 Change trend of preference intensity of path 1 and path 2
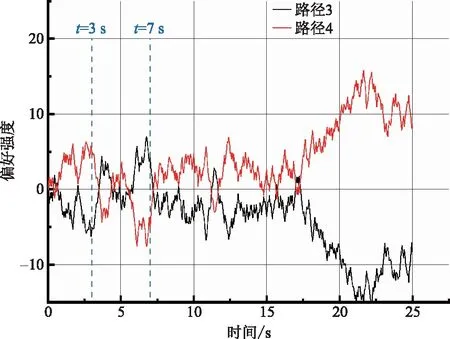
图3 路径3、路径4的偏好强度变化趋势Fig.3 Change trend of preference intensity of path 3 and path 4
对于路径选择,采用时间规则进行结果分析,分别取TD1=3s、TD2=7 s、TD3>7 s,路径偏好强度比较结果如表6所示。
表6中,Pi{i=1,2,3,4} 分别表示飞行员对路径1、路径2、路径3、路径4的偏好强度。为了体现飞行员决策的合理性,在迫降过程中不轻易改变决策倾向,因此选取TD3>7 s时的偏好强度作为比较结果。4条路径最终迫降地点如图4所示。

表6 偏好强度比较结果Table 6 Comparison results of preference intensity
参考文献[9]可知,目前关于航空器搜寻标准规定的第一搜寻区域为以点(0,0)起沿航向方向相对X轴对称,边长为18.5 km的正方形区域;现有研究常用方法确定的第一搜寻区域,为以点(6 462,0)位置起沿航向方向相对X轴对称,边长为11.2 km的正方形区域。
考虑到以上区域数据确定且范围较大,为突出本文模型结果对以上规范化区域仅用于结果比较而不在图4中展示。
根据图4所示的迫降地点坐标,与上述两个区域进行比较结果显示,模型确定了航空器可能迫降位置的优先级排序且均满足在第一搜寻区域内。综上,本文模型具有可行性。

图4 结果可行性验证Fig.4 Feasibility verification of results
4 实验结果分析
前文对航空器迫降飞行全部信息条件已知情况下进行的实验模拟,可以得到确定的迫降地点且均位于第一搜寻区域内。在此基础上,对航空器受到不稳定干扰因素影响或在部分信息条件缺省时的搜寻区域的范围和优先级进行进一步研究。
4.1 不稳定因素情况下的搜寻范围划设
4.1.1 考虑侧风影响
根据初始路径特点,选择初始条件中未考虑侧风影响的路径1,进一步研究航空器的飞行轨迹以及搜寻区域的范围和优先级。基于路径1的初始航线设置侧风,为保证侧风对航空器侧向偏移影响达到最大,设置侧风风向为垂直于航空器初始航向,同时飞行员不考虑进行航向回调。
4.1.2 考虑危险地形影响
根据初始路径特点,选择初始条件中未考虑危险地形影响的路径1做进一步研究。
基于路径1的初始航线设置危险地形,允许航空器进行左右转向操作。为将航空器受地形影响扩大至最大,调整参数使航空器恰好绕过障碍物,之后继续保持该轨迹飞行而不进行航向回调。
根据以上设置,最终分别得到航空器受到侧风、危险地形影响时,航空器发生最大侧向偏移的飞行轨迹如图5所示。

图5 考虑不稳定因素影响的飞行轨迹Fig.5 Flight trajectory under the influence of unstable factors
在此基础上,根据前文确定的各条路径的优先级,在航空器迫降飞行初始条件信息已知,且受不稳定干扰因素影响的情况下,确定的航空器搜寻区域的范围和优先级如表7所示。
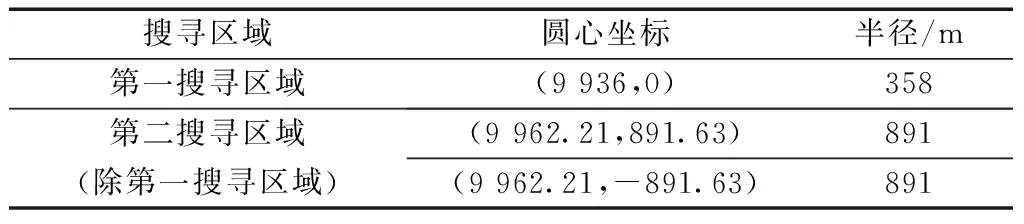
表7 考虑不稳定因素影响的搜寻区域划设Table 7 The search area under the influence of unstable factors
对比上文所述标准规定的第一搜寻区域和现有研究常用方法确定的第一搜寻区域可见,在不稳定因素影响下本文模型划设的搜寻区域满足在第一搜寻区域且精度更高。考虑突出本模型展示效果的原因,此处不进行对比图形展示。
4.2 信息条件缺省情况下的搜寻范围划设
4.2.1 航空器迫降飞行初始高度未知
考虑到航空器迫降飞行初始高度主要影响航空器水平飞行距离以及侧风影响下的航向偏移量,因此在路径1和路径2的初始条件下进一步研究航空器的飞行轨迹以及搜寻区域的范围划设。
已知中型以上的民航飞机巡航高度一般为海拔7 000~12 000 m的高空,因为初始高度未知,设定以Hmax=12 000 m为航空器迫降飞行的初始高度上限,以Hmin=7 000 m为初始高度下限。最终得到航空器飞行路径1和路径2在初始高度未知情况下的飞行轨迹如图6所示。
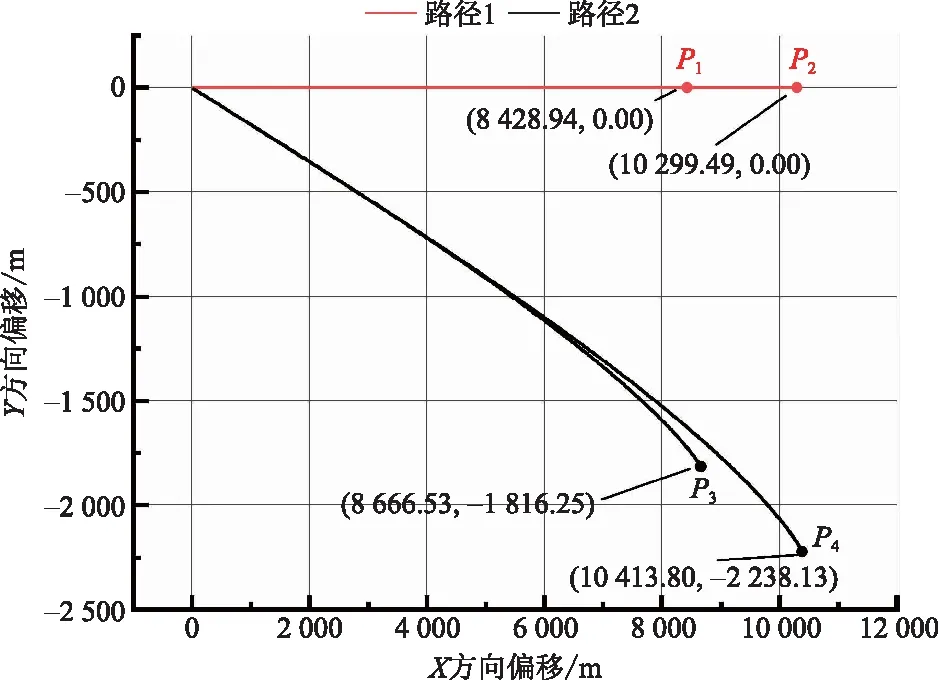
图6 初始高度未知的飞行轨迹Fig.6 Flight trajectory with unknown initial altitude
4.2.2 航空器初始航向未知
仅初始航向未知的情况下,考虑到航空器在正常飞行突发事故的情况下一般不会出现与既定航向偏差超过90°的情况,因此设置未知的初始航向在(-90°,90°)范围内变动。根据前文设置的初始条件,航空器初始高度为H0=10 100 m,航空器受风场影响,最终可能迫降的区域如图7所示。
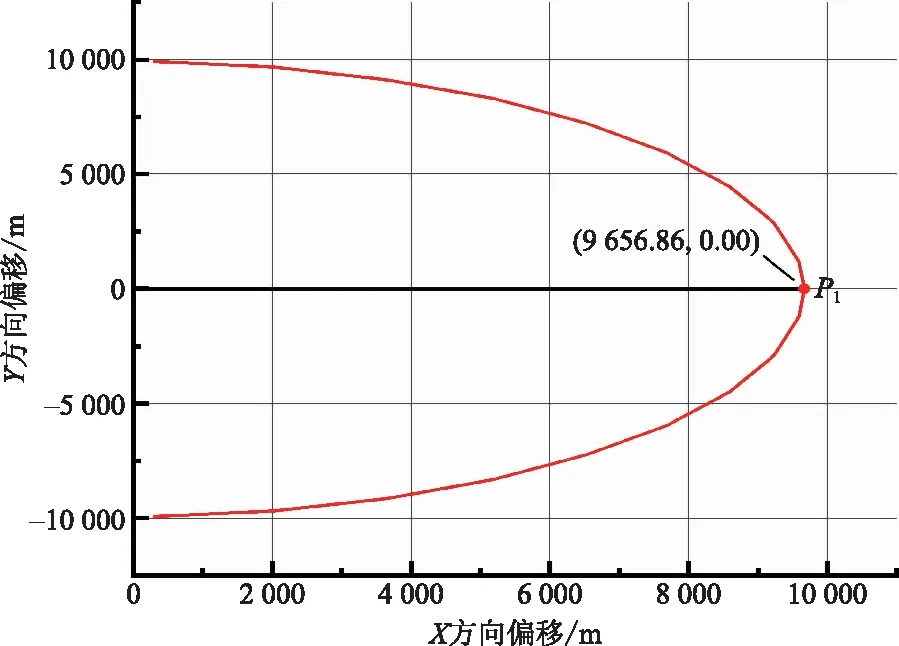
图7 初始航向未知的航空器迫降区域边界Fig.7 Crash area boundary with unknown initial heading
在此基础上,根据前文确定的各条路径优先级,确定出部分迫降飞行条件信息未知时,航空器搜寻区域的范围和优先级如表8所示。

表8 考虑部分飞行条件未知影响的搜寻区域划设Table 8 The search area under the deficiency of conditions
对于初始航向、高度均未知的情况,将上述仿真模型初始高度分别设置为航空器飞行最大/最小可能高度即12 000 m和7 000 m,形成两条曲线所围成的不规则区域即为可能的迫降区域。该区域包含在第三搜寻区域内,此处不进行重复展示。
对比可见,在信息条件缺省情况下本文模型划设的搜寻区域均在传统方法和标准规定的第一搜寻区域内且精度更高。考虑突出本模型展示效果的原因,此处不进行对比图形展示。
5 结论
经分析研究,得出如下结论。
(1)构建一种失事航空器搜寻区域划设的方法模型:该模型综合考虑了飞行员应急行为决策、航空器飞行动力学以及环境因素的影响。
(2)通过实验仿真,证实了模型的可行性。
(3)通过实验结果分析,验证了模型在航空器受到不稳定干扰因素影响或缺省信息条件的情况下,划设的搜寻区域较于单纯依靠动力学模型的方法精确度更高。

