初始泥浆对吹填土抗液化强度CRR的影响

张巍巍， 袁延召， 王彦军， 李小龙， 王攀， 费召阳

(1.中国冶金地质总局青岛地质勘查院， 青岛 266100; 2.中国海洋大学环境科学与工程学院， 青岛 266100)

由于海洋港口城市在兴建过程中，土地资源日益紧张，因此吹填土工程应运而生，吹填土工程虽然能够有效解决土地问题，但是工程所用的材料多为海底或疏浚的泥沙等材料，其材料经过吹填作用形成了具有一定承载力的土体结构，中间分布着若干较厚的由于吹填工艺或吹填的材料不同而形成的富水软土土层[1]，这些地层由于孔隙水含量较大，土骨架以及孔隙中存在颗粒较小的粉土颗粒[2-3]，而大量研究，发现细粉颗粒含量FC(粒径小于0.075 mm的颗粒质量比)对于土体在地震作用下的抗液化性能影响较为显著，且细粒中的黏粒的存在对于地震作用下的抗液化能力影响较为显著，如在CRR不变的前提下，FC>35时，混合料CRR值随着FC的增大而降低，且土体的相对密度Dr=60%时，CRR随着FC的增加而降低[4-6]。并且根据土样的液化以后的不排水抗剪强度测试，发现其液化后强度随着FC的增加而先降低后增强，并且在FC=20%时地层的CRR和抗剪强度最低[2-3, 7-9]，并且从吹填土工程的研究[10]中发现，吹填材料中存在大量的黏土颗粒，而在沉积过程中发生分选沉积，且细颗粒与粗颗粒的沉积速度并不相同，因而导致沉积后的随着地层深度的FC逐步降低[11-12]，且针对沉积后的地层进行液化程度分析可知细粒土含量对于后期土层受动载作用下的抗液化强度CRR等有重要影响[13]。

因此吹填土初始泥浆(原浆)的FC对于吹填土地层形成后的CRR的影响较为重要，但是对于初始泥浆的FC与后期地层的CRR关系的理论研究较少，因此，现探讨初始泥浆的FC对吹填土地层地震作用下的抗液化强度CRR的影响机制以及规律，为判断吹填地层抗液化指标以及配置初始泥浆配比等工作提供理论指导。

1 基于FC含量状态的吹填土CRR值理论研究

吹填土的地层由人工吹填自然沉积，其沉积的过程相对于大陆地层形成，存在周期短，可塑性强，欠固结程度高等特点[2]，因此，经研究发现FC对于土层的液化指数CRR较为明显，其中根据颗粒接触状态的概念提出，土层的力学特性是由土层中不同粒径颗粒的接触状态多决定[6, 8]。

1.1 土颗粒接触状态理论

细粒含量FC对于土体力学性质的影响较为显著，为了描述FC对粗细颗粒混合料力学特性的影响，因此前人提出了颗粒接触状态，将土体视为不同粒径的粗细混合料组成，其接触的形式形成了土体的力学特性，一般将土体根据接触形式[14](图1)分为，FC =0视为粗颗粒直接接触状态；0≤FC≤FCth位粗颗粒直接接触，细颗粒逐渐填充其孔隙，FCth

图1 吹填土颗粒接触状态Fig.1 Contact state of filling particles

(1)

式(1)中：ec为纯砂粒土的孔隙比；ef为纯粉粒土孔隙比。

1.2 骨架孔隙比理论

在颗粒接触状态的理论中，土骨架之间的孔隙是否由细颗粒填满作为骨架接触状态的判定，因此本文利用骨架空隙比ek定量分析不同粒径的颗粒骨料的接触状态[2]，而ek为土颗粒中骨架颗粒的孔隙体积与土骨架体积之比，对于粗粒土组成的混合料骨架时的理论公式为

(2)

而对于粗细颗粒混合料中细粒参与土骨架构建时，有

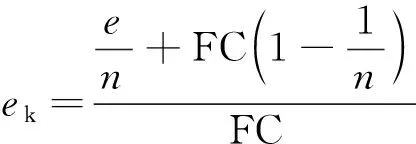
(3)

式中：e为土体的孔隙与土颗粒之比;n=Gc/Gf，其中Gc为粗粒土相对密度，Gf为细粒土的相对密度;θ为土体内摩擦角，由于土颗粒相对密度为2.6～2.7,因此n取值为1。因此将式(2)和式(3)简化为

(4)

1.3 基于FC含量状态的CRR理论

一般认为，土体的CRR的值随着e的增大而降低，但是通过近期的研究发现e不能完全体现CRR与土体的关系[5]，特别是当FC<25%以及FC>35%时土层呈现类粗粒土或类细粒土的状态时，e不能充分反映细粒参与土骨架后的土体的结构发生的变化，因此，采用ek能够更合理地描述混合料的CRR的情况，经过大量的实验验证与理论，统一将基于不同颗粒接触状态的粗细颗粒混合土层CRR的表达为

(5)

因此，将式(1)和式(4)代入式(5)得

(6)

2 吹填土初始泥浆对沉积后地层FC影响规律研究

在吹填土地层的形成实际上是人工模拟天然土层的形成过程，由于吹填土原浆在水中沉积过程，受到的应力环境的变化不断地进行颗粒分选与凝结，因此在吹填土沉积过程中其浆体成分组成与沉降速度同时变化[1, 15]，因此以吹填土的浆体形态作为研究对象，将吹填土的沉积过程简化为土颗粒的分选与土骨架的成分构成作为沉积模型研究要点，其中颗粒沉积随着分选逐渐由单颗粒沉降到颗粒流沉降再到土体固结形成地层。

2.1 吹填土颗粒沉降规律研究

针对吹填土颗粒沉积过程中吹填土原浆中砂粒以及粉粒的粒径不同，球形颗粒在静置的流体中，颗粒密度大于流体密度，先分析颗粒的沉积所受的重力Fg、浮力Fb以及阻力Fd3种作用力(图2)，最终得到自然沉降规律模型为

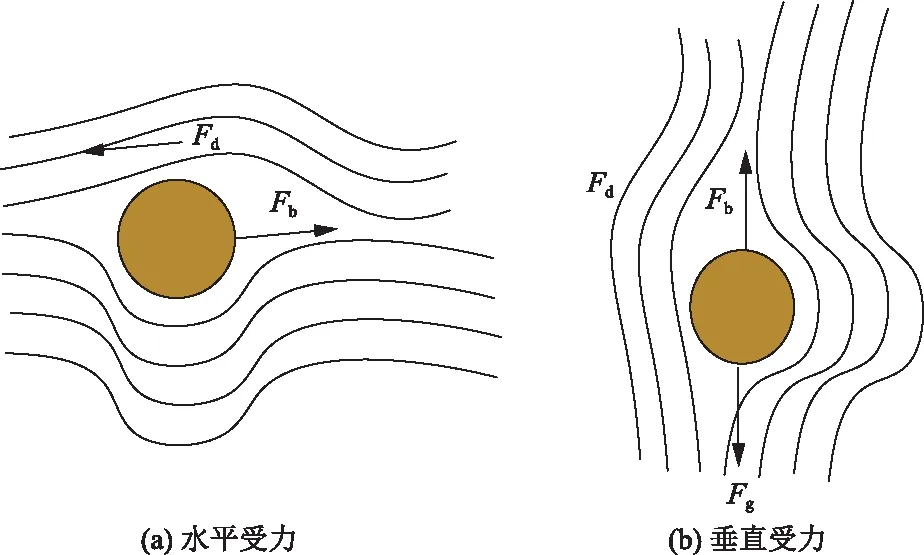
图2 吹填土颗粒受力分析Fig.2 Force analysis of filling soil particles

(7)

式(7)中：ρ为流体密度，kg/m3；ρs为颗粒密度，kg/m3；D为颗粒的当量直径，m；ut为颗粒与流体的相对速度，m/s；Cd为阻力系数，是雷诺数Re的函数，由试验确定。

由牛顿第二定律可知，在土颗粒的沉积过程中

三力的合力公式为

Fg-Fb-Fd=ma

(8)

式中：m为颗粒质量；a为水流造成的土颗粒加速度值。

虽然在水中沉积的过程中其颗粒分为加速沉积、迅速沉积以及减速沉积3个过程[16]，由于对于较细颗粒而言，其沉积过程中，可视为匀速沉积为主，因此设置ut设为自重沉积速度。

(9)

整理后得到其自重沉积速度为

(10)

2.2 吹填土颗粒分选规律研究

因为细颗粒粉砂在沉降过程中，颗粒受到自重应力以及水平紊流的作用下其沉降的流速ω，对于不同粒径的土颗粒产生不同的沉降速度，因此，根据水阻力以及颗粒的粒径建立相对运动关系，因此根据颗粒在紊流作用下的拟离心运动进行受力分析可知

(11)

式(11)中：F为水流冲刷力；x为颗粒沿水流方向的单位距离；v为颗粒流速。

设置颗粒之间的粘滞系数为μ，并依据stock公式[17]，在颗粒未达到终速之前，可以作用在颗粒上的力设置为

(12)

式(12)中：t为颗粒迁移单位距离x用的单位时间。

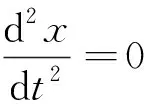
(13)

(14)

颗粒受重力的沉降过程则是由式(10)变形可得颗粒的迁移速度为

(15)

由式(14)与式(15)得

(16)

由式(14)变形可得

(17)

积分可得

(18)

(19)

式中：x1为最小扰动力状态下的迁移距离；x2为最大扰动力状态下迁移距离。

而沉降过程中，根据动量守恒原理

Ft=mut-0

(20)

(21)

(22)

式中：T为水流波浪的一个扰动周期。

由式(19)可得

(23)

则针对不同的粒径进行分析，细粉砂：

(24)

粉土颗粒：

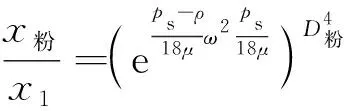
(25)

因此吹填土原浆沉积后地层的FC为式(25)与式(24)的比值，也即

(26)

3 吹填土原浆-沉积分层CRR模型

根据相关研究发现，泥浆浑浊液随着水流下沉，沉降速率ω随着深度变化的关系为

(27)

式(27)中：ω为泥沙沉速；d为泥平均粒径；γs为泥沙比重；γ为水的比重；g为重力加速度；μ为水的黏滞系数；h为沉降深度。因此结合式(6)、式(26)和式(27)可得其不同层位的地层的粉细砂的自然分选后的泥沙级配的理论公式为

(28)

4 吹填土原浆-沉积分层CRR模型验证分析

考虑到自然沉积过程中吹填土地层的级配受到颗粒粒径以及沉降深度，造成沉积后的地层的不同级配，因此在对潍坊的某处吹填土场地的沉积后的地勘资料对相关模型参数的两个方面进行了分析，①吹填土颗粒形成不同层位的FC分析；②吹填土地层的抗液化能力情况分析。

4.1 吹填土颗粒形成不同层位的FC分析

针对东海潍坊某地粉细砂材质的吹填土原浆进行室内实验分析，并依据公式法所需的参数，对吹填土初始泥浆相关参数测定如表1和图3所示。

图3 吹填土颗粒级配比例Fig.3 Gradation ratio of dredger fill particles

表1 吹填土原浆基本参数Table 1 Basic parameters of fill pulp

针对潍坊的吹填土，对其黏性颗粒也即颗粒直径小于0.075 mm的黏性颗粒在原浆中的比例进行了取土测定，并对场地进行分层进行标贯实验N75值，测定不同地层的因此对地层的2、4、6、8、10 m的地测进行分析，由吹填土的原浆的测定其细粒土的含量阈值，分析该初始泥浆的FCth。

=0.431 5

(29)

因此首先对各层的FC依据式(26)进行计算，通过计算结果(图4)，在地层深度小于4 m后，细粉颗粒含量小于FCth，并由此可知，细粉颗粒在地下4～5 m位置以上会参与土骨架的构件，且对比勘察值分析，勘察值在0.3～0.5浮动，且勘察值FC10(深度10 m处FC)相对FC2(深度2 m处FC)有一定的提升，可以反映在吹填土沉积过程中，细颗粒具有分选效果，然而计算值的土颗粒分选现象较为明显，FC10大于FC2的值提升范围为0.1～0.9，且在h=6 m处最为接近，这是由于，细粉颗粒含量在6 m左右处出现阈值FCth，其中计算值与勘察值差距最大处出现在2 m处，计算值FC2约为0.9，相对的勘察FC2含量为0.5。

图4 FC勘察值与计算值对比Fig.4 Comparison of FC investigation value and calculated value

4.2 吹填土地层的抗液化能力情况分析

根据勘察单位给出的标准贯入锤击数(N1)60值，如表2所示，依据美国NCEER砂土液化判别公式[式(30)]计算勘察CRR，并与计算值进行对比分析，如图5所示。

表2 潍坊某吹填土勘察地层标贯实验值Table 2 Experimental values of stratum standard penetration in a weifang soil filling survey

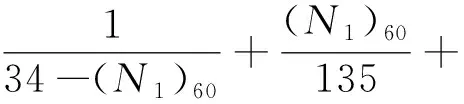
(30)

式(30)中：(N1)60为上覆盖有效压力σ′v=0.1 MPa的修正标准贯入锤击数。

依据式(29)得到CRR勘察值与依据式(28)的计算值(如图5所示)分析可知，其计算值相比勘察值存在偏差，在含粉量FC变小过程中，两者的差距逐渐增大，最大达到0.1左右，但总体的变化规律并不明显，在深度达到6 m时，也即公式法计算的FCth处，两种测定方法，均出现较为缓和的转折点，其中计算值由0.15逐渐变小至0.12，而勘察值也由0.17平滑转变至0.18。且在8 m处，由于FC偏小而出现一定的起伏。造成偏差的原因存在两方面：一方面，随着沉积深度的变化，粗颗粒逐渐占据主导地位，而计算公式方法主要偏于粉粒对于土骨架CRR的影响，因此在FC偏小时，其计算值偏小，另一方面则是由于实际沉积过程中，粗粒土与粉粒土不能像公式法的理想分选状态，存在粗颗粒夹带细颗粒沉积，如图4可知，实际勘察值中，细颗粒分选效果相对于计算值较小，因此，实际沉降地层的级配分选并不明显，这也造成利用标贯实验的N偏大，勘察CRR相对偏大。

图5 CRR勘察值与计算值对比Fig.5 Comparison between CRR investigation value and calculated value

5 结论

(1)基于土力学、分选理论和沉降理论，考虑吹填土原浆中不同粒径颗粒在吹填过程中的自重应力、紊流作用以及离心作用等影响，推导出吹填土原浆FC与吹填后不同层位FC的关联表达式，建立了吹填土原浆FC影响下的不同深度吹填土FC的颗粒分选模型。

(2)依据相关理论公式发现，粉粒吹填土中FC影响土体CRR的影响关系，是与骨架空隙比ek有极大关系，因为土骨架空隙比ek会对土骨架的颗粒构成有更准确的描述，并建立了在FC

(3)根据现场勘查实验对比，并利用CRR的不同计算关系式的计算值对比，计算模型与实测模型变化规律一致，理论偏差较小，能够对吹填土的液化性能指标CRR的判断有一定的理论指导意义。