风电用双列圆锥滚子轴承疲劳寿命数值分析
杨村堃,李 泠,樊恒明,张洪伟,翟佳宇
(北京石油化工学院机械工程学院, 北京 102617)
风力发电机各轴承常年在野外作业,风速、温度及载荷对其都有很大影响,因而对风电轴承有着特殊的要求。风电轴承较高的技术复杂度使其成为风电行业公认的国产化难度最大的两部分(轴承和控制系统)之一[1]。主轴承应用于无主轴、无齿轮箱直驱风力发电装置[2],由于圆锥滚子轴承不仅可以承受较大的径向载荷,而且可以承受轴向载荷,必要时还可以承受较大的力矩载荷[3]。因此,主轴承所使用的轴承类型为双列圆锥滚子轴承。
目前国内外学者对圆锥滚子的接触应力及寿命预测进行了研究。李润林等[4]提出一种基于坐标向量模拟轴承内圈、滚子变形及接触点位置的方法,计算了双列圆锥滚子轴承接触载荷,并以此为基础给出了寿命计算方法。李震等[5]建立了双列圆锥滚子轴承拟静力学特性分析模型,该模型能够快速地分析双列圆锥滚子轴承在复杂工况下的轴承内部载荷分布和疲劳寿命。胡广存等[6]完成了双列圆锥滚子轴承的动力学分析,对轴承的最大接触压力以及疲劳寿命进行了研究。梁勇[7]在对双列调心滚子轴承进行分析时,忽略了保持架,得出主轴轴承的最危险部位为轴承内圈。贾现召等[8]基于DesignLife软件完成了三排圆柱滚子轴承疲劳寿命计算。国外Lundbreg G和Palmgren A[9]提出了轴承寿命理论,即L-P理论,该理论目前仍然被广泛地应用于轴承疲劳寿命计算;Ioannides和Harris[10]对L-P理论进行了修正,形成了I-H理论。Bercea等[11-12]提出了一种利用向量坐标运算来计算双列圆锥滚子轴承刚度和疲劳寿命,并探讨了一种准动态分析方法,充分考虑了离心力和陀螺力矩所产生的影响,能够准确分析复杂受力情况下双列圆锥滚子轴承的受力。上述研究对寿命的计算依然是理论计算,其工作量大,观察不到部件发生疲劳的位置,并且采用整个模型仿真对计算机要求高,不利于仿真。笔者基于滚子-滚道最大接触载荷,采用单个滚子-滚道进行整体轴承的寿命预测分析。针对风电用大型双列圆锥滚子轴承,首先计算了其接触载荷分布、接触应力;利用ANSYS Workbench建立了单个滚子有限元接触模型,并进行了静力学分析;利用nCode对应力疲劳寿命进行了预测。
1 双列圆锥滚子轴承接触载荷计算
1.1 轴承结构主要参数
风电用双列圆锥滚子轴承具有尺寸较大、运转速度低、滚子数量多、刚度大、承载载荷大等特点,其在机组中通过螺栓直接与轮毂相连。
双列圆锥滚子轴承在风电机组中作为主轴承的结构图如图1所示。

图1 风电主轴承结构图Fig.1 Structural diagram of wind power main bearing
双列圆锥滚子轴承结构参数如表1所示。
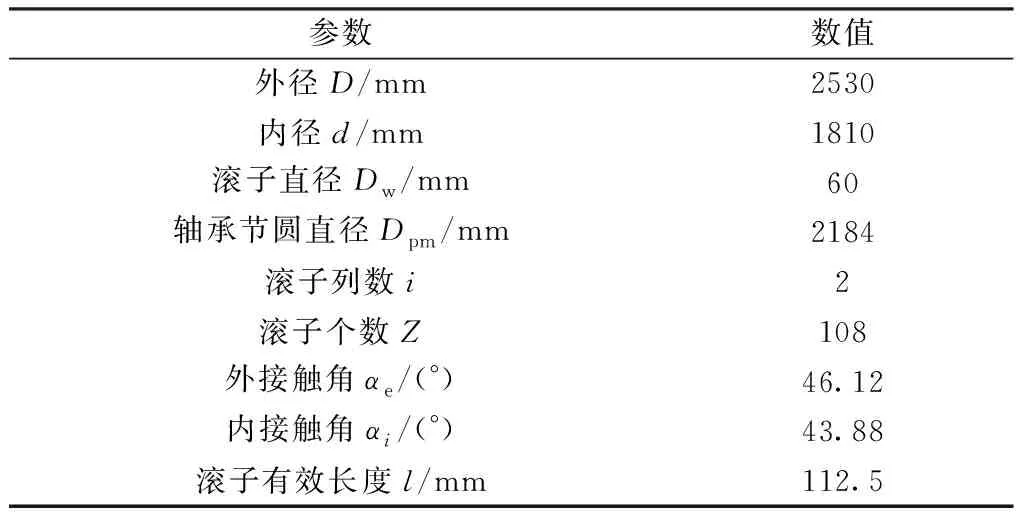
表1 轴承结构参数
1.2 圆锥滚子平衡方程
圆锥滚子的平衡情况如图2所示。设圆锥滚子与内、外滚道和挡边的接触载荷分别为Qi、Qe和Qf,接触角分别为αi、αe和αf。当滚子平衡时,这些载荷必须满足下列平衡方程[13]。

图2 圆锥滚子的平衡Fig.2 Balance of tapered roller

(1)
1.3 静力学平衡方程
双列轴承不必考虑滚子倾斜所产生的附加力矩,在第1列轴承中所产生的不平衡力矩可以由第2列轴承来补偿。其次,双列轴承的刚度比单列轴承大,其转角非常小,由此产生的滚子倾斜力矩也极小,对整体平衡影响不大[13]。双列圆锥滚子轴承整体平衡方程为[13]:

(2)
式中:下标i为对应轴承列数,1表示左列的载荷,2表示右列的载荷;j为每一列对应滚子个数;Fa为轴向载荷;Fr为径向载荷;Mm为倾覆力矩。平衡方程中涉及的载荷和位移方向参考文献[13]。
1.4 接触载荷计算结果
双列圆锥滚子轴承运转过程受径向载荷、轴向载荷、倾覆力矩的作用。计算的载荷数据为企业所提供的设计数据,其中,轴向载荷Fa=270.6 kN、径向载荷Fr=1 210.661 kN、倾覆力矩M=10 229 kN·m。将上述平衡方程基于MATLAB编写程序,采用牛顿迭代进行求解,得到的理论计算接触载荷分布如图3所示。
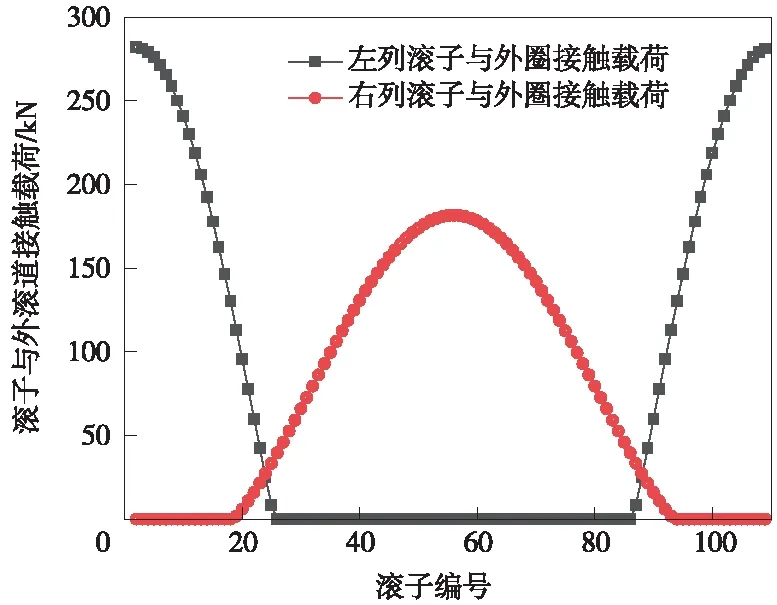
图3 滚子与外滚道接触载荷分布图Fig.3 Distribution of contact load between roller and outer raceway
由图3中可以看出,双列圆锥滚子轴承左列最大接触载荷要大于右列最大接触载荷,左列同时承受载荷的滚子数少于右列同时承受载荷的滚子数。左列接触载荷从∅=0°对应的滚子编号为1的第1个滚子顺时针排列到第108个滚子的接触载荷是先逐个递减直至为零后又逐渐变大;右列滚子载荷的分布情况与左列正好相反。左列接触载荷在∅=0°处第1个滚子与外滚道的最大接触载荷为281.94 kN,除去最大接触载荷后,其他接触载荷呈现出对称分布。接触载荷变化图如图4所示。
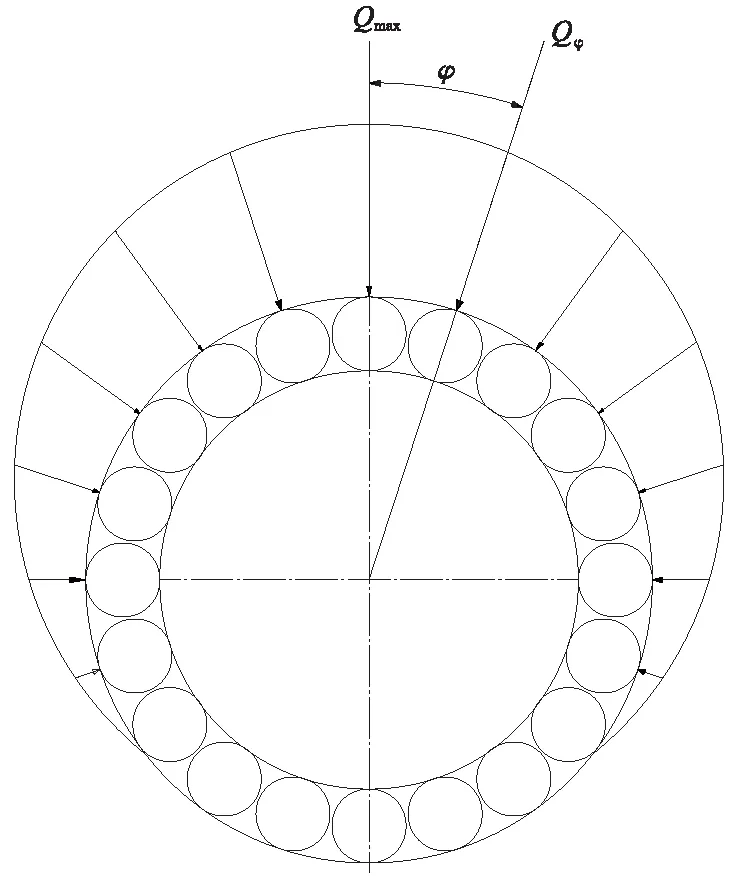
图4 接触载荷变化图Fig.4 Contact load variation diagram
2 接触应力有限元数值分析
2.1 42CrMo材料参数
双列圆锥滚子轴承采用42CrMo材料,其物性参数如表2所示。

表2 42CrMo材料参数
2.2 有限元分析模型
为了简化模型,利用ANSYS Workbench对建立的双列圆锥滚子轴承中承受接触载荷最大的单个滚子-滚道接触模型进行分析。进行网格划分时,采用的单元类型为Solid186单元。为了减少单元数量,在接触区域获得更加准确的计算结果,取内、外圈与滚子接触侧滚道厚度的10 mm进行网格的细化。模型划分完成后的单元数为189 097,节点数为802 285。载荷施加于外滚道,与竖直方向成46.12°。建立的滚子-滚道有限元分析模型如图5所示。

图5 有限元分析模型Fig.5 Finite element analysis model
2.3 结果分析
接触应力分布如图6所示。由图6中可以看出,最大接触应力发生在滚子与内圈滚道接触位置,最大接触应力为1 655.3 MPa,根据文献[14]中的式(24)~式(27)进行最大接触应力理论计算得出的滚子与内圈滚道最大接触应力大于滚子与外圈滚道最大接触应力,最大接触应力为1 754.8 MPa。对比理论最大接触应力与仿真得到的最大接触应力,两者误差为5.7%,说明了模型的正确性。

图6 接触应力分布云图Fig.6 Contour of contact stress
3 疲劳寿命分析
3.1 疲劳寿命理论
对于具有线接触特征的滚子,其寿命计算式为[13]:

(3)
对于双列圆锥滚子轴承,滚道额定动载荷为:
Qc=

(4)
式中:l为滚子有效长度;λ为考虑到滚子端部应力集中和滚子倾斜而引入的降低系数,当滚子受力不均匀时,一般在0.4~0.8之间取值。双算符的上、下符号分别适用于内、外滚道。
内圈当量载荷:
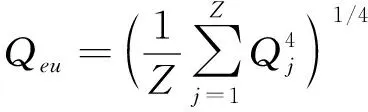
(5)
内圈疲劳寿命:

(6)
外圈当量载荷:
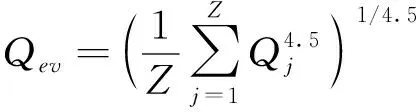
(7)
外圈疲劳寿命:

(8)
轴承修正后的基本额定寿命为:
式中:Qj为第j个滚子接触载荷,根据整体平衡方程计算所得;L10i1、L10i2分别为左列内滚道、右列内滚道寿命;L10e1、L10e2分别为左列外滚道、右列外滚道寿命,bm=1.1。
理论疲劳寿命根据式(3)~式(9)进行计算,其疲劳寿命为3.148×105r。
3.2 疲劳寿命仿真
3.2.1 应力疲劳寿命
进一步利用nCodeDesignLife进行应力疲劳寿命计算。由于风的不确定性,轴承所承受的载荷具有交变性,施加恒定幅值载荷谱来模拟主轴承在运行中受到的交变极限载荷[8],即脉动循环载荷。
根据42CrMo材料参数进行材料S-N曲线的生成,结果如图7所示。
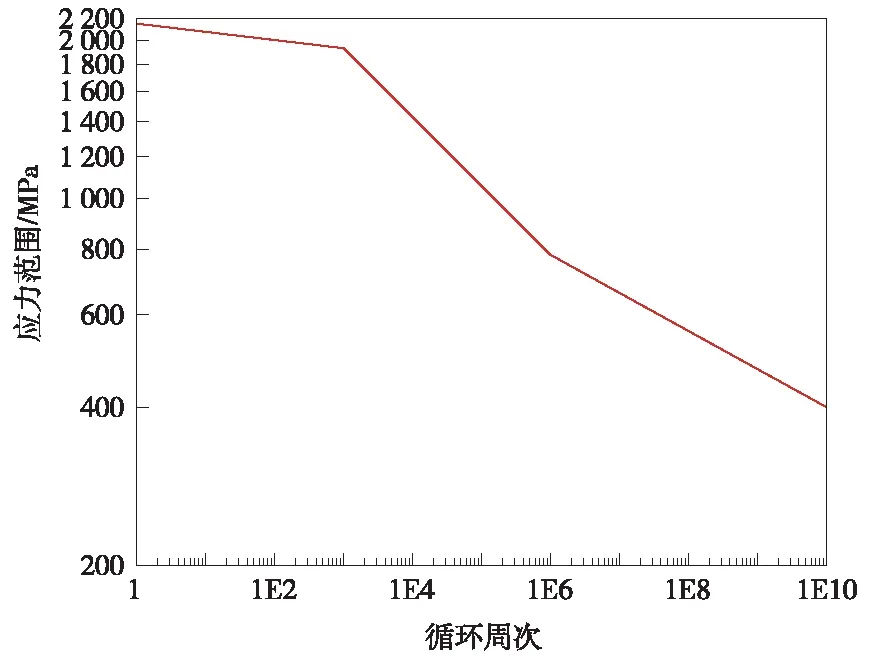
图7 42CrMo的S-N曲线Fig.7 S-N curve of 42CrMo
3.2.2 平均应力修正
软件中S-N曲线平均应力为零,而载荷在统计过程中会存在平均应力不为零时的应力范围或者应力幅,计数得到循环应力幅的平均应力不等于零,故需要对平均应力进行修正。平均应力修正方法有Good-man、Gerber、Interpolate、FKM、Chaboche。笔者选用的应力组合方法是带符号的冯米塞斯应力法(Signed Von Mises),平均应力修正方法为古德曼法(Goodman)。
3.3 结果分析
仿真得到的寿命云图如图8所示。由图8中可以看出,最大损伤位置为滚道与滚子接触位置,疲劳寿命值为3.17×105r。通过对比理论计算与仿真分析的结果发现,理论计算的疲劳寿命与仿真疲劳分析寿命的计算误差为0.69%,说明该仿真方法的可行性。

图8 寿命云图Fig.8 Contour of life
4 结论
(1)针对风电用双列圆锥滚子轴承进行接触载荷、接触应力的理论计算,得出最大接触载荷为281.94 kN。最大接触应力的位置在内滚道上,应力大小为1 754.8 MPa。
(2)建立了单个滚子-滚道有限元分析模型,分析得出的最大接触应力为1 655.3 MPa。与理论计算值对比发现两者的误差为5.7%,最大接触应力发生的位置为滚子与内滚道接触位置,与理论计算得到的最大接触应力值的位置相同,验证了模型的正确性。
(3)基于nCodeDesignLife进行应力疲劳寿命分析,损伤最大位置在滚子与滚道接触位置,寿命值是3.17×105r,与理论计算值3.148×105相比,两者误差为0.69%,说明仿真方法的可行性。通过提取数值并仿真能够清晰地观察出接触应力、疲劳损伤发生的位置,能够及时对设计的产品进行优化,对实验能够起到一定的指导作用。

