基于Geo-Slope软件的某建筑垃圾堆场边坡稳定性研究

亢 永，赵孟孟，霍思雨，王可依，付士根，宋冰雪，吴 壮

(1.北京石油化工学院，北京 102600； 2.中国安全生产科学技术研究院，北京 100020)

随着我国工业化、城市化进程的不断推进，每年有大量污染企业面临拆迁和改建，遗留的工业建筑垃圾堆体对生态环境造成了重大的潜在威胁。建筑垃圾堆体是一种特殊土体，存在边坡稳定性和失稳滑坡的问题[1]。边坡崩塌不仅给建筑物或者运输带来损失，还会威胁到附近生活居民的生命财产安全。建筑垃圾堆体发生滑坡的事故屡屡发生。

Geo-Studio软件是一款广泛应用于岩土边坡的数值模拟软件，该软件中的Slope/W分析模块内置多种滑移面搜索方法、孔隙水压力条件、土体强度本构以及加固组件和荷载工况等，不仅可以进行边坡的稳定性分析，也可以进行边坡失效概率和参数敏感性分析；而软件中的Seep/W模块不仅可以分析饱和与非饱和边坡岩土体的渗流问题，也可以分析边坡岩土体的稳态渗流和瞬态渗流，可以定义渗透各项异性，通过瞬态分析得出不同时刻不同点的孔隙水压力分布状况，其结果可被用于Slope/W模块研究边坡稳定性随时间变化的关系。通过Slope/W和Seep/W 2个模块来模拟计算在一般降雨条件下边坡安全系数的大小[2]。

胡志毅[3]从垃圾堆体的滑坡发生过程及形成机理入手，分析了基底岩体抗剪强度、施工建设、暴雨对滑坡的影响。陈云敏等[4]通过对实际工程的垃圾填埋体的边坡进行稳定性计算，分析了边坡坡角和浸润线对垃圾边坡稳定性的影响。付士根等[5]利用高密度电法对垃圾填埋场渗滤液水位进行探测，验证了渗滤液水位是影响垃圾填埋场堆体稳定性的重要因素。根据查阅文献可得，影响垃圾堆场边坡稳定性的因素有垃圾土的抗剪强度参数、垃圾堆场的几何尺寸(坡高、坡角等)、垃圾土的重力密度及孔隙水应力等[6]。

边坡稳定分析的方法有很多， 王玉平等[7]对常用的边坡稳定性分析方法进行了总结归纳，分析了图解法、极限平衡理论、数值分析方法、复合法等确定性分析方法的发展情况。极限平衡法是边坡稳定性分析中最早出现的确定性分析方法，其中包括普通条分法、毕肖普法(Bishop)、力平衡方法、摩根斯坦-普莱斯法(Mogenstan-Price)等方法。赵由才[8]根据Mohr-Coulomb理论，采用Bishop法对垃圾堆体的安全系数进行计算。Seed[9]采用数值模拟的方法对美国的Kettlemam Hills填埋场进行了安全系数的计算，得出用2D模拟计算的安全系数(1.20～1.25)比3D模拟计算的安全系数(1.08)要稍微偏大一些。关志伟[10]结合边坡稳定性数值分析，运用三维有限元软件对稳定性进行了深入研究。

综上所述，在对堆体滑坡的研究方面国内外学者已经做了大量工作，但现有的研究只是针对整个堆体，对堆体内部各条间推力、受力等考虑较少。笔者以某城市建筑垃圾堆体为研究对象，充分考虑影响垃圾堆体边坡稳定性的、失稳破坏的各种主要因素，利用Geo-Studio软件毕肖普方法对堆体边坡稳定性进行评估，并为其设计支护方案提高其稳定性。

1 城市建筑垃圾堆场滑坡影响因素

影响垃圾堆场滑坡主要因素包括地表水及地下水、基底形态、边坡的形态和垃圾的堆排工艺等，每个影响因素既可以单独作用影响垃圾堆体的稳定性，又能够共同作用加剧垃圾堆体的破坏速度。

1.1 排弃垃圾和基底岩土体性质的影响

排弃垃圾的物理力学性质是指垃圾的组成成份、容重大小、吸水性、渣土的硬度、粘聚力等。对于固体垃圾来说，物理力学性质对垃圾场内部的稳定性有很大的影响。对物理性质比较软弱的固体垃圾而言，因为其吸水性比较好，所以很容易发生变形，从而使整个堆体下沉，进而导致坍塌事故。

基底地层的硬度也是影响建筑垃圾堆场稳定性的重要因素之一。堆体地层形成原因不同，如构成堆体基底的物质、颗粒的大小、胶结物的性质和胶结的程度等这些都会造成基底层结构的差别很大，而且随着其他不确定性因素的影响，基底也会具有不同的物理力学性质，从而影响到整个垃圾堆体的稳定性。

1.2 地表水及地下水的影响

水力充填或人工堆积的尾矿坝、粉砂质边坡等土工构筑物不仅在动荷载下易发生液化流滑，而且在静荷载(如上覆堆载、水位变化)下也极可能发生滑移失稳[11]。

水对土体的性质变化具有很大的影响，包括地表水与地下水两类。垃圾堆体基底会因为水的作用而强度下降，土体内聚力、内摩擦角对基底岩土体的强度有很大影响，他们与土体含水量关系密切，内聚力和内摩擦角与含水量成反比。在施工过程中导致地下水、地表水或降水等进入建筑垃圾中，使得固体垃圾间的凝聚力和摩阻力进一步降低，在重力、地下水以及施工扰动的共同作用下超过整个堆体的极限平衡，导致坍塌事故的发生。

1.3 施工存在问题的影响

垃圾堆场边坡的结构设计是保证垃圾堆体稳定的一个重要方面。如果在垃圾堆场的施工和堆排过程中不能达到设计者所设计的性能标准，就会使得垃圾堆场失稳破坏而导致坍塌。

2 城市建筑垃圾堆场边坡稳定性分析

2.1 常用的稳定性分析方法

近年来边坡稳定性受到越来越多的关注，研究稳定性的理论分析方法层出不穷，其中主要有确定性分析方法和不确定性分析方法两大类[12]。确定性分析方法中主要是定性分析和定量分析，其中定性分析方法主要是运用地质勘查、土地历史分析法、工程地质类比法、图解法等。定量分析方法主要有极限平衡分析法、数值分析法、可靠性分析法等。不确定性方法总体上分为人工神经网络法、灰色系统理论、可靠性分析、模糊数学方法等。常用的极限平衡方法有瑞典条分法[13]、简化毕肖普法[14]、简布法[15]、余推力法、萨尔玛法[Sarma][16]、美国陆军工程师法[The Corps of Engineers]、摩根斯坦-普赖斯法[Mogenstan-Price][17]、分块极限平衡法、斯宾塞法[Spencer][18]等。

2.2 简化毕肖普法(Bishop 法)

Bishop 法不用规定滑动面必须是非常标准的圆弧，只要是近似圆弧均可。计算结果比较准确，因为在计算过程中充分地考虑了土体内部条块间的相互作用力，有严格的分割要求，计算方式采用迭代法，这样就能使所有被分割的条块在计算过程中都处于平衡状态。Bishop条块作用力分析图如图1所示。

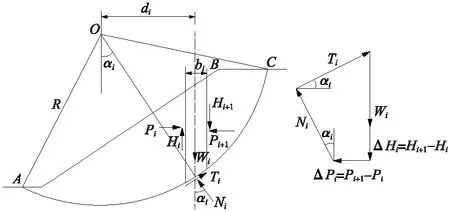
图1 Bishop 条块作用力分析Fig.1 Bishop slice force analysis

从圆弧滑动体中取出某土条i进行分析。如果这个条块处于静力平衡的状态，那么根据垂直方向的力平衡条件可得：

Nicosα=Wi+ΔHi-Tisinα

(1)

当满足安全系数为Fs时，根据此时的极限平衡条件，有：

(2)

式中满足

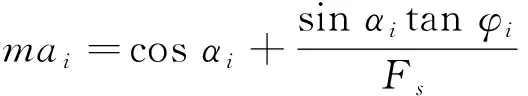
(3)

根据整个滑动土体的力矩平衡条件，每个土条对中心(圆心)力矩的和是零。简化可得：

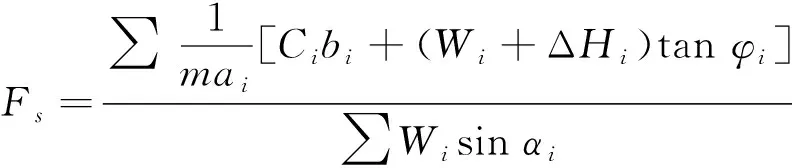
(4)

这就是毕肖普法计算的一般公式，进一步假设Hi=0 ，式(4)可化简为：

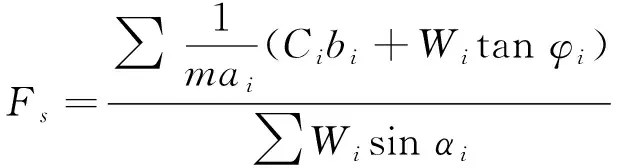
(5)

3 实例分析

3.1 边坡工程概况

以某市一处边坡为模拟对象，其所处地区地貌单元类型为构造剥蚀低丘陵，长期受降雨外力因素的侵蚀和冲刷影响，并且附近500 m建有居民楼。其边坡为台阶型，走向为近南北向，地势南高北低。坡度为63°，坡高为16 m，其中由上到下分别是杂填土2 m、碎石粉质黏土4 m、全风化石英夹板岩4 m、强风化石英岩夹板岩2 m、中风化石英岩夹板岩4 m。根据现场勘测已有的数据建立地质模型，如表1所示。此边坡地质模型面临着滑坡的风险，一旦发生滑坡将对附近居民造成严重的生命财产损失。本次模拟使用Geo-studio软件对比边坡进行建模计算该边坡最小安全系数并确定滑移面的位置，分析其安全性，并提出相应的支护方案增加其稳定性。

表1 某边坡地质模型

3.2 稳定性计算参数选取

结合勘查数据资料，在室内对杂填土和含碎石粉质黏土分别进行土的直接剪切实验，将土制备成几个土样，分别在不同的法向压力(Normal Load)下，沿固定的剪切面给其施加水平剪力(Shear Load)，得其破坏时剪应力即土的抗剪强度。土的抗剪强度是由内摩擦角和黏聚力所组成，可以用库伦公式表示：

黏性土：

τ=σtanμ+C

非黏性土：

τ=σtanμ

式中：τ为土体抗剪强度(kPa)；σ为承受的垂直压力(kPa)；μ为内摩擦角(°)；C为黏聚力(kPa)。

实验得到的数据如图2所示，由库伦公式可知：图中的截距即是黏聚力，斜率就是内摩擦角。由计算可得杂填土的τ和σ关系式可以表示为：τ=σtan 10°+5，所以杂填土的内摩擦角为10°，黏聚力为5 kPa。粉质黏土的τ和σ关系式为：τ=σtan 25°+15，可得粉质黏土的内摩擦角为25°，黏聚力为15 kPa。

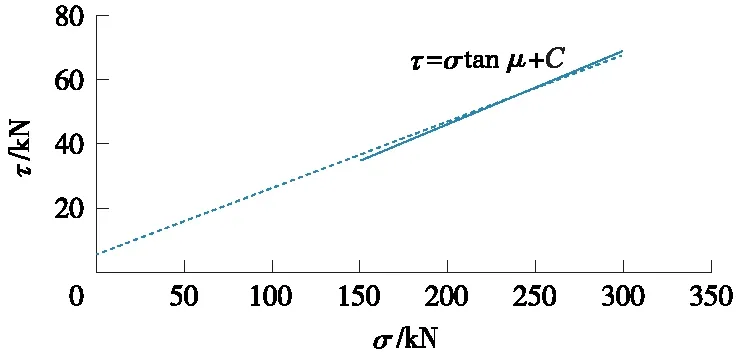
图2 地基土的直接剪切试验数据Fig.2 Direct shear test data of foundation soil

其他3个岩层的物理参数参考王汉勋等[19]的研究。本次滑坡整体计算参数的选取结合土体的特征、室内土直剪试验的结果，并且类比其他边坡工程参数取值，最终提出模拟的计算模型材料参数如表2所示。

表2 计算模型材料参数表

3.3 水文地质状况

地形、地质构造和水文、气象等因素综合控制了地下水的分布，同时在垃圾堆排方式的影响下，裂隙逐渐发育为地下水的赋存提供了空间。垃圾堆厂区的雨季集中在6～8月。每逢雨季地下水位会抬高，枯水期则地下水位会下降，由于该区域年降水量小且蒸发量大，因此，地下水位每年的变化幅度不是很大。地下水位年变化幅度为1.25～3.53 m。依据高密度电法探测采集的数据，通过反演计算得到了该垃圾场的浸润线高度，浸润线高度分别离地面7.24～10.5 m。

3.4 Geo-Studio建模

考虑地下水的影响，用Geo-Studio软件进行模拟计算[20]，Geo-Studio软件是一套专业、高效而且功能强大的仿真分析、设计软件，适用于岩土工程和岩土环境模拟计算，包含SLOPE/W、SEEP/W、SIGMA/W等多个模块。其中SLOPE/W是以极限平衡法为计算原理，专门用来进行边坡稳定分析，能够以最简单的操作方法和最快的速度来得到最准确的最小安全系数Fs，而且在很大程度上改进了极限平衡法在分析边坡稳定性过程中的不足。即运用Geo-Studio软件中的Slope计算模块，采用Bishop法计算该边坡最小安全系数和确定滑移面的位置。

3.4.1 最危险滑动面的确定

基于Geo-studio软件结合上述相关的指标值对其进行建模，最终得到无水压力下和自然降雨状态下2种工程的滑坡稳定性示意图，如图3、图4所示。从GEO-SLOPE/W程序中的可视图形化界面中可以看到最危险滑动面、对应的滑动中心位置和相应的稳定系数，滑裂面呈圆弧状沿边坡向横向发展。

图3 无水压力条件下边坡稳定的最小安全系数Fig.3 Minimum safety factor of slope stability under anhydrous pressure

图4 降雨状态下边坡稳定的最小安全系数Fig.4 Minimum safety factor of slope stability under rainfall condition

3.5 稳定性评价

本建筑垃圾堆体边坡的坡高H为16 m，垃圾堆体边坡工程安全等级如表3所示，垃圾堆体边坡抗滑稳定最小安全系数如表4所示。

表3 垃圾堆体边坡工程安全等级

由表3可知，该工程安全等级为三级。根据生活垃圾卫生填埋场岩土工程技术规范CJJ 176—2012，由表4可知，该工程在正常运用条件下的边坡安全系数需要达到1.25[21-22]，而在无水压力状态下的边坡测得的最小安全系数为1.546，故边坡属于安全状态。在降雨条件下最小安全系数为0.775，根据《建筑边坡工程设计规范》远远小于既定的标准安全系数，所以初步断定在降雨工况下该边坡处于不稳定的状态。

表4 垃圾堆体边坡抗滑稳定最小安全系数

4 支护方案设计与实施

4.1 支护方案的选择

边坡支护方案一般分为生物防护和工程支护两大类[23]。生物防护也即生态防护，根据边坡土质条件可分为土质生态边坡防护和岩质边坡生态防护。工程支护的主要结构形式有重力式挡墙、扶壁式挡墙、格构式锚杆挡墙支护、锚喷支护等。

首先，由于边坡支护模拟中，生物防护不是此次所要考虑的优化方案对象，故先予以排除。其次，由之前建立的降雨工况下模型可知，所研究的边坡高为16 m，重力式与悬臂式挡土墙均不适用。考虑到滑坡位置的特殊性，此处不宜采用挡土墙。由于实验模拟过程与现实的差异性，因此，先考虑选用锚杆支护。考虑到土钉支护与锚杆支护的相似性且土钉支护更容易操作，因此，选择土钉支护方案。

4.2 Geo-studio模拟土钉支护

在具体工程中，土钉支护较为普遍，在边坡支护中应用广泛。工程支护中常见的土钉如图5所示。

利用Geo-studio2007分析软件进行实际模拟过程。以土钉数为模拟过程中的实验变量，其他保持不变。得到的优化后的边坡结果如图6所示。

图5 工程支护中常见的土钉Fig.5 Common soil nail in engineering support

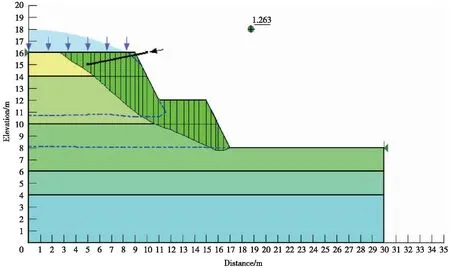
图6 土钉支护下的暴雨工况安全系数计算结果图Fig.6 The calculation result of safety coefficient under the condition of soil nailing

在所设定的参数下，当土钉数量为1根时，坡面达到稳定状态，安全系数较之前大幅提高，达到1.263(大于标准值1.25)。为了研究加固桩数量增加对安全系数的影响，选择继续增加土钉数目。土钉支护数目对安全系数的影响如表5所示，此时的安全系数变化量级小于0.1，说明土钉数目增加对于安全系数影响程度下降且不明显；同时，随着土钉数量的增加，滑移面逐渐向岩层深处移动。

表5 土钉支护模拟分析统计表

5 结论

(1)通过对垃圾堆场危险源进行辨识，采用常用的危险辨识方法来辨识一些基本的风险，进而对建筑垃圾堆的稳定性有较大影响的因素进行了分析，得出结论为基地形态、堆排工艺、堆体边坡形态、地表水、地下水为影响其稳定性的重要因素。

(2)在室内对土质进行直接剪切实验，结合土体的特征和室内试验的结果，及类比其他工程参数值之间的综合考虑，最终提出了抗剪强度参数计算值。

(3)安全模拟实验中，对边坡进行了稳定性分析。当处于无水压力条件下时，边坡处于稳定状态，安全系数大于标准值(1.25);当边坡处于暴雨工况条件下时，对其进行稳定性分析，结果没有达到该有的稳态，安全系数为0.775。

(4)选定了土钉支护方案，在所设定的参数下，当数量为1根时，坡面就可以达到稳定状态，安全系数较之前大幅提高。

(5)模拟计算过程中，所建立的模型是处于理想状态；在实际工程中，边坡各个土层之间的分界并不像所建模型那样清晰。

(2)在模拟计算过程中，只考虑了水压力条件的不同而设计的无水压和降雨2个工况。而现实生活中还有许多其他外在因素影响着边坡的稳定性，如地震等因素，与实际工程问题难免具有一定的差异性。