Einstein-de Sitter时空上具有非线性记忆项的半线性阻尼波动方程解的爆破

欧阳柏平

(广州华商学院数据科学学院,广东 广州 511300)

1.引言

本文研究下面Einstein-de Sitter时空上具有非线性记忆项的半线性阻尼波动方程柯西问题解的爆破,

波动方程解的爆破研究是偏微分方程的一个重要内容.近年来,有关Einstein-de Sitter时空上波动方程的研究吸引了一些学者的兴趣.[1-5]

广义Einstein-de Sitter时空中具有幂次非线性项的单因子波动方程如下所示

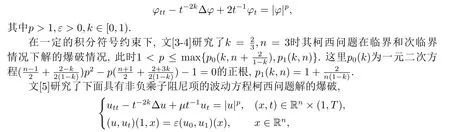
其中p ＞1,ε ＞0,k∈[0,1),μ为非负实数.

运用泛函分析方法和迭代技术,在初始条件满足一定的条件下,作者得到了在临界和次临界情况下解的爆破.

式(1.1)中,如果k=μ=0,则方程化为utt-Δu=Nγ,p(u).

文[6]对上式进行了研究,应用迭代技巧得到了次临界和临界情况下解的爆破.

本文在文[5]的基础上进一步研究带有非线性记忆项的半线性阻尼波动方程解的爆破问题.其目标主要是研究非线性记忆项对其柯西问题解的爆破影响.另外,从式(1.1)等式右边的积分项可知,其对系统的影响是非局部的.另一方面,由于(t-s)-γ是衰减的,这表明最近的信息对系统的作用越大.

一般的二阶波动方程研究思路主要是运用Kato引理.然而,对于含有阻尼项和非线性记忆项的波动方程如问题(1.1),应用Kato引理有不少困难.基于此,本文采用有关文献提出的迭代技巧[7-13]对问题(1.1)进行研究.其难点在于如何引入合适的能量泛函得到其迭代框架和第一下界,从而进行迭代,证明其解的全局非存在性以及生命跨度的上界估计.此外,与文[7-13]中不同地方还表现在需要恰当处理由于阻尼项引起的时间空间积分.

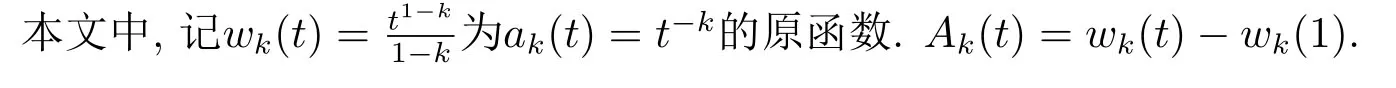
2.主要结果

下面先给出(1.1)的柯西问题能量解的定义.

定义1设(u0,u1)∈H1(Rn)×L2(Rn).u是问题(1.1) 在[1,T) 上的能量解,如果

3.定理的证明

首先讨论下面方程的正解

式(3.19)式提供了问题(1.1)的迭代框架.接下来将寻找其第一下界.

由Φ(t,x)定义以及其为式(3.1)的解,结合式(2.2)可得