Long-time Behavior of Solution for the Non-autonomous Extensible Suspension Bridge Equation with Memory and Time Delay

WANG Suping(王素萍) ,MA Qiaozhen(马巧珍)

(1.School of Mathematics and Statistics,LongDong University,Qingyang 745000,China;2.School of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,China)

Abstract:Long-time dynamics of the solutions for the suspension bridge equations without delay effects have been investigated by many authors,but there are few works on extensible suspension bridge with memory and time delay.In this paper,we consider the long-time behavior for the non-autonomous extensible suspension bridge equation with memory and time delay.Existence of pullback attractor is shown by using the contractive function methods.

Key words:Extensible suspension bridge equation;Delay;Memory;Pullback attractor;Contractive function

1.Introduction

Physical reasons,non-instant transmission phenomena,memory processes,and specially biological motivations like species’ growth or incubating time on disease models among many others,make delay differential equation become an important field of applied mathematics.[1-4]In the field of mathematics,we mainly pay attention to the well-posedness and asymptotic behavior of delay differential equation.On the asymptotic behavior of delay differential equation,there are many results.[5-9]In [7-9],the authors investigated the models in which the forcing term contains some hereditary features.These situations may appear,for instance,when we want to control the system by applying a force which takes into account not only the present state of the system but also the history of the solutions.No doubt at all,the asymptotic behavior of dynamical systems with delay is an interesting and challenging problem,since it can provide useful information on the future evolution of the system.

Therefore,in this paper,we consider the following extensible suspension bridge when the forcing term contains some hereditary characteristic:

The model (1.1) describes the vibration of the road bed in the vertical direction,whereu(x,t)denotes the deflection in the downward direction;ν∂turepresents the viscous damping,andα,νare positive constants.The real constantprepresents the axial force acting at the ends of the road bed of the bridge in the reference configuration,namely,pis negative when the bridge is stretched,positive when it compressed.The convolution term means that the stress at any instanttdepends on the whole history of strains which the material has undergone and produces a weak damping mechanism.ku+denotes the restoring force,k ＞0 denotes the spring constant,the functionu+(x,t)=max{u(x,t),0}.τis the initial time.φis the initial datum,h ＞0 is the length of the delay effects,and for eacht∈[τ,T],we denote byutthe function defined on [-h,0] withut(θ)=u(t+θ),θ∈[-h,0].

It is well known that Lazer and McKenna in [10] presented the following suspension bridge equation

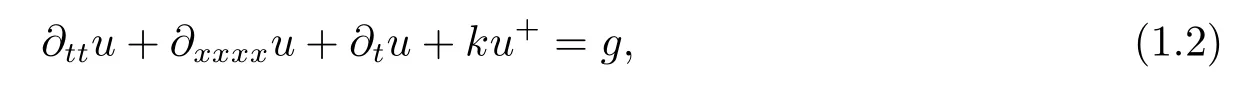
as a new problem in the field of nonlinear analysis.Adding a nonlinear forcef(u)to the model(1.2),it becomes

ZHONG,et al.[11]have investigated the existence of strong solutions and global attractors for (1.3).Similar models have been studied by several authors.[12-16]For example,MA,et al.proved the existence of global attractors in [12] as well as pullback attractors in [13]for the coupled suspension bridge equation.In [14],MA,et al.showed the existence of uniform compact attractors for the coupled suspension bridge.Bochicchio,et al.[15]studied the existence of global attractor for the extensible suspension bridge equation and obtained a regularity result of attractor.The existence of global attractors for the suspension bridge with linear memory was achieved by Kang in [16].

However,none of the above conclusions contain time delay.With respect to the suspension bridge equations with time delay,see [5-8] and references therein.Park in [5] considered the following suspension bridge with time delay

and obtained the existence of the finite dimensional global attractors under the condition of 0＜|a1| ＜a0.The authors in [6] studied the following nonlinear plate modelling nonautonomous suspension bridge with time delay inΩ=(0,π)×(-l,l)

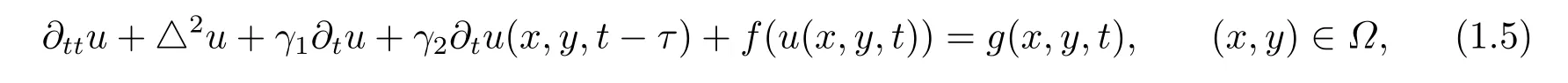
and proved the existence of uniform attractors.In [7],the authors also studied the following non-autonomous suspension bridge with variable delay

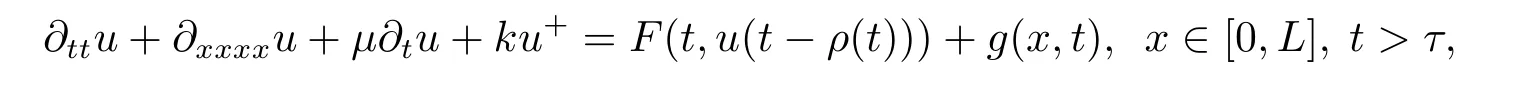
and proved the existence of strong pullback attractors by using the theory of attractors for multivalued dynamical systems.Recently,we considered the following suspension bridge when the delay termF(t,ut) is driven by a function with very weak assumptions

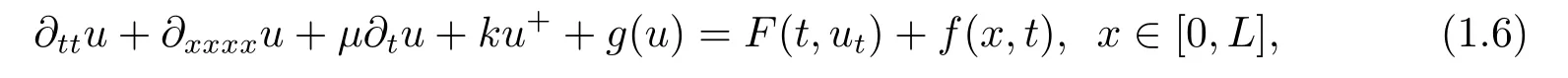
and proved the existence of pullback attractors in [8].

For other partial differential equations with time dependent delay,see [9] for details.But,as far as we know,there is no results about extensible suspension bridge equations with memory and time delay.Our main result states that the dynamical system (1.1) possesses pullback attractor by using contractive function.

Source termF(t,ut) containing some hereditary characteristic,we assume that it is defined asF:R×CL2(Ω)→L2(Ω) and satisfies the following conditions:

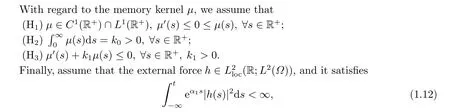
whereα1＞0 will be determined later.

The rest of this article consists of three Sections.In the next Section,we define some functions setting and iterate some useful lemma and abstracts.In Section 3,we prove wellposedness and pullbackD-absorbing set.In Section 4,we firstly show pullbackD-asymptotically compact and then prove the existence of pullbackD-attractor for (1.1).

2.Preliminaries

In this section,we iterate some notations and abstract results.

Firstly,we defineD(A)={u∈V,Au∈H:u(0,t)=u(L,t)=∂xxu(0,t)=∂xxu(L,t)=0},whereA=Δ2=∂xxxx,thenA:D(A)→His a strictly positive self-adjoint operator.For anys∈R,the scale of Hilbert spaces generated the powers ofAis introduced as follows:

In particular,we denote as|Au|the norm ofD(A).It is obvious thatV4⊂V ⊂H=H* ⊂V *,hereH*,V *are the dual space ofH,Vrespectively,and each space is dense in the following one and the injections are continuous.

In the following,we iterate some useful lemmas and abstract results.

3.Pullback Absorbing Set in CH

In this section,we will construct the process associated to problem (1.1),then prove the existence of pullback absorbing set inCH,and in the sequelC,Ci(i=0,1,2,···) denotes arbitrary positive constants,which may be different from line to line and even in the same line.

4.Pullback Attractors in CH