Fokas-Olver-Rosenau-Qiao方程的Cauchy问题

宋瑞丽 ,王书彬 ,苏晓

(1.郑州经贸学院公共教学部,河南 郑州 451191;2.郑州大学数学与统计学院,河南 郑州 450001;3.河南工业大学理学院,河南 郑州 450001)

1.引言

研究下列Fokas-Olver-Rosenau-Qiao(FORQ)方程的Cauchy问题:

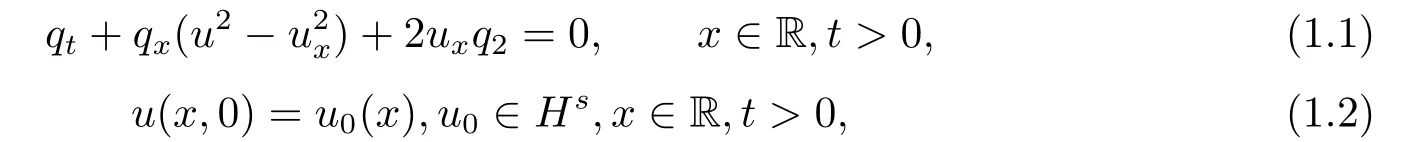
其中q=u-uxx.下标x,t表示分别关于x,t求偏导.

1854年Russell[1]对孤立水波进行了探讨,这推进了人们对浅水波方程的研究.1895年,Korteweg和de Vries在对浅水波运动进行研究时提出KdV方程

并证明方程(1.3)有光滑孤立波解.[2]1981年,Fokas和Fuchssteiner研究广义KdV方程的可积性和双Hamilton结构时推导出如下方程

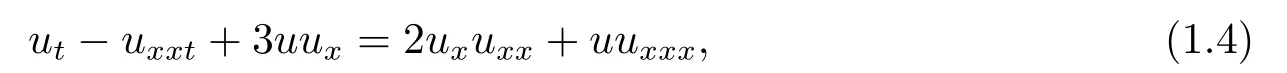
并研究了它的孤立子结构和守恒律.[3]Camassa和Holm从Euler方程在浅水波条件下的Hamilton量渐进展开中得到

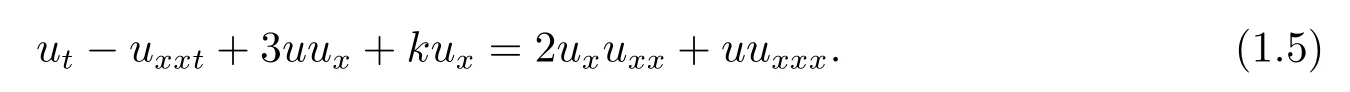
此方程被广泛的命名为Camassa-Holm(CH)方程.这里u(x,t)表示流体在t时刻x点的流速,k是常数并与波速有关.Camassa和Holm证明了CH方程具有双Hamilton结构、完全可积性并且给出(1.4)在k=0时的孤立波解.[4-5]Cooper和Shepard用变分法不仅给出(1.5)在k=0时的精确孤立波解,而且给出(1.5)在k=0时的最优变分解.[6]CH方程具备丰富的物理背景和多种数学特性,成为浅水波理论新的主流方程,许多数学和物理工作者都对它进行了研究,并取得了丰硕的成果.[7-9]

Novikov在众多CH方程的成果上,提出了具有三阶非线性项的方程(Novikov方程)[10]

Hone,Lundmark和Geng发现Novikov方程具有完全可积性、双Hamilton结构及尖波孤立解.[11-12]学者也对Novikov方程的Cauchy问题强解的局部存在性、唯一性以及解的爆破进行了研究.[13-15]

Fokas,Olver,Rosenau和QIAO在研究可积系统时提出了一类具有三阶非线性项的方程,就是Fokas-Olver-Rosenau-Qiao(FORQ)方程.[16-18]Olver,QIAO和Rosenau先后研究了FORQ方程的双Hamilton结构以及尖波解.[17-19]QU和LIU研究了FORQ方程的孤立子的稳定性.[20]FU,GUI,LIU 和Olver证明了修正的CH方程在Besov空间是局部适定性的,描述了解的爆破机理,确定解在有限时间内发生爆破并给出最大存在时间的下界,并证明了行波解的不存在性.[21-22]

2.预备知识

FORQ方程的双哈密顿结构可以用下面的方程描述：

这是研究它在Sobolev空间中的适定性最简便的形式.为简便起见,改写FORQ方程(1.1)为如下的非局部形式:

3.主要结论及证明