基于组合赋权法的小波阈值降噪综合评价指标研究

熊春宝，庞红星

基于组合赋权法的小波阈值降噪综合评价指标研究

熊春宝，庞红星

(天津大学建筑工程学院，天津 300072)

均方根误差、信噪比、相关系数、平滑度等传统小波降噪效果评价指标适用于纯净信号已知的情况，而在实际应用中监测所得信号的纯净状态一般是未知的．为解决传统评价指标的局限性问题，提出一种基于组合赋权法的综合评价指标．该指标首先是在理论分析和实例验证的基础上，从增减性与物理意义角度确定了指标分量为均方根误差和平滑度；然后利用阈值极大法对两个指标进行归一化；最后采用熵权法与变异系数法对均方根误差和平滑度的归一化值进行相应的权重计算并线性组合相加．综合评价指标的极小值对应的分解尺度与小波基函数即为最优小波参数．通过对3种不同信噪比(5dB、12.5dB、20dB)的仿真信号进行分析，结果表明，该综合指标均成功识别到最优的分解尺度和小波基函数，降噪效果达到最佳．与其他综合指标相比，该指标的准确性和普适性更好．另外，将该指标应用到GNSS监测信号中也是可行的，具有一定的工程价值．

小波阈值降噪；综合评价指标；熵权法；变异系数法；组合赋权

随着多系统、高采样率以及可以实时动态差分的全球导航卫星系统(global navigation satellite system，GNSS)的快速发展，其在大型土木工程结构的高精度健康监测领域中得到广泛应用[1-3]．然而，环境激励下所获得的GNSS监测数据会不可避免地遭受噪声污染，进而影响后续分析．因此，借助滤波算法对其进行降噪是预处理中很重要的一环．小波降噪技术因具有优良的局部时频分析能力和多尺度特性在动态变形监测信号降噪中备受青睐[4]，但小波降噪效果受分解尺度、小波基函数等参数影响．因此，如何准确选取并确定所需参数对小波降噪质量的提高具有重要的研究意义．

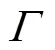
针对以上研究的不足，本文提出一种新的综合评价指标用于小波阈值降噪质量的评估．该综合指标利用熵权法和变异系数法对均方根误差和平滑度的归一化值进行组合赋权，通过综合评价指标的极小值来识别小波降噪参数的最优值．

1 小波阈值降噪及常用降噪评价指标

1.1 小波阈值降噪原理

一般地，非平稳、非线性的原始含噪信号经小波变换后，分解得到相应的近似系数和细节系数，通过设置合适的阈值对细节系数进行量化处理，最后重构得降噪信号．小波阈值降噪[12-13]的具体步骤主要分为以下3步．

步骤1 信号分解．确定分解尺度和小波基函数，对原始含噪信号进行小波分解．

步骤2 阈值量化．选取合理的阈值准则和阈值函数，并对步骤1获得的细节系数进行量化处理．

步骤3 小波重构．利用小波逆变换对步骤2处理后的细节系数和未处理的近似系数进行重构，获得降噪信号．

上述小波阈值降噪过程中，影响降噪效果的主要因素包括分解尺度、小波基函数、阈值准则以及阈值量化函数．对于一般的动态变形监测信号，前两个因素的最优值对降噪效果的影响大于后两者的选取，并且软阈值或硬阈值函数已满足大部分信号的降噪要求[14-15]．因此，选取最佳的分解尺度和小波基函数将对小波阈值降噪质量的提高具有重要作用．

1.2 常用降噪评价指标

目前，常用的小波阈值降噪效果评价指标主要有信噪比SNR、均方根误差RMSE、平滑度、相关系数等[16-18]．其中，信噪比定义为原始信号与噪声信号的能量比值，SNR值越大代表降噪效果越好．均方根误差是指原始信号与降噪后信号方差的平方根，RMSE值越小代表降噪效果越好．平滑度为降噪后信号的差分值平方与原始信号差分值平方的比值，反映的是降噪后信号局部突变的程度，值越小代表降噪效果越好．相关系数是指降噪后信号与原始信号的相似程度，值越大表示两者相似度越高，降噪效果越好．

虽然上述常用评价指标从不同的物理含义角度评估降噪效果，但单项使用时具有一定的局限性和片面性．由于实际监测所得信号的原始纯净信号是未知的，利用单项指标进行评判时可能会发生无极值现象，致使难以确定所需参数(分解尺度、小波基函数)的最优值．有时甚至可能会出现极端情况，例如当原始含噪信号中噪声部分仅滤掉很少一部分或者没有被去除时，SNR值就会达到很大，RMSE值会很小或为零，值也几乎等于1，这些结果均可能导致研究人员对滤波算法的降噪效果产生错误的判断．

为进一步说明单项指标在原始纯净信号未知情况下应用的弊端，以单项指标确定最优分解尺度为例，利用小波阈值降噪方法对标准测试信号“Blocks+ Heavysine”的叠加进行不同分解尺度的降噪效果分析，其中添加5dB的高斯白噪声．4个指标随分解尺度的变化趋势如图1所示．从图1中可以发现，SNR随分解尺度增大而逐渐减小，即呈负相关；RMSE呈正相关；随分解尺度增加而骤降并逐渐收敛平稳；呈负相关．4个指标在整个变化过程中均无极值出现，因此无法确定最优的分解尺度．由于不同小波基函数具有类似规律，鉴于篇幅未列出，下文如未特殊说明均以分解尺度为例．通过上述分析可以看出，寻找一种既能保留单项指标优点又可以克服上述弊端的评价指标显得尤为重要．

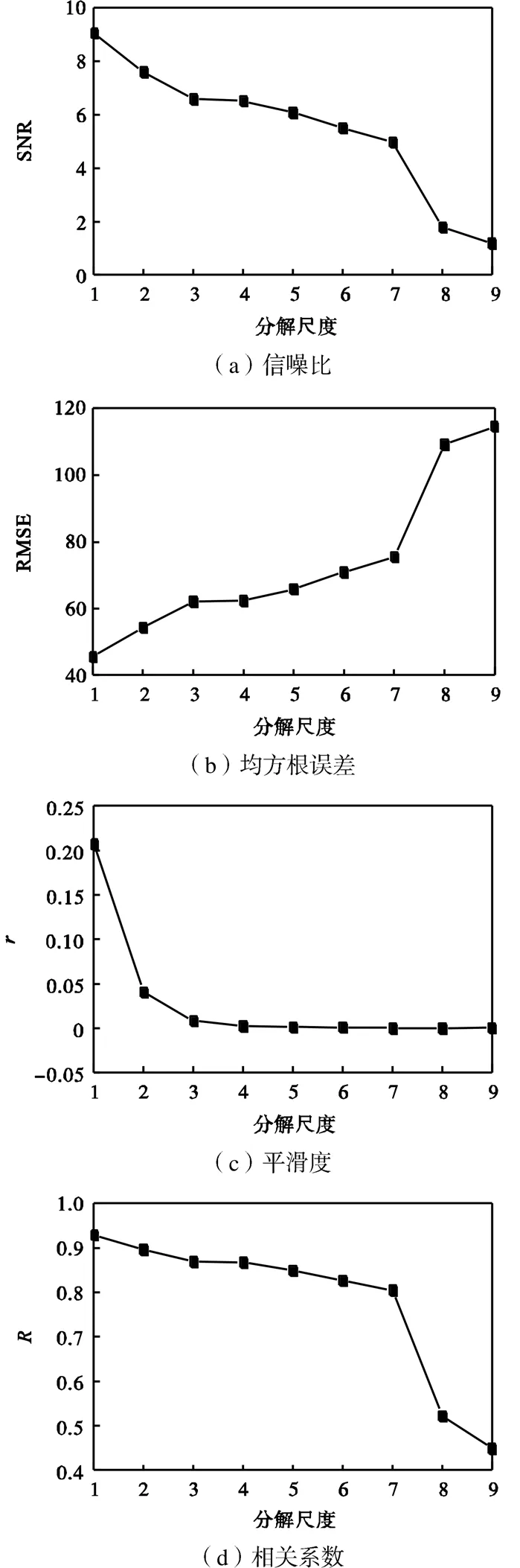
图1 分解尺度对单项评价指标的影响

2 综合评价指标

为解决上述问题，本文构建一个新的综合评价指标．该指标的构建过程主要分为两步：①单项评价指标选取；②综合评价指标体系确定．接下来将在第2.1节和2.2节分别进行阐述．

2.1 单项评价指标选取

本文所提综合评价指标的核心思想是当指标达到极小值时所对应的分解尺度或小波基函数即为该参数的最优值．

综合评价指标的组成分量选取准则如下所述．

(1) 增减性．从第1.2节分析可知，SNR、、与分解尺度呈负相关，仅有RMSE呈正相关，理论上为使综合指标出现极值需选RMSE．

(2) 物理意义．表示降噪前后信号的相似性，即两信号的偏差；由SNR公式看出其分子为RMSE的平方，两者均与RMSE物理含义具有一定重叠．4个指标中仅有反映降噪信号的局部突变特性．

综上分析，选取RMSE和作为综合评价指标的组成分量．

2.2 综合评价指标体系确定

单项组成指标确定后，面临如何将两个指标揉合成一个指标的问题，即多指标向单指标的转换．笔者借鉴综合评价方法，将两指标分别进行赋权并相加得本文综合评价指标．由于两指标融合过程中存在单位、数量级的差异，首先需要将指标进行无量纲化处理，本文采用阈值极大化法将它们归一化到[0，1]之间．两指标计算及归一化公式如下．

均方根误差RMSE：

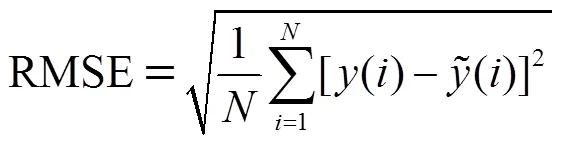
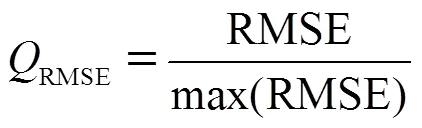
平滑度：

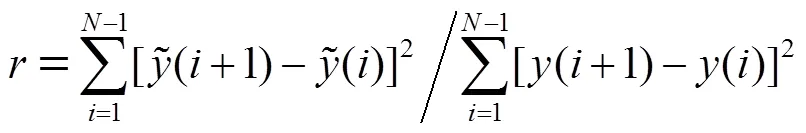
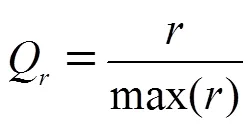
然后，对归一化指标进行权重系数计算．本文选择由熵权和变异系数组合赋权的方法，弥补了单一赋权法的缺陷，使各指标的权重系数更加科学与合理．

熵权法[19]权重计算具体步骤如下．

步骤1 计算两个指标的比重．

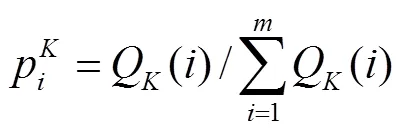
步骤2 计算两个指标的熵值．

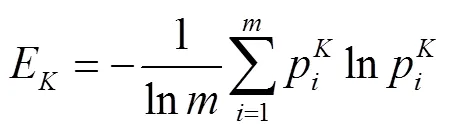
步骤3 计算两个指标的权重．

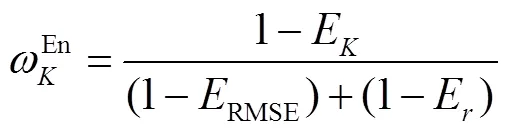
指标熵值越小，则熵权权重越大，说明该指标重要性越大；反之，重要性越小．

变异系数法[20]权重计算公式如下：

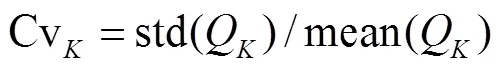
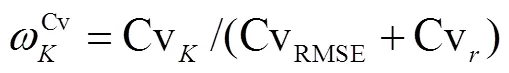
变异系数越大，则权重越大，越说明该指标可以反映评价差异．

组合赋权的常用处理方法有乘法组合赋权和加法平均组合赋权等[21]．由于乘法组合赋权对数据要求较高，如单一赋权法权重值不能为零或负值，以及要求各单一赋权法之间具有强相关性，局限性较大；而加法平均组合赋权对数据要求较少，权重值可为正、负或零，并且能够将权重值或评价比重较大的指标突显出来．经过综合考虑，本文选择加法平均组合赋权计算本文综合评价指标OPT，具体见式(10)和(11)．

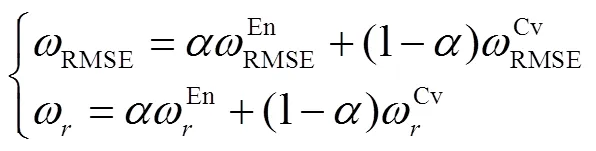
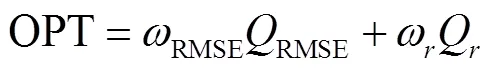
3 仿真分析

为保证本文所提综合评价指标的工程适用性，需先证明其正确性和普适性．考虑到工程监测信号的纯净信号具有未知特性，因此利用仿真信号进行验证．为确保仿真信号可以尽可能与实际监测信号相一致，选择3个不同频率的正弦信号、线性信号以及噪声信号叠加而成的信号进行分析，仿真信号的时域变化如图2所示．其中采样数为2000，采样频率为2Hz．仿真信号公式如下：

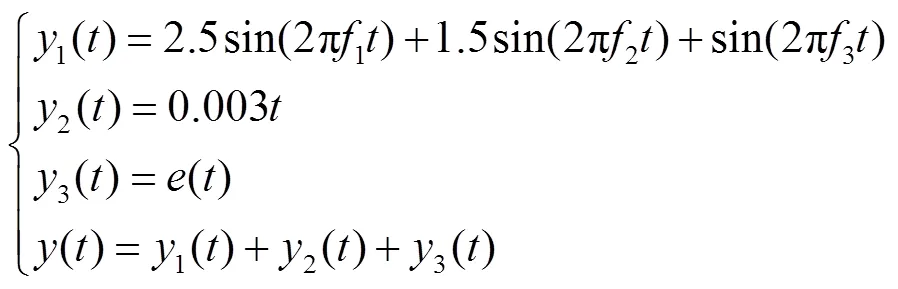
正确性和普适性的证明方法如下．

(1)验证正确性．首先基于纯净信号已知条件，计算不同分解尺度和小波基函数的单项指标，寻找出正确的最优值；然后基于含噪信号(即纯净信号未知)情况，计算本文所提综合评价指标并识别极小值，通过与纯净信号已知时所得最优值进行对比，观察其是否一致．

(2)验证普适性．如果考虑所有含噪情况，计算量将难以想象，再者也不切实际．因此，为避免结果偶然性同时结合工程监测数据的含噪特点，本文选择具有代表性的3种信噪比(5dB、12.5dB、20dB)进行研究，然后比对不同信噪比情况下纯净信号已知与未知时的综合评价指标对应参数的最优值和纯净信号已知时的单项指标参数的最优值．

3.1 纯净信号已知

首先计算纯净信号已知条件下的单项指标来确定正确的最优层数．依据单一变量原则，除分解尺度外，其余参数保持不变．其中为防止分解尺度过大导致信号失真严重，层数选择1～9层；小波基函数暂选“db8”，阈值估计方法采用改进的“sqtwolog”准则[22]，计算公式见式(13)，阈值函数选软阈值．选择降噪后信号的RMSE和SNR作为纯净信号已知时判断最优分解尺度的指标，计算结果如图3所示．为方便对比，RMSE、SNR结果进行对数运算．

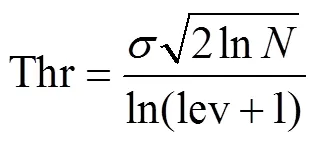
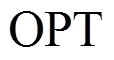
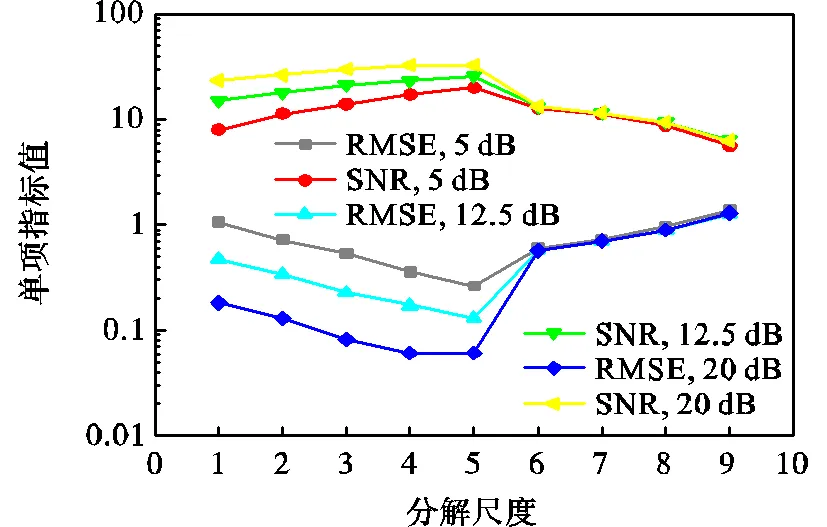
图3 不同信噪比时单项指标值

表1 纯净信号已知时的综合评价指标值

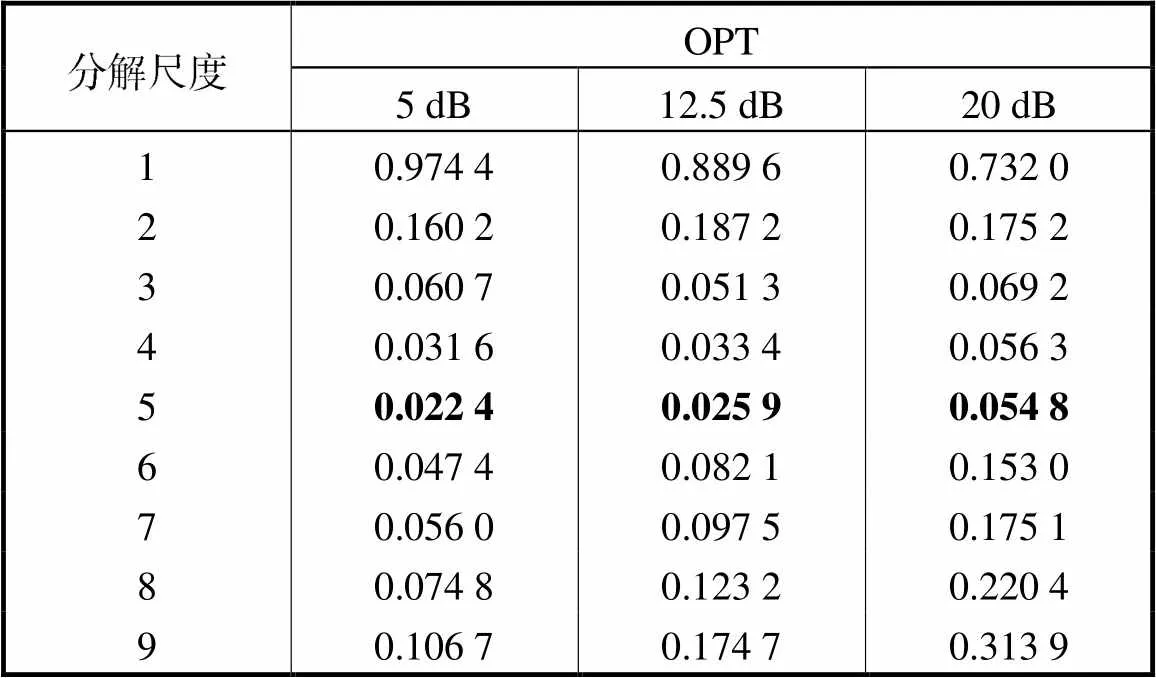
Tab.1 Comprehensive evaluation index when the pure signal is known

3.2 纯净信号未知

表2 纯净信号未知时的不同评价指标

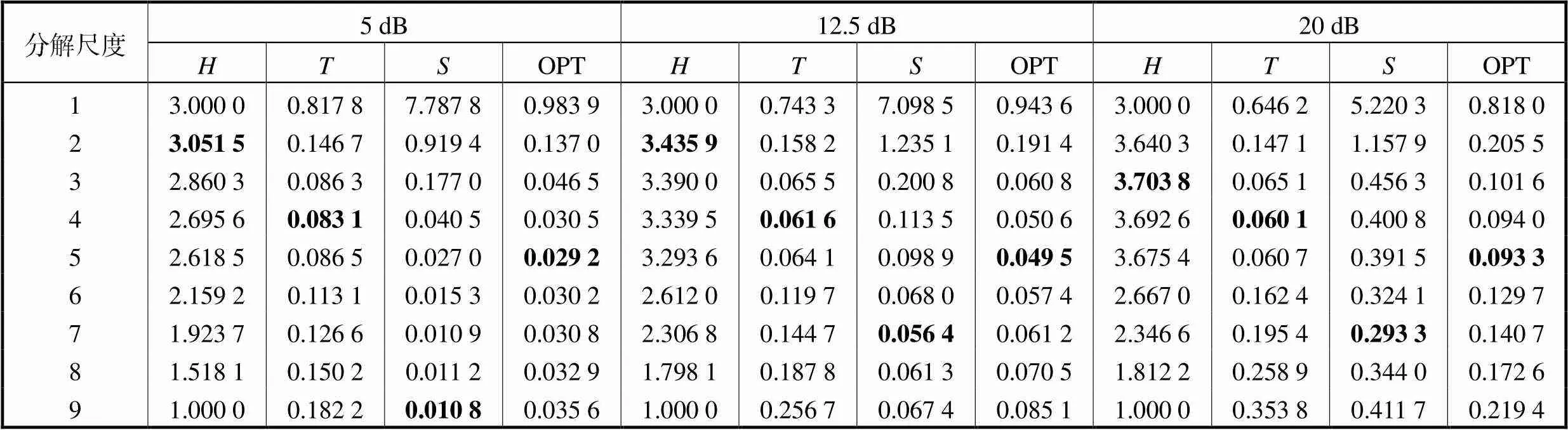
Tab.2 Different evaluation indexes when the pure signal is unknown

利用综合评价指标OPT确定最优分解尺度的证明过程已完毕，考虑到最优小波基函数的验证过程与分解尺度类似，此处不再赘述，仅给出信噪比为12.5dB时的结果并列于表3，其中小波基函数选择具有较好正交性和紧支撑性的db与sym小波[23].由表3可以看出，均方根误差与信噪比在小波基函数取“db8”时有极小值，因此单项指标确定的最优基函数为“db8”．指标OPT在纯净信号已知和未知情况下均在“db8”时取得极小值，与正确最优值结果一致，因此可以说明指标OPT同样适用于最优小波基函数的确定．

表3 不同小波基函数对应的单项和综合指标值

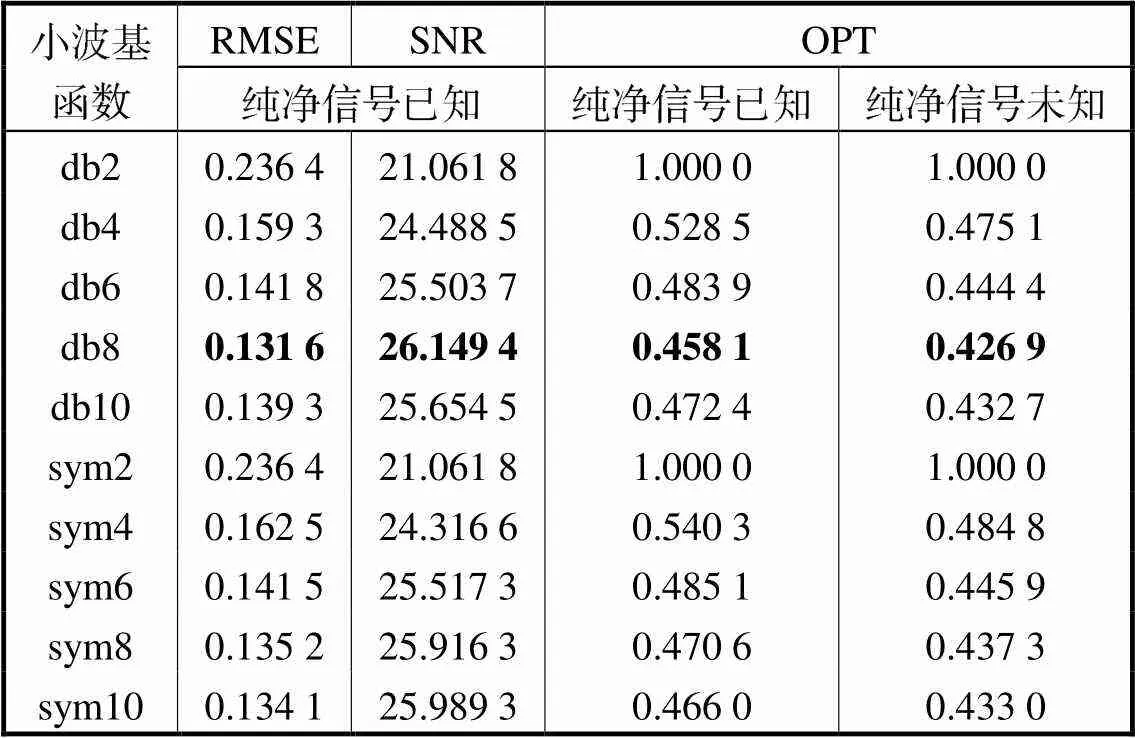
Tab.3 Single and composite index values corresponding to different wavelet basis functions

3.3 与其他方法比较

4 工程实例应用

为探究本文所提基于组合赋权法综合评价指标的小波阈值降噪在实际工程GNSS监测信号中的应用，选取采用GNSS-RTK技术对天津广播电视塔(简称天塔)进行实时动态变形监测试验的部分数据进行分析，其中采样频率为10Hz，监测数据变化规律如图4所示．从图中可以看出天塔结构的真实振动位移被噪声“吞噬”，影响反映真实位移的特征提供，因此需对其进行一定的降噪处理．首先利用传统评价指标确定最优分解尺度，结果如表4所示．根据传统评价准则比较每个指标的值，确定的最优分解尺度(表中加粗显示)既不唯一又较为极端、不合实际．因此传统评价指标不再适用．接下来利用本文所提综合评价指标OPT选择最优分解尺度和小波基函数来对原始信号进行降噪．小波各参数与第3节选取一致，指标OPT的计算结果如图5所示．从图5可以看出，当分解尺度为6、小波基函数为“db10”时，指标OPT有极小值，因此最优分解尺度为6层，最优小波基函数为“db10”．相比传统评价指标，本文综合评价指标计算过程中出现极值，使确定过程更科学、结果更准确．

由于GNSS监测信号的纯净信号是未知的，为进一步说明综合评价指标OPT的有效性，以不同分解尺度为例进行说明．通过比较与分解尺度6相邻的两个分解尺度5和7下的降噪后信号(见图6)可以得出，3种尺度下最大位移由原始信号的24.34mm分别降到18.45mm、16.76mm、15.69mm，噪声都得到去除，但分解尺度为5时的降噪信号仍存在一定程度的噪声，“毛刺”现象明显，属于欠降噪．而分解尺度为7时的振动位移幅值虽减小得最多，但此时的信号已失真严重，原始信号的细节部分被过度抹去，不满足实际需求，属于过降噪．相比尺度5、7，尺度6的降噪信号在去除噪声与保留原始信号的有效信息方面得到了很好的平衡，属于最优降噪，同时也从时域角度表明了本文所提综合评价指标OPT在工程应用中的可行性．

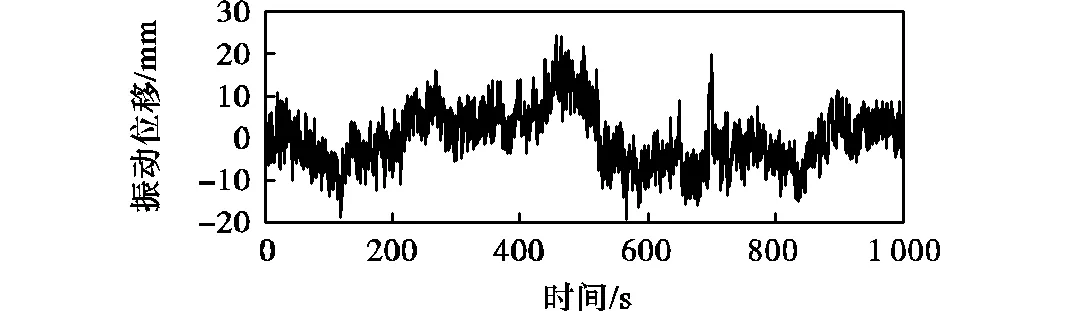
图4 GNSS监测信号

表4 工程实例中不同分解尺度对应的传统指标值

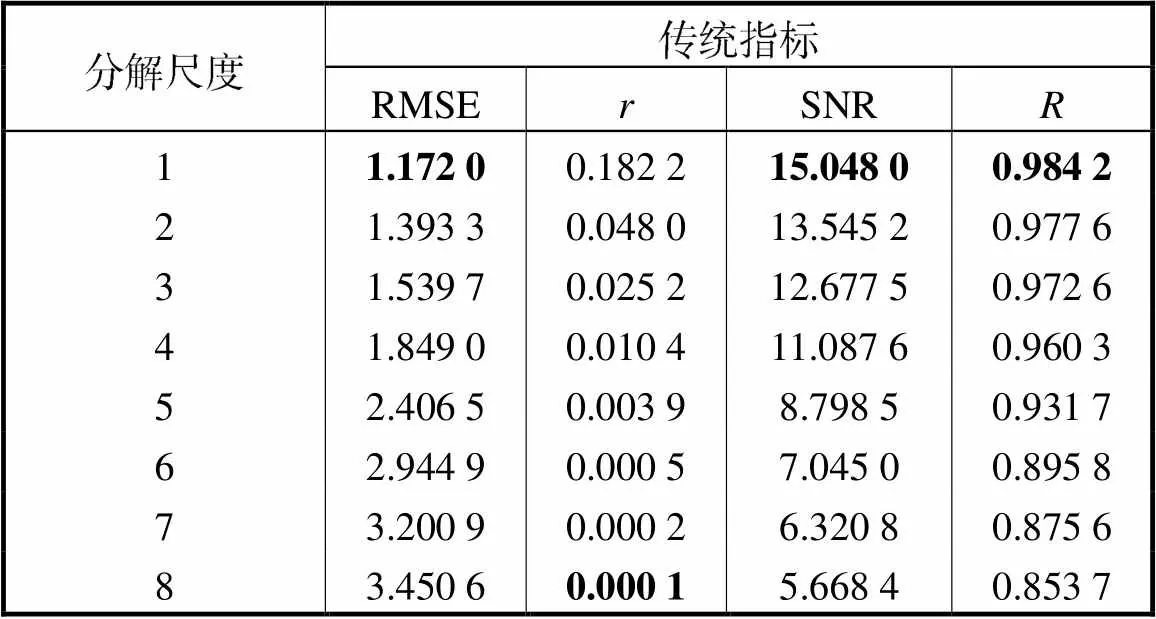
Tab.4 Traditional index values corresponding to differ-ent decomposition scales in the engineering exam-ple

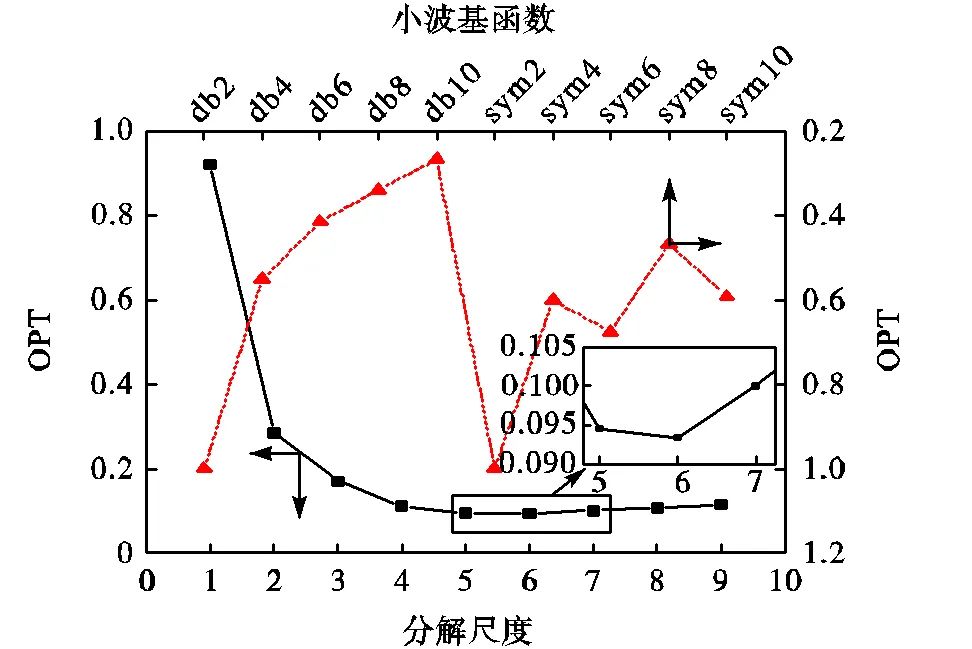
图5 不同分解尺度和小波基函数的OPT

图6 不同分解尺度降噪后信号

图7为原始信号与降噪后信号的频谱变化规律图.观察可以看出，利用本文方法确定的小波参数最优值降噪后的信号与原始信号相比，基本完美滤除了高频噪声及部分低频噪声，并有效保留了低频有用信息.另外，原始信号识别的结构振动频率为0.1580Hz，而通过最优小波参数降噪后的信号识别出的结构振动频率为0.1550Hz，误差仅为1.9%．同时，从频域角度也验证了本文综合评价指标的可靠性.

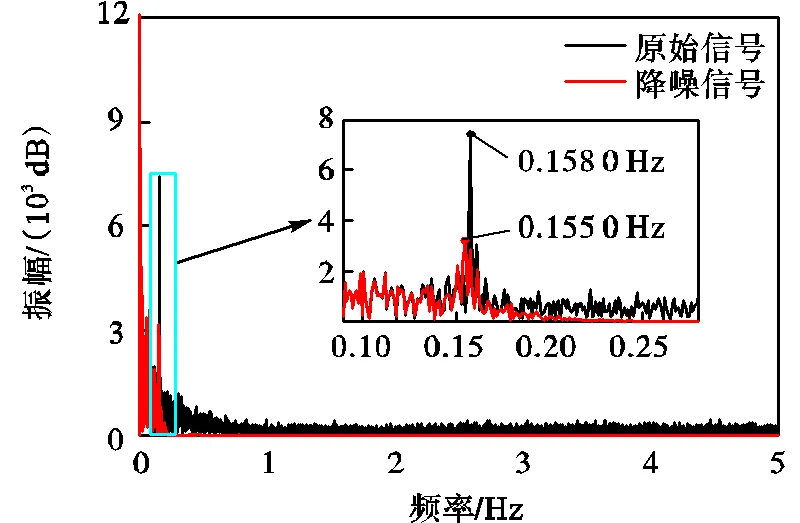
图7 原始信号和降噪后信号的频谱

5 结论

本文针对已有小波降噪质量评价指标的不足，提出一种新的基于组合赋权法的综合评价指标OPT.通过仿真信号和工程实例分析，所提综合指标表现出很好的优越性和适用性，主要得到以下结论．

(1) 用熵权法和变异系数法对均方根误差与平滑度的归一化值组合赋权的方法，克服了单一赋权法的缺陷，使两单项指标的权重分配更加合理和客观，进而使综合评价指标更能精确识别小波参数的最优值.

(2) 相比其他综合评价指标，从单项指标组成分量的选取到分解尺度和小波基函数最优值确定的过程中，本文所提综合评价指标的物理含义更明确，准确性更高，普适性更好．

(3) 所提综合评价指标在GNSS监测信号的降噪应用中也准确提取出结构的真实振动位移，可为 后续动态变形预测奠定基础，具有很好的工程应用 意义.

本文所提综合评价指标主要用于确定小波阈值降噪中分解尺度和小波基函数的最优值，然而小波降噪效果还受阈值准则和阈值函数的影响，因此未来的研究将对上述两参数最优值的确定进一步展开．

［1］ Lovse J W，Teskey W F，Lachapelle G，et al. Dynamic deformation monitoring of tall structure using GPS technology[J]. Journal of Surveying Engineering，1995，121(1)：35-40.

［2］ Xiong C B，Niu Y B，Li Z. An investigation of the dynamic characteristics of super high-rise buildings using real-time kinematic-global navigation satellite system technology[J]. Advances in Structural Engineering，2018，21(5)：783-792.

［3］ 熊春宝，张雪芳，牛彦波，等. 一种基于RTK-GNSS技术的大跨径悬索桥动态特性分析方法[J]. 天津大学学报(自然科学与工程技术版)，2019，52(7)：699-708.

Xiong Chunbao，Zhang Xuefang，Niu Yanbo，et al. A method for analyzing the dynamic characteristics of a long-span suspension bridge based on RTK-GNSS technique[J]. Journal of Tianjin University(Science and Technology)，2019，52(7)：699-708(in Chinese).

［4］ 黄丁发，陈永奇，丁晓利，等. GPS高层建筑物常荷载振动测试的小波分析[J]. 振动与冲击，2001，20(1)：12-15.

Huang Dingfa，Chen Yongqi，Ding Xiaoli，et al. Waveletbased analysis technique for the monitoring of tall structure under normal loading using GPS[J]. Journal of Vibration and Shock，2001，20(1)：12-15(in Chinese).

［5］ 王中宇，夏新涛，朱坚民. 非统计原理及其工程应用[M]. 北京：科学出版社，2005.

Wang Zhongyu，Xia Xintao，Zhu Jianmin. Statistical Principle and Its Application in Engineering[M]. Beijing：Science Press，2005(in Chinese).

［6］ 李宗春，邓 勇，张冠宇，等. 变形测量异常数据处理中小波变换最佳级数的确定[J]. 武汉大学学报(信息科学版)，2011，36(3)：285-288.

Li Zongchun，Deng Yong，Zhang Guanyu，et al. Determination of best grading of wavelet transform in deformation measurement data filtering[J]. Geomatics and Information Science of Wuhan University，2011，36(3)：285-288(in Chinese).

［7］ 陶 珂，朱建军. 多指标融合的小波去噪最佳分解尺度选择方法[J]. 测绘学报，2012，41(5)：749-755.

Tao Ke，Zhu Jianjun. A hybrid indicator for determining the best decomposition scale of wavelet denoising[J]. Acta Geodaetica et Cartographica Sinica，2012，41(5)：749-755(in Chinese).

［8］ 朱建军，章浙涛，匡翠林，等. 一种可靠的小波去噪质量评价指标[J]. 武汉大学学报(信息科学版)，2015，40(5)：688-694.

Zhu Jianjun，Zhang Zhetao，Kuang Cuilin，et al. A reliable evaluation indicator of wavelet de-noising[J]. Geomatics and Information Science of Wuhan University，2015，40(5)：688-694(in Chinese).

［9］ 王 旭，王 昶. 一种基于熵权法的小波去噪复合评价指标[J]. 大地测量与地球动力学，2018，38(7)：698-702，718.

Wang Xu，Wang Chang. A kind of wavelet de-noising composite evaluation index based on entropy method[J]. Journal of Geodesy and Geodynamics，2018，38(7)：698-702，718(in Chinese).

［10］ 高 山，李沁声. 基于熵权的小波去噪评价指标[J]. 测绘与空间地理信息，2019，42(8)：1-4，7.

Gao Shan，Li Qinsheng. Evaluation index of wavelet de-noising based on entropy weight[J]. Geomatics & Spatial Information Technology，2019，42(8)：1-4，7(in Chinese).

［11］ 邵 旋，康兴无，王旭平，等. 基于多元信息融合的小波降量综合评估指标[J]. 兵器装备工程学报，2020，41(12)：155-160.

Shao Xuan，Kang Xingwu，Wang Xuping，et al. Comprehensive evaluation index of wavelet denoising quality based on multi-information fusion[J]. Journal of Ordnance Equipment Engineering，2020，41(12)：155-160(in Chinese).

［12］ 李红延，周云龙，田 峰，等. 一种新的小波自适应阈值函数振动信号去噪算法[J]. 仪器仪表学报，2015，36(10)：2200-2206.

Li Hongyan，Zhou Yunlong，Tian Feng，et al. Wavelet-based vibration signal de-noising algorithm with a new adaptive threshold function[J]. Chinese Journal of Scientific Instrument，2015，36(10)：2200-2206(in Chinese).

［13］ 余 腾，胡伍生，吴 杰，等. 基于小波阈值去噪与EMD分解方法提取润扬大桥振动信息[J]. 振动与冲击，2019，38(12)：264-270.

Yu Teng，Hu Wusheng，Wu Jie，et al. Extraction of runyang bridge vibration information based on a fusion method of wavelet threshold denoising and EMD decomposition[J]. Journal of Vibration and Shock，2019，38(12)：264-270(in Chinese).

［14］ 何友福. 基于小波去噪优化的变形监测数据处理及预测研究[D]. 成都：成都理工大学地球科学学院，2019.

He Youfu. Research on Data Processing and Prediction of Deformation Monitoring Based on Wavelet Denoising Optimization[D]. Chengdu：College of Geosciences，Chengdu University of Technology，2019(in Chinese).

［15］ 王 维，张英堂，任国全. 小波阈值降噪算法中最优分解层数的自适应确定及仿真[J]. 仪器仪表学报，2009，30(3)：526-530.

Wang Wei，Zhang Yingtang，Ren Guoquan. Adaptive selection and simulation of optimal decomposition level in threshold de-noising algorithm based on wavelet transform[J]. Chinese Journal of Scientific Instrument，2009，30(3)：526-530(in Chinese).

［16］ 钟建军，宋 健，由长喜，等. 基于信噪比评价的阈值优选小波去噪法[J]. 清华大学学报(自然科学版)，2014，54(2)：259-263.

Zhong Jianjun，Song Jian，You Changxi，et al. Wavelet de-noising method with threshold selection rules based on SNR evaluations[J]. Journal of Tsinghua University(Science and Technology)，2014，54(2)：259-263(in Chinese).

［17］ 周 建，向北平，倪 磊，等. 基于Shannon熵的自适应小波包阈值函数去噪算法研究[J]. 振动与冲击，2018，37(16)：206-211，240.

Zhou Jian，Xiang Beiping，Ni Lei，et al. A study on adaptive wavelet packet threshold function de-noising algorithm based on Shannon entropy[J]. Journal of Vibration and Shock，2018，37(16)：206-211，240(in Chinese).

［18］ 戴吾蛟，丁晓利，朱建军，等. 基于经验模式分解的滤波去噪法及其在GPS多路径效应中的应用[J]. 测绘学报，2006，35(4)：321-327.

Dai Wujiao，Ding Xiaoli，Zhu Jianjun，et al. EMD filter method and its application in GPS multipath[J]. Acta Geodaetica et Cartographica Sinica，2006，35(4)：321-327(in Chinese).

［19］ Cheng Q Y. Structure entropy weight method to confirm the weight of evaluating index[J]. Systems Engineer-ing—Theory & Practice，2010，30(7)：1225-1228.

［20］ 刘舒馨，唐祥云，张 燚，等. 基于熵权和变异系数组合赋权法的耕地质量评价实证研究[J]. 国土与自然资源研究，2016(4)：45-50.

Liu Shuxin，Tang Xiangyun，Zhang Yi，et al. Empirical research on evaluation of quality of cultivated land and entropy variation coefficient combination weighting method[J]. Territory & Natural Resources Study，2016(4)：45-50(in Chinese).

［21］ 陈 雪. 基于投影寻踪方法的建筑业企业高质量发展评价研究[D]. 哈尔滨：哈尔滨工业大学土木工程学院，2020.

Chen Xue. Research on Evaluation of High Quality Development of Construction Enterprises Based on Projection Pursuit Method[D]. Harbin：College of Civil Engineering，Harbin Institute of Technology，2020(in Chinese).

［22］ Kasambe P V，Rathod S S. VLSI wavelet based denoising of PPG signal[J]. Procedia Computer Science，2015，49(1)：282-288.

［23］ 戴海亮，孙付平，姜卫平，等. 小波多尺度分解和奇异谱分析在GNSS站坐标时间序列分析中的应用[J]. 武汉大学学报(信息科学版)，2021，46(3)：371-380.

Dai Hailiang，Sun Fuping，Jiang Weiping，et al. Application of wavelet decomposition and singular spectrum analysis to GNSS station coordinate time series[J]. Geomatics and Information Science of Wuhan University，2021，46(3)：371-380(in Chinese).

Investigation on Comprehensive Evaluation Index of Wavelet Threshold Denoising Based on Combination Weighting Method

Xiong Chunbao，Pang Hongxing

(School of Civil Engineering，Tianjin University，Tianjin 300072，China)

The traditional wavelet denoising effect evaluation indexes，such as the root mean square error，signal-to-noise ratio(SNR)，correlation coefficient，and smoothness，are suitable for known pure signals. However，the pure state of a monitored signal is often unknown in practical applications. To solve the limitations of traditional evaluation indexes，a comprehensive evaluation index based on the combination weighting method is proposed in this study. First，on the basis of theoretical analysis and case verification，the index component was determined as the root mean square error and smoothness from the perspectives of increase-decrease characteristics and physical meaning. Then，the threshold maximum method was used to normalize the two indicators. Finally，the entropy weight method and variation coefficient method were applied to calculate the corresponding weights of the normalized values of root mean square error and smoothness，and the linear combination was added. The decomposition scale and wavelet basis function corresponding to the minimum value of the comprehensive evaluation index were the optimal wavelet parameters. The analysis of three SNR(5，12.5，and 20dB)simulation signals shows that the optimal decomposition scale and wavelet basis function are identified，and the noise reduction effect is optimal. Compared with other comprehensive indicators，the accuracy and universality of the index are better. In addition，this index can be applied to GNSS monitoring signals，which has certain engineering value.

wavelet threshold denoising；comprehensive evaluation indicators；entropy weight method；variation coefficient method；combination weighting

10.11784/tdxbz202109014

P228

A

0493-2137(2022)12-1300-09

2021-09-08；

2021-10-25.

熊春宝（1964—  ），男，博士，教授，luhai_tj@163.com.

庞红星，hongxingpang@tju.edu.cn.

国家自然科学基金资助项目(61971037).

Supported by the National Natural Science Foundation of China(No. 61971037).

(责任编辑：樊素英)