水流对复合筒型基础波浪爬升影响机制的数值模拟研究
于通顺,宋昊阳,刘梅梅,章誉天
水流对复合筒型基础波浪爬升影响机制的数值模拟研究
于通顺1,宋昊阳1,刘梅梅2,章誉天3
(1. 中国海洋大学工程学院,青岛 266100;2. 中交四航工程研究院有限公司,广州 510230;3.重庆市垫江县水利局,重庆 408300)
复合筒型基础(CBF)是一种新型的海上风电基础,当波浪海流与其大尺寸反弧段作用时,会产生复杂的波浪爬升现象,严重威胁基础外平台的安全,因此,有必要对波流作用下复合筒型基础的波浪爬升现象开展研究.首先,采用RNG-模型建立了波流与复合筒型基础相互作用的数值水槽.其次,基于试验数据验证了数值模型的准确性.最后,探究了波流作用下复合筒型基础周围的波浪爬升规律,揭示了不同流速比cw下水流对波浪爬升的贡献.研究发现:①波浪单独作用下复合筒型基础前方水体回落到最低点时,水质点的运动方向均为斜向下方,而在波流联合作用时,复合筒型基础前端形成漩涡,背面的水质点将朝着不同的方向进行扩散;②波浪单独作用时,复合筒型基础背浪面水体呈“公鸡尾”状,而波流联合作用时,复合筒型基础背浪面水体呈“双髻鲨”状;③当波陡参数为0.025时,流速比由0.46增大到0.59时,波浪爬升高度增大约0.55倍.
复合筒型基础;波浪爬升;波流相互作用;数值模拟
2020年,我国提出力争于2030年前二氧化碳排放达到峰值,2060年前实现碳中和.我国海上风能资源丰富,可开发量达7.5亿千瓦[1],在“碳中和”的背景下海上风电迎来历史性的发展机遇.海上风电基础处于复杂的海洋环境中,波流作用于风电基础时会产生强烈的波浪爬升现象(如图1所示),引发靠船设备及工作平台的冲击破坏,海上风电基础波浪爬升的研究成为近年来海洋工程领域的研究热点.

图1 海上风电基础波浪爬升
复合筒型基础[2-5](如图2所示)作为一种新型的海上风电基础,因其抗倾覆能力和对软土地基的适应能力强等优势受到越来越多的关注.复合筒型基础大尺寸的反弧段结构及宽浅式的筒裙为其包括水动力特征、承载特性、传力规律等工作性能的明确带来了挑战,有学者对复合筒型基础承载性能[6]、应力响应及传力特性[7]、地基冲刷[8-9]等方面开展了大量研究,然而不同波流环境下复合筒型基础波浪爬升特征尚缺乏系统性分析,这也在一定程度上影响了复合筒型基础适用水深的确定,增加了靠船设备及平台的运行风险,限制了其大规模推广.因此,研究复杂波流环境中复合筒型基础的波浪爬升特性很有必要.

图2 海上风电复合筒型基础
关于波流作用下海上风电基础波浪爬升的研究已经展开,这些研究的对象主要集中于单桩基础[10-13]、多桩基础[14]及重力式基础[15-16],针对复合筒型基础这种新型结构波浪爬升的研究相对较少.通过单桩基础波浪爬升的研究结果[10-11],可以对复合筒型基础上波浪爬升特征有初步的了解,但是考虑到复合筒型基础大尺寸反弧段结构这种复杂的边界条件,复合筒型基础周围波浪爬升过程中流场特征会更加复杂. Yu等[17]基于物理模型试验的方法探究了波浪单独作用下复合筒型基础周围的爬升特征,获取了不同工况下的最大爬升高度.然而,复合筒型基础波浪爬升过程中的水动力机制尚需深入探究,水流对波浪爬升影响机理的研究也需进一步开展.因此,为深入探讨波浪、水流作用过程中复合筒型基础波浪爬升机制,本文借鉴其他风电基础波浪爬升的数值模拟研究方 法[13-15],建立了波流与复合筒型基础相互作用的数值模型,研究了海流对复合筒型基础爬升特性的影响,阐述了海流和不同的波浪参数对复合筒型基础附近波面扰动的影响.
1 控制方程及求解方法
本文中涉及的流体为不可压缩黏性牛顿流体,选用连续性方程和不可压缩运动流体的N-S动量方程作为流体运动的控制方程,其具体表达式如下:



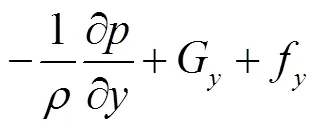
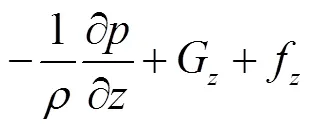
为了准确模拟波浪、水流和结构物相互作用时流体产生的变形破碎,本文采用重组化RNG-模型,其表达式如下:



表1 RNG-模型系数取值

Tab.1 Coefficient value of RNGk-ε model

2 三维数值波流水槽
2.1 三维数值波流水槽的建立
建立计算区域大小(长×宽×高)为10.2m×3m× 0.37m的数值波浪水槽,数值波浪水槽最左侧是波流边界(wave-current),最右侧是出流边界(outflow),上、下两侧边界条件为对称边界(symmetry),底部边界为壁面(wall),顶部边界为压力(specified pressure),如图3所示.为了减少波浪的反射,在最右侧出流边界前放置了大小为2m×3m×0.37m的消波块,左侧的阻尼系数定为1,右侧的阻尼系数定为4.2.
2.2 网格划分及网格独立性验证
数值模拟的准确性与网格划分结果息息相关,因此,为了更好地分析复合筒型基础周围的波浪爬升效应,需要对波高部分的网格进行加密,本文选用3种算例,在波高部分加密的网格形式为细网格、中网格、粗网格,如表2所示.图3所示水槽内先不放置复合筒型基础,提取波高()0.06m、周期()1.25s、水深()0.25m的波浪作用下基础位置处的波面时程曲线,如图4所示.比较发现中等网格和细网格的计算结果相差不大,粗网格的计算结果与其他两种相差较大.所以,综合考虑计算精度和计算速度,选用中网格对波高部分进行加密.

图3 三维数值波浪水槽
表2 网格数量和尺寸
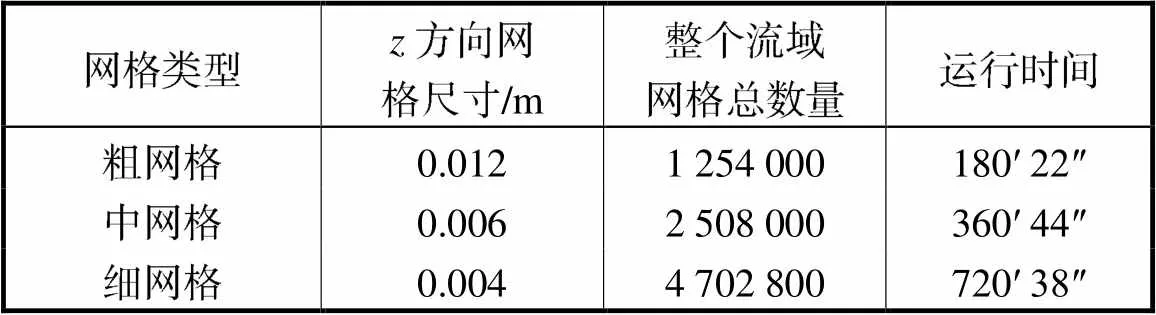
Tab.2 Meshnumber and size
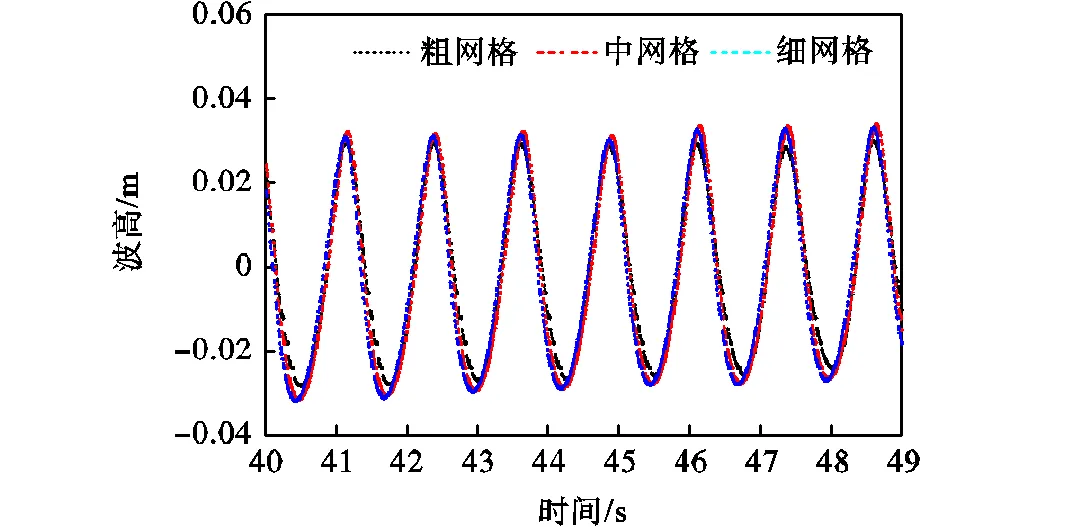
图4 3种网格尺寸的自由面高程历时曲线
2.3 三维数值波流水槽验证
提取中等网格状态下波高0.06m、周期1.25s、水深0.25m的入射波浪作用下距离水槽入口边界5m处波面时程曲线与理论值进行对比如图5所示,可以看出计算值与理论值吻合较好,表明此网格状态下水槽准确性较高.
提取波高0.06m、周期1.4s、水深0.25m时不同流速下距造波板5m处波高的计算值与理论值[18]对比如图6所示.

图5 自由波面计算值与理论值的时程曲线

图6 波流作用下波高的计算值与理论值的对比
为了验证数值水槽中基础周围波浪爬升的准确性,将复合筒型基础模型放置于距离造波板5m处,将波高0.06m、周期1.4s、水深0.25m的波浪与3种流速(0.12m/s、0.16m/s、0.20m/s)的水流共同作用下基础最大波浪爬升高度与已有试验数据[17]对比,如图7所示.可以看出,计算值与试验值的波浪爬升高度误差在5%以内,说明此数值水槽能够较好地模拟复合筒型基础上的波浪爬升特征.
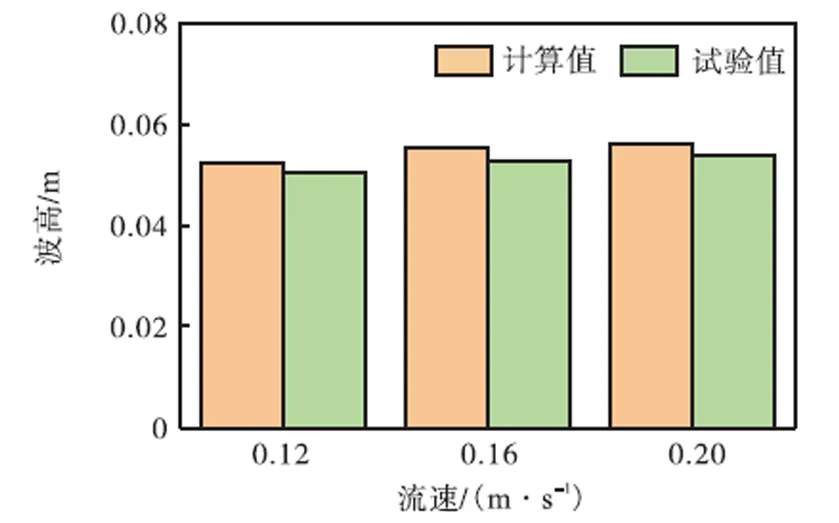
图7 复合筒型基础A1处最大波浪爬升高度计算值和试验值的对比
2.4 虚拟观测点的位置
为了深入研究复合筒型基础周围的波浪爬升特性,在其周围设置6组浪高仪,相邻两组之间的角度为36°,观测点的具体布置如图8所示.浪高仪至复合筒型基础中心的水平距离如表3所示.
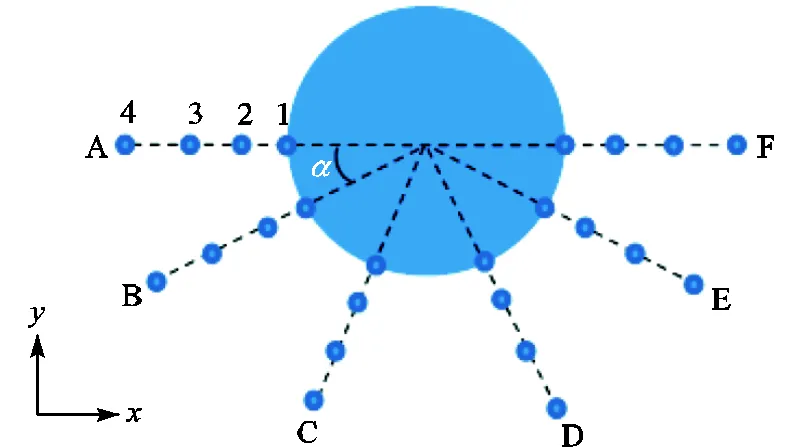
图8 沿径向分布的虚拟浪高仪
表3 虚拟浪高仪的位置

Tab.3 Positions of virtual wave probes
注:为复合筒型基础在其相应水深下对应的水面交界处筒的半径,即0.25m水深下=8.07cm.
2.5 工况设置
波浪爬升的数值模拟采用如表4所示工况,分波浪单独作用和波流(同向传播)共同作用两组.波浪单独作用时选取了两组波陡(0.025、0.035),波流共同作用时选取了2种海流速度(0.12m/s、0.20m/s),波陡变化范围为0.025~0.035.
表4 波浪爬升工况
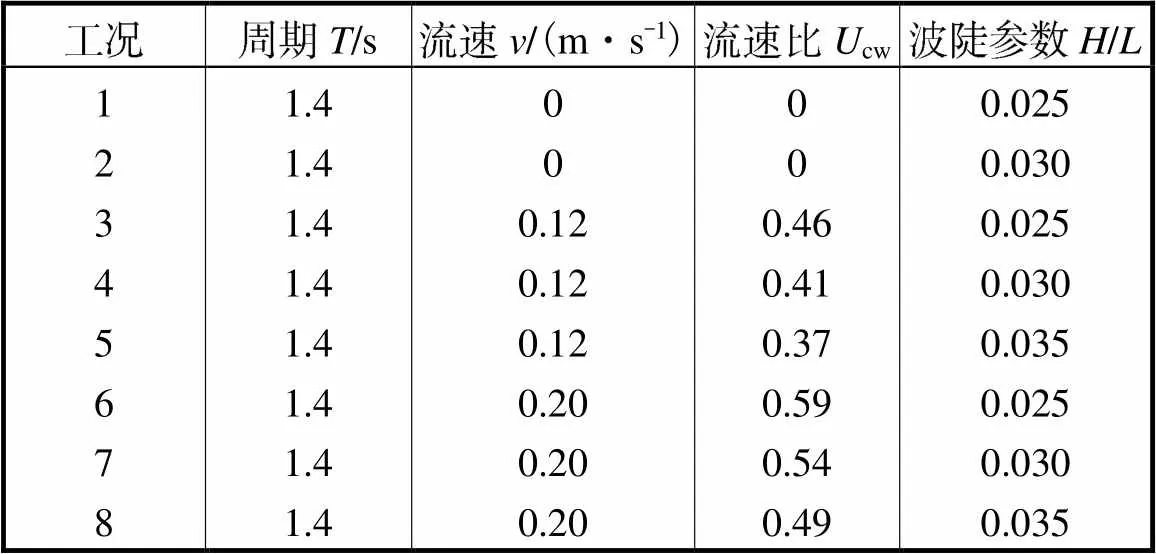
Tab.4 Wave conditions for wave run-up
注:流速比cw=c/(c+wm),wm为波浪诱导水质点流速幅值,c为水流流速;cw=0代表单独波浪情况,cw=1代表单独水流情况.
3 结果与讨论
3.1 波流作用下复合筒型基础周围流场特性
3.1.1 基础周围水质点速度分布
波浪单独作用及波流共同作用下复合筒型基础周围竖向剖面流场分布如图9、图10所示.从图9中可以看出:①由于复合筒型基础的阻碍作用,水体的动能转化为势能从而迅速向上爬升;②当其前端波浪爬升至最高点时,峰值附近的水体速度接近于零(区域Q),虽然仍有少量质点的向上爬升,但大部分水质点的矢量方向为斜向下,说明水体正在回落,这与单铁兵等[11]针对立柱所得到的规律一致.
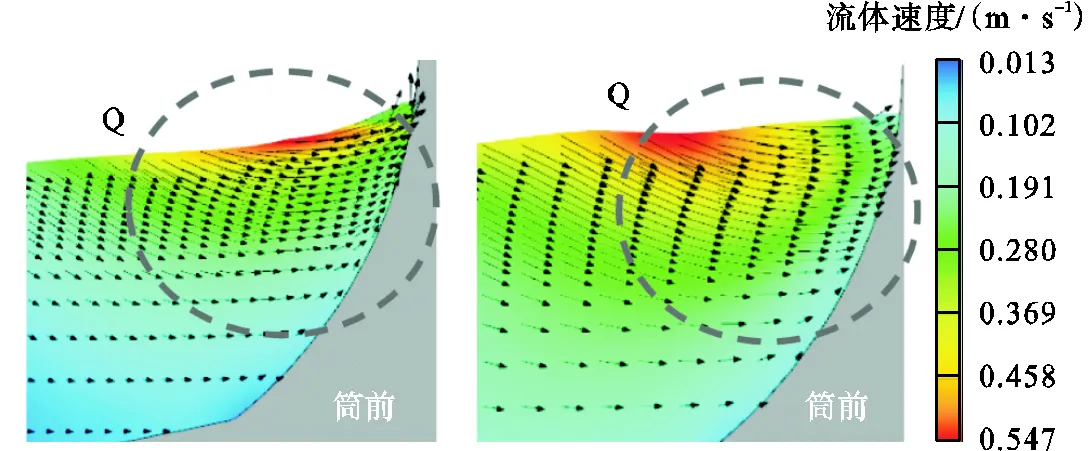
(a)Ucw=0(工况2) (b)Ucw=0.54(工况7)
从图10可以看出:①波流共同作用下,当前端波浪回落到较低位置时,复合筒型基础前端流体质点紧靠反弧段产生顺时针方向旋转的漩涡(如区域S1),出现这种情况的原因可能是由于入射波浪遇到复合筒型基础反射后的水质点、沿复合筒型基础两侧回流的水体,这两种水体的水质点矢量方向不同,发生碰撞,再加上海流的作用,产生强烈的非线性作用.而仅有波浪作用时,水质点的运动比较规律,都斜向左下方运动,没有出现明显的漩涡现象;②当复合筒型基础前端波浪回落到最低点时,复合筒型基础背浪面水位上升,在波流共同作用下,复合筒型基础背面产生漩涡,图(b)中的漩涡靠近壁面,水质点沿着不同方向迅速扩散,如图(b)中S2区域所示,而在图(a)中水质点的运动比较规律,矢量方向都为斜向右下方.因此可以看出,海流的存在将在一定程度上增加复合筒型基础周围波面的扰动.
3.1.2 基础周围流场分布
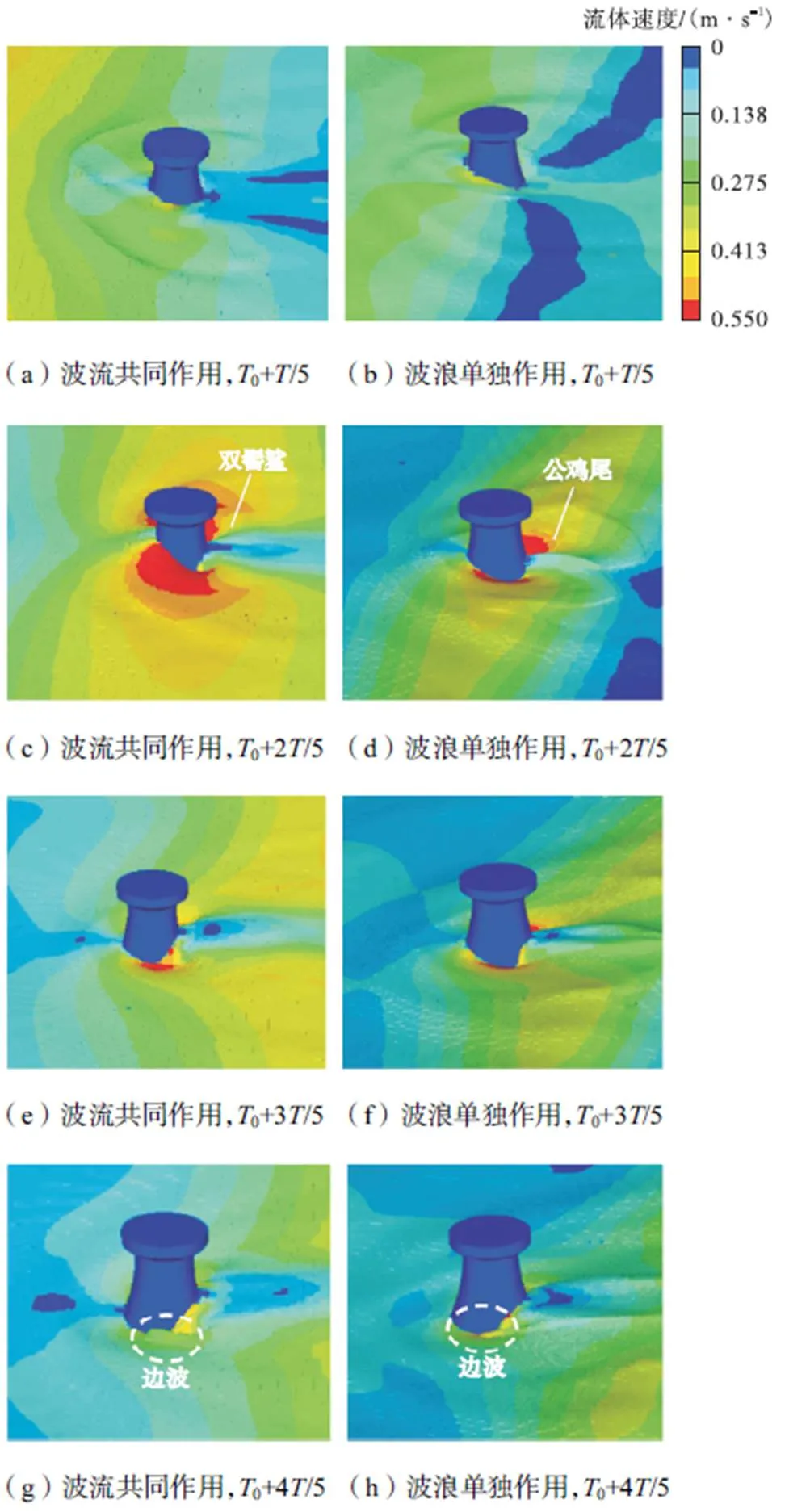
取初始时刻0=40s、周期=1.4s.波流共同作用及波浪单独作用下复合筒型基础周围流场分布如图11所示.从波流共同作用时复合筒型基础周围的流场分布可以看出:在0+/5时,(见图(a)、(b))波峰到达复合筒型基础前沿,使复合筒型基础两侧出现正向传播的边缘波,并且对称分布.当波峰穿过复合筒型基础时,由于基础的阻碍作用,复合筒型基础前方水体壅高,动能转化为爬升势能,前方的自由表面以对称形状向外扰动和辐射;0+2/5(见图(c)、(d))时波浪沿着复合筒型基础壁面绕射,两股波浪沿着复合筒型基础的两侧向后面传播,在复合筒型基础背面进行叠加,波面迅速放大;0+3/5和0+4/5(见图(e)~(h))时,当复合筒型基础背浪面波速接近于零时,水体开始回落,波浪沿着复合筒型基础两侧进行回流,这时,由于基础前端水体的速度比较大,并且水质点的运动方向与波的传播方向相反,波浪会向着复合筒型基础迎浪面迅速移动,形成边波;0+(见图(i)、(j))时,接近入射波谷到达的相位,扰动被扫离基础以产生一对对称但非同心的波面,与Sun等[19]在数值水槽中所观察到的Type-2散射波场类似.反方向流的边波将与入射波浪或海流相互作用引起波面的非线性扰动和大变形,并且波形不断向远方传播;最后,由于水体能量的不断耗散,水质点的速度也会不断减小,波面扰动效应的影响逐渐变小.波浪单独作用时,复合筒型基础周围的流场分布,与波流联合作用时的情况进行比较得出:①两者水体回荡过程相似,比较(c)、(d)图可以看出,波浪单独作用时,复合筒型基础背浪面水体呈“公鸡尾”状,而波流联合作用时,复合筒型基础背浪面水体呈“双髻鲨”状;②复合筒型基础背面的水体回落,水质点的运动方向与波的传播方向相反,波浪会向着复合筒型基础迎浪面迅速移动,将会形成边波,波浪单独作用时,水体自由表面分布比较光滑和均匀,水体没有出现较大的变形,波流联合作用时的波面速度变化大,扰动剧烈,扰动范围约为2,说明海流在一定程度上增加波面的非线性特征.
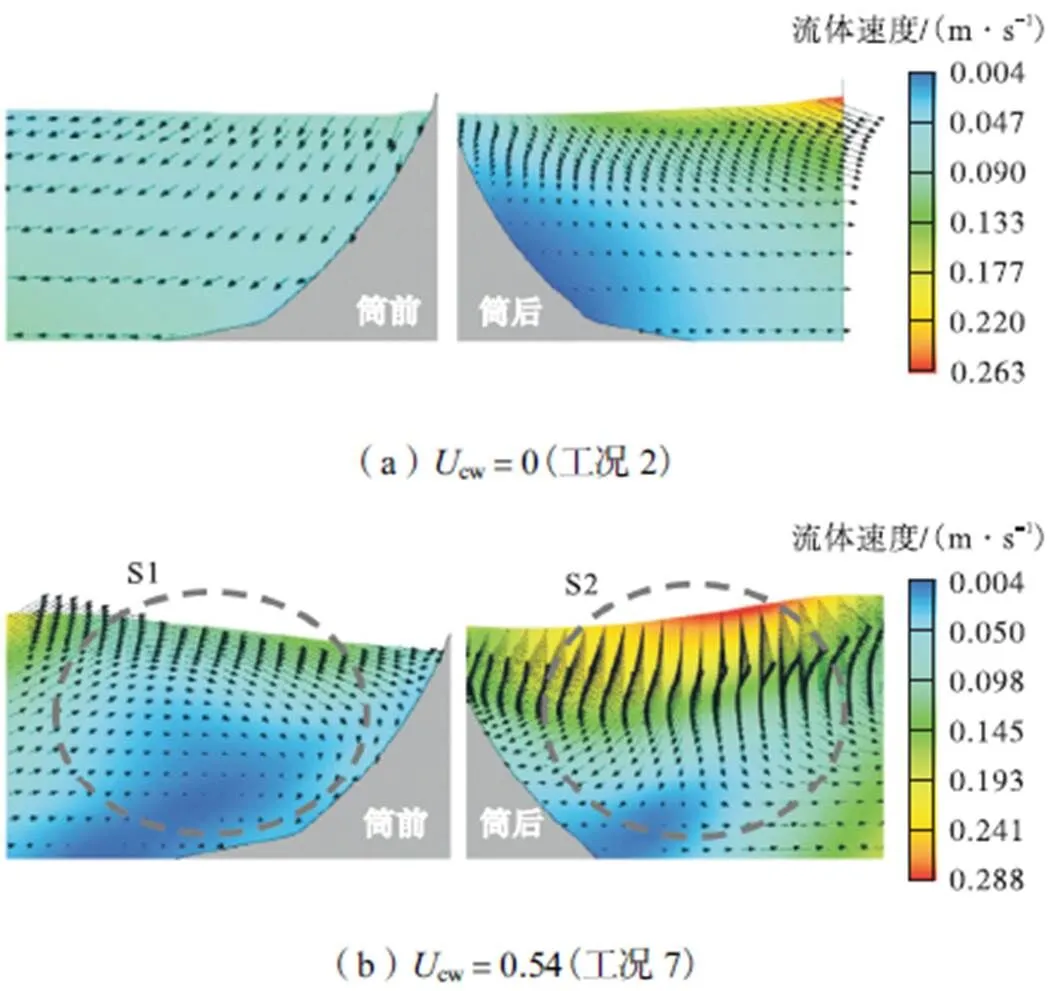
图10 波浪回落到最低点时复合筒型基础周围竖向剖面流场分布
3.2 水流对复合筒型基础波浪爬升高度的影响
本文中对波浪爬升值Ru用入射波幅/2进行了无量纲化处理.图12为波浪沿着复合筒型基础反弧段在0°、36°、72°、108°、144°和180°时的爬升分布规律.从图中可以看出:①波浪爬升倍数Ru/(/2)的最大值都出现在复合筒型基础迎浪面正中心即0°附近,并且在同一速度条件下,随着波陡增大,爬升倍数也相应增大.波浪沿着复合筒型基础两侧传播过程中爬升倍数逐渐降低,但在背浪面108°附近又开始增大,出现这种现象的原因是波浪遇到复合筒型基础阻挡后,会有两股波浪沿着复合筒型基础侧面继续传播,在复合筒型基础背面进行叠加,使得波面较高;②波浪爬升倍数的最小值约在108°处,随着水流流速的增大,波浪爬升倍数的最小值也相应增大,这是因为海流和波浪的相互作用加大了水体的能量,从而使得转化的势能更大导致了爬升倍数增大.这与Lin等[16]得出单桩支撑结构的最大爬升高度出现在0°的位置,而相对最小的爬升高度分别位于112.5°附近基本一致;③波流联合作用时,144°到180°附近的爬升倍数变化较为平缓,而波浪单独作用时,爬升值变化幅度较大,与图11(c)、(d)相对应;④复合筒型基础迎浪侧的相对爬升倍数随波陡增大而增大,而在复合筒型基础背浪一侧,对于更高的波陡相对爬升倍数更小.这与Lin等[15]所得到的规律:高波陡情况下爬升厚度比低波陡要薄,较薄波舌的能量传递对前侧爬升高度增加的贡献很大,但会导致后侧的上升高度降低基本一致.
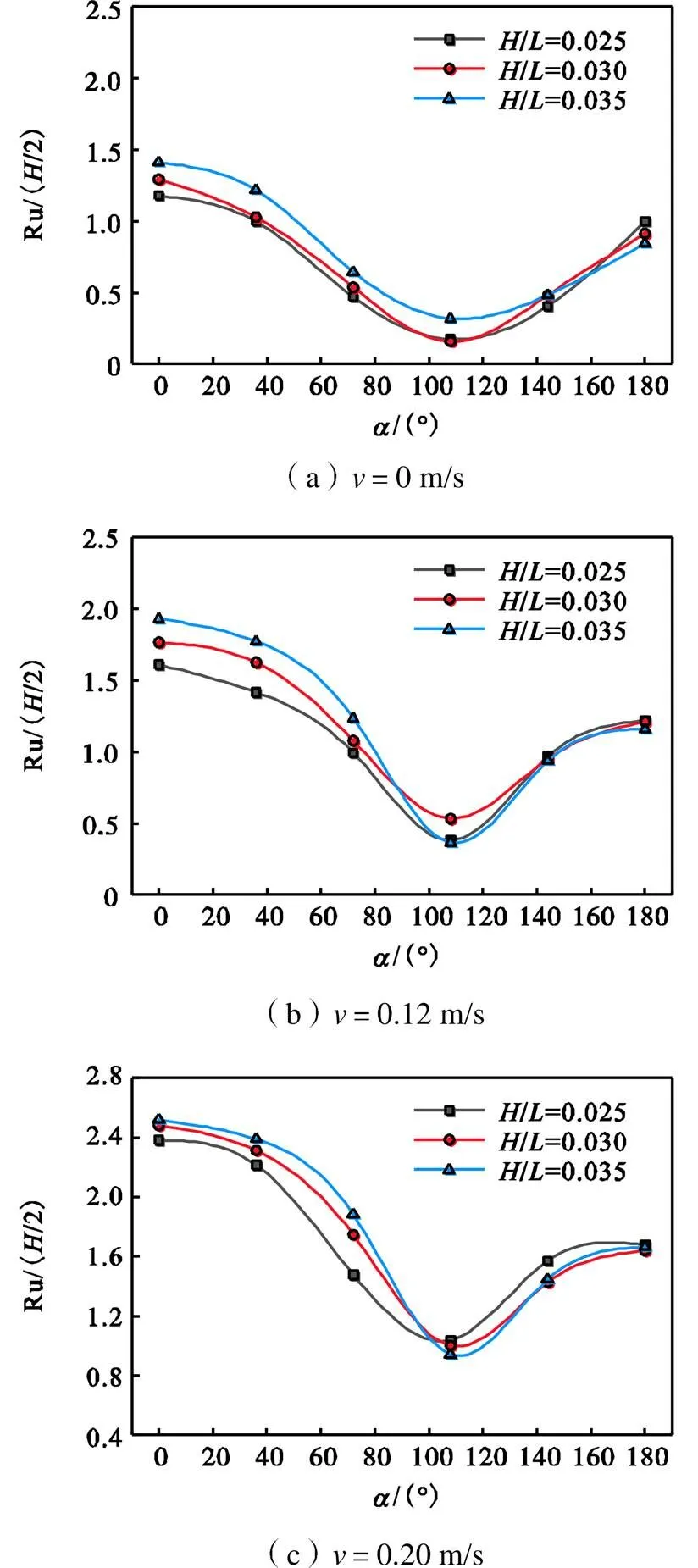
图12 不同波流组合下复合筒型基础反弧段不同周向上波浪爬升的分布规律
图13~16分别给出了A1、C1、E1、F1处波浪爬升时程和相应的频谱图.当波浪和水流沿着复合筒型基础绕射时将会出现以下特征:①对比图13~16可以看出,随着流速比的增大,波浪爬升高度也相应增加,功率谱也相应增大,波浪爬升在复合筒型基础迎浪面正中央(浪高仪A1)处达到最大,此后,由于水体黏性和复合筒型基础的阻碍作用,导致波能不断耗散,波幅呈现出减小的趋势(浪高仪C1至E1的变化)继而因为两侧边波在复合筒型基础背浪面(浪高仪F1处)叠加导致波浪爬升迅速放大;②对比波浪单独作用和波流共同作用时,随着流速比的增大,波浪爬升时程曲线的波峰形状逐渐变尖瘦,从相应的频谱分析中可以发现,流速比越大,所占的非线性成分越多;③浪高仪C1、E1处波面时程曲线发现了对波浪爬升高度的显著高阶贡献,出现二次波峰(如图14、15所示),并且随着流速比增大二次波峰的幅值也相应增大,与图11中的(g)、(i)出现的边波和波面的变形相对应.出现这种现象的原因,可以在 Swan和Sheikh[20]所做的物理试验中找到一些解释,其中波散射的起源与围绕基础的流体循环有关,并且波流共同作用下,二次波峰的出现要早于波浪单独作用.

图13 浪高仪A1处波浪爬升时程和相应的频谱图
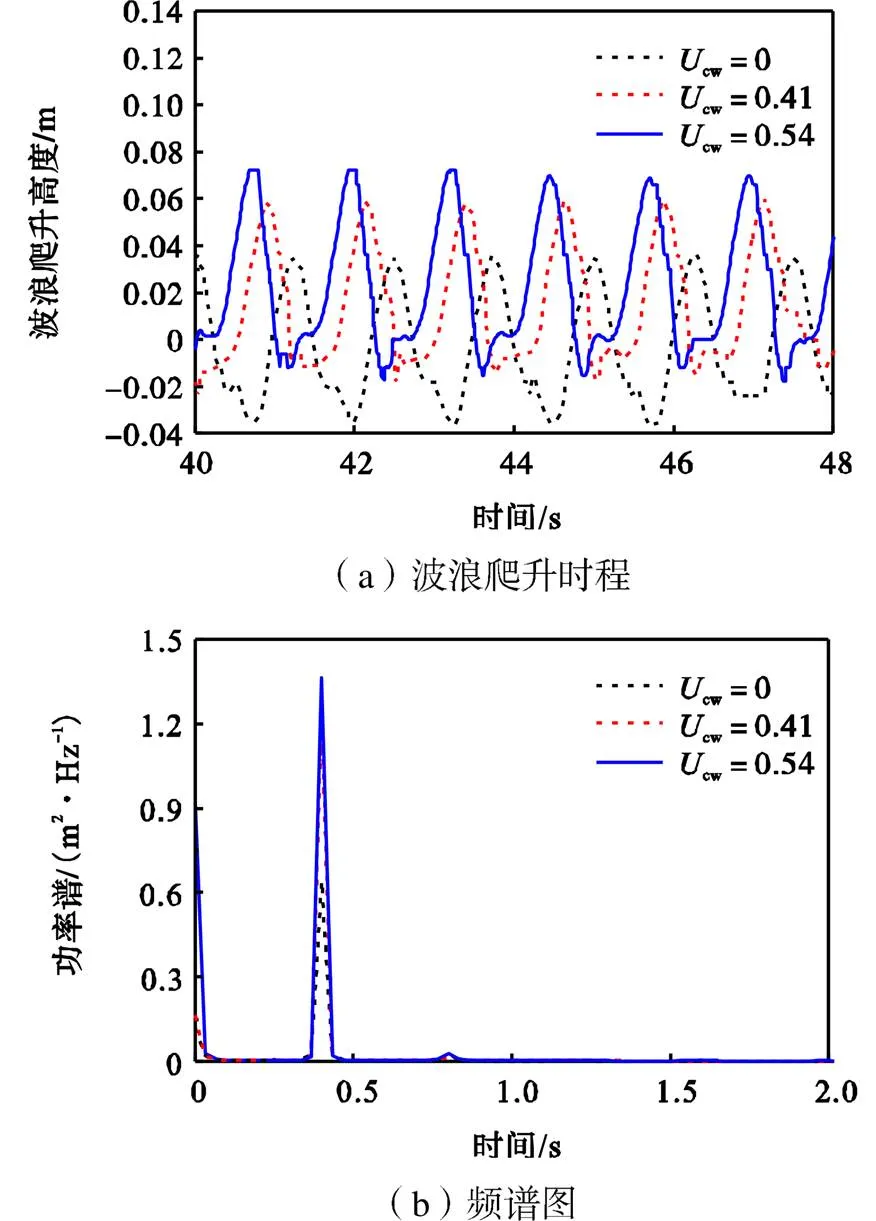
图14 浪高仪C1处波浪爬升时程和相应的频谱图
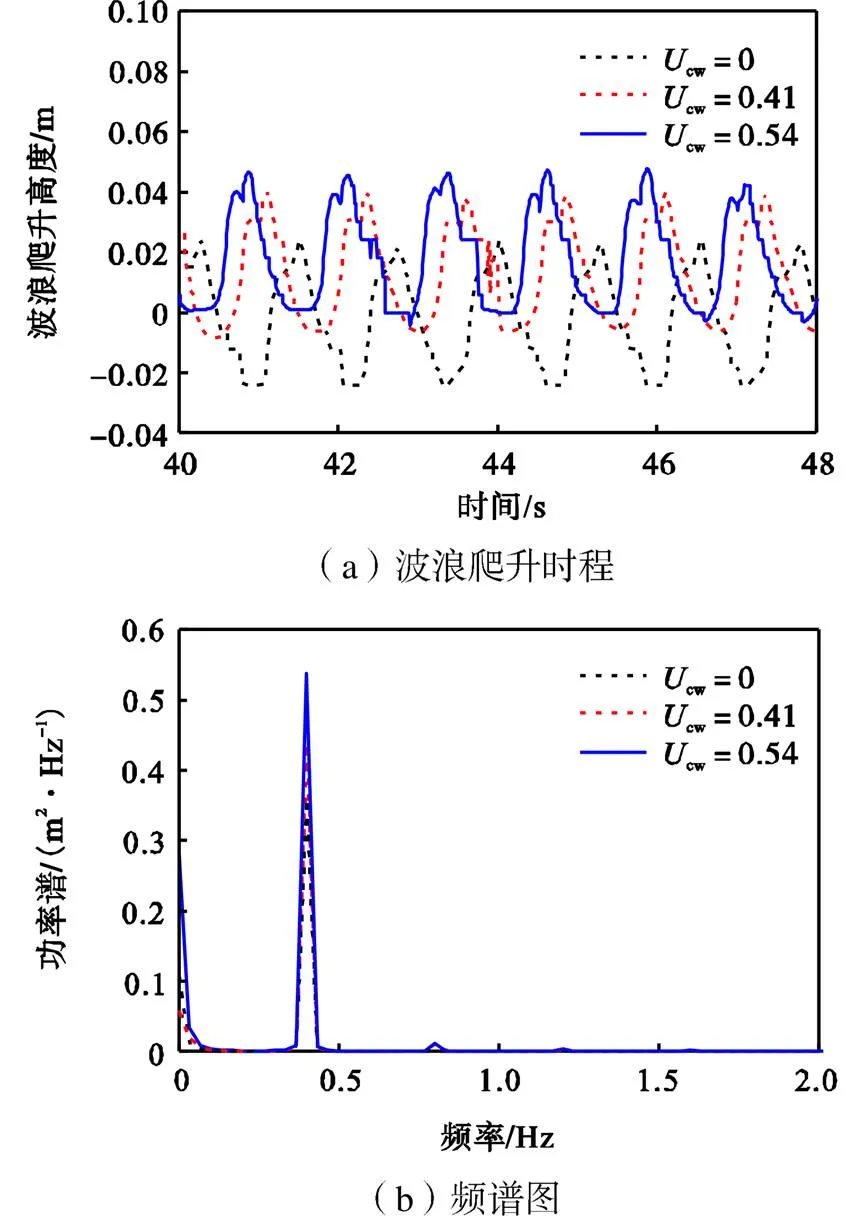
图15 浪高仪E1处波浪爬升时程和相应的频谱图
图17为不同波流组合下复合筒型基础周围各点的爬升分布.其中,为浪高仪至复合筒中心的水平距离,m;为复合筒型基础在其相应水深下对应的水面交界处筒的半径,0.25m水深下=8.07cm.从图中可以得出:①在0°和36°(即A组和B组)方向上各监测点的波浪爬升值随着与基础距离的增大而减小,在D组方向上各监测点的波浪爬升值反而随着与基础距离的增大而增大,这种现象可以用伯努利方程来解释,靠近基础的水质点速度较大,通过自由液面的伯努利方程可知波面高程随着与基础距离的增大而增大.C组、E组和F组方向上波浪爬升值随着与复合筒型基础距离的增大变化不明显.②流速比增大0.28倍,波浪爬升高度增大约0.55倍,这表明增大海流的速度会引起爬升高度的显著增加.
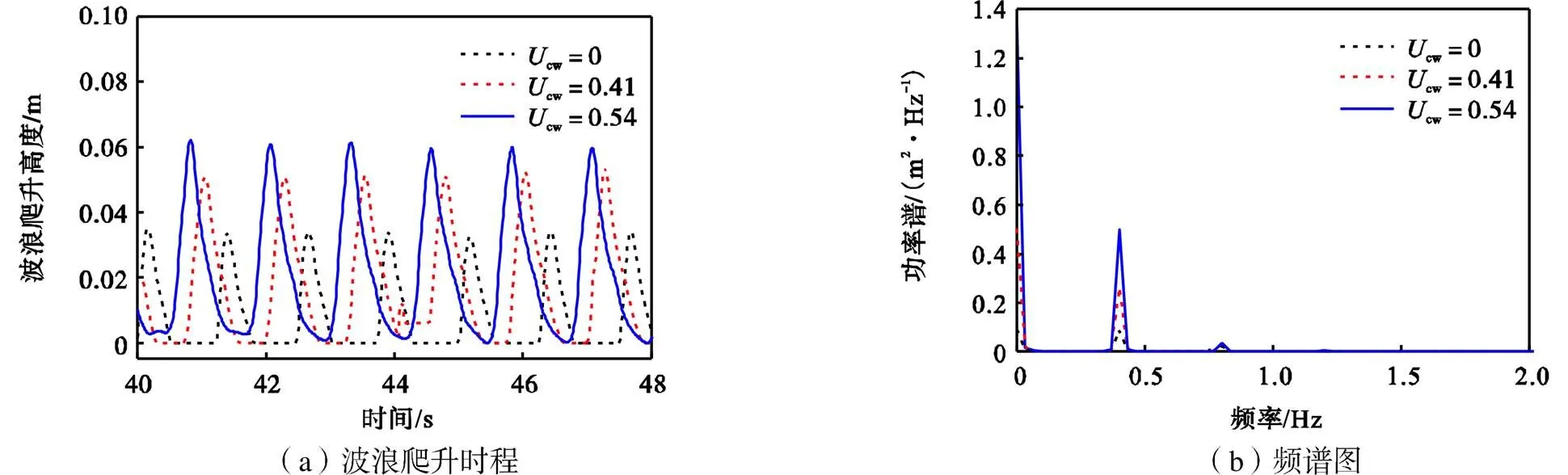
图16 浪高仪F1处波浪爬升时程和相应的频谱图

图17 H/L=0.025时不同波流组合下各个浪高仪组的波浪爬升分布
4 结论
(1) 当复合筒型基础前端波浪回落到波谷位置,波流共同作用时,其前端流体质点朝着多个方向运动,较为紊乱,产生顺时针方向旋转的漩涡;背面水质点沿着不同方向传播,迅速扩散,仅有波浪作用时水质点的方向比较一致.
(2) 波浪单独作用和波流联合作用时,水体回荡过程相似,波浪单独作用时,复合筒型基础背浪面水体呈“公鸡尾”状,而波流联合作用时,复合筒型基础背浪面水体呈“双髻鲨”状;波浪爬升的最大值都出现在复合筒型基础迎浪面正中心即0°(A1)附近,波浪爬升的最小值约在108°(D1).
(3) 对比波浪单独作用和波流共同作用时发现,随着流速比的增大,波浪爬升时程曲线的波峰形状逐渐变尖瘦,从相应的频谱分析中可以发现,随着流速比的增大,非线性成分所占的比例也随之增大.
(4) 复合筒型基础在A组(0°)和B组(36°)时的波浪爬升随着与复合筒型基础距离的变化与在D组(108°)时的波浪爬升变化趋势呈现出相反的规律.而在C组(72°)、E组(144°)和F组(180°)的爬升情况随着与复合筒型基础距离的增大变化并不明显.流速比由0.46增大到0.59时,波浪爬升高度增大约0.55倍.
[1] 王月普. 风力发电现状与发展趋势分析[J]. 电力设备管理,2020(11):21-22.
Wang Yuepu. Analysis of current situation and develop-ment trend of wind power generation[J]. Power Equip-ment Management,2020(11):21-22(in Chinese).
[2] 曲 罡. 海上风电筒型基础结构设计研究[D]. 天津:天津大学,2010.
Qu Gang. The Structural Design Study of Bucket Foundation in Offshore Wind Power[D]. Tianjin:Tianjin University,2010(in Chinese).
[3] Lian Jijian,Ding Hongyan,Zhang Puyang,et al. Design of large-scale prestressing bucket foundation for offshore wind turbines[J]. Transactions of Tianjin University,2012,18(2):79-84.
[4] Liu Meimei,Yang Min,Wang Haijun. Bearing behavior of wide shallow bucket foundation for offshore wind turbines in drained silty sand[J]. Ocean Engineering,2014,82:169-179.
[5] Ding Hongyan,Liu Yonggang,Zhang Puyang,et al. Model tests on the bearing capacity of wide-shallow composite bucket foundations for offshore wind turbines in clay[J]. Ocean Engineering,2015,103:114-122.
[6] Ding Hongyan,Hu Ruiqi,Zhang Puyang,et al. Load bearing behaviors of composite bucket foundations for offshore wind turbines on layered soil under combined loading[J]. Ocean Engineering,2020,198:106997.
[7] 张浦阳,张 志,丁红岩,等. 筒型基础预应力过渡段结构传力特性研究[J]. 太阳能学报,2017,38(11):3144-3150.
Zhang Puyang,Zhang Zhi,Ding Hongyang,et al. Research on force transmission chatacteristics of prestressed transition structure of bucket foundation[J]. Journal of Solar Energy,2017,38(11):3144-3150(in Chinese).
[8] 于通顺,练继建,齐 越,等. 复合筒型风电基础单向流局部冲刷试验研究[J]. 岩土力学,2015,36(4):1015-1020.
Yu Tongshun,Lian Jijian,Qi Yue,et al. Experimental study of the local scour around the composite bucket foundations of wind turbines under unidirectional current[J]. Rock and Soil Mechanics,2015,36(4):1015-1020(in Chinese).
[9] 于通顺,张舒博,章誉天,等. 复合筒基细砂地基波流冲刷过程及最大冲深研究[J]. 太阳能学报,2021,42(8):434-439.
Yu Tongshun,Zhang Shubo,Zhang Yutian,et al. Study on scour process and maximum scour depth of fine sand composite bucket foundation induced by wave and current action[J]. Journal of Solar Energy,2021,42(8):434-439(in Chinese).
[10] Li Jinxuan,Wang Zhanhang,Liu Shuxue. Experimen-tal study of interactions between multi-directional focused wave and vertical circular cylinder,Part I:Wave run-up[J]. Coastal Engineering,2012,64(6):151-160.
[11]单铁兵,杨建民,李 欣,等. 水流对立柱周围波浪爬升特性的影响[J]. 上海交通大学学报,2014,48(1):116-124,131.
Shan Tiebing,Yang Jianmin,Li Xin,et al. Current efforts on wave run-up characteristics around column[J]. Journal of Shanghai Jiao Tong University,2014,48(1):116-124,131(in Chinese).
[12] Bonakdar L,Oumeraci H,Etemad-Shahidi A,et al. Run-up on vertical piles due to regular waves:Small-scale model tests and prediction formulae[J]. Coastal Engineering,2016,118:1-11.
[13] Cheng M H,Hwang R R,Hsieh C M. Numerical study on the transformation of an internal solitary wave propagating across a vertical cylinder[J]. Applied Ocean Research,2020,95:102016.
[14] Cao Hongjian,Wan Decheng. Benchmark computations of wave run-up on single cylinder and four cylinders by naoe-FOAM-SJTU solver[J]. Applied Ocean Research,2017,65:327-337.
[15] Lin Yuhsien,Chen Jingfu,Lu Poying. A CFD model for simulating wave run-ups and wave loads in case of different wind turbine foundations influenced by nonlinear waves[J]. Ocean Engineering,2017,129:428-440.
[16] Lin Y H,Lu P Y,Lin C W,et al. Numerical simulation of maximum wave loads and run-up heights on offshore wind turbine foundations influenced by the instability of bichromatic wave groups[J]. Marine Structures,2019,67:102648.
[17] Yu Tongshun,Zhao Zishuai,Shi Zhongyu,et al. Experimental investigation of wave load and run-up on the composite bucket foundation influenced by regular waves[J]. Journal of Ocean University of China,2021,20(2):271-284.
[18]李玉成. 波流共同作用下的波浪要素[J]. 大连工学院学报,1982(4):81-89.
Li Yucheng. Wave elements under the combined action of wave and current[J]. Journal of the Dalian University of Technology,1982(4):81-89(in Chinese).
[19] Sun L,Zang J,Chen L F,et al. Regular waves onto a truncated circular column:A comparison of experiments and simulations[J]. Applied Ocean Research,2016,59(1):650-662.
[20] Swan C,Sheikh R. The interaction between steep waves and a surface-piercing column[J]. Philos Trans A Math Phys Eng,2015,373(2033):41251-41257.
Numerical Simulation of the Effect of Current on Wave Run-Up Around Composite Bucket Foundation
Yu Tongshun1,Song Haoyang1,Liu Meimei2,Zhang Yutian3
(1. College of Engineering,Ocean University of China,Qingdao 266100,China;2. CCCC Fourth Harbor Engineering Institute Co.,Ltd.,Guangzhou 510230,China;3. Dianjiang CountyWater Conservancy Bureau of Chongqing City,Chongqing 408300,China)
Composite bucket foundation(CBF)is a new type of offshore wind turbine foundation. When wave and current interact with its large-scale arc transition structure,complex wave run-up occurs,which heavily affects the safety of the platforms. Thus,it is necessary to study the wave run-up effect on CBF. First,a numerical wave-current tank was established using the RNG-model. Secondly,the accuracy of the numerical model was verified based on the experimental data. Finally,the law of the wave run-up around the CBF under the action of wave and current was explored,and the contribution of current to wave run-up under different velocity ratioscwwas revealed. The results show that:①Under the action of wave alone,when the water in front of the CBF falls back to the lowest point,the motion trajectory of the water particles is relatively regular,and the vector directions are inclined downward. However,under the combined action of wave and current,a vortex is formed at the front end of the CBF,and the water particles on the back will diffuse in different directions. ②When the wave acts alone,the water on the back of the CBF is a“cock tail”shape,while when the wave and current act together,the water on the back of the CBF is a “hammerhead shark”shape. ③When the wave steepness parameter is 0.025 and the velocity ratio increases from 0.46 to 0.59,the wave run-up height increases about 0.55 times.
composite bucket foundation(CBF);wave run-up;wave-current interaction;numerical simulation
10.11784/tdxbz202110024
TV92
A
0493-2137(2022)12-1309-09
2021-10-26;
2021-12-09.
于通顺(1986— ),男,博士,副教授.
于通顺,tshyu707@ouc.edu.cn.
泰山学者工程专项经费资助项目(ts20190914);国家自然科学基金资助项目(52071304,51509230);山东省重点科研开发项目(2019GHY112044).
Supported by the Special Funds for the Taishan Scholars Project(No.ts20190914),the National Natural Science Foundation of China (No.52071304,No.51509230),the Key Research and Development Program of Shandong Province(No.2019GHY112044).
(责任编辑:樊素英)

