网格强化波折钢板剪力墙滞回性能分析

窦 超，张 晗，杨 潇，杨 娜

网格强化波折钢板剪力墙滞回性能分析

窦 超1, 2，张 晗1，杨 潇1，杨 娜1

(1. 北京交通大学土木建筑工程学院，北京 100044；2. 结构风工程与城市风环境北京市重点实验室，北京 100044)

为了进一步提升钢板剪力墙结构的抗侧性能和抗震能力，提出了一种新型的波折钢板墙形式，即网格强化波折钢板剪力墙．次框架将单片波折墙板分割成若干块小的内嵌墙板，次框架与内嵌墙板协同工作，并与边缘框架形成一个整体抗侧力体系．基于有限元数值分析，建立内嵌墙板分别为单片平钢板、单片波折钢板、网格强化平钢板和网格强化波折钢板的4组不同形式的模型算例，对其在往复加载下的滞回性能进行分析．对比研究了各算例的应力发展、墙板面外变形、滞回曲线和等效阻尼比等结果，并选取关键截面提取边缘框架柱的轴力、剪力和附加弯矩等内力结果进行分析比较．随后，探讨了分块墙板数量、网格数量、各部件钢材强度的变化和肋板刚度比对结构滞回性能、应力发展情况和结构承载力的影响．研究发现，次框架的设置可使钢板剪力墙的滞回曲线更加饱满，改善了单片平墙板滞回曲线的“捏缩”现象和单片波折墙板承载力的退化现象，显著提升了墙板的抗侧性能及耗能能力．大震层间位移角下网格强化波折钢板剪力墙仅发生微弱的面外变形，大幅度改善了传统单片墙板面外变形大、舒适性低的缺点．由于次框架及分块墙板的作用，网格强化钢板墙边缘框架柱的剪力分布更为均匀，由“拉力带”作用产生的边缘框架柱附加弯矩也明显下降．此外，变化关键参数分析表明，减少分块墙板数量可改善波折钢板剪力墙的抗侧承载力退化现象，而次框架网格数减少则会加剧承载力退化问题；边缘框架和次框架采用更高强度钢材使墙板的承载能力和抗震性能得到明显的提高；肋板刚度比的增大能有效提高墙板的抗侧承载效率，设计中应满足最小刚度比要求．总体来看，网格强化波折钢板剪力墙形成了多道抗震防线，合理设计能实现内嵌钢板→次框架→边缘框架的屈服顺序，有效减少了边缘框架的屈服区面积，整体上具有良好的抗侧承载力和耗能能力．

网格强化；波折钢板剪力墙；抗侧性能；滞回性能；框架内力

经过近几十年的大量研究和工程实践，传统平钢板剪力墙体系因其优良的抗震性能已经被工程界认可，形成了相关规程并得到广泛的推广和应用[1-4].近些年来，针对平钢板墙存在的易屈曲、舒适性不足、滞回曲线捏拢等问题，学者提出了波折钢板剪力墙[5-8]，其以波折的形式增加了墙板面外刚度，使其抗侧机制向厚板的剪切屈服机制转变，从而提高了结构抗侧刚度及耗能能力．

目前国内外已开展了系列研究工作．郭彦林等[5-7]提出并研究了多种形式的波折钢板剪力墙，包括单片波折钢板剪力墙、竖向加劲波折钢板剪力墙、平行对扣连接双波折钢板剪力墙和正交对扣连接双波折钢板剪力墙等．窦超等[9-11]通过有限元方法分析了内嵌波折钢板的抗侧力机制，提出相对应的框架柱门槛抗弯刚度要求，研究了竖向荷载对墙板性能的影响，给出墙板的工程优化设计建议．并对波折钢板剪力墙的抗剪性能及屈曲后行为进行了研究，考察了波折钢板剪力墙各个参数对屈曲荷载产生的影响．赵秋红等[12]通过对4种不同类型钢板剪力墙的缩尺模型进行低周往复加载试验发现，波纹钢板剪力墙具有更好的屈曲稳定性和侧向刚度，且深波纹更有利于结构抗震．王威等[13]通过对水平波折和竖向波折钢板剪力墙模型进行低周往复加载试验来研究其力学性能．基于试验结果得出结论，相比较于竖向波折钢板剪力墙，水平波折钢板剪力墙的极限荷载更高、滞回曲线更加饱满．Tong等[14]在研究中提出可以通过增加竖向加劲肋来增大墙板的面外刚度，降低墙板的面外变形，从而提高波折钢板剪力墙的抗侧性能．解程等[15]提出了一种波折板外包平钢板的新型钢板剪力墙，阐述了其构造形式以及工作机理，通过单向推覆分析以及滞回分析，研究了各算例的抗侧性能，发现在大宽高比参数下，组合钢板墙抗侧性能最佳．

上述研究证实了波折钢板剪力墙的优越性能，但也发现了其存在的问题，尤其是当墙板高度及宽度较大，或波折尺寸选取不合适时，单片波折墙板的面外刚度不足，由于“手风琴”效应将导致屈曲或屈服后抗侧承载力迅速下降、延性不足等现象[9-10]．因此在设计中需要对墙板进行优化选型设计[11]．但由于受到波折墙板加工厚度的限制，有些情况下波折墙板很难做到优化选型(例如宽高比过大时)，即仍无法避免上述屈曲后承载力和延性不足的问题[10-11]．此外，大幅面的波折墙板给加工制作、运输安装等均带来了较大的困难[16]．

针对以上问题，本文提出了一种新型波折钢板剪力墙结构，即网格强化波折钢板剪力墙．基于有限元数值方法，建立内嵌墙板分别为单片平钢板、单片波折钢板、网格强化平钢板和网格强化波折钢板的4组典型钢板墙算例，进行低周往复加载，对比其应力变形发展过程、滞回曲线、耗能能力以及边缘框架内力等，明确网格强化波折钢板墙结构的抗侧机理．同时讨论分块墙板数量、网格数量和各部件钢材强度等参数对其抗侧性能的影响，提出相应的工程设计建议．

1 有限元方法验证及算例信息

网格强化波折钢板剪力墙构造形式如图1所示，内嵌墙板分为次框架和被分隔的分块波折钢板两部分．

次框架由横向和纵向的方钢管通过焊接而成，在所形成的网格内部放置分块波折钢板，整块内嵌墙板最终与边缘框架连接．

对于难以进行优化设计的单片波折墙板，其通过设置次框架将大幅面的单块波折墙板分割成若干小墙板，一方面降低了因墙板面积过大带来的加工及运输不便、抗侧性能不佳等问题，另一方面形成的分块墙板其高厚比更小、抗侧及耗能能力更优．此外，次框架不同于之前研究中墙板加劲肋[17-19]，其可以直接参与结构的抗侧，与分块波折钢板协同工作，提高了整体刚度和承载力，同时可形成内嵌钢板→次框架→边缘框架的合理屈服顺序，从而有效地耗散地震能量.

图1 网格强化钢板墙构造

图2 有限元模型

约束顶梁的平面外侧移，在顶梁中心处耦合的参考点施加位移进行低周往复加载，梁底固结，采用静力通用分析法进行模拟．参考我国《高层民用建筑钢结构技术规程》(JGJ99—2015)[20]和美国《钢结构抗震技术规程》(AISC341-10)[21]中对剪力墙体系滞回试验加载制度的相关规定，分级逐渐增加层间位移角，水平加载位移分别为±0.5%、±1.0%、±1.5%、±2.0%，…，最终加载至4.0%的层间侧移角.在低周往复推覆分析之前，选取侧向力作用下的第1阶墙板屈曲模态作为初始缺陷，缺陷幅值为/1000.

为验证有限元方法的有效性与准确性，选取文献[22]中的两层单跨波折钢板墙试件HCoSPSW-Ⅰ，按照上述建模及分析方法模拟试验加载过程．模型如图3(a)所示，边界条件与试验相同，材料参数采用材性试验的结果．从图3(b)可以看到，数值分析结果与试验的滞回曲线较为吻合，尤其是极限承载力基本一致，对加载后期出现的承载力退化情况也能比较精确地跟踪模拟．这说明本文基于ABAQUS的建模和分析方法能够用于波折钢板剪力墙结构的抗侧性能计算．

为了对比不同形式钢板剪力墙的抗侧性能，依据“内嵌墙板＋次框架”与单片墙板用钢量相同的原则，设计了4个典型算例进行分析研究．其中，S-1为普通单片平钢板剪力墙，S-2为单片波折钢板剪力墙，S-3为网格强化平钢板剪力墙，S-4为网格强化波折钢板剪力墙，具体构造见图4．4个模型的边缘框架梁柱均为工字形截面××f×w＝450mm×450mm×15mm×22mm，次框架采用180mm×180mm×5mm标准方钢管，其余具体几何参数见表1．无特殊说明时，边缘框架钢材的屈服强度y＝345MPa，墙板及次框架的屈服强度y＝235MPa，材料本构模型如前文所述．

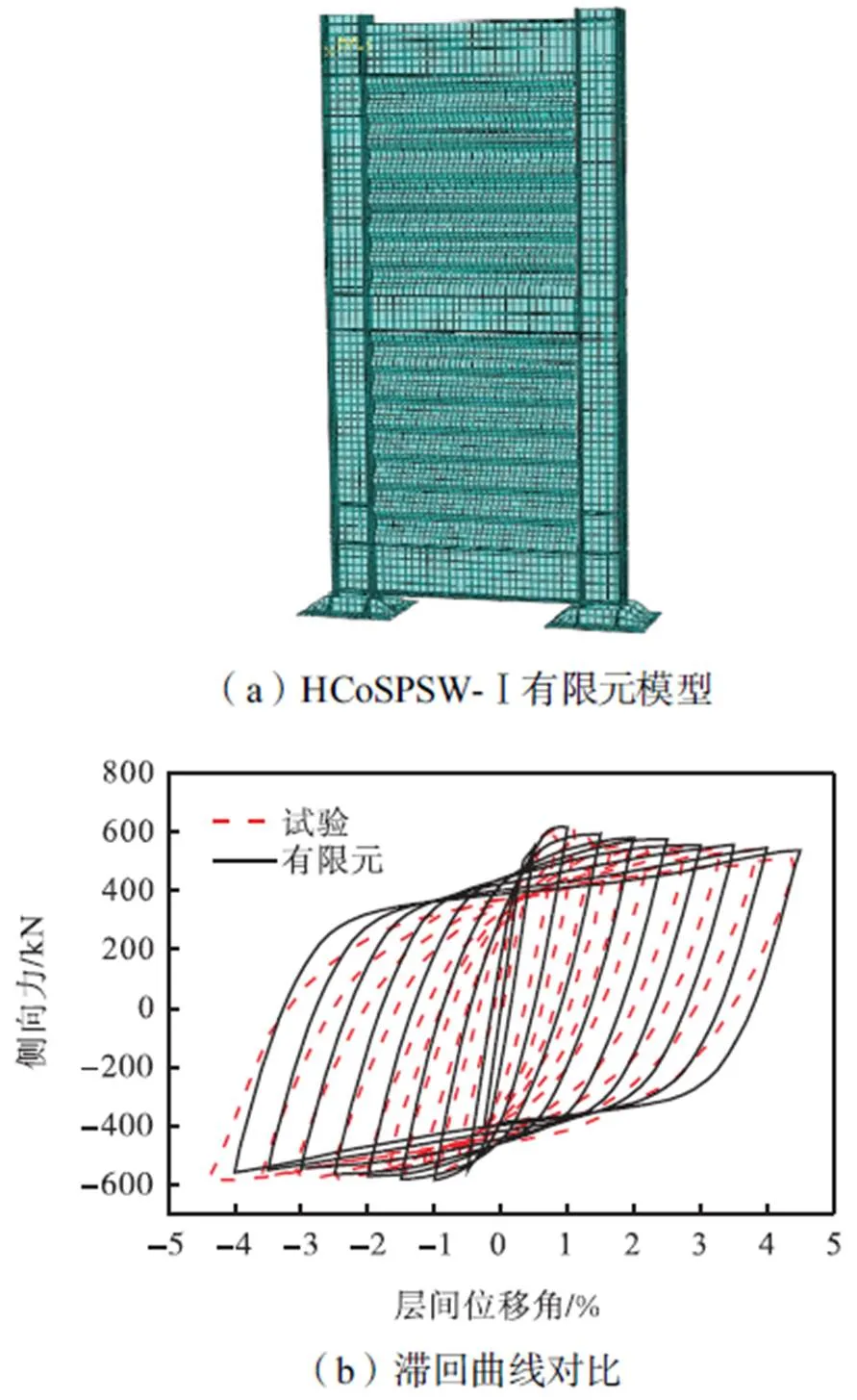
图3 有限元模型验证

值得注意的是，这里的算例S-2并没有特意对波折钢板的尺寸进行优化设计，因此其存在前述不完全拉力带受力及屈曲或屈服后承载力不稳定的问题．从后续结果对比来看，S-4的网格加劲措施确实使此问题得到了改善．

图4 各算例构造形式

表1 S-1～S-4墙板几何参数

Tab.1 Geometric parameters of S-1—S-4

2 应力发展分析

提取4个算例在往复加载的各个层间位移角下的应力云图如图5～图8所示．灰色区域表示应力值超过钢材屈服强度(235MPa、345MPa或下文中的420MPa)．图名中代表层间位移角，下同．

当层间位移角达到0.5%(略大于小震位移限值)时，各算例的内嵌墙板均已出现大面积的屈服，边缘框架梁柱保持弹性．S-1整块平钢板和S-3分块平钢板形成拉力带；不同于S-1和S-3的拉力带机制，S-2的波折钢板墙通过剪切抗侧，波折墙板的屈服区域分布比较均匀；S-4的网格强化波折钢板墙其分块波折墙板呈现整体剪切屈服．

当层间位移角为1.0%时，S-1和S-3的平钢板拉力带进一步发展，墙板屈服区域扩大；S-2的波折墙板屈服面积变化不大；S-4的网格强化内嵌墙板的屈服区域从分块墙板进一步向次框架端部扩展．对于边缘框架，由于拉力带的作用，S-1的一侧框架柱顶和另一侧柱底的整个截面出现了屈服，产生较大范围的塑性变形；S-2的梁柱节点域及柱脚出现了小范围的塑性区；由于S-3和S-4对整片墙板进行了网格加劲，在相应层间位移角下，框架梁柱节点域及柱底的翼缘附近有一定的屈服，但塑性区小于S-1和S-2．

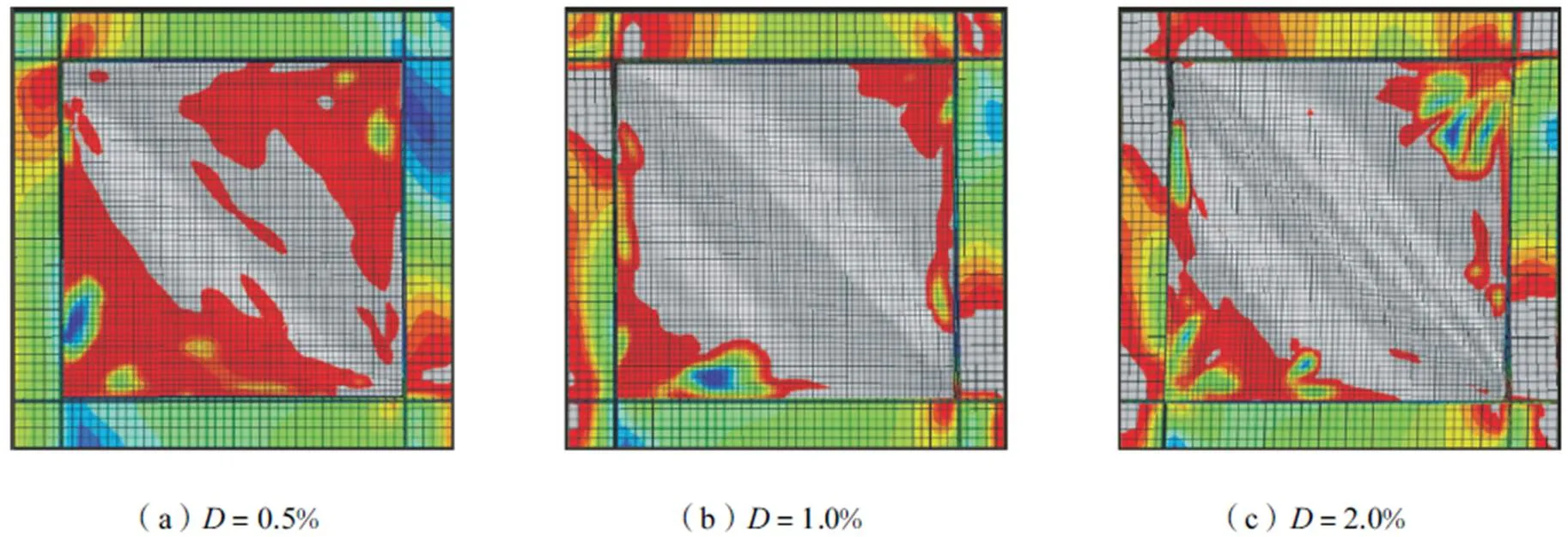
图5 S-1应力发展

图6 S-2应力发展

图7 S-3应力发展

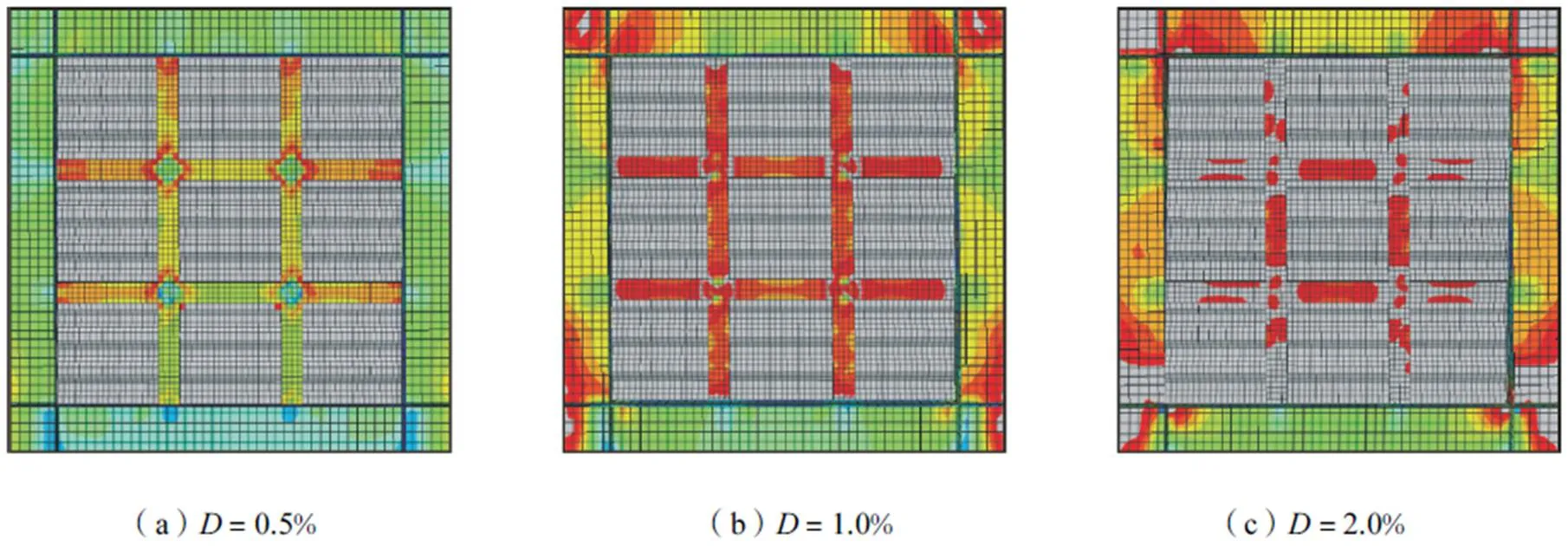
图8 S-4应力发展

随着层间位移角的继续增加，S-1和S-2边缘框架梁柱节点域及框架柱的屈服区域进一步增大，并发展到边缘框架梁端；S-3和S-4的屈服区域则由分块墙板和次框架扩展到边缘框架．整体来看，网格强化钢板剪力墙在大震层间位移角限值(2.0%)下，边缘框架的屈服面积均大幅小于对应的单片钢板剪力墙，且内嵌分块墙板和次框架的塑性发展十分充分，实现结构由内嵌钢板→次框架→边缘框架的屈服顺序．

3 墙板面外变形分析

提取内嵌墙板在往复加载各阶段的最大面外变形结果，绘制成曲线如图9所示．在加载初期(层间位移角为0.5%)，S-1的平钢板很容易失稳产生较大的屈曲变形，而S-2由于波折墙板有较大的面外刚度，其面外变形显著小于S-1的53.1mm．随着层间位移角的增大，S-1的拉力带效应充分发展，平面外变形减缓增长．相比而言，S-2由于内嵌波折墙板屈曲后不完全拉力带的发展及残余变形不断积累，面外变形迅速增长，最终面外变形相当可观．这也从一个侧面说明，未经优化的整片波折墙板其抗侧及延性性能存在较大问题．当然，对于S-3和S-4的网格强化钢板墙，在各级层间位移角下均小于对应的单片钢板墙S-1和S-2，这正是因为次框架的设置将大幅面的单块墙板分割成若干小墙板，极大地降低了分块墙板的高厚比，有效抑制了墙板面外变形．需要的注意的是，S-4在层间位移角达到3.0%前仅发生微小的面外变形，最大仅为13.9mm，但在层间位移角由3.0%增加到3.5%时，由于图9(a)、(b)所示塑性区域的内嵌墙板发生面外失稳，导致最大变形由13.9mm“激增”至120.3mm，超过了同期的S-1和S-3．但总体而言，在大震层间位移角限值(2.0%)之前，网格强化钢板墙尤其是S-4，其面外变形可以得到很好的控制，这对于结构的舒适性及附属结构的使用性均十分有利．

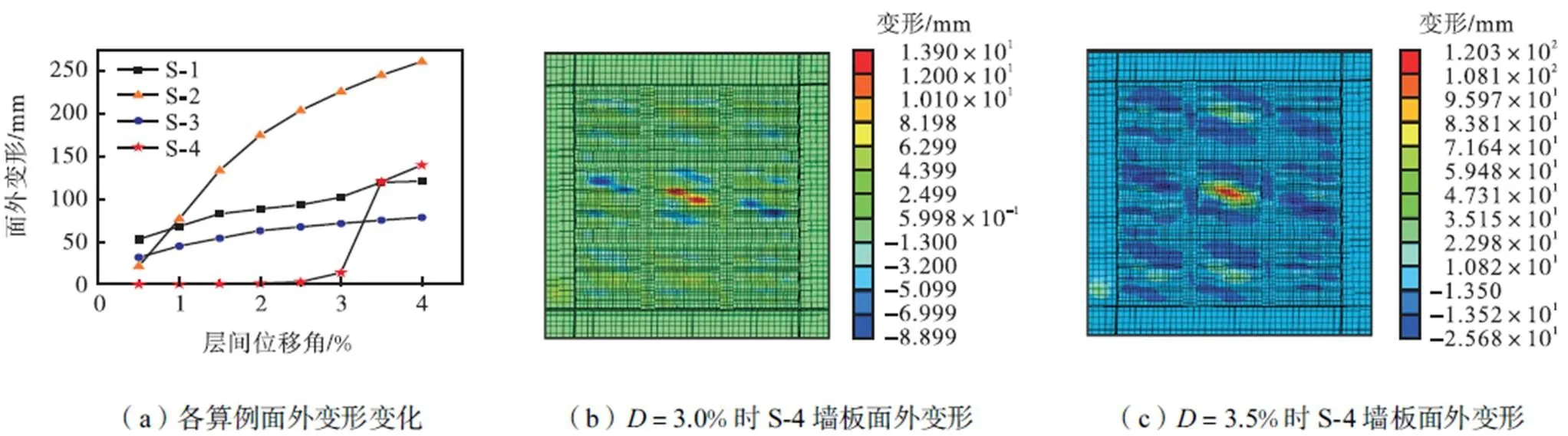
图9 墙板面外变形

4 滞回性能及耗能能力

各算例滞回曲线的结果对比如图10(a)、(b)所示．S-4的滞回曲线最为饱满，体现出优异的抗震性能，而S-1的滞回曲线捏缩严重，削弱了耗能能力；网格强化钢板墙S-3和S-4滞回曲线的饱满程度均高于所对应单片钢板墙S-1和S-2．例如，S-2为未经优化的整块波折墙板，达到极限抗侧承载力后，因面外失稳鼓曲而不能保持面内抗剪继续承载，抗侧能力明显下降．S-4中次框架的设置则有效抑制波折墙板的过大面外变形，保证了其面内剪切屈服的抗侧机制，使承载力退化现象有了较大的改观．需要说明的是，基于“内嵌墙板＋次框架”与单片墙板用钢量相同的原则，相比于S-1的单片平钢板，S-3网格强化平钢板的厚度更小一些；由于次框架的抗侧承载力低于相同用钢量的抗侧墙板，因此S-3承载力相比S-1有一定程度的下降．

为进一步研究各算例的耗能能力，计算得到层间位移角为0.5%～2.0%时整体结构的等效阻尼比，如图10(c)所示．可以看到，各算例的等效阻尼比均随层间位移角的增加而增长，这是由于塑性区的出现和开展使其耗能能力均有不同程度的提高．在同一层间位移角下，S-1的等效阻尼比最小，S-4的等效阻尼比最大，表明其耗能能力优于其他情况．总体来看，波折钢板墙(S-2和S-4)的等效阻尼比均大于所对应的平钢板墙(S-1和S-3)；网格强化钢板墙(S-3和S-4)的等效阻尼比均大于对应的单片钢板墙(S-1和S-2)．由此可见，波折钢板的使用和次框架的设置是提高钢板墙耗能能力的有效措施．

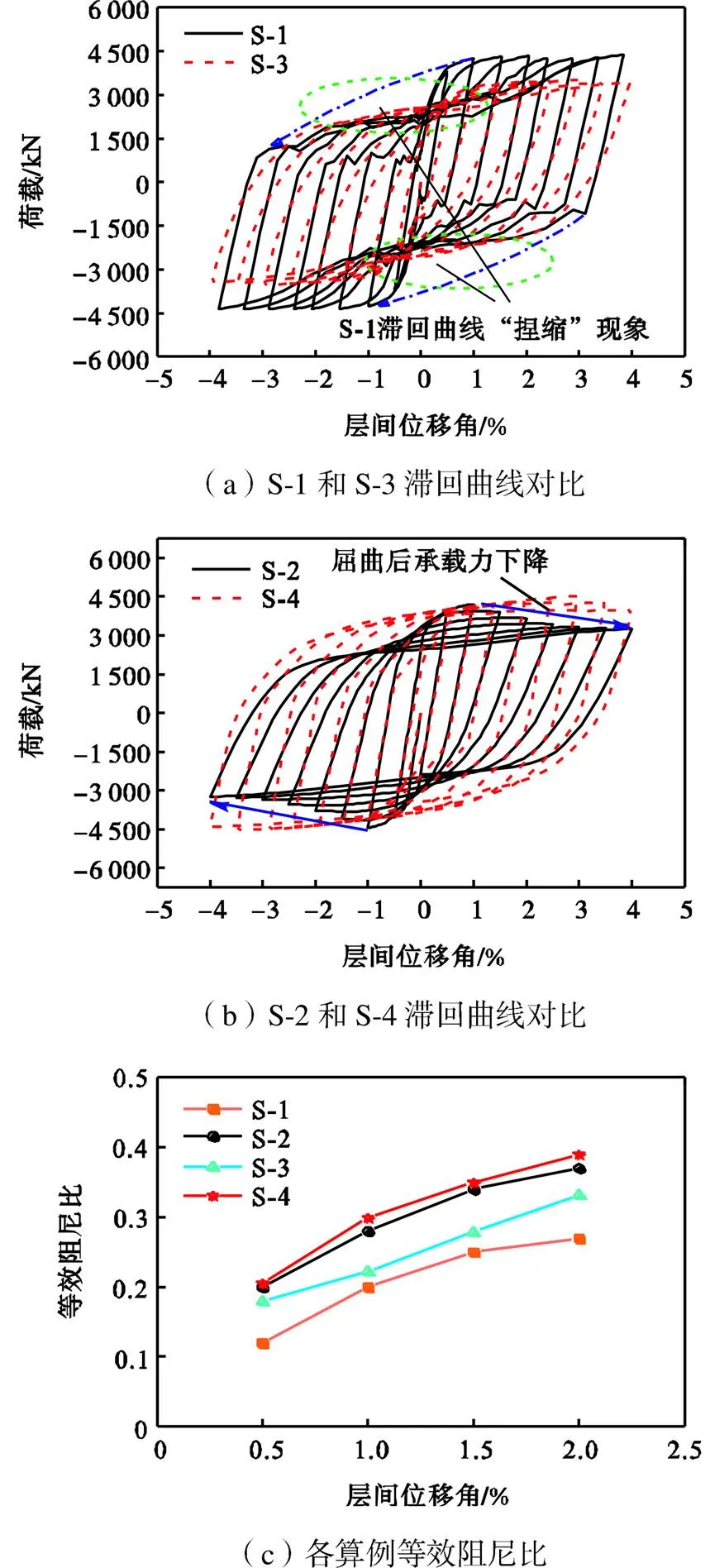
图10 滞回性能对比

5 框架内力分析

在往复加载过程中，边缘框架受到内嵌墙板的拉力带效应或剪切效应而产生附加内力，同时次框架也会在连接部位对边缘框架带来集中作用．这里沿柱高提取0、0.3、0.5、0.7、1.0高度处边缘框架柱截面的轴力和剪力．其中0.3和0.7高度为S-3和S-4中次框架梁和边缘框架柱相交的位置．

由于正向和负向加载时边缘框架柱的内力方向相反、大小大致相等，故只提取正向加载时的内力，并对各内力进行归一化处理．限于篇幅，只给出层间位移角0.5%和2.0%的结果，如图11、图12所示．横坐标为归一化内力，截面屈服内力为

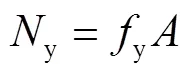
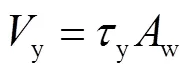
轴力结果表明，S-1和S-3的边缘框架柱轴力存在明显差别．相比S-1，S-3网格强化钢板墙中受压柱的轴压力显著减小，同时受拉柱的轴拉力更大．这样一来叠加上部高层的竖向荷载后，框架柱总体的轴压力减小，受力性能得到改善．

图11 框架柱轴力

图12 框架柱剪力

当层间位移角较小时(0.5%)，S-4中受压柱和受拉柱的轴力量值均比S-2低约20%；当层间位移角较大时(2.0%)，S-4中受压柱和受拉柱的轴力量值均比S-2高约20%．这是由于，在加载初期层间位移角较小时，S-2的内嵌墙板尚未发生显著的面外失稳，因此其以剪切效应为主，受压柱承受着由其倾覆力矩引起的轴压力、墙板剪应力引起的轴力两部分作用．进入加载后期，波折墙板发生面外屈曲，由于局部拉力带的产生，内嵌墙板的剪切效应被削弱，由此导致墙板带给受压柱的轴力部分显著减小，尽管因为抵抗倾覆力矩而产生的轴力部分有所增大，但总轴力幅值仍然降低．

就剪力而言，以受拉柱为例，由于强烈拉力带的作用，S-1的框架柱剪力沿柱高显著变化；当层间位移角比较小时，S-2的框架柱剪力沿高度基本保持不变，但在加载后期由于墙板面外失稳的影响，其剪力变化较大．对于S-3和S-4，由于次框架带来的集中力作用，边缘框架柱剪力曲线在次框架和边缘框架连接位置出现了转折点，但相比S-1和S-2，各截面剪力保持在一定范围内，分布相对均匀，有利于改善框架柱的受力．

为进一步研究板框间的相互作用，建立梁柱铰接剪力墙模型，如图13所示，将边缘框架梁柱设置成无限刚[23-24]，以确保梁柱不参与抗侧，并提取上述截面位置处弯矩，即为内嵌墙板对边缘框架柱产生的附加弯矩．图14为内嵌墙板对边缘框架柱产生的附加弯矩，即不考虑边缘框架自身侧移引起的弯矩，因此曲线的弯曲程度反映了墙板拉力带的影响大小．由图可见，S-1中边缘框架柱的附加弯矩呈显著的曲线分布，表现为强烈的拉力带效应．在加载初期，S-2的整片波折墙板通过剪切抗侧，因此附加弯矩曲线的弯曲程度并不大；随着层间位移角的继续增大，波折墙板屈曲后产生局部拉力带，导致边缘框架柱曲线的显著弯曲．

相比而言，S-3次框架的设置削弱了整片平钢板墙的拉力带效应，在大震层间位移角限值下，弯矩曲线的弯曲程度显著低于S-1和S-2．S-4在波折钢板和次框架的共同作用下，体现了优异的板框相互作用性能，在加载的各阶段框架柱各截面附加弯矩值均为零，并未受到拉力带的影响，墙板实现了高效的剪切抗侧．

图13 铰接框架模型

6 变参数分析

为研究分块墙板数量、网格数量及各部件钢材强度等关键参数对结构抗侧性能的影响规律，保持边缘框架梁柱尺寸、波折墙板和次框架几何参数不变，在算例S-4的基础上，变化关键参数增加3组算例S-5～S-7，其中S-5和S-6的构造如图15所示，比较各算例的应力发展和滞回性能结果．算例的几何参数见表2，其中S-7的构造形式与S-4相同，只是各部件采用不同等级的钢材．值得注意的是，这些算例依据“内嵌墙板＋次框架”与单片墙板用钢量相等的原则，因此S-5和S-6的墙板厚度要大于S-7．

图15 S-5和S-6的构造

这里定义大震层间位移角2.0%所对应的承载力称为残余承载力r，残余承载力系数为r/y，其中y为“墙板＋次框架”全截面剪切屈服承载力．

表2 S-5～S-7墙板几何参数

Tab.2 Geometric parameters of S-5—S-7

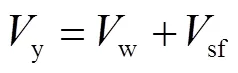
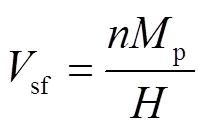
式中：y为材料剪切屈服强度；p为次框架塑性铰弯矩；为次框架屈服时塑性铰个数．

6.1 应力发展

图16～图18给出了S-5～S-7的应力发展情况．可见，各算例均实现多道抗震防线的设计理念，屈服顺序为内嵌钢板→次框架→边缘框架，但具体应力分布与幅值有所不同．S-5在整个加载过程中，中间位置的分块墙板始终未发生屈服，这是由于处于同一层网格或同一跨的另外两块墙板的剪切变形更大，更多地分担了侧向力，而中间墙板受到边缘构件的约束，变形和受力更小．此外，相比较S-4，S-5的边缘框架更早出现较大面积屈服，这是由于相比中间层网格的3块墙板，最上层和最下层网格中只有一块墙板，边缘框架分担的侧向力更大，更早地进入屈服．

对比S-4与S-6发现，网格数量并未显著影响结构整体的屈服顺序，但在大震层间位移角限值下，网格数量的减少导致边缘框架屈服区有一定程度的扩大．此外，S-7与S-4的应力发展情况类似，但次框架和边缘框架梁柱选用了更高强度的钢材，有效地减少了边缘框架的屈服区面积．

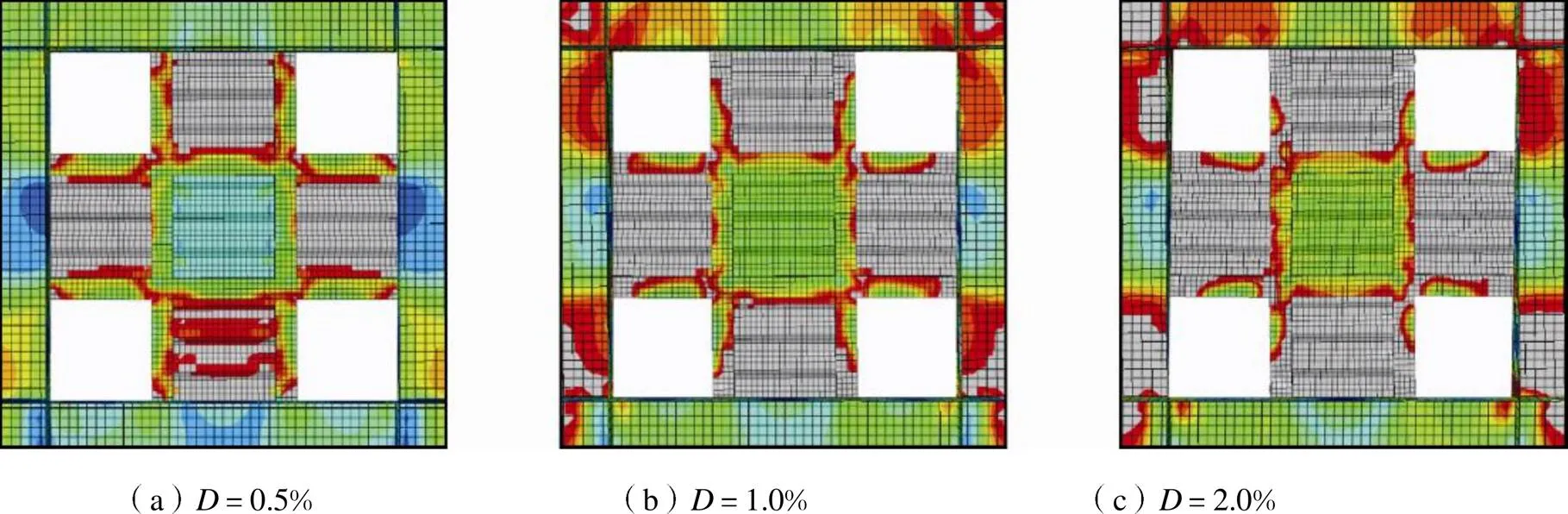
图16 S-5应力发展

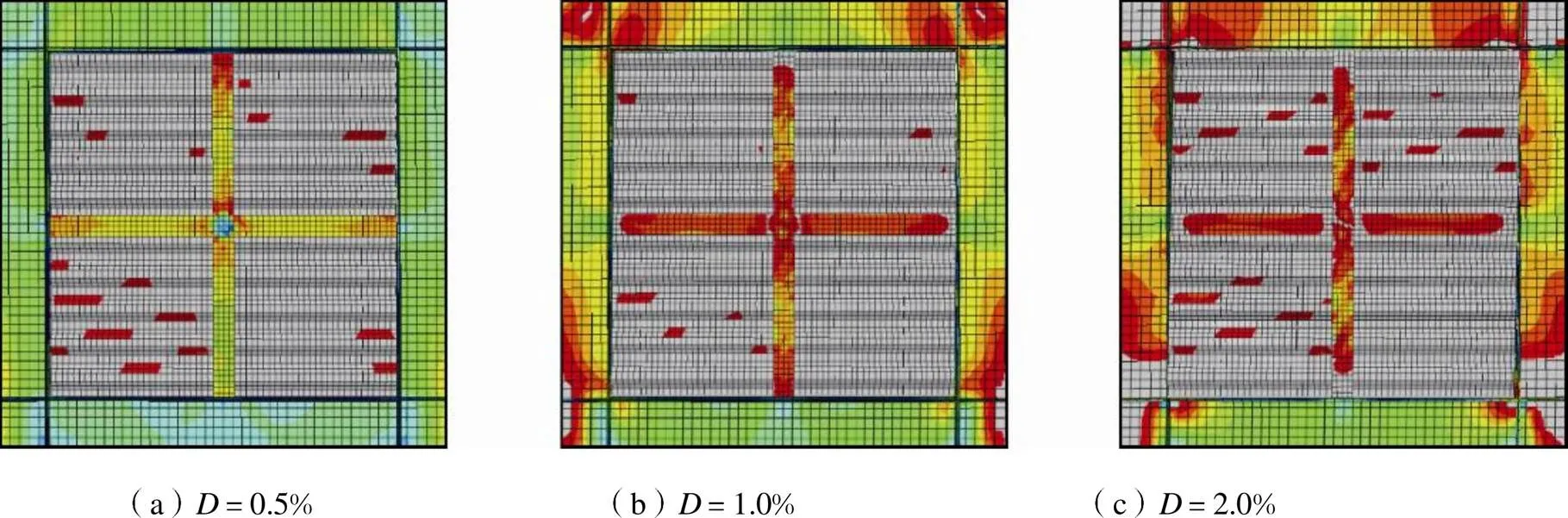
图17 S-6应力发展

图18 S-7应力发展

6.2 滞回曲线

S-5～S-7滞回曲线如图19所示．各算例滞回曲线均较为饱满，体现出良好的滞回性能，其中S-7的滞回曲线最为饱满，承载力最高．通过对比发现，S-5中分块墙板数量减少并没有大幅度降低结构整体的承载能力，反而改善了S-4墙板屈服后承载力下降的现象．S-6由于网格数量的减少，分块波折钢板幅面变大，墙板更易面外屈曲，导致滞回曲线出现了更加明显的承载力下降．S-7的边缘框架和次框架采用更高强度钢材，结构整体的承载力得到了有效提升．

6.3 肋板刚度比

从前述抗侧机理分析可知，次框架的作用之一便是约束限制波折墙板的面外变形，因此设计中应对其面外刚度提出要求．为了反映次框架对内嵌墙板的约束强弱，引入肋板刚度比，为次框架面外抗弯刚度与内嵌墙板刚度之比，即

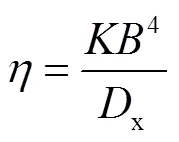
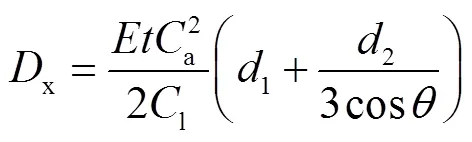
式中：x为墙板的强轴弯曲刚度常数；1为墙板的波峰段宽度；2为墙板的子面板水平宽度；为次框架的面外抗弯刚度；s为网格加劲肋的截面惯性矩；为刚度计算相关系数[25]；为网格数，＝3．

选取典型算例几何参数为＝3.6m，l＝400mm，a/l＝0.10，＝45°．建立梁柱铰接剪力墙模型，如图13所示，采用位移加载进行单向推覆分析直至2.0%．模型共分成3组，分别对应宽高比为1.0、1.5和2.0．每组变换墙板厚度，高厚比设置为1/600、1/450和1/360，来考察不同刚度次框架的加劲效果，最终得出各算例墙板残余承载力系数随肋板刚度比的变化结果如图20所示．

残余承载力系数直接反映了墙板的承载效率，其越接近1.0，表明墙板以面内抗剪屈服机制为主，承载效率高．可以看到，当次框架刚度较小时，墙板的残余承载力系数随着肋板刚度比的增大而迅速提高．当肋板刚度比到达某一限值后墙板残余承载力系数的增速减慢．整体来看，当肋板刚度比≥220时，墙板获得足够的加劲约束，此时各宽高比和高厚比下墙板残余承载力系数均大于0.95，达到充分加劲效果，对应方钢管加劲肋截面尺寸为150mm×150mm×8mm×8mm．因此，规定当墙板的残余承载力系数达到0.95时对应的肋板刚度比为界限肋板刚度比*．以上现象说明次框架面外刚度的提高在一定程度上可以提升墙板的承载效率；而当肋板刚度比到达一定值后，继续增加次框架面外刚度，则对内嵌墙板本身的承载力提升影响不大．另外，对于波折横放的墙板，次框架的设置对大宽高比墙板受力性能的改善更为明显．

定义波折墙板的正则化高厚比[10,14]为

式中y、cr分别为波折墙板的屈服剪力和剪切屈曲荷载．

进一步分析发现，波折墙板的界限肋板刚度比*与墙板正则化高厚比显著相关，将以上两个参数进行拟合，得到界限肋板刚度比*的拟合计算公式为

式(12)的计算结果与有限元数值结果对比如图21所示，二者吻合较好．可以看到，正则化高厚比越小，波折墙板越不易发生面外失稳[9-11]，因此其所需界限肋板刚度比自然随之降低．

图20 残余承载力系数随肋板刚度比的变化

Fig.20 Residual bearing capacity factor along with the rib stiffness ratio

图21 次框架的界限肋板刚度比结果

7 结论

本文提出一种新型的波折钢板墙形式，即网格强化波折钢板剪力墙，选取典型算例，与普通单片平钢板剪力墙、单片波折钢板剪力墙、网格强化平钢板剪力墙的滞回性能进行对比，讨论了分块墙板数量、网格数量和钢材强度的影响规律．

(1) 通过算例的应力发展结果对比发现，网格强化波折钢板剪力墙能够形成多道抗震防线，实现内嵌钢板→次框架→边缘框架的屈服顺序，同时有效减少了边缘框架的屈服区面积．相比普通钢板墙，其滞回曲线最为饱满，等效阻尼比值最大，具有良好的抗侧性能和耗能能力，改善了平钢板剪力墙滞回曲线的捏缩现象以及波折钢板剪力墙后期承载力退化问题．

(2) 网格强化波折钢板剪力墙在大震作用下墙板仅发生微小的面外变形，极大改善了普通钢板墙结构中墙板面外变形过大、舒适性不足的问题．

(3) 网格强化波折钢板剪力墙通过设置次框架降低了墙板对边缘框架柱的附加剪力和弯矩作用，改善了边缘框架的受力．

(4) 减少分块墙板数量可改善波折钢板剪力墙的抗侧承载力退化现象，而网格数量的减少会加剧承载力退化问题；边缘框架和次框架采用更高强度的钢材可有效提升整体承载力和抗震性能．因此，设计中在波折墙板本身优化的基础上，建议选择合适的墙板分块数和网格数、框架选用高强钢材以获得更为优越的结构性能．

(5) 对于网格强化波折钢板墙，随着肋板刚度比的增加，内嵌墙板的抗侧承载性能显著提升．本文给出的界限肋板刚度比拟合公式能够准确反映次框架的约束作用，为设计提供重要参考．

(6) 内嵌波折墙板性能、网格数、分块墙板布置、次框架面外约束刚度与面内抗侧性能等参数是影响网格强化波折钢板剪力墙的重要因素．后续将深入各参数影响进行系统定量化研究，提出相应设计方法和建议．

［1］ 徐 建，石永久，戴国欣，等. 非加劲钢板剪力墙受力性能与设计方法研究进展[C]// 第十一届全国现代结构工程学术研讨会. 天津，中国，2011：324-331.

Xu Jian，Shi Yongjiu，Dai Guoxin，et al. Research progress on mechanical behavior and design method of non-stiffened steel plate shear wall[C]//11th National Symposium on Modern Structural Engineering. Tianjin，China，2011：324-331(in Chinese).

［2］ 蔡克铨，林盈成，林志翰. 钢板剪力墙抗震行为与设计[J]. 建筑钢结构进展，2007，9(5)：19-25.

Cai Kequan，Lin Yingcheng，Lin Zhihan. Seismic responses and design of steel plate shear wall[J]. Progress in Steel Building Structures，2007，9(5)：19-25(in Chinese).

［3］ 刘 伟，王 超. 钢板剪力墙的研究与进展[J]. 吉林建筑大学学报，2017，34(3)：26-30.

Liu Wei，Wang Chao. Research and development of steel plate shear wall[J]. Journal of Jilin Jianzhu University，2017，34(3)：26-30(in Chinese).

［4］ 马欣伯，张素梅，郭兰慧. 两边连接钢板剪力墙试验与理论分析[J]. 天津大学学报，2010，43(8)：697-704.

Ma Xinbo，Zhang Sumei，Guo Lanhui. Theoretical analysis and experiment on steel plate shear wall with two-side connections[J]. Journal of Tianjin University，2010，43(8)：697-704(in Chinese).

［5］ 郭彦林，董全利. 钢板剪力墙的发展与研究现状[J]. 钢结构，2005(1)：1-6.

Guo Yanlin，Dong Quanli. Research and application of steel plate wall in high-rise buildings[J]. Steel Construction，2005(1)：1-6(in Chinese).

［6］ 郭彦林，周 明. 钢板剪力墙的分类及性能[J]. 建筑科学与工程学报，2009，26(3)：1-13.

Guo Yanlin，Zhou Ming. Categorization and performance of steel plate shear wall[J]. Journal of Architecture and Civil Engineering，2009，26(3)：1-13(in Chinese).

［7］ 郭彦林，朱靖申. 剪力墙的型式、设计理论研究进展[J]. 工程力学，2020，37(6)：19-33.

Guo Yanlin，Zhu Jingshen. Research progress of shear walls：Types and design methods[J]. Engineering Mechanics，2020，37(6)：19-33(in Chinese).

［8］ Berman J W，Bruneau M. Experimental investigation of light-gauge steel plate shear walls[J]. Journal of Structural Engineering，2005，131(2)：259-267.

［9］ 窦 超，朱仰泽，解 程，等. 波折钢板剪力墙内嵌墙板与框架的相互作用分析[J]. 钢结构(中英文)，2020，35(12)：22-28.

Dou Chao，Zhu Yangze，Xie Cheng，et al. Analysis of interaction between infill plate and frame in steel corrugated shear walls[J]. Steel Construction(Chinese & English)，2020，35(12)：22-28(in Chinese).

［10］ Dou Chao，Pi Yonglin，Gao Wei. Shear resistance and post-buckling behavior of corrugated panels in steel plate shear walls[J]. Thin Wall Structures，2018，131(1)：816-826.

［11］ Dou Chao，Xie Cheng，Zhao Yuanyuan，et al. Shear resistance and design of infill panels in corrugated plate shear walls[J]. Journal of Structural Engineering，2021，147(11)：04021179.

［12］ 赵秋红，邱 静，李 楠，等. 梯形波纹钢板剪力墙抗震性能试验研究[J]. 建筑结构学报，2018，39(增2)：112-120.

Zhao Qiuhong，Qiu Jing，Li Nan，et al. Experimental study on seismic performance of trapezoidally corrugated steel plate shear walls[J]. Journal of Building Structures，2018，39(Suppl 2)：112-120(in Chinese).

［13］ 王威，张龙旭，苏三庆，等. 波形钢板剪力墙抗震性能试验研究[J]. 建筑结构学报，2018，39(5)：36-44.

Wang Wei，Zhang Longxu，Su Sanqing，et al. Experimental research on seismic behavior of corrugated steel plate shear wall[J]. Journal of Building Structures，2018，39(5)：36-44(in Chinese).

［14］ Tong Jingzhong，Guo Yanlin. Shear resistance of stiffened steel corrugated shear walls[J]. Thin Walled Structures，2018，127：76-89.

［15］ 解 程，窦 超，杨 潇，等. 一种新型组合钢板剪力墙的适用性研究[C]//第二十一届全国现代结构工程学术研讨会. 石家庄，中国，2021：273-278.

Xie Cheng，Dou Chao，Yang Xiao，et al. Applicability study of a new composite steel shear wall[C]//21st National Symposium on Modern Structural Engineering. Shijiazhuang，China，2021：273-278(in Chinese).

［16］ 赵秋红，邱 静，郝博超，等. 两边连接竖向波纹钢板剪力墙的抗侧性能[J]. 天津大学学报(自然科学与工程技术版)，2019，52(增2)：46-53.

Zhao Qiuhong，Qiu Jing，Hao Bochao，et al. Lateral behavior of vertically-corrugated steel plate shear walls connected with beams only[J]. Journal of Tianjin University(Science and Technology)，2019，52(Suppl2)：46-53(in Chinese).

［17］ 杨雨青，牟在根. 不同形式的槽钢加劲钢板剪力墙滞回性能研究[J]. 天津大学学报(自然科学与工程技术版)，2019，52(8)：876-888.

Yang Yuqing，Mu Zaigen. Hysteretic behavior of different forms of channel-stiffened steel plate shear walls[J]. Journal of Tianjin University(Science and Technol-ogy)，2019，52 (8)：876-888(in Chinese).

［18］ 牟在根，张福建，李黎明. 两边连接竖向加劲式钢板剪力墙简化模型[J]. 天津大学学报(自然科学与工程技术版)，2014，47(增)：30-36.

Mu Zaigen，Zhang Fujian，Li Liming. Simplified model for two-side constraint steel plate shear wall (SPSW)with vertical stiffeners[J]. Journal of Tianjin University(Science and Technology)，2014，47(Suppl)：30-36(in Chinese).

［19］ 陈国栋，郭彦林，范珍，等. 钢板剪力墙低周反复荷载试验研究[J]. 建筑结构学报，2004，25(2)：19-26，38.

Chen Guodong，Guo Yanlin，Fan Zhen，et al. Cyclic test of steel plate shear walls[J]. Journal of Building Structures，2004，25(2)：19-26，38(in Chinese).

［20］ JGJ 99—2015 高层民用建筑钢结构技术规程[S]. 北京：中国建筑工业出版社，2015.

JGJ 99—2015 Technical Specification for Steel Structure of High-Rise Civil Buildings[S]. Beijing：China Construction Industry Press，2015(in Chinese).

［21］ AISC 341-10 Seismic Provisions for Structural Steel Buildings[S]. Chicago：American Instutute of Steel Construction，2010.

［22］ Qiu J，Zhao Q H，Yu C，et al. Experimental studies on cyclic behavior of corrugated steel plate shear walls[J]. Journal of Structural Engineering，2018，144(11)：04018200.

［23］ Zhang Xuqiao，Guo Yanlin. Behavior of steel plate shear walls with pre-compression from adjacent frame columns[J]. Thin Walled Structures，2014，77：17-25.

［24］ 窦 超，朱仰泽，解 程，等. 梯形波折钢板剪力墙内嵌墙板抗侧性能研究[J]. 天津大学学报(自然科学与工程技术版)，2021，54(9)：982-990.

Dou Chao，Zhu Yangze，Xie Cheng，et al. Lateral resistance behavior analysis of shear panels in trapezoidal corrugated steel shear walls[J]. Journal of Tianjin University(Science and Technology)，2021，54(9)：982-990(in Chinese).

［25］ 包福廷. 井字梁结构静力计算手册[M]. 北京：中国建筑工业出版社，1989.

Bao Futing. Manual for Static Calculation of Well Beam Structure[M]. Beijing：China Construction Industry Press，1989(in Chinese).

Hysteretic Behavior of a Grid-Reinforced Corrugated Steel Plate Shear Wall

Dou Chao1, 2，Zhang Han1，Yang Xiao1，Yang Na1

(1. School of Civil Engineering，Beijing Jiaotong University，Beijing 100044，China；2. Beijing’s Key Laboratory of Structural Wind Engineering and Urban Wind Environment，Beijing 100044，China)

To further improve the lateral performance and seismic capacity of steel plate shear walls(SPSWs)，a new type of grid-reinforced corrugated steel plate shear walls(CSPSWs)is proposed in this paper. The entire corrugated wall panel is divided into several small wall panels embedded within the subframe，while subframes work together with the embedded wall panel，forming an overall lateral resistance system with the boundary frame. Based on the finite element numerical analysis，four shear wall models，namely，conventional flat SPSW，conventional CSPSW，grid-reinforced flat SPSW，and grid-reinforced CSPSW，are established to analyze the hysteretic performance under cyclic loading. Then，their stress development，out-of-plane deformation，hysteretic curves，and equivalent damping ratios are compared. Meanwhile，the internal forces of the boundary frame columns，namely，axial force，shear force，and bending moment，of the four models are compared. Lastly，the effects of key parameters，such as the number of embedded wall panels and grids and the material strength of different parts and rib stiffness ratio，on the hysteretic performance，stress development，and bearing capacity of the structure are discussed. The results show that the subframe improves the hysteretic performance，including the lateral strength，ductility，and energy dissipation of SPSWs，by reducing the pinch of the hysteretic curve of the conventional flat SPSW and the degradation of the lateral resistance of the conventional CSPSW. In addition，under the maximum story drift ratio，an insignificant out-of-plane deformation occurs in the grid-reinforced CSPSW，which improves the comfortability for common use. Moreover，due to the action of subframes and embedded wall panels，the shear distribution of the boundary frame columns of grid-reinforced SPSWs and CSPSWs is uniform，and the additional bending moment caused by the “tension field” is also significantly reduced. Decreasing the number of embedded wall panels and increasing the number of subframe grids can reduce the degradation of the lateral resistant capacity of the CSPSW. When high-strength steel is used in the boundary frame and subframe，the bearing capacity and seismic performance of the system can be significantly improved. With the increase in the rib stiffness ratio，the bearing capacity of the wall plate is effectively enhanced，and the threshold rib stiffness ratio should be satisfied in the design. Overall，grid-reinforced CSPSWs can yield a reasonable yield order from the embedded steel plate to the subframe and then to the boundary frame and effectively reduce the area of the yield zone of the boundary frame，leading to a good lateral resistance and energy dissipation ability.

grid strengthening；corrugated steel plate shear wall；side resistance；hysteretic behavior；internal force of frame

10.11784/tdxbz202110019

TU391

A

0493-2137(2022)12-1275-14

2021-10-22；

2022-02-04.

窦 超（1984—  ），男，博士，副教授，douchao@bjtu.edu.cn.

张 晗，20125944@bjtu.edu.cn.

国家自然科学基金资助项目(51808032)；中央高校基本科研业务费资助项目(2020JBM041)．

Supported by the National Natural Science Foundation of China(No.51808032)，the Fundamental Research Funds for the Central University (No.2020JBM041).

(责任编辑：金顺爱)