压力传感器温度补偿与实现研究
梁荫娟
(佛山市顺德区质量技术监督检测所,广东佛山 528000)
硅压阻式压力传感器具有测量精度高、动态响应快速且灵敏度高等性能优势,但在注塑模具、空压机、空调制冷、液压系统等众多领域应用期间,压力传感器因其材料自身性质导致非线性、温度漂移等问题难以规避,对测量精度造成较大影响。压力传感器实际工作电流为四个等值薄膜电阻构建的惠斯通电桥,当弹性敏感元件承接被测压力时,将形成与压力成正比的位移量,但受限于生产工艺,导致压力传感器内部电桥无法保持一致性,因此需要采取一定措施对温度进行补偿。
1 压力传感器的工作原理
压力传感器原理为惠斯通电桥,R1~R4四个电阻阻值相同,相互连接构成惠斯通电桥,电桥中的负应力区为R2与R4,正应力区为R1与R3,在膜片承接外界压力的情况下,前者电阻降低,后者电阻增加,由此产生输出为:

其中,R1~R4为电阻,VB为电桥供电电压,VO为电桥输出电压。
当正应力电阻乘积与负应力电阻乘积相等(R1R3=R2R4)时,输出数值为0,两侧存在的压力差将导致膜片出现变形,此时的R2与R4将降低,R1与R3将增加,电桥失去平衡后输出为:

如果压力传感器的四个电阻相等,电阻变化偏差均为ΔR,则此时:

即外界压力与输出数值两者成正比。
2 压力传感器温度漂移的常用补偿方法
压力传感器具有硬件与软件两种补偿方式。其中,硬件补偿需要对压力传感器电路参数与制作工艺进行优化调整,针对零点漂移问题可以采用自平衡电桥、双电桥等方式进行补偿;针对灵敏度漂移问题可以采用二极管、自平衡电桥等方式进行处理[1]。对于已经生产出来的压力传感器,通常难以通过硬件补偿的方式进行处理,此时可以采取软件补偿法,常用的方法主要有数值分析法与人工智能法。本文主要研究了基于数值分析的压力传感器温度补偿方法,该方法常用的算法为最小二乘法与插值法,针对最小二乘法多次拟合存在病态问题但实施难度低以及插值法补偿精度高但实施难度高的情况[2],本文选择将两者算法融合应用,更高效地解决压力传感器温度漂移问题。
3 压力传感器标定试验及分析
在常温环境下,压传感器量程为-40 kPa~40 kPa,按照步长4 kPa 划分压力数值可以得到-40、-36、-32、…、36、40 等21 个压力数值;测试过程中选择在-40℃~80℃范围内控制温度进行变化,得到不同的压力数值。在实际测试过程中,选择将压力传感器的压力与温度测量数值进行A/D 转换和分析,通过EEPROM 可编程存储器内部算法进行分析和补偿,得到补偿后的数值结果并以数字量的形式显示出来[3]。
本文选择将-40℃~80℃的温度划分为13 个温度等级,步长取10℃,通过后续测试可以发现,相对20℃室温而言,在压力等级相同的情况下,压力传感器的测量误差将随着温度与室温差距的增加而增加。
4 压力传感器温度补偿模型
三次样条曲线包括三段曲线,曲线连接点为存在二级连续导数,从而区别三段曲线连接部位的光滑过渡,对于满足压力传感器温度补偿具有重要意义[4]。假设f(x)为[a,b]区间的可微函数,该函数二次连续,在上述区间数量为n+1 的插值节点,且各插值节点数值递增,即a=x1<x2<…<xn<xn+1=b。提出函数:
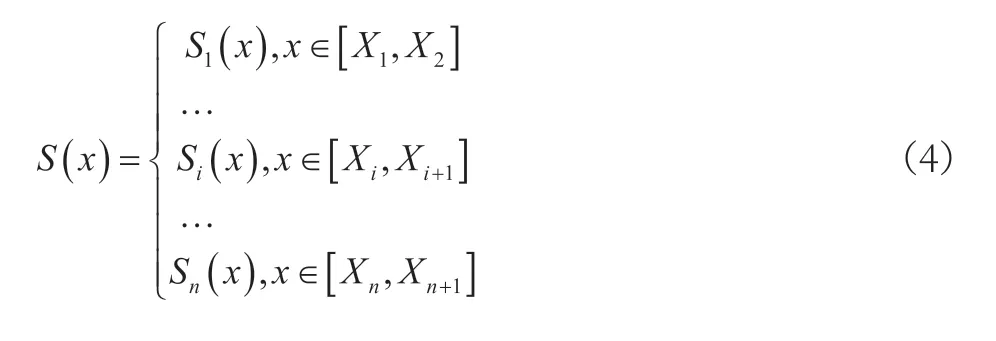
S(x)函数之中,各小区间之间连续且二阶可导;最高次幂均不大于3 且i的数值为[1,n+1],n为正整数;f(xj)=S(xj)且j的数值为[1,n+1],则f(x)的三次样条插值函数即为S(x)。
本文构建的温度补偿模型之中,环境温度与输入压力是影响输出结果的变量,为避免变量影响测量精度,模型建立过程中应该通过标定测试的方式检测相关数值,输出压力F、输入温度t以及输入压力p三者函数关系为F=f(p,t),但实际检测期间需要结合温度与输出压力对输入压力进行反算,则输入压力p’=f-1(F,t)。
首先需要确保n个标定温度点温度数值tj维持不变,将m个压力点pi选作样条插值节点,通过三次样条插值的方法将区间划分为m-1 个,得到输出压力F与输入压力pj之间的m-1段三次样条函数如下:
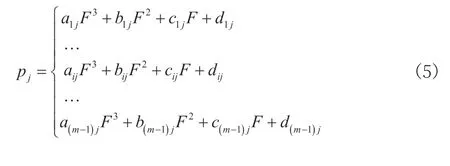
其中,a、b、c、d为各阶函数系数,i为行数,j为列数。
则各分段三次样条多项式对于项系数矩阵为:
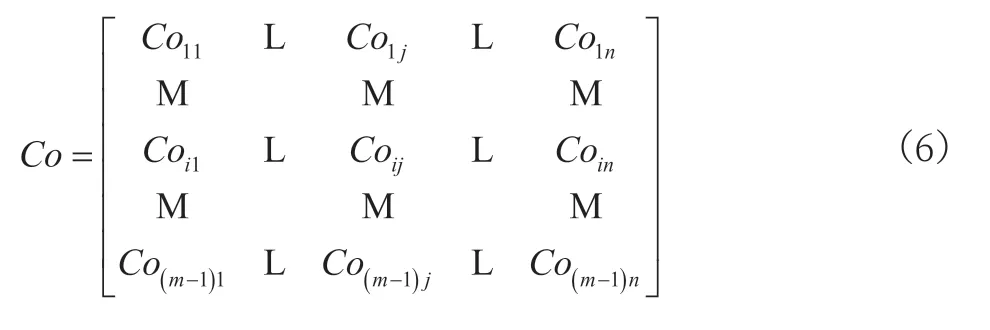
将Co矩阵中的o利用a、b、c、d替换,则可以得到相应的系数矩阵;根据温度数值tj的不同,可以得到相同压力条件下的三次样条函数系数向量分别为Di(1×n)、Ci(1×n)、Bi(1×n)、Ai(1×n),基于最小二乘法可以建立温度向量t(1×n)与三次样条函数系数向量之间的函数关系如下:
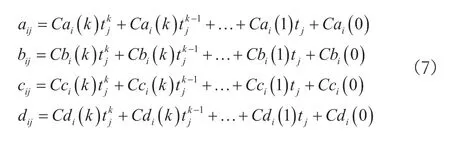
其中,区间[Fi,Fi+1]的三次样条插值函数系数为Cai(k)~Cdi(k),tj的最小二乘拟合多项式的系数即为aij~dij。
为明确非标定温度数值时输出压力F与输入压力p样条函数的差值节点Fi(i=1,2,3,…,m),选择利用牛顿插值法建立输出压力F与标定温度向量t之间的函数关系,可以得到下列函数,函数中的pi(输入压力)维持不变:
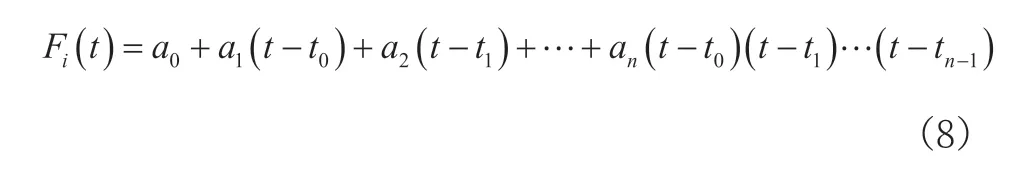
为明确[Fi,Fi+1]这一插值区间,选择将实测温度t输入上述函数之中,求得温度t条件下的三次样条函数插值节点Fi。
利用温度t对插值区间[Fi,Fi+1]的三次样条插值函数系数进行表达,如下:
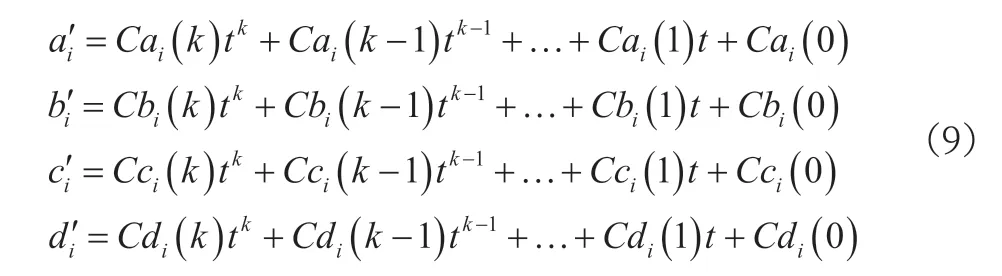
当环境温度数值为t时,需要先确认输出F所处的插值区间,确认之后将t代入其中,对子区间[Fi,Fi+1]的三次样条系数进行计算,求得由输出压力F构建的测量范围内任意压力数值的多项式,具体如下:
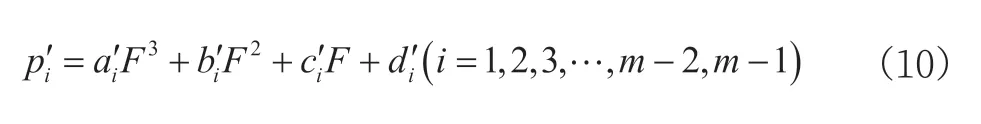
5 结果校验分析
基于JB/T 5537-2006 确定零点漂移与灵敏度漂移计算公式如下:

按照10℃的步长从-40℃~80℃温度区间范围内选择13个不同等级的温度进行测试,压力数值按照12 kPa 的步长从-40 kPa~40 kPa 范围内选取6 个不同等级的压力,共计78 组数据,模型的验证分析选择借助Matlab 软件来实现。由于本文所提出的数值分析模型应用的最小二乘法,为避免在多次拟合的情况下影响数值精度,设定拟合次数为2,对温度、三次样条函数进行曲线拟合。结果表明,室温20℃时误差为0.19%,次数的数值为最大值,此时的压力数值为-2.8 kPa。
选择利用下述公式对最大相对误差精度进行验证,如下:
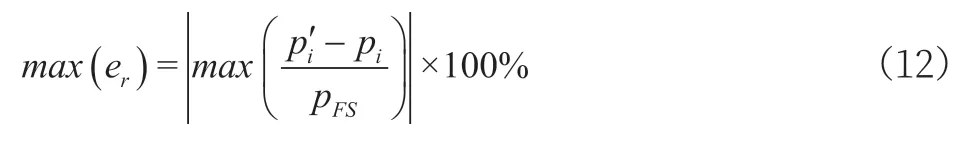
其中,pi为输出压力(补偿前),p’i为输出压力(补偿后),pFS即为最大测量压力。
为验证灵敏度误差与零点漂移在补偿模型处理后的效果,选择80℃、60℃、40℃、20℃、0℃、-20℃、-40℃几个不同的稳定对补偿前后的零点漂移与灵敏度误差进行计算,数据结果详情如表1、表2 所示。结果表明,零点漂移误差补偿前最高为-474.6 Pa,补偿后最高为5.597 Pa;灵敏度误差补偿前最高为15%,补偿后最高为0.2%;补偿效果良好。
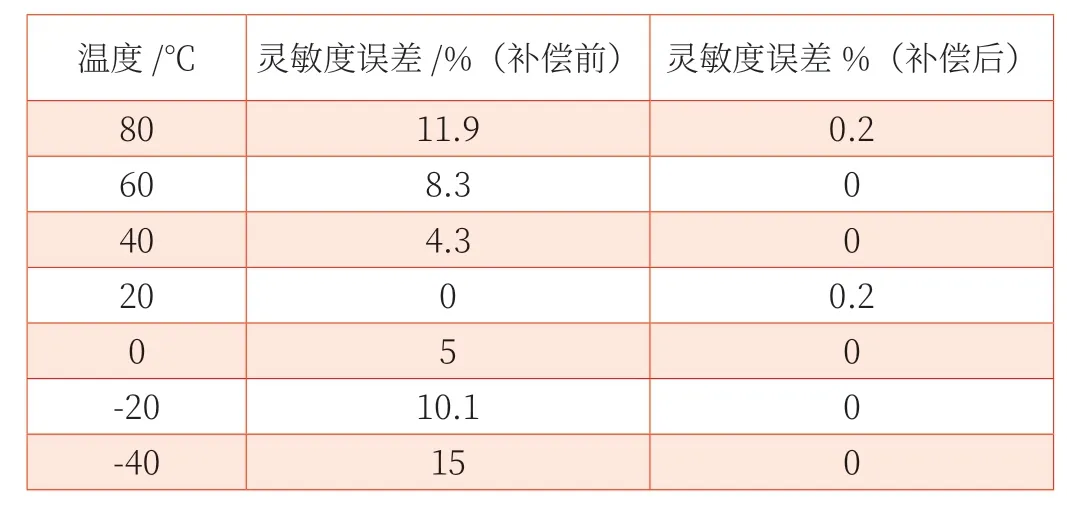
表1 补偿前后各温度下的灵敏度误差
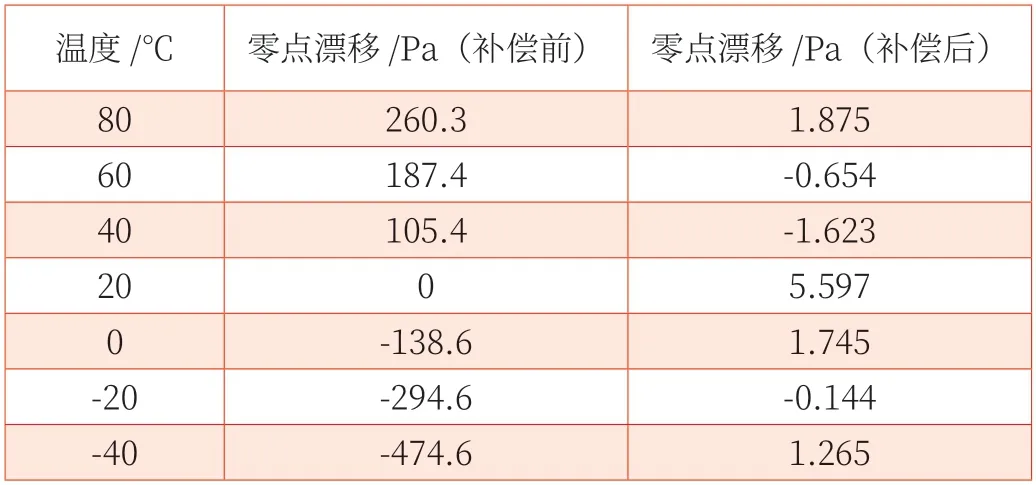
表2 补偿前后各温度下的零点漂移
6 结论
综上所述,本文基于最小二乘法、插值法提出了一种基于数值分析的新型压力传感器温度补偿方法。该算法模型在三次样条插值下实现了最小二乘法与牛顿插值法的融合应用,通过Matlab 仿真模拟的方式对算法模型的补偿效果进行了验证;结果表明,20℃、-2 800 Pa 时的相对补偿误差最大,数值为0.19%;通过补偿能够将零点漂移降低至5.597 Pa 以下,将灵敏度误差降低至0.2%以下,大幅度提升了压力传感器的测量精度,具有推广应用价值。

