带有随机系数的双线性INAR(1)模型的统计推断

范晓东，张 持，张庆春*，赵宸稷，曹晓涵

(1.吉林化工学院 理学院，吉林 吉林 132022；2.哈尔滨工程大学 计算机科学与技术学院，黑龙江 哈尔滨 150001；3.吉林化工学院 信息与控制工程学院，吉林 吉林 132022)

整数值时间序列在金融、交通、医疗、预防犯罪等很多领域都广泛存在.基于稀疏算子构建整数值模型是拟合整数值时间序列的主要方法.最早的稀疏算子模型是McKenzie(1985)[1]基于二项稀疏算子构建的整数值一阶自回归(INAR(1))模型.统计学者们针对INAR(1)模型进行了广泛研究[2-4].由于稀疏参数会受到外部环境的影响而随时间变化，Zheng等(2007)[5]提出了带有随机系数的一阶整数值自回归(RCINAR(1))模型，拓广了INAR(1)模型的应用范围，但该模型不适用于拟合非线性的整数值数据.在传统的时间序列分析中，为了拟合地震和疾病暴发等带有偶然爆发特征的时间序列，Mohler(1973)[6]提出了双线性模型(Bilinear model).Granger和Anderson(1978)[7]将双线性模型应用到时间序列建模中.双线性模型是类似线性ARMA模型的一种非线性模型，它保留了大部分ARMA模型结构的特性，它的另一种常见形式是仅具有AR结构的模型.它比线性模型能更好地拟合现实生活中的非线性时间序列数据，同时它也是时间序列非线性模型中形式最简单的一类模型.Tong (1989)[8]将双线性模型引入到整数值时间序列建模中.Doukhan等 (2006)[9]和 Drost等(2008)[10]先后对带有独立新息过程和生存过程的双线性整数值时间序列模型进行了研究.由于该模型的自回归系数是固定的，所以无法刻画受环境等因素影响随时间变化的动态整数值时间序列.因此，为刻画随时间变化的整数值时间序列，本文基于带有随机系数的二项稀疏算子建立一阶自回归双线性模型，称为带有随机系数的双线性非负整数值一阶自回归(RBLINAR(1))模型，并用修正的矩估计法估计模型参数，具有一定的创新性和实用价值.

1 模型及其性质

1.1 RBLINAR(1)模型

称满足迭代方程(1)的过程为基于带有随机系数的二项稀疏算子的双线性INAR(1)过程,记作RBLINAR(1)过程.

(1)

其中“°”表示随机系数的二项稀疏算子，其定义如下：

(2)

注意到，当{εt}已知， {Xt}未知时，RBLINAR(1)模型对于{Xt}而言是线性的，反之若已知{Xt}，{εt}未知时，RBLINAR(1)模型对于{εt}而言是线性的，因此该模型是双线性模型.

1.2 RBLINAR(1)模型性质

设{Xt}是由(1)式定义的一个RBLINAR(1)过程，其条件矩和矩分别为：

(3)

(4)

(5)

(6)

(7)

(8)

E(εt|Ft)=max{0,Xt-αpXt-1λ},

(9)

E(Xt+1|Ft)=αpXtmax{0,Xt-αpXt-1λ}+λ,

(10)

下面给出统计性质(4)和(6)的证明，其他性质推导过程类似.

证明(4)：

得证.

(6)：

由稀疏算子性质有：

E(α°X)2=α(1-α)E(X)+α2E(X2),

带入E(Xtεt)2中得到：

由{Xtεt}严平稳，E(Xtεt)2=E(Xt-1εt-1)2进而可以推出:

得证.

2 参数估计

(11)

(12)

(13)

3 数值模拟

针对模型(1)，对模型参数的修正矩估计量进行数值模拟，选取下面4组参数：

(A)p=0.2,α=0.5,λ=1,(B)p=0.2,α=0.5,λ=2,(C)p=0.2,α=0.5,λ=3,(D)p=0.3,α=0.4,λ=1, 分别在样本长度为100,500,1 000,5 000时借助R 软件重复模拟1 000次取估计的经验偏差(Bias)，均方误差(MSE)进行分析，结果见表1.例如表中(0.1136,13.762 9)，表示经验偏差(Bias)为0.113 6，均方误差(MSE)为13.762 9.

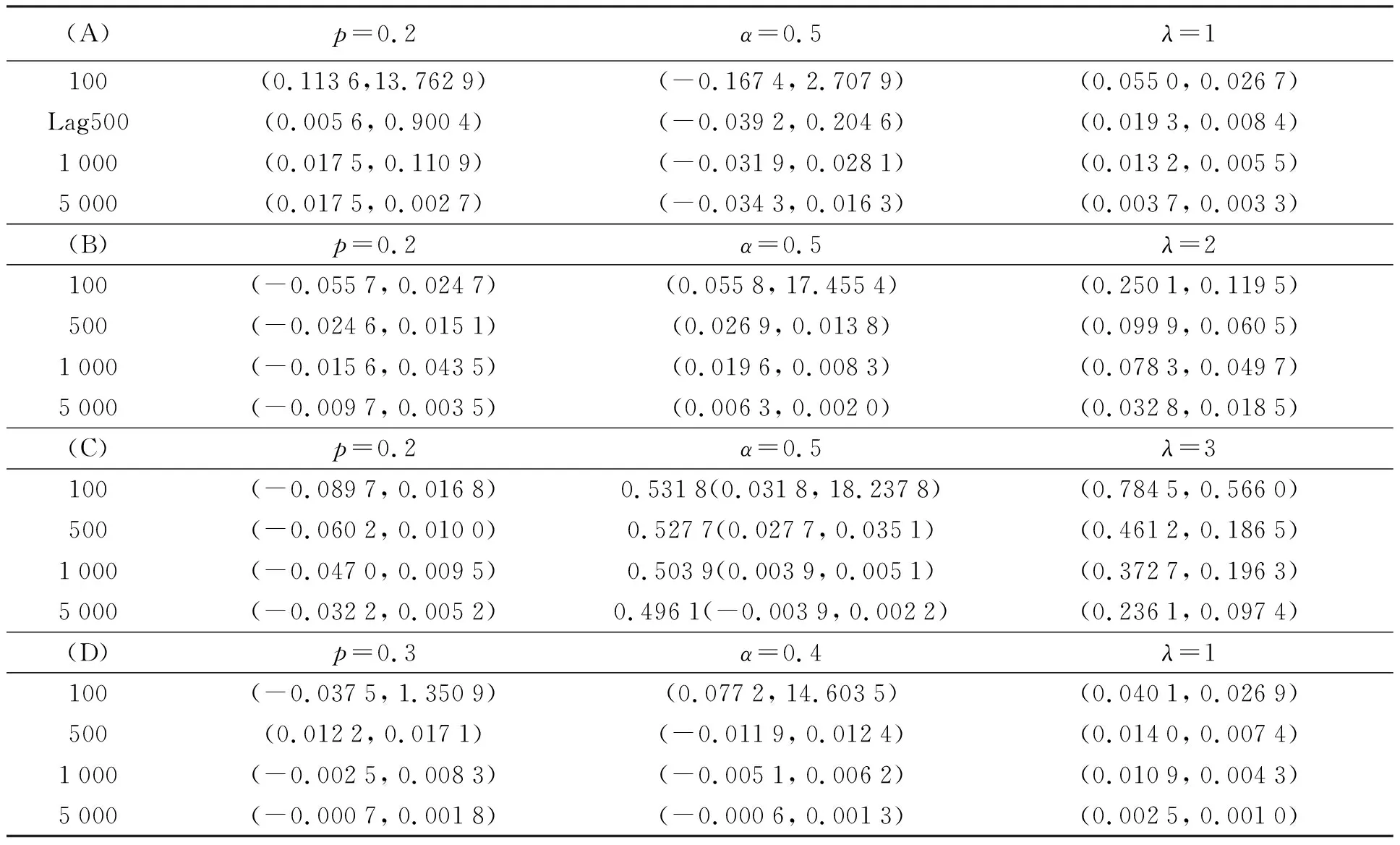
表1 RBLINAR(1)模型参数估计的经验偏差和均方误差

通过分析表1的模拟结果得到：模型参数的估计值随样本长度n的增加逐渐收敛到真实值，均方误差MSE和偏差Bias会逐渐减小.当α、P取值不变时参数样本长度为100时，参数λ取值越大，估计的偏差及均方误差越大.但当样本长度超过500时对任一组参数，估计效果良好.说明本文提出的修正的矩估计量具有渐近性，估计方法可行.

4 实例分析

为阐明模型的应用，选用曼哈顿地区2008年至2018年的月度偷窃记录数据，共132个观测值.图1～2分别给出了该序列的样本路径、ACF图和PACF图.从图1可以看出：序列没有明显的趋势，大致是平稳的.图2中，从自相关(ACF)图可以看出，自相关图是拖尾的，从偏自相关图中可以看出：序列存在很重要的一阶相关关系，所以可以建立INAR(1)模型来拟合该序列.

下面考虑本文提出的RBLINAR(1)模型和其他的3个模型： (1)基于二项稀疏算子的新息过程为泊松分布的INAR(1)模型；(2)基于负二项稀疏算子的边际分布为几何分布NGINAR(1)[8]；(3)带有随机系数的基于二项稀疏算子边际为泊松分布的RINAR(1)模型.

基于条件期望下向前一步预测的均方根误差，将4个模型比较，结果见表2，表中Na表示该参数在模型中不存在.

表2结果显示RBLINAR(1)模型的均方误差最小，所以RBLINAR(1)模型是更适合该数据集的模型.

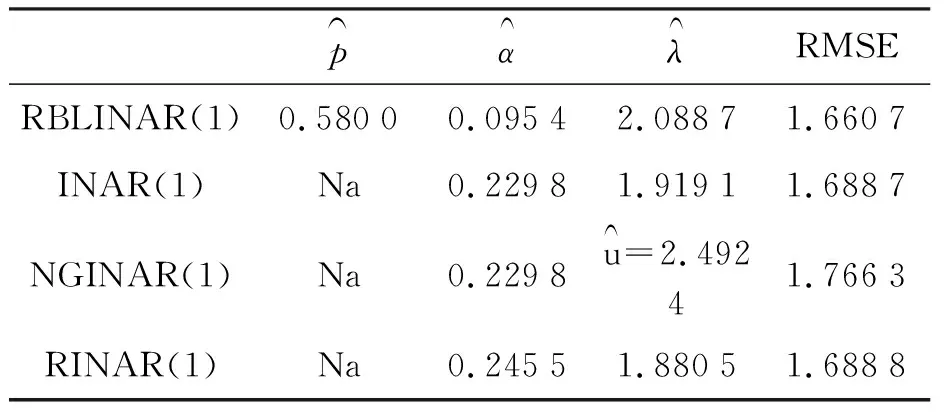
表2 月度偷窃数据的模型及估计结果

5 结 论

基于带有随机系数的二项稀疏算子构建了双线性非负整值一阶自回归(RBLINAR(1))模型，推导出了模型的统计性质并利用修正的矩估计法估计模型中的未知参数.通过数值模拟对模型的估计方法进行了评估，数值模拟结果显示，模型参数的估计值随样本长度增加逐渐收敛到真实值，均方误差和偏差会逐渐减小，说明修正的矩估计量具有渐近性，估计方法可行.通过给出实际数据说明了模型的应用，通过对比4个模型的均方误差，得出RBLINAR(1)是更适合数据的模型.