灰色时序模型在建筑物沉降观测中的应用
潘顺宇,付 饶
(1.山东正元数字城市建设有限公司,山东 烟台 264670)
灰色时序模型是一种应用广泛的预测模型,在植被生长、社会发展、货运储量、建筑沉降等方面都有比较成熟的改进模型[1-3]。灰色模型限制于自身的响应式组成,导致在长期预测中会出现比较明显的指数增长趋势,这种增长趋势在建筑沉降预测中与实际沉降情况会有所出入[4-7],相关学者对此方面的改进工作有较多研究[8-9]。本文在前人工作的基础上,首先验证了背景值优化中梯形公式的作用充当近似的数值积分公式,然后根据牛顿柯达斯系数表讨论各种情形下背景值优化的方法与积分区间,并结合傅里叶级数的残差修正方法对灰色模型进行进一步改进。
1 灰色时序模型

由以上变化,且X(0)和X(1)之间满足式(2)所示的关系:
对X(1)进行变换,生成紧邻均值序列z(1)(t),如式(3)所示:式中,t=2,3,…,n,至此可得灰色模型的基本形式如式(4)所示:
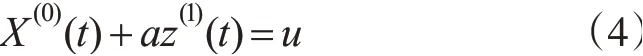

根据最小二乘准则求式(4)的最小二乘解,其参数a、u计算如式(5)所示:
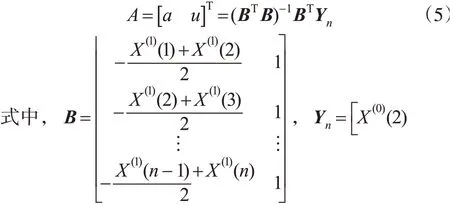
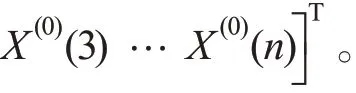
则灰微分方程为:

令X(1)(1)=X(0)(1),可得X(1)(t)。

对累加公式(1)进行改写,将最后一项从累加符号中单独列出。

将式(8)进行移项,得到一次累减还原后的原始序列。

以上过程即为传统灰色时序模型的预测过程,在此基础上,对灰微分方程式(6)在[t-1,t]上积分。
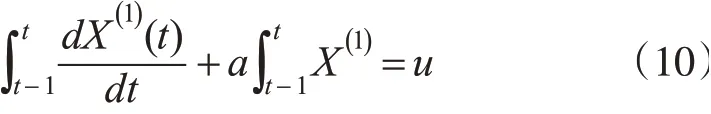
根据积分理论展开等式左侧第一项。
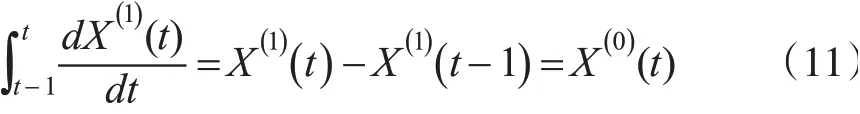
使用梯形公式代替式(10)左侧第二项。
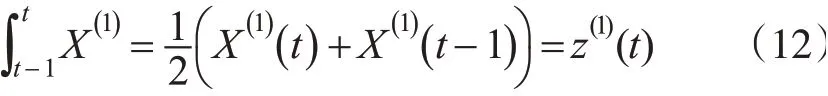
综合以上各式可得与式(4)完全一致的灰色模型,以上推导说明灰微分方程中的第二项积分使用梯形公式代替时,该式与灰色模型的白化方程是形式一致的。考虑到数值积分中存在辛普森公式、柯达斯公式等其他积分替代公式,下面介绍使用其他形式的数值积分代替梯形公式的情形。
2 数值积分改进的灰色时序模型
数值积分公式来源于牛顿柯达斯公式,根据柯达斯系数表,可以得到不同阶次的数值积分公式,柯达斯系数关系如表1所示。

表1 部分Cotes系数
由表1可知,根据数值积分可得n=1,2,3,4时的数值积分公式,分别对应T(梯形公式),S(辛普森公式),Q(n=3),C(柯达斯公式),如式(13)~(16)所示。
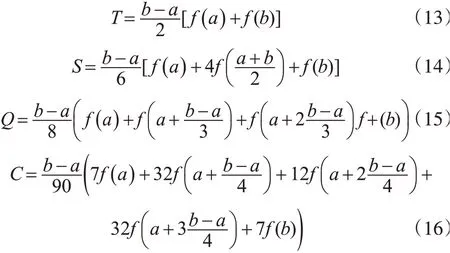
对式(16)进行积分,由于式(13)~(16)中,步长函数是根据积分区间确定的,因此对不同阶次的数值积分公式,应选择其n取值长度的积分区间,以确保步长公式能取到函数的整值,这一点是确保使用数值积分改进后计算公式依然能使用离散点的前提,常规灰色时序模型已经使用式(13)的公式,下面列出其他三式改进的灰色模型。
n=2时,积分形式如式(17)所示:
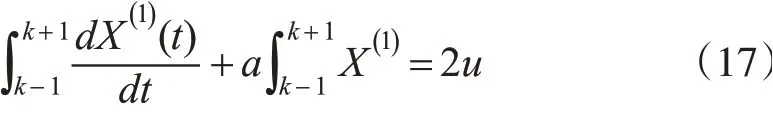
将式(17)左侧第一项展开,如式(18)所示:
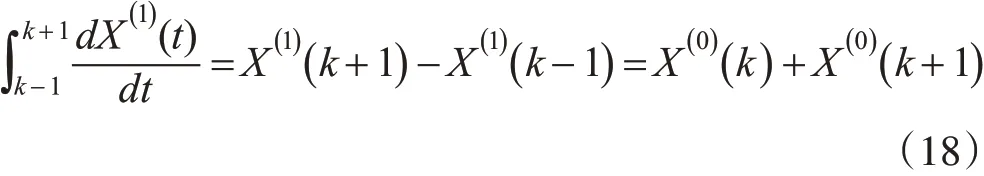
使用n=2的数值积分公式代替式(17)左侧第二项,如式(19)所示:

式(17)可为式(20)所示的形式:
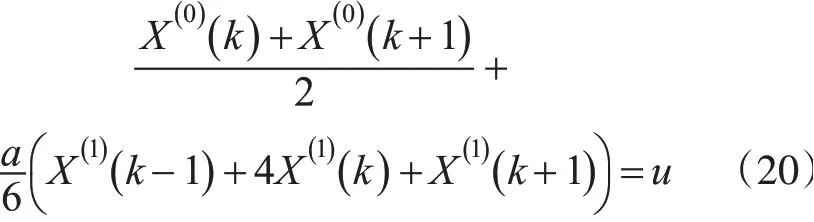
改写为矩阵形式,如式(21)所示:

求式(21)的最小二乘解,解算式同式(5),参数变化如下:
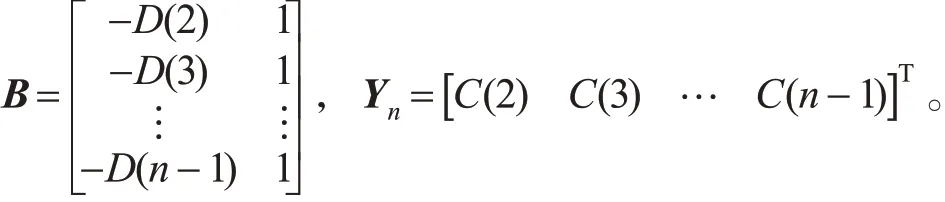
n=3时,积分形式如式(22)所示:
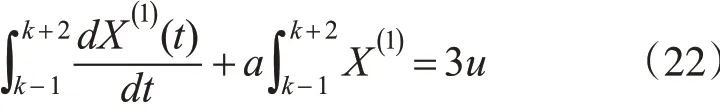

将式(22)左侧第一项展开,如式(23)所示:使用n=3的数值积分公式代替式(23)左侧第二项,如式(24)所示:
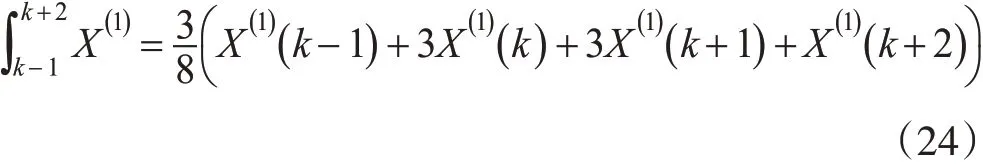
式(22)可为式(25)所示的形式:
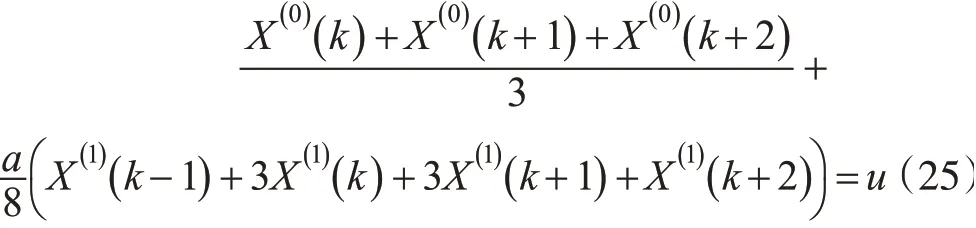
n=4时,积分形式如式(26)所示:

将式(26)左侧第一项展开,如式(27)所示:

使用n=4的数值积分公式代替式(26)左侧第二项,如式(28)所示:
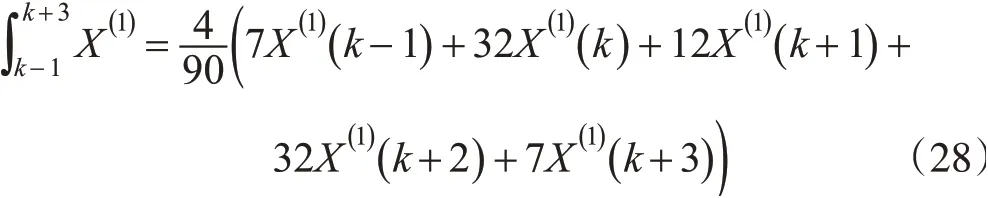
式(26)可为式(29)所示的形式:
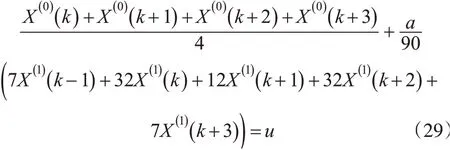
3 基于傅里叶级数的残差修正
为方便与上述推导区分,残差修正部分对灰色模型所用的符号标记进行了更改,原始序列和预测序列的残差序列如式(30)所示:
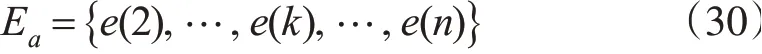
式中,e(k)=X(0)(k)-X^(0)(k),2≤k≤n。
将上式中残差序列用傅里叶级数表示如式(31)所示:
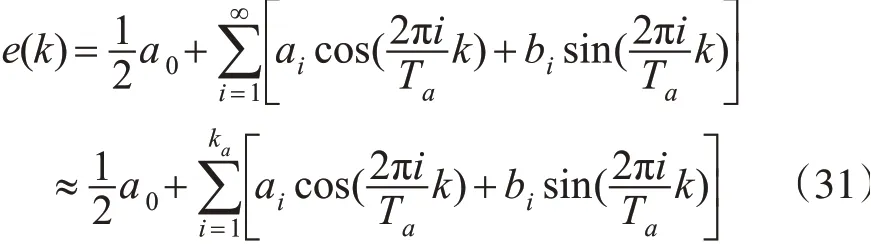

式(31)整理成矩阵形式如式(32)所示:

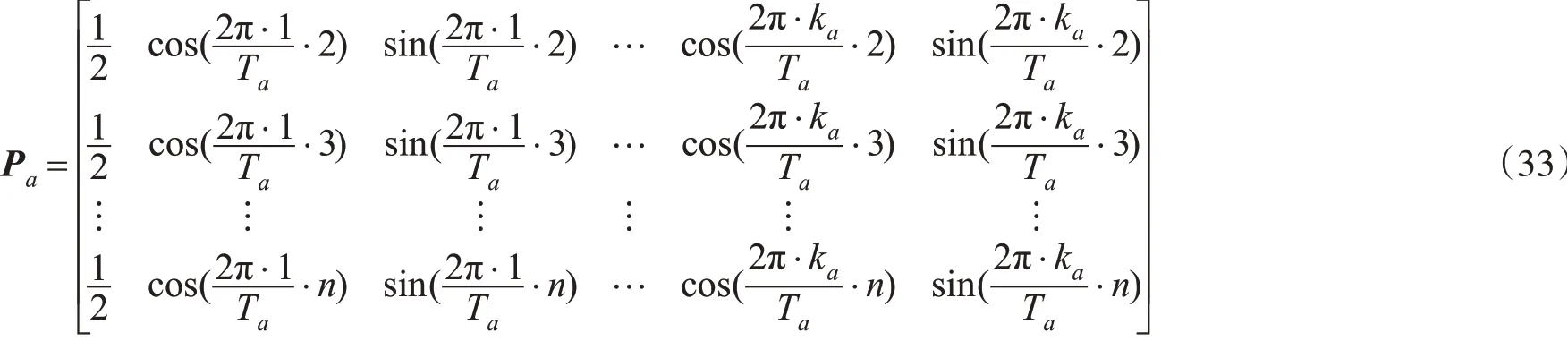
系数解算如式(34)所示:
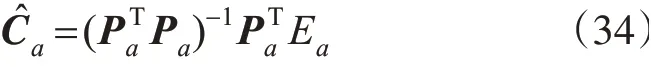
将系数值代入到式(31),求得残差序列E^a(k)如式(35)所示:

4 实例验证
本文所用验证数据,为某建筑沉降监测的15期成果,监测时间为2014-05~2016-01,测量中误差为0.72 mm,其中前九期用于计算模型参数,后六期用于验证模型精度,为说明本文所提及的数值积分改进的灰色模型的计算方法,以下将基于柯达斯公式改进的系数计算过程列出。
柯达斯公式计算过程如下:
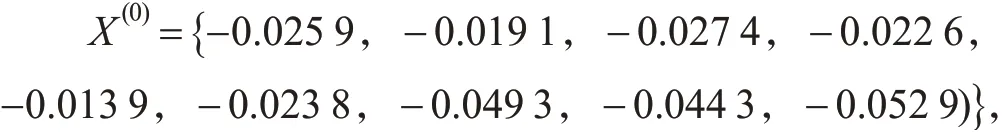
将按X(0)式(1)累加形成X(1)(t):

按式(3)生成紧邻均值序列z(1)(t):

此时式(21)中,B=[-0.067 0,-0.091 0,

按照式(5)解算系数结果为:[au]T=[-0.198 6-0.149 6]T。
分别使用T(梯形公式),S(辛普森公式),Q(n=3),C(柯达斯公式)结合灰色模型进行沉降参数计算,前九期拟合成果与真值的差值如表2所示。
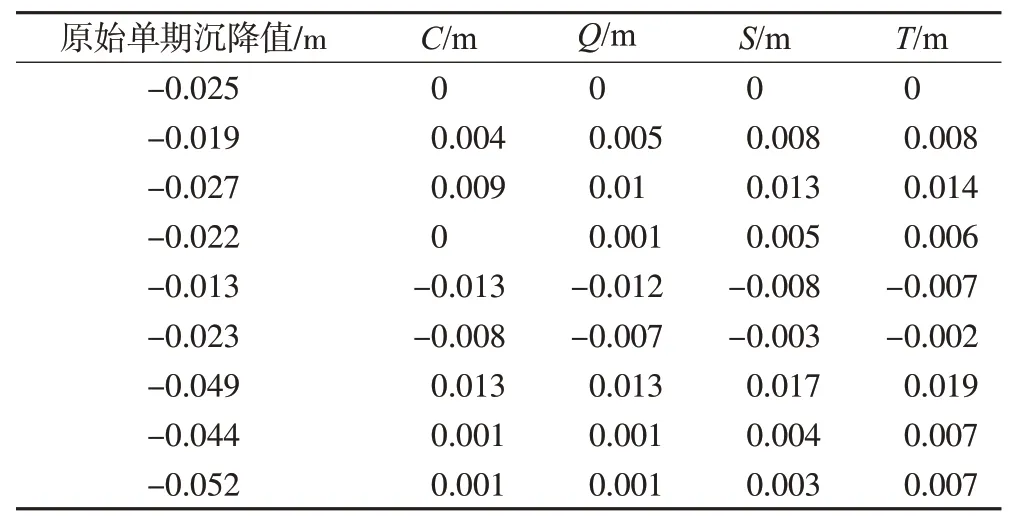
表2 拟合成果与真值的差值对比
表2的拟合成果中,4种模型未有明显的精度区别,从数值上看,内符合精度相当,但其差值分布情况不同,差值增大或减小与n的次数未有明显的线性规律,有关本部分成果的使用将在后续的残差修正中提及。后6期的预测成果如表3所示,在预测精度评定中使用真误差和绝对值的平均值作为衡量标准,图1为小数制的曲线。

表3 预测成果误差对比
由表3及图1,可以看到C和Q公式下的灰色模型预测精度已经非常接近,各期预测精度较高,且随期数推移的误差增长比较平缓;S和T公式的预测精度不仅偏低,且其误差不稳定。随着预测时间的推移,误差的绝对值会接近或突破10 mm;本组验证说明数值积分的改进对灰色模型背景值平滑起到了比较明显的作用,但在n=2时其改进效果并不明显;在n=3时即可达到较高的预测精度,随着n的增大,最小二乘解算式中的系数矩阵会减小行维度,考虑到灰色模型经常应用在少数据的情形中,因此在原始序列较短的情况下可以选择使用n=3的改进公式,其精度相较n=4时损失较少。
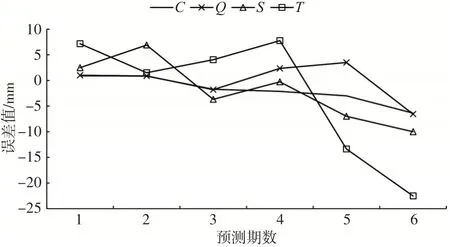
图1 预测曲线
下面结合傅里叶级数的残差修正方法验证本文使用的几种灰色时序模型与该修正方法的适用性,由于傅里叶级数系数解算过程矩阵较大,因此没有列出代入数据的矩阵计算过程,残差修正的大致思路如下:
1)计算表2的差值成果,以此作为式(30)的差值成果。
2)根据傅里叶级数的残差修正方法进行参数计算,得到式(35)所示的残差修正计算式。计算表3的预测成果。
3)根据式(35)计算表3中各期预测成果的残差修正值。将修正值改进到表3的预测成果中,完成基于傅里叶级数的残差修正。
根据以上过程,计算表3预测数据的傅里叶级数残差修正成果,如表4所示,图2为小数制的表4曲线。
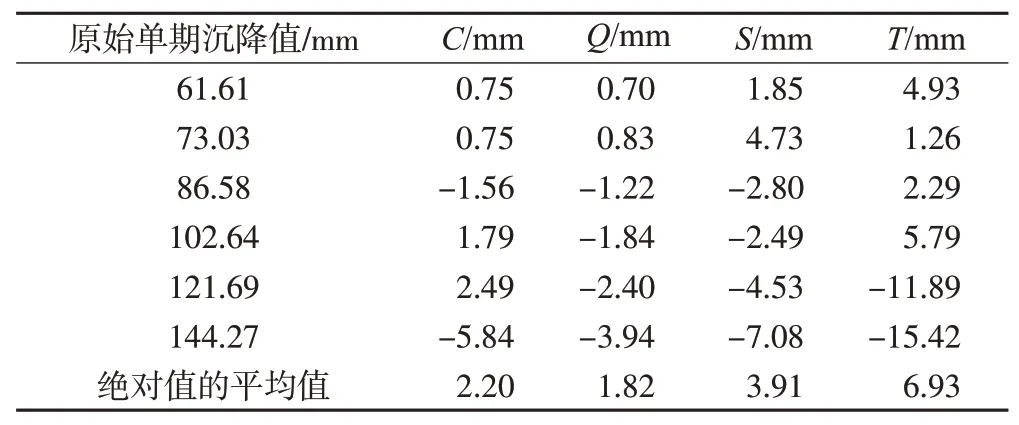
表4 残差修正的预测成果误差对比
由表4和图2可知,傅里叶级数改进后4种模型的平均误差都有所下降,不同的模型下降0.5~3 mm不等,但傅里叶级数的残差修正并不能非常明显地提升精度,例如T的平均修正误差为6.93 mm,依然低于S未修正的5.06 mm,说明这种残差修正方法可以在原模型的范围内提高精度,但不能克服模型自身精度偏低的缺陷。其中Q的平均误差经过改正已经低于C,这与Q和C未改正的平均误差本来就接近有关系,因此不能说明Q的残差修正成果精度一定高于C,但是此处的成果验证了前文的结论,在原始序列较短的情况下可以选择使用n=3的改进公式。
5 结论
本文讨论了数值积分在灰色时序模型中的背景值优化方法,通过实例验证了其优化效果,当n取3、4时,背景值优化能够比较明显地提升沉降预测精度,本文实例中的平均误差分别为2.50 mm和2.68 mm。基于傅里叶级数的残差修正方法在各种背景值优化方案中均能提高预测精度,但未能起到越级精度提高的效果,当n取3时其预测精度高于n取4的方案,平均误差为1.82 mm。在实际预测中,基于傅里叶级数残差修正的n取3与n取4的2种数值积分改进方案均能获得较高的沉降预测成果,可以根据原始序列的长度灵活选择使用。

