基于两杆三索张拉整体结构的可变径柔性步行轮设计

孙建伟 栾亦鹏

长春工业大学机电工程学院，长春，130012

0 引言

随着机器人技术的发展，移动机器人的应用范围逐步从室内扩展到野外和灾区，使得移动机器人在非结构化环境中的移动性能显得非常重要。传统的轮式机器人车轮结构简单，自由度少，易于控制，运动稳定，可以在低耗能的情况下实现高速运动，广泛应用于多个领域[1]，但它无法攀爬或者翻越与其尺寸相同或者更大的障碍物，其移动性能在崎岖的地形上受到了严重的限制。与轮式机器人相比，腿式机器人[2-5]的主要特点是应用广泛，它们可以很好地适应结构化或者非结构化地形[6]，但缺点是移动速度相对缓慢，控制系统相对复杂，需要配备大量的制动器来为其提供所需要的能量。

近年来，国内外学者对机器人的研发工作已取得了显著成绩。例如:天津大学提出一种利用躯干运动来实现四足机器人倾翻后自我恢复的变胞四足机器人[7],它可通过轮履结构的转换在灾难现场等复杂环境中高效地解救和运送伤员；天津理工大学研究了一种新型轮履复合式救援机器人[8]；韩国首尔国立大学设计了一种基于折纸机构的变径折纸车轮机器(Origami Wheel Transformer)[9]；在此基础上，又提出了一款高负载容量折纸可变换车轮，该车轮使用复合膜折纸技术，大大提高了车轮的负载能力[10]；美国凯斯西储大学提出了基于一种独特齿轮机构的轮腿切换型机器人WheeLeR[11];都灵理工大学提出一种操作模式会根据地面条件进行调整的多地形移动轮式机器人[12]；密歇根大学提出一种动力自主、不受束缚、具有柔顺腿的六足机器人RHex[13-14]，RHex机器人可通过对机器人动态性能的控制,依靠动态反馈来实现自我恢复。

轮式机器人在结构化地形上具备快速移动能力，但在非结构化地形上机动性较差。与之相反，腿式机器人在非结构化地形上拥有良好的机动性能，但在结构化地形上移动速度不足。因此研究一种同时具备轮式机器人快速移动能力和腿式机器人良好越障能力的轮腿复合型机器人具有重要的意义[15-16]。

1 张拉单元结构设计与稳定性分析

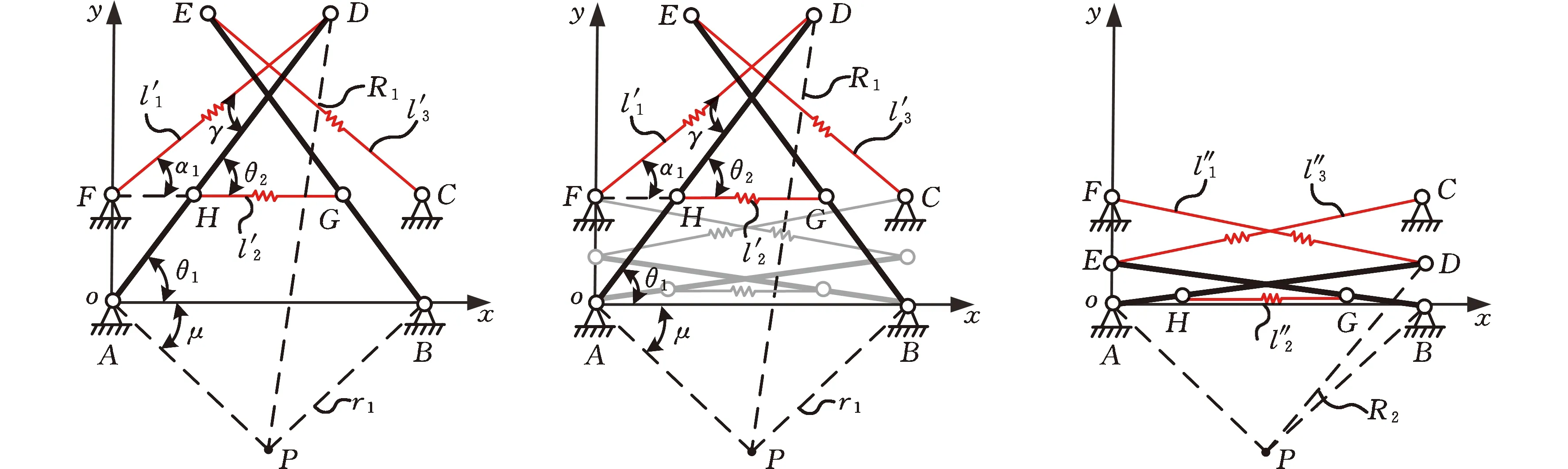
图1a所示为两杆三索平面张拉整体结构，它是通过改变两杆三索张拉整体结构中受拉构件(拉伸弹簧，以下简称弹簧)与受压构件(以下简称杆)的相对位置关系而提出的一种新型张拉变径步行单元结构。在坐标系oxy中，点A、B分别位于x轴上，且点A与坐标系原点o重合。在图1a的基础上，将点A拆分成固定点A和弹簧，将弹簧连接于点E、F上，将点B拆分成固定点B和弹簧，将弹簧连接于点D、C上，如图1b所示。在图1b的基础上，将两侧弹簧EF、DC取下，将弹簧分别连接于点D、F和点E、C上。将点F移动到y轴上，点C移动到与点F同一水平线上，且点C、F的连线平行于x轴。将弹簧ED向下垂直方向移动，使得弹簧ED连接在受压杆AD与BE上，并且将其固定在铰点H、G上，点H、G与点F、C位于同一水平线上。保证弹簧HG与x轴平行，如图1c所示。此时，杆AD与杆BE作为受压杆的同时也起到支撑作用。图1d为点E、D同时受到向下的力时，张拉单元形变过程图。

(a)基本张拉单元 (b)张拉单元变化过程 (c)新型张拉单元

完全展开状态Ⅰ Ⅰ→Ⅱ 完全收拢状态Ⅱ(d)张拉单元受力形变过程图1 基本张拉单元的变化过程图Fig.1 Change process of basic tensegrity unit

图2为张拉变径步行轮单元结构简图，图中给出了张拉变径步行单元完全展开和完全收拢状态。如图2所示，在坐标系oxy中，点A与坐标原点o重合，点F坐落于y轴上，点C、H和点G与点F位于同一水平线上且与x轴平行，点B位于x轴上。步行轮中心点P距离点B的距离为r1，与点A的连线和x轴所成的夹角为μ。

定义杆AD和杆BE的长度为LAD和LBE，且LAD=LBE，点A到点H的距离长度为LAH。杆AD的长度为杆AH长度的n倍。定义每根弹簧的刚度系数同为K，弹簧FD的原始长度为l1，弹簧HG的原始长度为l2，弹簧CE的原始长度为l3，且l1=l2=l3。定义弹簧FD的稳定长度为l′1，弹簧HG的稳定长度为l′2，弹簧CE的稳定长度为l′3，且l′1=l′3。杆AD与x轴夹角为θ1，杆AD与弹簧FD在点D的夹角为γ，与拉伸弹簧HG在H点的夹角为θ2，因为拉伸弹簧HG平行于x轴，因此θ1=θ2。当θ1角度最大时，张拉变径步行单元处于完全展开状态，此状态下，张拉变径步行单元的最大半径为R1，此时拉伸弹簧FD与x轴所成夹角为α1。如图2所示，当张拉变径步行单元处于完全收拢状态时，杆AD与x轴夹角为θ′1，张拉变径步行单元的最小半径为R2。

完全展开状态Ⅰ Ⅰ→Ⅱ：θ1→θ′1，θ2→θ′2 完全收拢状态Ⅱ图2 张拉变径步行单元结构简图Fig.2 Schematic diagram of the structure of tensegrity variable-diameter walking unit

由于张拉变径步行单元是完全对称结构，所以l′1=l′3，当步行单元处于稳定状态时，得到三角函数关系如下：

(1)

(2)

l′2=2r1cosμ-2LAHcosθ1

(3)

α1+γ=θ1

(4)

α1≤θ10≤θ1≤60°

(5)

在计算张拉变径步行单元的总势能U时，需要知道弹簧的刚度系数K,因此我们需要对弹簧进行刚度匹配。当负载为F时，每对弹簧受到的拉力为Fi(i=1,2,3)，弹簧受到杆AD的压力为FAD，每根弹簧变化量为Δli，即

Δli=l′i-lii=1,2,3

由胡克定律可知：

Fi=KΔli

(6)

由水平方向受力平衡得

FADcosθ1=F2+F1cosα1

(7)

由垂直方向受力平衡得

F1sinα1=6F+FADsinθ1

(8)

(9)

张拉变径步行单元的总势能U表达式为

(10)

将式(1)～式(4)、式(9)代入式(10)得

(11)

M2=2r1cosμ-l2

将式(11)中U分别对θ1、α1求导:

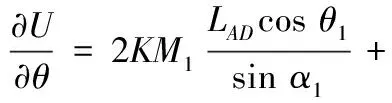
(12)

(13)

由式(12)和式(13)得

tanα1+tanθ1=0

(14)

由式(12)～式(14)可知，当式(14)成立时，张拉变径步行单元处于平衡状态，此时张拉变径步行单元存在自稳定状态。

张拉变径步行轮为多个相同的张拉变径步行单元所组成的封闭模型，工作原理为：基于单个张拉变径单元的顶点与地面接触，在车辆整体压力的作用下，张拉结构单元由极限展开状态向闭合状态运动，最后达到极限闭合状态。随着车轮的转动，当单个张拉结构单元离开地面时，张拉结构顶点受力逐渐减小，张拉结构单元由极限闭合状态向展开状态运动，最后回到极限展开状态。

在收缩、展开过程中，各个张拉变径步行单元具有相同的运动性能，因此选取张拉变径步行轮中两个相邻且相同的张拉变径步行单元进行组合，如图3所示。

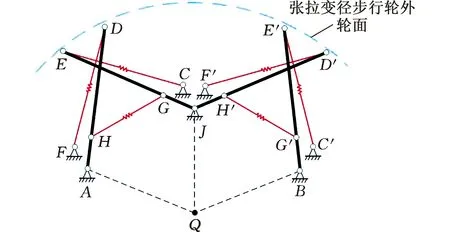
图3 张拉变径步行单元连接组合方式Fig.3 Connections and combinations of the tensegrityvariable-diameter walking unit

点Q为张拉变径步行轮的中心点，杆AD、JE、JD′、BE′为张拉变径步行轮内部支撑杆，点F、C、F′、C′为张拉变径步行单元中弹簧的固定点。点A、B、J是张拉变径步行单元在张拉变径步行轮中的固定点，且点J为两个张拉变径步行单元的连接点。点E、D、E′、D′所组成的外弧面为张拉变径步行轮的外轮面的一部分。

2 张拉变径步行轮轮毂的选择

根据张拉变径步行轮展收比最优原则对轮毂结构进行选择。图4所示分别是“正四边”、“正五边”和“正六边”轮毂结构，对应的角度μ依次为45°、54°和60°。

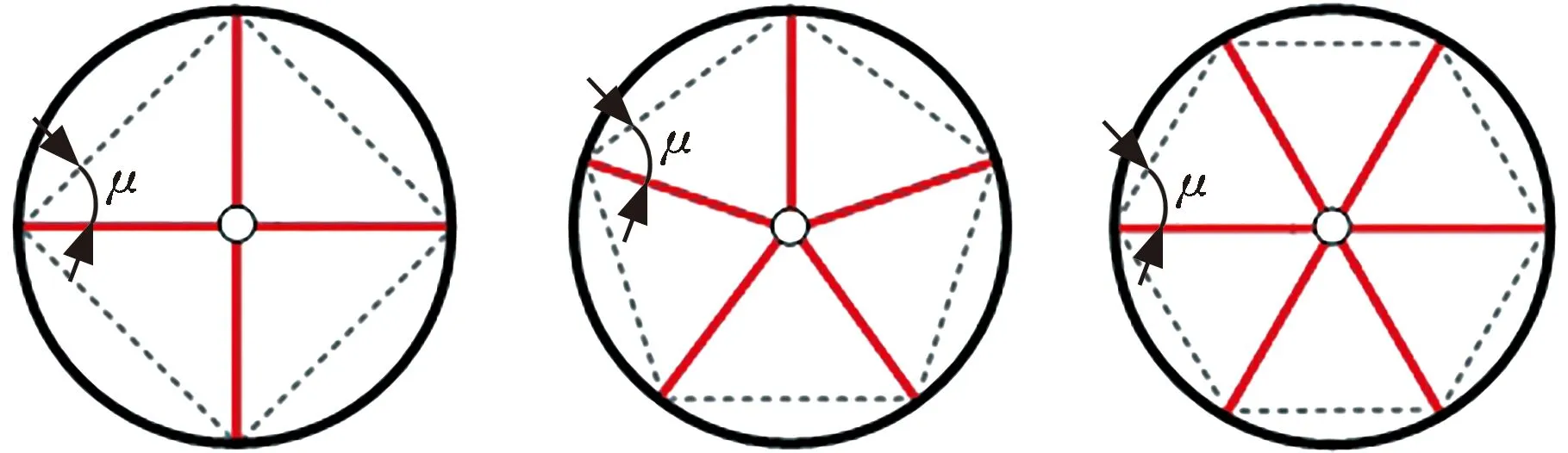
图4 不同轮毂的比较图Fig.4 Comparison diagram of different wheel hubs

张拉变径步行轮展收比η为步行轮完全展开姿态的最大半径R1与步行轮完全收拢姿态的最小半径R2之比：

(15)

(16)

(17)

根据张拉变径步行单元自稳定平衡状态下的单元边界约束条件(0≤θ1≤60°)，选取不同的轮毂结构和不同的角度θ1，依次计算张拉变径步行轮的展收比，计算结果列于表1。由表可知，当μ=60°，θ1=60°时，张拉变径步行轮的展收比可以达到最大，因此确定选择“正六边”轮毂结构。将n、θ1、r1、r2、li(i=1,2,3)、F代入式(1)～式(17)并利用MATLAB计算得出张拉变径步行轮结构的具体参数，见表2。

3 张拉变径步行轮模型建立与自由度约束

张拉变径步行轮整体是由多个组合结构组成的阵列结构，这些组合结构是由基本张拉单元和传动限位装置组成的。每个张拉变径步行轮包括6组张拉单元、传动限位结构和弧形胎面。传动限位结构包括导轨、滑块、钢丝绳等。

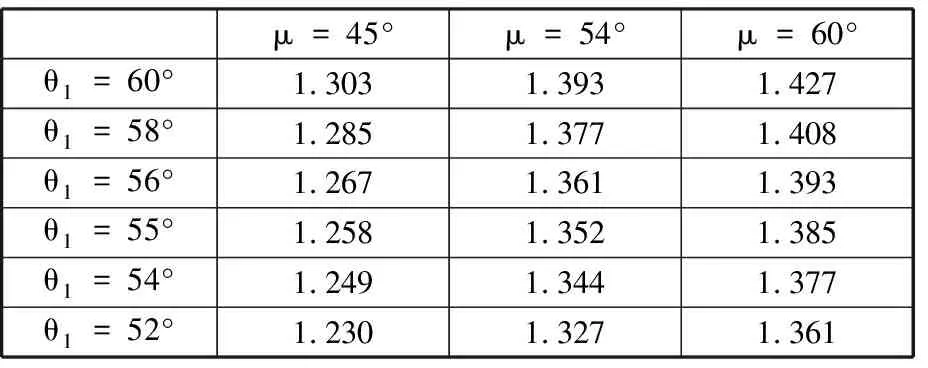
表1 不同轮毂结构下展收比η的计算结果

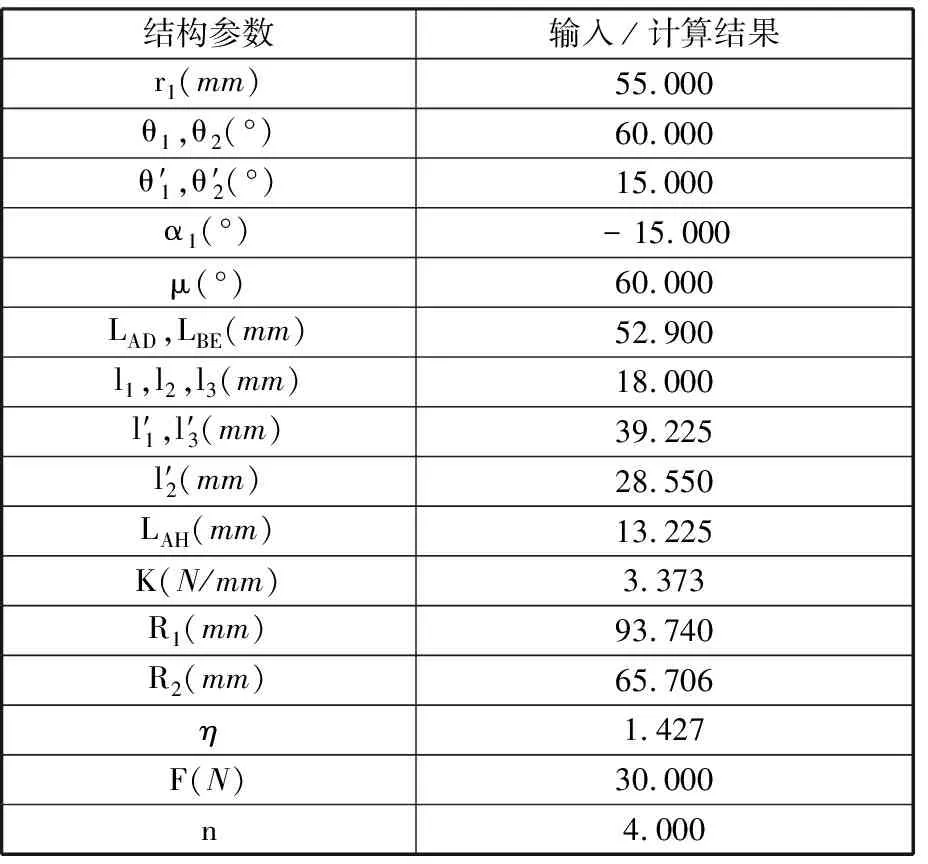
表2 张拉变径步行轮结构参数表

在结构方面，对原有的张拉变径步行单元进行了改变。为了保证张拉变径步行单元在变形过程中的径向分量不变，将3组弹簧通过钢丝绳、定滑轮等原件进行组合。首先，将弹簧FD、CE、HG取下，使用钢丝绳代替弹簧FD和弹簧CE。然后，将两个定滑轮分别固定于A点和B点。将一根钢丝绳的一端固定于E点，另一端向下延伸从固定于A点的定滑轮左侧绕过连接在弹簧HG左侧。同样地，另一根钢丝绳的一端固定于D点，另一端向下延伸从固定于B点的定滑轮右侧绕过连接在弹簧HG的右侧。此时，弹簧FD与杆AD重合，弹簧CE与杆BE重合，弹簧HG与AB点的连接线重合。两根连接于弹簧HF的钢丝绳代替了弹簧FD和弹簧CE，此时张拉变径步行轮单元结构依旧成完全对称结构。改变后的张拉变径步行单元虽然减少了弹簧的数量，但它与原始的两杆三索张拉单元结构等效，此结构下的张拉变径步行轮同样为自稳定平衡结构。

通过张拉结构的应用，基于张拉结构建立了轮式机构的框架，实现了轮式机构的柔性和强适应性。但是，当轮式机构达到运动极限位置时，由于张拉结构的柔性仍然存在，并且具备多个方向的自由度，如果不对其非径向的自由度进行约束，将会导致机构无法实现稳定，因此，为了提高机构的稳定性并保持轮式机构的自适应性，结合上文对轮式结构和运动方式的分析，设计了一种应用于张拉结构的轮式结构锁紧机构来约束其非径向自由度。

为限制张拉结构的自由度，在基本张拉单元中添加滑轨滑块(图5a)作为传动限位装置。在点E、D分别增加刚性杆，使其刚性杆一端节点分别固定于点E、D，另一端节点向上延伸固定于刚性节点G。如图5b所示，令点G与滑轨滑块相连。此时张拉变径单元其运动方向与滑轨滑块一致，由于滑轨滑块的作用，此时的张拉变径单元仅有径向自由度，且仅有一个受力点G，保证了结构的稳定性。张拉变径单元与滑轨滑块组合后的单元如图5c所示。通过图5c中的张拉变径步行单元，我们得到张拉变径步行轮整体模型如图5d所示。

(a)传动限位机构 (b)基本张拉单元

(c)限位后张拉单元(d)张拉变径步行轮模型图5 张拉变径步行轮建模Fig.5 The modeling of tensegrity variable-diameterwalking wheel

4 实验与分析

为验证张拉变径步行轮的越障性能以及减振能力，设计了一种由4个相同的张拉变径步行轮组装在一起的四轮车辆。该四轮车辆采用轮腿两种结构，当四个张拉变径步行轮为全闭合状态时，此时车辆为轮式结构，适用于车辆在平缓路面行驶，减小路面冲击，从而可实现高速运动状态；当车辆遇到不规则路面时，张拉变径步行轮由轮式结构转换成腿式结构，此时张拉变径步行轮为展开状态，以实现越障能力，提高车辆的通过性。

4.1 张拉变径步行轮爬坡实验

实验旨在验证张拉变径步行轮在攀爬起伏地面的自适应性和稳定性。

车辆前轮与后轮轴心之间距离为400 mm，张拉变径步行轮理论展开最大直径为189 mm,理论收缩最小直径为132 mm。当车辆在攀爬起伏地面过程中，车辆前轮与后轮轴心在同一水平线，此时车辆前轮直径为理论收缩最小值，后轮直径为理论展开最大值，此时车辆可爬理论角度β约为4°的斜坡。

在本实验中，张拉变径步行轮所组成的车辆前轮处于极限收缩状态、后轮处于极限展开状态时，采用坡度约为4°的坡体来测试车辆攀爬起伏地面的性能，如图6所示。本实验证明了张拉变径步行轮所组成的车辆具有良好的爬坡能力，并且在爬坡过程中可保持车辆整体水平，如图7所示。同时该车辆可根据所需要爬坡的角度来调整整体尺寸以及张拉变径步行轮大小的尺寸以适应不同角度的斜坡，该实验验证了张拉变径步行轮具有良好的自适应性以及爬坡能力。

图6 车辆爬坡实验Fig.6 Climbing experiment of vehicle

图7 车辆在攀爬起伏地面时保持水平状态(mm)Fig.7 The vehicle keeps a horizontal state when climbingthe undulating ground(mm)

4.2 张拉变径步行轮转弯实验

普通轮式机器人在实现转弯过程中通常需要配备完整的控制系统来帮助其完成该操作，由于控制系统的复杂性以及机器人整体质量增大，使得机器人实现转弯过程的局限性更大。

张拉变径步行轮所组成的车辆转弯的实验原理为：通过张拉变径步行轮的轮径调整，使得车体两侧车轮的轮径尺寸存在差值，以此来实现车辆左右转弯操作。

当车辆需要左转时，车辆左侧车轮变为收缩状态，右侧车轮为展开状态，驱动电机转动，车辆在向前行驶过程中，由于车辆右侧车轮半径大于左侧车轮半径，车辆会向左进行转弯。右转同理。图8显示了张拉变径步行轮所组成的车辆通过其车轮尺寸的差异性来实现转弯的实验过程。图9所示为张拉变径步行轮所组成的车辆在转弯过程中转弯角度φ的变化。

图8 转弯实验Fig.8 Steering experiment

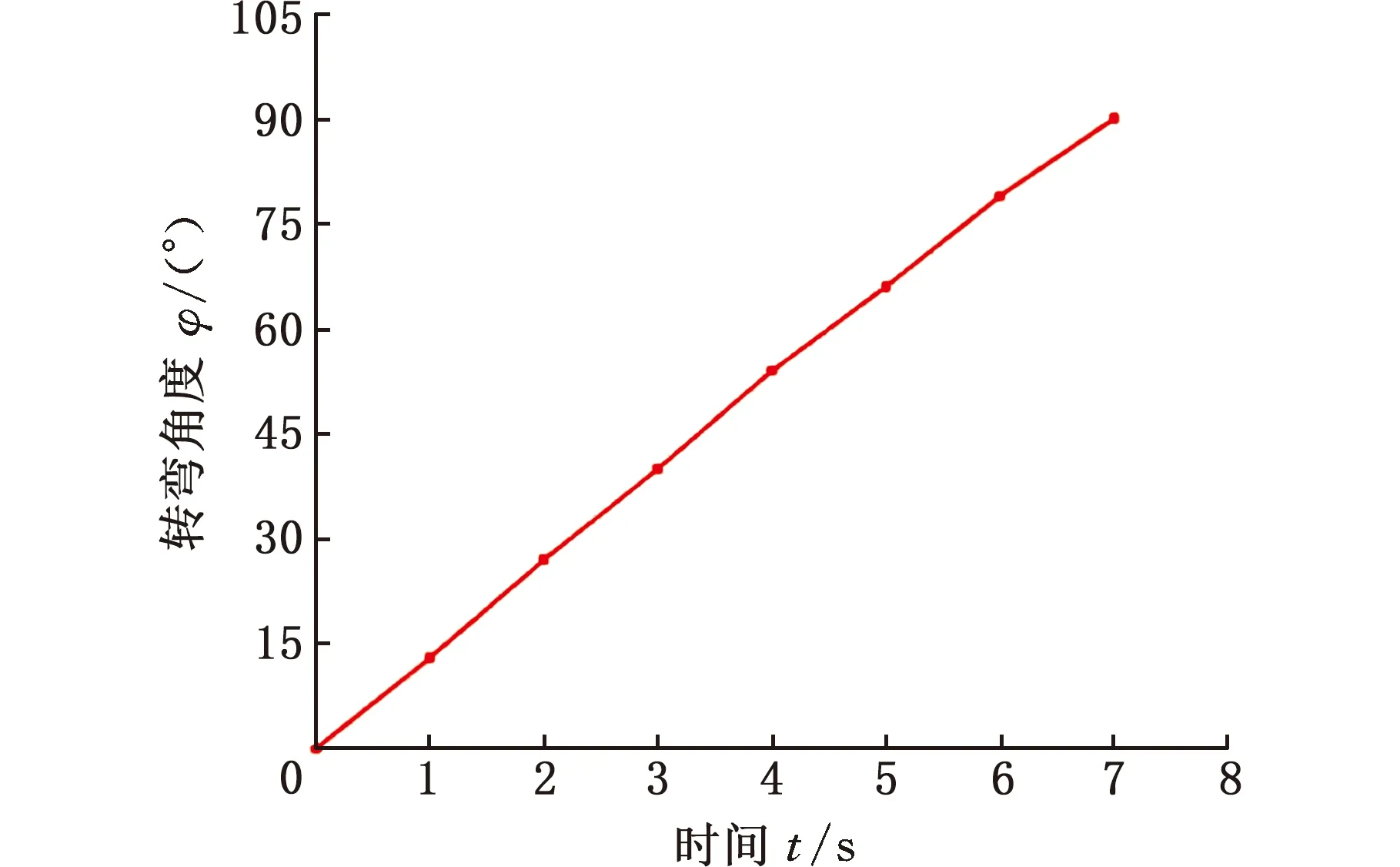
图9 车辆的角度变化图Fig.9 Angle change diagram of vehicle

4.3 张拉变径步行轮弹性测试实验

张拉变径步行轮由6个张拉单元构成。张拉结构使得张拉变径步行轮具备一定柔性，拥有良好的弹性及缓冲能力，为张拉变径步行轮提供了良好的自适应能力以及减振性能。

为了验证张拉变径步行轮具备良好的柔性，我们使用Kistler测力传感器对张拉变径步行轮进行了弹性测试实验。将处于极限展开状态下的张拉变径步行轮在高度为250 mm的位置坠落在测力传感器上，得到张拉变径步行轮的受力曲线，如图10所示。由于张拉变径步行轮为阵列结构，故本实验仅考虑一个张拉单元的运动周期。表3为不同时间下张拉变径步行轮的受力情况。从图10中的受力曲线可以得出，张拉变径步行轮具备一定柔性且拥有一定的减振能力。

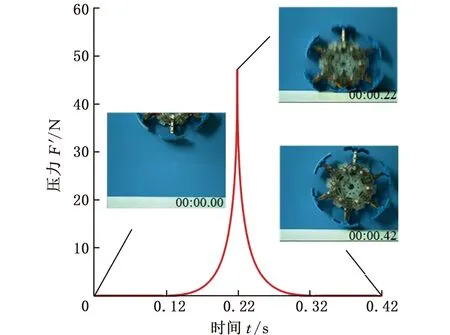
图10 张拉变径步行轮受力曲线Fig.10 The force curve of tensegrity variable-diameterwalking wheel

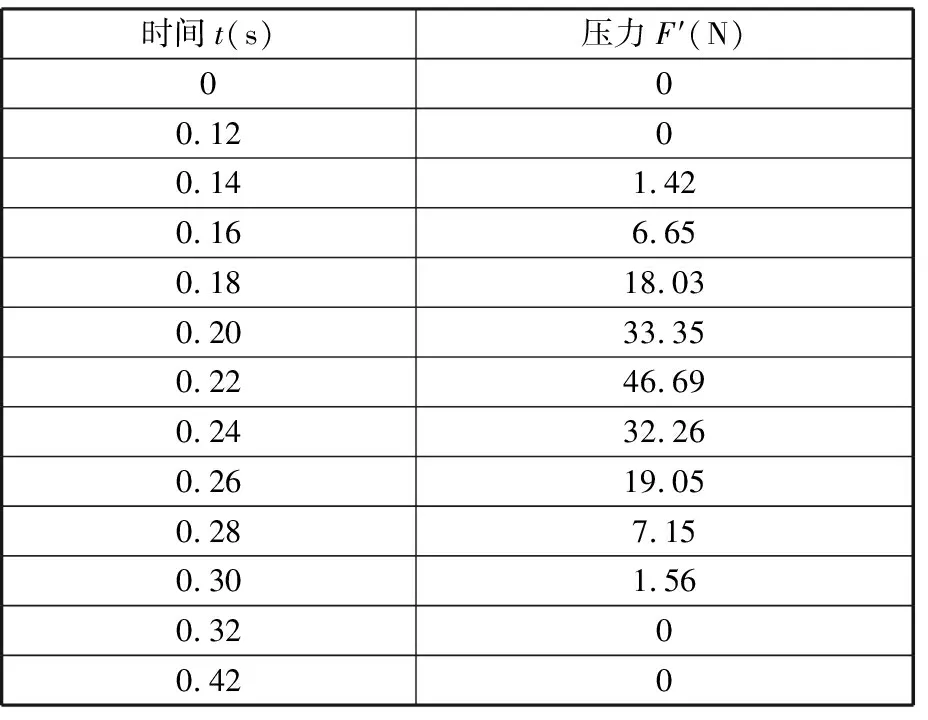
表3 不同时间下张拉变径步行轮的受力情况

5 结论

本文基于两杆三索平面张拉整体结构提出一种新型张拉变径步行单元，设计出一种轮腿式张拉变径步行轮。张拉变径步行轮具有张拉整体结构刚度大、柔顺性好、自适应性强的优点，同时具备较大的变径与抗冲击能力，并且机械结构相对简单。

与传统机器人对比，张拉变径步行轮所组成的车辆可以根据地面条件改变其功能模式，从轮式结构到腿式结构相互转换，既可以作为四轮驱动车辆(轮式模式)，又可以作为足类动物(腿式模式)，从而适应不用地形条件，且可通过主动改变车轮径向高度来实现在多地形上的稳定移动，其车轮的展收比可以达到1.427。

实验表明，张拉变径步行轮表现出在结构化地形和非结构化地形上前进、转弯、自适应的能力，并且可在车辆前后轴间距为400 mm的条件下以整体保持水平的状态爬上角度约为4°的斜坡。张拉整体结构拓宽了轮式行走机构自适应行走的研究。