高中数学课堂教学中落实直观想象素养培养的设计
2022-10-31 14:33:14201600上海市松江一中曹素玲
中学数学杂志 2022年9期
201600 上海市松江一中 曹素玲
伴随着新一轮课程改革的推进及新教材的实施,如何落实数学核心素养,提高课堂教学效率成为广大教师面临和亟需解决的问题.
与此同时,课堂教学作为落实教育教学的“主战场”,便自然而然地成为培养学生核心素养的主要阵地.
直观想象素养作为数学六大核心素养之一,是学生数学学习过程中必不可少的一种基本素养,它是指借助几何直观和空间想象感知事物的形态与变化,利用空间形式特别是图形理解和解决数学问题的素养.
笔者结合具体实例,阐述直观想象素养在高中数学课堂教学中的培养.
一、 注重教学情境的创设,激发学生学习的兴趣
在教学中要合理创设直观情境,其中包括实际情境、科学情境、数学情境、历史情境等.
合理创设情境便于学生理解学习内容和要完成的任务,能够激发学生的兴趣和热情,也有利于提高学生应用数学的能力.
例如,对于“函数的单调性”一节的引入环节进行如下设计.
情境1
回顾我们之前学习过的指数函数与对数函数的图像,分别说说当a
>1和0<a
<1时,图像所表现出的趋势如何?指数函数图像如表1所示.
表1
y=axa>10<a<1图像
对数函数图像如表2所示.
表2
y=logaxa>10<a<1图像
设计意图:
新教材对函数的编排做了很大的调整,将指数函数和对数函数提到函数的概念之前,体现了由特殊到一般的思想,顺应学生的认知发展规律,便于学生由具体函数直观地认识函数的性质.
本节课从学生熟悉的指数函数、对数函数图像入手创设情境,让学生直观感受图像中“当a
>1时,y
随x
的增大而增大”和“当0<a
<1时,y
随x
的增大而减小”的趋势,在感知函数值增减变化的过程中,推动学生对单调性由形到数的认识,将感性认识升华为理性认识.
情境2
气温曲线你注意过一天之内的气温变化吗?请根据我市某日气温随时间变化的曲线图(如图1所示),说说气温的变化情况.
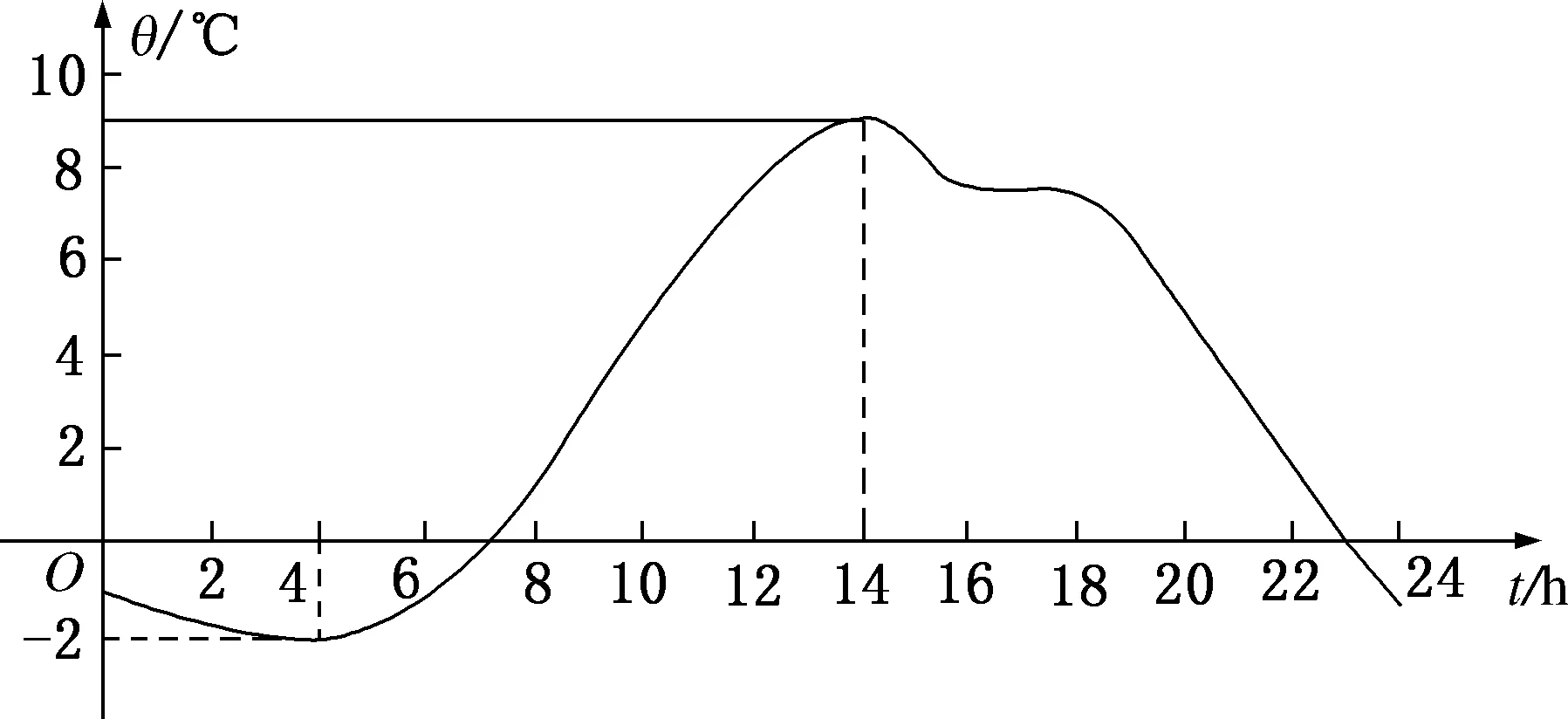
图1
设计意图:
气温波动是学生在现实生活中能够切实感受到的,借助学生实际生活的感受经验引入,让学生感受气温在某个时间段“上升”“下降”的趋势与图像单调性的联系,初步获得对函数单调性的感性认识,为理性概念的生成做铺垫.
理解函数单调性的形式定义仅仅是理解函数性质的一部分,在教学中,教师也要培养学生的模型意识,使学生在头脑中“留住”一批具体的函数模型,这样不仅可以帮助学生提升直观想象素养,还可以对辅助函数性质的教学起到事半功倍的效果.
二、 注重实物模型的制作,增进直观想象素养的发展
从平面几何过渡到立体几何时,思维方式会发生较大的变化.
从以往学生的数学学习经验来看,很多学生不具备从二维空间迅速切换到三维空间的能力,尤其对于空间想象能力欠发达的学生来说,他们遇到的困难更大.
因此,教师在进行立体几何教学时,可引导学生亲手制作立体几何模型,通过观察现实模型,恰当运用类比思想,不断培养、发展和完善学生的直观素养.
例如,让学生动手制作圆锥模型,观察从圆锥侧面沿母线剪开得到的展开图是扇形,在此基础上,教师再启发引导学生寻找平面几何与立体几何之间的关系,发现扇形弧长与底面圆周长相等,从而掌握二者间的转化.
除了制作模型,教师还要引导学生通过对模型的理解与洞察将问题直观化.
例如,在讲解“多面体的表面积”时,笔者布置了一道2005年的高考题作为拓展题.
有两个相同的直三棱柱,高为底面三角形的三边长分别为3a
,4a
,5a
(a
>0),请同学们动手制作模型并解决以下问题.
(1)用它们能拼成什么样的几何体?
(2)在所有可能拼成的直四棱柱情形中,全面积最小的是哪一个?全面积是多少?
(3)在所有的情形中,全面积最小的是一个四棱柱,求a
的取值范围.
设计意图:
模型是想象的基础,通过利用模型,学生可以更容易地理解和推理数学问题,本题主要考查棱柱的侧面积和表面积,学生通过动手制作模型,拼接模型,很快就会发现这两个直三棱柱可以拼成一个直三棱柱和三个直四棱柱,接着根据公式分别求出棱柱的侧面积和表面积,通过比较,问题就迎刃而解了.
空间想象能力的培养不是一蹴而就的,在学习立体几何之初,教师一定要多注重实物模型演示,让学生多运用直观感知、操作确认、度量计算等认识和探索空间图形的性质,逐步发展空间想象能力,培养直观想象素养.
三、 注重多媒体技术的运用,促进直观表象能力的形成
多媒体在新课程改革的背景之下担当着重要的角色,在教学过程中有着不可替代的作用.
由于信息技术具有较强的直观性,可以将静态的数学课堂转化为动态的数学课堂,在很短的时间内吸引学生的眼球,所以,在教学过程中应当注重相关教学软件的应用.
在研究A
,ω
,φ
对函数y
=A
sin(ωx
+φ
)的影响时,可以先给ω
赋值,然后通过对比各个图像之间的差异,利用几何直观感受参数ω
对函数的影响.
例如,通过作出函数y
=2sinx
和及y
=sin2x
和的图像,发现其与函数y
=sinx
图像的区别和联系.
在此基础上,通过对图像的观察,结合函数表达式进一步讨论、抽象、归纳出参数A
,ω
对函数图像及周期的影响,利用同样的方法可以探究φ
对函数的影响,最后得出结论.
(如图2所示)图2
又如,在讲解由函数y
=sinx
的图像经过怎样的变换得到的图像时,两种方法的分解图分别如图3-1、图3-2所示.
方法1:
先伸缩后平移(如图3-1所示).
方法2:
先平移后伸缩(如图3-2所示).

图3-1
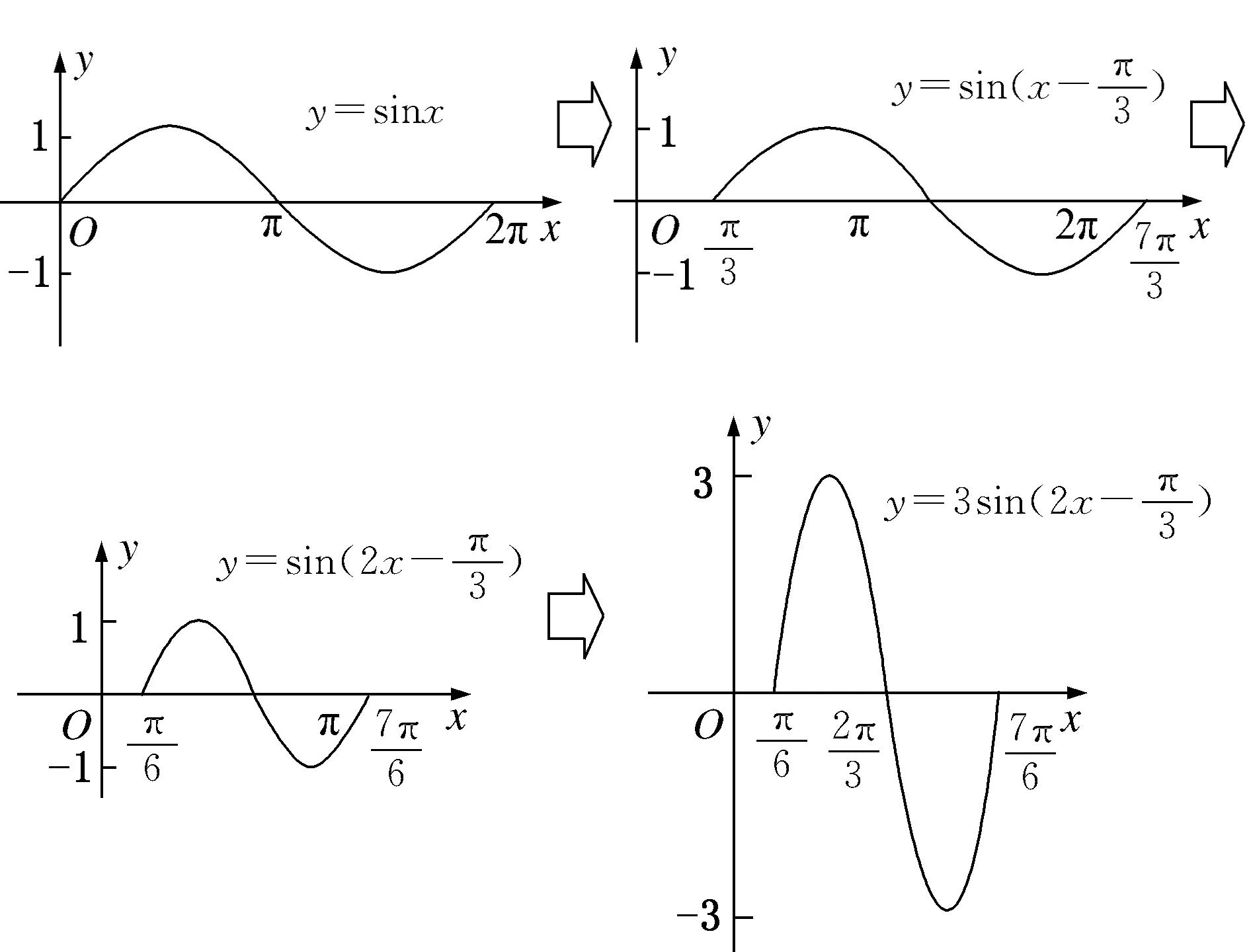
图3-2
设计意图:
函数y
=A
sin(ωx
+φ
)的图像与性质是三角函数中的一个较为抽象的内容,在较为抽象的数学知识的教学过程中,应该充分利用多媒体技术,形象地揭示知识的产生或变化过程,在动态的分析探究中深化对概念的认知,促进学生直观表象能力的形成.
四、 注重数形结合的渗透,促进直观素养的提升
直观想象是学生发现和提出数学问题,分析和解决数学问题的重要手段,是探索和形成论证思路、进行逻辑推理、构建抽象结构的思维基础.
直观想象素养的培养不是一朝一夕能够完成的,它需要教师在教学过程中不断引导学生深入挖掘题目的条件,发现条件背后隐藏的数学思想方法,并尽可能帮助学生形成一些有用的“数学模型”.
学生遇到新问题时,能对问题直观地进行判断,甚至无需论证推理就能直接看出一些结论,然后再运用相关结论解决问题.
笔者在向量的习题课中选取了这样一道例题.
在△ABC
中,若为BC
边的三等分点,则________.
向量是数学中“形”与“数”的统一,它不仅具有几何的“形”,还有“数”的特点.向量的“形”不仅是学生理解概念的一种直观的方法,也可以为学生提供解决问题的思路.
本题看似考查向量数量积的运算,而实质考查向量的“距离”.
在解决问题之前,学生需要明确两点.
(1)对于有公共始点的两向量的和与差的模分别表示相应平行四边形的两对角线长,对角线长相等的平行四边形一定是矩形.
(2)有公共点的两向量的和的模即为△AEF
第三边EF
对应的中线长AG
的两倍.
教材只讲解了向量的几何表示、三角形法则、四边形法则等,它让向量具备了“形”的特征,但对于条件表示矩形,△AEF
中的和的模为第三边EF
对应的中线长AG
的两倍,则属于需要学生积累的基本模型.
明确这两点之后就可以画出图形了(如图4所示).

图4
解答:
由知AB
⊥AC
,由AB
=2,AC
=1得因为E
,F
为BC
边的三等分点,取EF
的中点G
,则在△AEF
中,由可得故设计意图:
知识的积累依赖于直观,数形结合思想正是数学核心素养中“直观想象”的体现.
在处理本题时,正因为抓住了“公共始点”“和”“差”“模”“数量积”等关键词,把向量问题转化成三角形或四边形中的“距离”问题,才达到了数形转化的目的.
在教学中,要增强学生运用“直观想象”思考问题的意识,提高学生数学素养.
直观想象素养的培养不是在短时间内就能完成的,它需要依托具体的数学知识与方法,在数学知识的学习、数学思想方法的掌握过程中,通过逐步积累、领悟、内省形成.
对于绝大多数学生来说,数学能力的形成与数学核心素养的提升主要依赖于(或源于)数学课堂,因此,在结合新教材备课的过程中,教师要多思考教材编写者的意图是什么,教师应该向学生教什么,怎么教,这样才能使直观想象素养的培养得到有效体现与落实.
猜你喜欢
新高考·高一数学(2022年3期)2022-04-28 07:02:46
科普童话·学霸日记(2021年4期)2021-09-05 04:28:51
中学生数理化(高中版.高考数学)(2021年1期)2021-03-19 08:28:36
中学生数理化·中考版(2020年12期)2021-01-18 06:59:40
小学生作文(低年级适用)(2019年12期)2020-01-18 07:50:36
新高考·高二数学(2019年2期)2019-09-05 11:15:09
中国化妆品(2018年6期)2018-07-09 03:12:42
小学生学习指导(低年级)(2018年6期)2018-05-25 01:42:26
读者(2017年15期)2017-07-14 19:59:34
高中生学习·高三版(2016年9期)2016-05-14 09:12:05

