滑枕模态试验与分析

赵彦鹏， 杨 军， 廖广宇， 王 丹， 韩玉稳

（云南省机械研究设计院有限公司/云南省机电一体化应用技术重点实验室， 云南 昆明 650031）

0 引言

数控机床在工作环境下， 动态激振力会使结构产生动态位移，而且会导致结构的疲劳甚至损坏，所以仅凭静态设计很难满足机床对于动态性能的要求， 机床的动态特性是影响其精度保持性和可靠性的关键因素。 滑枕是数控机床重要功能部件， 直接承载着受切削力影响产生的动态载荷。 滑枕在动态载荷下的振动量级、固有频率、刚度等这些结构特性是结构的固有属性， 也就是结构的模态参数。通过模态分析获得结构的模态参数，为结构的设计优化提供依据。

1 模态试验设计

1.1 试验对象

试验对象为龙门数控铣床的滑枕部件，由HT300 铸造而成。 主轴系统的电机、铣头、变速机构等安装在滑枕部件上， 电机功率最大22kW， 主轴设计最高转速为4000r/min，刀柄为BT50 规格，滑枕通过导轨副与滑座相连做Z 向运动，行程为800mm，见图1。

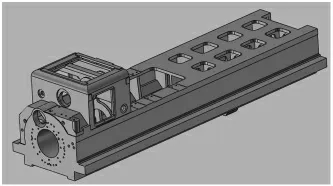
图1 滑枕

1.2 试验内容和目的

以滑枕为研究目标，综合应用试验模态测试技术、试验模态分析技术等开展相关试验测试；形成滑枕的动态特性试验分析方法，获得结构的模态参数，为结构的设计优化提供依据，为产品动态性能提升提供实现路径。

1.3 试验原理

模态分析是一种分析方法， 运用动力学属性描述结构的特性， 动力学属性包括结构的固有频率、 阻尼和振型。 从数学意义上定义是指将线性定常系统振动微分方程组中的物理坐标变换为模态坐标， 对方程解耦使之成为一组以模态坐标及模态参数描述的独立方程， 以便求出系统的模态参数。 坐标变换的变换矩阵为模态矩阵，其每列为模态振型。 因此，模态变换是将方程从物理空间通过模态变换方程变换到模态空间的过程； 是将一组复杂的、耦合的物理方程变换成一组单自由度系统的、解耦方程的过程。 简单的说就是通过激励装置对结构进行激励，在激励的同时测量结构响应的一种测试分析方法，见图2。

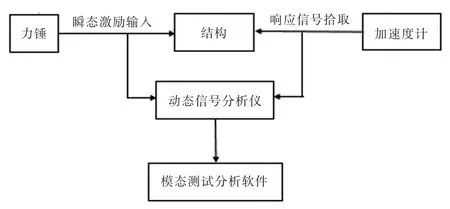
图2 试验模态测试原理图

1.4 试验设备

试验采用B&K8207 力锤进行激振，力锤频率范围0～1000Hz，灵敏度0.225mV/N，最大激励力5000N；B&K4506B三向加速度传感器获得响应信号，传感器频率范围：0.6～3000Hz，灵敏度为100mV/g，测量范围（峰值）70g，最大冲击（峰值）5000g；使用B&K 3660C 数据采集前端与B&K基本分析系统以及PULSE Reflex 高级模态采集与分析包，构成试验测试分析系统。

2 模态试验测试技术

2.1 确定边界条件

试验模态测试时， 试件应尽可能的接近实际工作状态的边界条件。但现实中由于某些零部件可能在实际边界条件下无法进行测量，或者基于其他一些原因，工程上很多时候在自由边界条件下进行测试。本次测试采用软绳吊装，将滑枕悬空吊装模拟其自由边界进行试验，见图3。

图3 模拟滑枕自由边界条件

2.2 确定激励方式

对于EMA 试验而言，激励方式分锤击法和激振器法。 本试验使用锤击法，激励点为滑枕导轨靠主轴端的X向、Y 向、Z 向， 测量方式为固定参考点，移动传感器方法。

锤击法由于力锤移动方便，不影响试件的动态特性，通常适用于简单的线性结构（部件级），不适用于非线性结构。 激振器测试激励能量更大，分布更均匀，获得的数据质量更高，所以，通常用于大型复杂结构，且是研究非线性的唯一方法。 但是激振器难于安装，操作复杂，存在附加质量影响。力锤作为激励设备，设备简单，投资小。相对激振器而言，力锤移动方便、不影响被测结构的动态特性，因而适用于快速地进行结构测试。

2.3 确定传感器类型、安装方式

传感器的可靠性、 精确度等参数直接影响到系统的质量。传感器的选用原则如下：①灵敏度；②响应特性；③线性范围；④其它因素。

2.4 确定测量自由度

机床部件运动时， 用以完全确定结构在空间上的位置所需的最少独立坐标个数，称为自由度。例如描述可在空间任意运动的一个质点的位置需3 个独立坐标， 则其自由度为3，若限制质点在某曲面或某曲线上运动，则其自由度减为2 或1。 又如自由运动的刚体有6 个自由度，即3 个平动自由度和3 个转动自由度。 三个平动自由度确定质量中心的位置，三个转动自由度确定刚体的方位。

本试验整个滑枕共布置380 个测点， 响应自由度为380×3=1140。 激励点依据工程经验选择在滑枕导轨靠主轴端，数量为1 个，激励自由度为3 个正交方向，总FRF=1140×3=3420，见图4。

2.5 生成几何模型

几何模型由点、线或面构成，而模型中的点用于表征实际的测量位置。最终生成的几何模型就是由这些实际的测点位置的坐标表示，由点到线、由线到面。 所以试验模态的几何模型是由实际测点位置表示的线框模型，而非实体模型。 用于表征模型动画， 通过后续的振型动画， 可以确定各阶模态的节点位置， 见图5。

图5 几何模型

2.6 数据采集

确定所使用的各设备都能正常工作和对测量系统进行校准。 这一步又分为预采集和正式采集。 预采集是为了确定合理的参数， 包括采样频率、采集仪量程设置、采样时长、锤击法需要确定触发、确定参考点位置等。 另一方面还需要对数据进行检查，包括线性检查、FRF 和相干检查、互易性检查等。

本试验分析带宽设为1.6kHz，谱线数设为1600，频率分辨率为1Hz，平均方式为线性平均，平均次数为5 次；激振力大小为1.0kN～1.5kN；对力锤脉冲信号使用Hanning窗函数，对响应瞬态信号使用Exponential 窗函数；滤波器设为7Hz 高通滤波，FRF 为自动量程采集，见图6。

图6 数据采集

3 模态试验分析技术

3.1 模态数据选择

依据测试过程中模态参考点的数量， 选择数据时可以按单参考点数据或多参考点数据来进行分析。 即使测试过程中使用了多个参考点， 但如果选择模态分析数据时，只选择其中的一列，那么最终分析时，也是按单参考点来分析的。选择多参考点数据，可最大限度地提取到所有关心的模态，丢失模态的可能性最小。 因此，如果是多参考点模态数据，优先选择所有的参考点数据，除非某个参考点数据质量太差， 才不选择它。 本试验采用多参考点，激励信号双向同时参与分析计算，见图7。

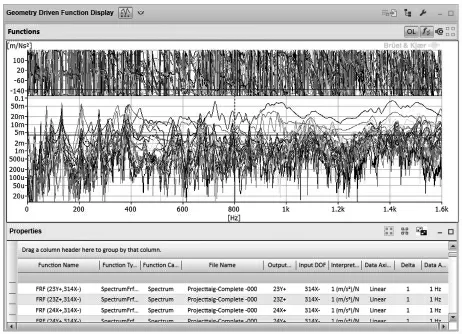
图7 频响函数（ALL FRF）参与计算

3.2 确定分析带宽

测量得到的FRF 包含多个共振峰，如图7 所示的共振峰，这些共振峰可能相隔较近，也可能相隔甚远，如模态密度大，那么共振峰之间相隔必然较近。相隔较近的各阶模态必然相互影响较严重， 而相隔较远的模态相互之间的影响较轻。在确定分析频带时，必然存在带内与带外的区域。带内是指要进行模态分析的频带，而带外则是分析频带之外的频带。为了减少带外对分析频带内的影响，确定的分析频带的边界应位于反共振峰位置处， 如果选择的FRF 不存在反共振峰，如跨点FRF 或SUM 函数，那么，选择的分析频带边界应位于幅值最小的频率处。

3.3 模态参数提取

（1）确定系统极点。确定系统极点通常是通过稳态图来获得，见图8。 因而，在确定系统极点时，有两个关键的因素需要确定：第一个是Modal size 多大合适；第二个是选择极点时，选择哪个位置点更合适。

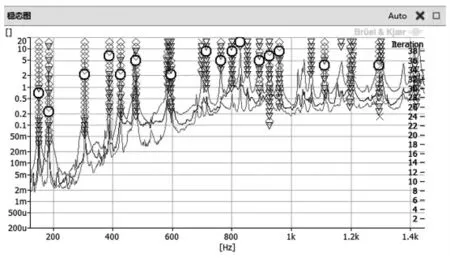
图8 稳态图

（2）确定模态振型。 这一步必须要包括所有测点的FRF，因为振型是局部特性，跟测点位置有关。如果不包括所有测点的FRF，则计算不出相应测点的振型值，在振型动画中该测点即为不动点，但又不是节点，而是因为没有计算这一测点的振型值导致的。

本试验采用多参考最小二乘复频域法结合复模态指数函数（CMIF）和稳态图识别模态参数。

3.4 结果验证

对得到的模态结果进行验证， 验证的目的是对模态参数估计结果的正确性进行检验。有经验的工程师凭借经验在一定程度上也可以做判断。当然，除了经验判断之外，我们还有许多手段。 模态验证可以按照三种级别进行。

第一级验证相当直观，不涉及任何数学工具。对振型进行视觉检查（这时经验就显得尤为重要了），或者把实测得到的频响函数与从模态参数识别过程中综合得出的频响函数进行比较， 这些都是这一级模态模型验证的典型方法。

图9 MAC（模态置信准则）值

第二级验证是利用某些数学工具来检验估计出来的模型质量。 比如模态判定准则（MAC），模态参与（MP），互易性，模态超复杂性，模态相位共线性，平均相位偏移，模态置信因子（MCF）等。

第三级验证是工具验证： 可以使用计算模型对试验模型进行验证，如相关性分析。

3.5 试验结果

模态振型描述：1 阶振型： 图10 为该滑枕第1 阶模态振型，部件沿Z 轴，作1 次左右扭摆动作；2 阶振型：图11 为该滑枕第2 阶模态振型， 部件绕X 轴作1 次上下弯曲动作；3 阶振型：图12 为该滑枕第3 阶模态振型，部件绕Y 轴作1 次左右弯曲动作；4 阶振型：图13 为该滑枕第4 阶模态振型，部件绕X 轴作2 次上下弯曲动作，箱体的顶部变形较大；5 阶振型： 图14 为该滑枕第5 阶模态振型，部件绕Z 轴作2 次左右扭摆动作；6 阶振型：图15 为该滑枕第6 阶模态振型，部件头部绕Z 轴作左右弯曲，部件尾部沿Y 轴作上下扭摆。

图10 1st Mode：151.32Hz

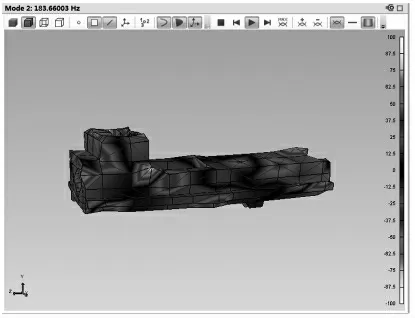
图11 2st Mode：183.66Hz

图14 5st Mode：425.21Hz

试验结果见表1。

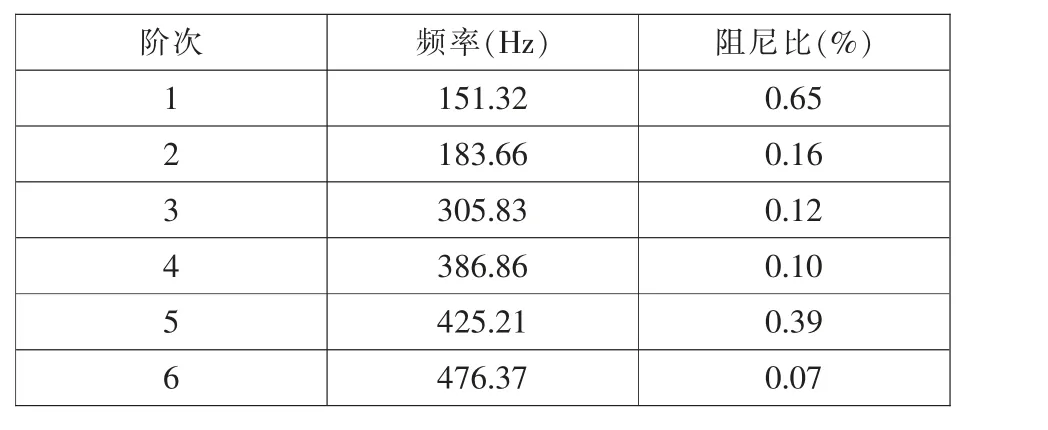
表1 试验结果

3.6 试验结果分析

从图10～图15 中各阶模态振型进行分析： 滑枕总体设计良好，质量与刚度匹配较好，振型平滑；主轴变速箱体部分采用四边形结构， 在箱体顶部和箱体内部主传动齿轮的轴承座板处存在局部弯曲和扭摆， 振幅较大。

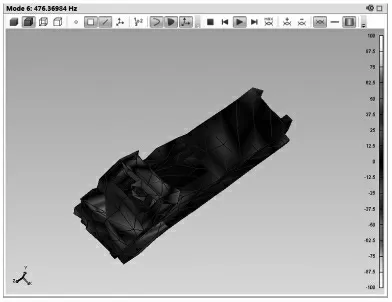
图15 6st Mode：476.37Hz

4 建议

滑枕的主轴变速箱体部分结构薄弱，整体刚度偏低；箱体中间的轴承孔座连板刚度不足， 可以通过增加四周壁厚， 轴承座板处如果空间允许可以增加筋条， 提高四方体顶端和轴承座板的抗弯曲和扭转能力。

5 结束语

本试验介绍了滑枕部件试验模态测试与分析的方法， 通过试验模态测试与分析， 获得了滑枕结构的特征参数， 进行了结构分析并提出了改进意见， 为结构系统的振动特性分析和结构动态特性的优化提供依据。