基于串联电阻估计的光伏阵列热斑故障诊断方法

王方政，刘喜泉，陈浈斐，喻洋，晏璐

（1.中国长江三峡集团有限公司科学技术研究院，北京 100038；2.河海大学能源与电气学院，江苏南京 211100）

0 引言

随着绿色能源的推广，太阳能发电技术发展迅速[1-2]。太阳能发电技术的物理原理就是利用光生伏特效应，将照射到光伏面板的太阳能转化为直流电能，再通过电力电子器件转化为各种类型的电能供负载使用[3-5]。在太阳能发电的过程中，光伏电池是发电过程中的核心组件。但是由于生产、运输和环境因素的影响，光伏面板的故障频发，例如隐裂、划伤、积灰和热斑效应频繁发生[6-9]，这不仅使得光伏面板的输出效率降低，寿命减短；严重时甚至可能引发火灾，威胁到光伏电站的运行、使用[10-14]。

由美国国家可再生能源实验室组织的国际光伏质量保证特别行动组研究表明，在这些实际运行光伏电站的典型热斑问题中，有3 类比较常见[15]，即电池间显著温差、单串电池性能失效、玻璃与电池碎裂。由玻璃与电池碎裂可能引起的反偏漏电流或反偏电压，将导致光伏组件在局部温度极速上升，电池和面板在短时间内可能直接烧毁。

热斑故障引起了许多国内外许多专家的关注及研究[16-18]。为了深入研究光伏热斑失效问题，文献[19]提出了对光伏电池的输出特性曲线利用平抛运动公式满足工程需求，同时，可以极大减少运算量；文献[20-21]在考虑反向雪崩效应下，对不同阴影条件下建立了光伏模组数学模型和Saber 仿真模型，分析了局部阴影条件下光伏模组的I-U和P-U特性及输出能力变化；文献[22-23]对产生热斑效应的光伏组件进行分析，通过分析采用旁路二极管对智能接线盒进行预测，模拟不同反向漏电流。对于阴影遮挡面积与反向电流的相关性，文献[24]中提出了新型诊断方法，根据光伏阵列的等效计算模型，计算出组件的等效串联电阻，进而通过参数比较法判定其运行状态，确定光伏阵列是否发生故障；文献[25-26]中提出了一种基于模糊控制的热斑故障诊断及优化控制策略，对光伏组件输出特性进行扫描；文献[27]中分析了光伏面板中扰动观察法对于追踪最大功率点的有效性。综上所述，在光伏阵列中导致其产生热斑故障的原因在于被遮挡的光伏电池中的电流失配。

针对光伏面板由于电流失配所导致的热斑故障，提出了一种在线诊断热斑效应的故障诊断方法，该方法将传统的电压、电流检测方法、时间跟踪法和参数估算模型相结合，准确定位故障电池模块；最后，通过仿真软件分别对单个光伏电池和串并联（Series-Parallel，SP）结构的光伏阵列进行建模，分析热斑故障对光伏阵列输出特性的影响。

1 光伏阵列数学模型

太阳能光伏（Photovoltaic，PV）发电是一种极具有潜力的清洁能源。光伏电池是一种将光能转换成电能的半导体元件，其工作原理是光生伏特效应，即被太阳光照射到的半导体产生电动势。光伏面板则是由若干个光伏电池模块串、并联组合、封装而成，其核心是光伏电池模块。光伏电池模块由P 型和N 型半导体组成，其中两种半导体中间的连接处称为PN 结。

1.1 单个光伏电池数学模型

假设太阳光照强度不变，处于该状态下的光伏电池生成的光生电流保持不变，在等效电路模型中相当于恒流源[28]，光伏电池单二极管等效电路模型如图1 所示。

图1 光伏电池单二极管模型Fig.1 Single diode model of photovoltaic cell

图1 中，Id为光生电流Iph经过负载偏置于PN结生成的暗电流；Ibr为反向雪崩击穿电流；Ish为流经并联电阻的电流；Rs，Rsh分别为光伏电池的等效串、并联电阻；U，I分别为光伏电池输出电压和输出电流。

在光伏电池模块中，考虑了二极管的反向雪崩击穿效应，由等效电路模型可得单个光伏电池的输出特性为：

式中：Io为等效二极管的反向饱和电流；Ior为在标准环境（1 000 W/m2，25 ℃）下等效二极管的反向饱和电流；a，b为雪崩击穿特征常数；Ubr为雪崩击穿电压；q为电子电荷量；Ego为半导体带隙能；A为二极管的理想因子；B为曲线拟合常数；k为玻尔兹曼常数；T为电池热力学温度；Tr为标准温度取25 ℃；S为实际光照强强度；Sr为标准光照强度1 000 W/m2；Isc为短路电流；KI为短路电流温度系数。

1.2 光伏阵列数学模型

大量的光伏电池元件通过串、并联的方式，封装为一个整体，即为光伏阵列。图2 给出了m×n（m个n条）串联支路并联形成的SP 光伏阵列结构和等效电路模型。图2 中，Uout和Iout分别为光伏阵列总的输出电压和输出电流。

如图2 所示，假设光伏阵列中各个光伏电池元件均为理想电气元件，电气参数完全相同时，光伏阵列的数学模型为：

图2 m×n光伏阵列模型Fig.2 Models of m×n photovoltaic array

2 光伏电池热斑故障分析

2.1 热斑故障产生机理

通常忽略电池参数原因，在局部阴影产生的电流失配的情况下，光伏阵列的输出功率具有多峰[29-30]。当光伏电池模块受到局部阴影的影响出现电流失配时，由于被遮蔽的光伏电池产生的光生电流小于串联组件中其他光伏电池产生的光生电流，其两端将会产生反向电压，图3 给出了被遮蔽光伏电池的反偏等效电路模型。图3 中，UR为光伏电池外部负载两端电压；Irev为光伏电池漏电流。

图3 光伏电池反偏等效电路模型Fig.3 Reverse bias equivalent circuit model of photovoltaic cell

根据基尔霍夫电流与电压定律，当电路的电流比被遮挡单体光伏电池所能提供的最大电流（即短路电流）还要大时，该单体光伏电池只能取负压，即漏电压。

在漏电压的作用下，光伏电池将产生与光生电流同方向的漏电流，当漏电流长时间出现时，可能会导致光伏面板产生热斑故障。当电池通过串接或者并接连接在一起时，如果每一块电池的输出功率不一样，功率较低的电池就会消耗其余电池的功率，导致整体输出功率的下降，也就是说一个光伏组件能输出多少功率是由输出功率最低的电池决定的。

由图3 可知，被阴影遮挡的电池所消耗的功率Pd为：

由式（8）可知，漏电流Irev越大，光伏电池因故障消耗的功率也就越大，产生的热量也就越多。

被遮挡的电池阵列的温升来源于吸收太阳光的能量和被遮挡位置的电消耗传递给遮挡物的热量[31]，假设被遮挡电池所产生热量没有损失也没有向周围耗散，全部被遮挡物所吸收，则光伏电池的温升ΔT可表示为：

式中：α，β为遮阴材料光能转化为热能的系数、热传递系数；θ为功率衰减转换为热能的比例；Qp为光能；P0，P1为无遮挡的输出功率和有遮挡情况下的输出功率。

式中：κ为常数。

通常Rsh＞＞Rs（多晶体硅光伏电池Rsh为100～200 Ω；Rs为0.002～0.003 Ω），因此忽略等效串联电阻消耗的热量，从而得到：

从式（11）可以看出，随着反向漏电流增大，被遮挡处光伏电池温度上升，引发热斑效应。

2.2 防止热斑效应的措施

为防止光伏电池阵列由于热斑效应，部分电池成为负载发热导致模组损坏，最好在太阳电池组件的正负极之间并联一个旁路二极管，以提高光伏阵列在局部阴影下的输出能力，同时避免光照组件所产生的能量被受遮蔽的组件所消耗[32-33]。

此时，若某一光伏电池因存在热斑故障而无法输出功率，旁路二极管会使得其它正常的光伏电池组件产生的光生电流从该二极管通过，避免由于其中一个或者几个电池存在故障而使整个光伏面板停止工作。旁路二极管的连接方式如图4 所示。

图4 考虑旁路二极管的光伏阵列模型Fig.4 Photovoltaic array model considering bypass diode

当光伏面板被阴影遮挡时，光伏面板此时可能存在2 种工作方式：

1）光伏组件正常输出的电流I小于或等于故障单个光伏电池所产生的最大光生电流时，即，此时光伏电池被遮挡程度较为轻微，因此不会产生漏电流；

2）光伏组件正常输出的电流I大于故障单个光伏电池所产生的最大光生电流时，即，此时光伏电池被遮挡程度较为严重，此时就会出现较大的漏电流。

此时，故障光伏电池两端带有负压且随其增大至旁路二极管导通电压时，旁路二极管导通，将故障光伏电池短路，减小故障电池负压以及漏电流，避免光伏电池短时间过热引起安全事故。

3 光伏阵列故障诊断方法

考虑到光伏面板由多组光伏电池串并联组成，一旦发生热斑故障，难以对故障电池进行定位和故障程度的判断，因此基于式（7）中的光伏阵列数学模型提出了一种光伏阵列的热斑故障诊断方法，具体诊断流程如图5 所示。图5 中，Uj为光伏阵列中第j列电池串两端电压的采集值，Umin为所有电池串电压采集值中的最小值，ΔUj为二者之差。

图5 光伏阵列故障诊断流程Fig.5 Fault diagnosis process of photovoltaic array

该方法通过将传统的电压、电流定位法、时间跟踪描述和光伏电池参数估算模型相结合，准确判别故障类型，定位故障发生的位置，最终定位故障电池。

3.1 电压、电流定位法

对于m×n的SP 结构光伏阵列，在正常情况下，每个电池串上m个电池组件流过的电流是相等的，即为：

式中：i为串联电池的行号，1 ≤i≤m；j为并联电池串的列号，1 ≤j≤n。

当光伏阵列发生故障时，其输出电流和输出电压必定产生变化。假设在第h行第l列的电池发生故障（1 ≤h≤m；1 ≤l≤n）时，则有：

式中，i≠h。

当第l列有光伏电池出现故障时，该列的电压即会产生下降，则总输出电压也会产生下降。

式中：Ui为电池串中第i个电池的输出电压。

根据光伏电池的伏安特性曲线，除第l列外的其他并联支路输出电流Iij将会上升。此时，发生故障的电池串输出电压和电流就小于其他电池串，此时即可定位故障的电池串。

3.2 时间跟踪法

由于热斑现象可分为3 部分：一部分为阴天、树叶、云层的移动等环境变化所造成的光伏电池短期电流失配；另一部分为电池隐裂、断栅造成的长时间微小的电流失配问题；还有一部分为污垢所带来的长期的严重的遮挡问题。为了辨别不同因素带来的故障判别的困扰，可以采取时间跟踪法的方式来判断故障发生的程度，每隔2 h 对采集的电池串的电压、电流值进行判断，若连续3 次判断为故障电池串，则可以将其确定为故障电池串。

3.3 光伏电池参数估算模型

对于电压、电流定位法和时间跟踪法而言，可以大致定位组件故障发生的位置，但对于特定的故障电池仍难以定位。因此，结合光伏电池的参数估算模型是有必要的。除此以外，参数的估算可以在线检测，避免了由于故障诊断带来的光伏电池组的停运。根据式（1）—式（6）中光伏电池等效模型，忽略反向雪崩效应，可得单个光伏电池的电流方程为：

当光伏组件短路时，短路电流为Isc。代入U=0，I=Isc，此时流过等效二极管的电流Io≈0，可以忽略，由式（15）可得，短路电流Isc可近似简化为：

当组件开路时，开路电压为Uoc。代入I=0，U=Uoc，由式（15）可得：

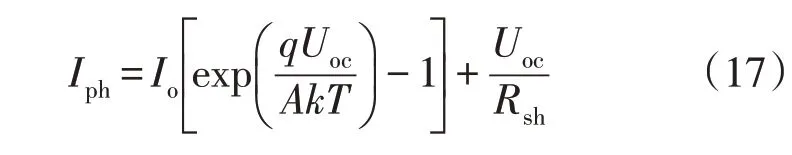
当光伏组件输出最大功率Pm时，记其电流为Im，电压为Um；代入I=Im，U=Um，则式（15）可化为：

根据(dU/dI)|P=Pm=-Um/Im，在光伏位于最大功率点处对式（18）求导，可得：

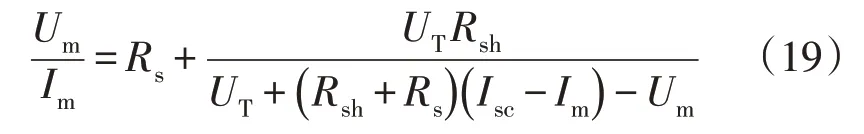
式中：UT为热电压，其表达式为：

根据在标准温度下，二极管反向饱和电流的计算公式为：

式中：Iscr为在标准条件下的短路电流；Uocr为在标准条件下的开路电压。

由于二极管的理想因子A反映了光伏电池内部载流子的负荷能力，不受环境参数的影响，因此可以通过2 种不同环境条件下的开路电压和短路电流值计算获得：

式中：Uoc1，Isc1为环境条件1 下的开路电压和短路电流，Uoc2，Isc2为环境条件2 下的开路电压和短路电流。

由式（15）-式（22）可计算出短路电流Isc、开路电压Uoc、最大功率点处的电流Im和电压Um。

估算串联电阻阻值时，在光伏电池处于最大功率状态下，忽略并联电阻，串联电阻的估算表达式为：

基于式（23）中的光伏电池参数估算模型，即可根据采集的光照强度和温度数据，逐一计算故障列中各光伏电池的参数。为了考虑温度变化对不同故障程度下光伏电池串联电阻估算值Rs的影响，分别对25 ℃，40 ℃，55 ℃和80 ℃4 种温度下，某光伏电池Rs值随故障程度的变化情况进行仿真计算，如图6 所示。

图6 不同温度下Rs随故障程度的变化曲线Fig.6 Variation curves of Rs with fault degrees at different temperatures

由图6 可知，随着光伏电池热斑故障程度增加，Rs明显增大。但温度上升，会使得Rs的值略有降低。因此将光伏电池不同温度下计算得到的Rs估算值与其相应温度下的正常值对比，就可判断光伏电池是否故障以及故障的严重程度。

4 光伏阵列热斑故障诊断方法验证

4.1 单个光伏电池输出特性仿真分析

为了验证所提方法的有效性，本文基于Matlab/Simulink 软件对光伏阵列进行仿真模型搭建，如图7所示。

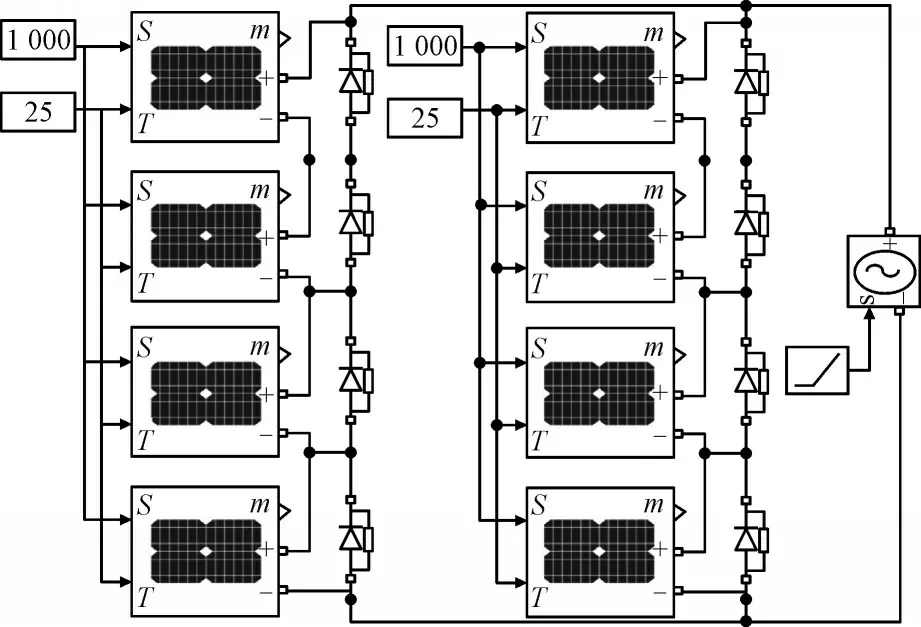
图7 光伏阵列Simulink仿真模型Fig.7 Simulink model of photovoltaic array

以1Soltech 1STH-215-P 型号的光伏电池为例。当光伏电池的温度T为25 ℃，光照强度S为1 000 W/m2时，其基本工作参数如表1 所示。

表1 1Soltech 1STH-215-P光伏电池基本参数Table 1 Basic parameters of 1Soltech 1STH-215-P photovoltaic cells

图8 给出了单个光伏电池在标准温度25 ℃下，光照强度分别为300 W/m2，500 W/m2，700 W/m2，900 W/m2，1 100 W/m2，1 300 W/m2时的输出特性。图9 给出了单个光伏电池在标准光照强度1 000 W/m2下，环境温度分别为10 ℃，20 ℃，30 ℃，40 ℃，50 ℃时的输出特性。

由图8 可知，在标准温度为25 ℃的情况下，光伏电池的最大输出功率和输出电流随着光照强度增大而增大。当光照强度由300 W/m2增加至1 300 W/m2时，输出功率由66.5 W 逐渐增大到280.5 W，输出电流也由2.36 A 增大到10.22 A。

图8 不同光照强度下单个光伏电池输出特性Fig.8 Output characteristics of single photovoltaic cell under different light intensity

由图9 可知，在标准光照强度1 000 W/m2下，当光伏电池的输出电压小于25 V 时，光伏电池的输出功率和输出电流基本不受环境温度的影响；而当输出电压超过25 V 以后，环境温度越高，则其输出功率和输出电流越小。环境温度由10 ℃升至50 ℃的时候，光伏电池的最大功率也从232.3 W 跌至197.3 W。

图9 不同温度下单个光伏电池输出特性Fig.9 Output characteristics of single photovoltaic cell at different temperatures

4.2 热斑故障下光伏阵列输出特性

在没有受到阴影的影响且忽略环境温度的影响下，每个光伏电池的输出电压和电流应该非常接近；当受到环境阴影影响时，该光伏电池由于其输出电流小于其他光伏电池的输出电流，该光伏电池被旁路二极管所短路，直致其所在的支路电流小于故障光伏电池能发出的最大电流时，该电池模块才会输出电压。此时，串联支路的输出电压可表示为：

式中：Si为串联支路中第i个光伏组件上的实际光照强度；Ui为该光伏组件的输出电压。

当Si＞Sr时，Ui值随光照强度Si变化而变化。

以4×1 光伏阵列电池串为例，假设该电池串的第1 个和第2 个光伏电池没有受到光伏电池的影响，光照强度为S1=S2=Sr，第3 个电池的光照强度为S3=0.75Sr，第4 个电池的光照强度为S4=0.5Sr，则该电池串的仿真模型如图10 所示。

图10 4×1光伏阵列仿真模型Fig.10 Simulation model of 4×1 photovoltaic array

图10 中，Is1，Is2，Is3，Is4分别为4 个光伏电池的输出电流。

当该光伏阵列中部分光伏电池被遮挡时，其输出特性分为3 个区间，如图11 所示。

1）当该4×1 光伏阵列电池串工作在区间1 时，受到阴影影响的光伏电池输出电流小于当前支路总的输出电流Iout，所以第3 个、第4 个的光伏电池均被旁路二极管短路，此时仅有第1 个和第2 个光伏电池正常工作。

2）随着光伏电池的电压的增大，其输出电流不断降低，当该光伏阵列的输出电流Iout其值降低至与第3 个故障电池所产生的输出电流Is3相等，即达到图11 中拐点1 时，此时旁路二极管D3关断。光伏阵列工作于区间2，第3 个光伏电池恢复工作，第4个光伏电池仍被旁路二极管短路。

图11 局部阴影下4×1光伏阵列输出特性Fig.11 Output characteristics of 4×1 photovoltaic array under partial shading conditions

3）随着光伏阵列电压的继续增大，其输出电流继续降低，当光伏阵列的输出电流Iout其值降低至与第4 个故障电池所产生的输出电流Is4相等，即达到图11 中拐点2 时，此时旁路二极管D4也关断，该工作于区间3 中，所有光伏电池组件均恢复到正常工作状态。

4.3 热斑故障诊断方法的准确率分析

进一步为了验证本文所提方法的准确性，分别选取2 种不同参数的光伏电池组成8×1 的光伏阵列进行故障仿真分析。首先通过设置光伏阵列中热斑故障电池的个数和故障程度模拟不同的故障情况，再计算出每种故障下的串联电阻Rs的估算值，将其与正常工况下的电阻值相比对判断光伏电池故障情况，高于正常值的视为存在故障。本文对每种光伏阵列各设置了20 组不同的情况进行仿真，其中第1 组为正常工况，其余第2—19 组均为故障工况，2 种光伏阵列在每组情况下的Rs估算值和诊断结果分别如表2 和表3 所示。

根据表2 和表3 所计算得到的40 种情况下的Rs值可知，有3 组热斑故障情况未检测出来。因此，本文所选定的对光伏电池串联电阻阻值的变化来检测热斑故障方法所存在的准确率约在92.5%左右，验证了本文所提出光伏电池故障诊断方法的有效性和准确性。

表2 光伏阵列Ⅰ在不同热斑情况下的故障诊断情况Table 2 Fault diagnosis of photovoltaic array I under different hot spot conditions

表3 光伏阵列II在不同热斑情况下的故障诊断情况Table 3 Fault diagnosis of photovoltaic array II under different hot spot conditions

5 结论

本文基于光伏电池的单二极管模型，建立了单个光伏电池和光伏阵列的数学模型。并通过将传统的电压/电流定位法、时间跟踪描述和光伏电池参数估计模型相结合，提出了一种光伏电池的故障诊断方法。最后，通过仿真平台分析了局部阴影条件下光伏阵列的I-U和P-U的输出特性的变化，研究结果表明单个光伏电池的输出功率与光照强度正相关，与环境温度负相关；部分阴影条件下光伏阵列的P-U特性曲线呈现多峰值特征，并通过仿真验证了本文所提出的光伏电池故障方法的有效性和准确性。